Hostname: page-component-7479d7b7d-8zxtt Total loading time: 0 Render date: 2024-07-13T20:14:41.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups of Wielandt length two

Published online by Cambridge University Press:  24 October 2008

Elizabeth A. Ormerod
Elizabeth A. Ormerod
Affiliation:
The Australian National University, G.P.O. Box 4, Canberra A.C.T. 2601, Australia
Get access Rights & Permissions [Opens in a new window]

Extract

The Wielandt subgroup ω(G) of a group G is the subgroup of elements that normalize every subnormal subgroup of G. This subgroup, now named for Wielandt, was introduced by him in 1958 [15]. For a finite non-trivial group the Wielandt subgroup is always a non-trivial, characteristic subgroup. Thus it is possible to define the ascending Wielandt series for a finite group G which terminates at the group. Write ω0(G) = 1, and for i ≥ 1, ωi(G)/ωi–1(G) = ω(G/ωi–1(G)). The smallest n such that ωn(G) = G is called the Wielandt length of G, and the class of groups of Wielandt length at most n is denoted by 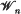. From the definition it follows that 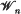is closed under homomorphic images and taking normal subgroups. Nilpotent groups in 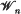are also closed under taking subgroups.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 2 , September 1991 , pp. 229 - 244
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baer, R.. Der Kern, eine charakteristiche Untergruppe. Compositio Math. 1 (1934), 254–283.Google Scholar
[2]Baer, R.. Gruppen mit Hamiltonschem Kern. Compositio Math. 2 (1935), 241–246.Google Scholar
[3]Cannon, John J.. An introduction to the group theory language, Cayley. In Computational Group Theory (Academic Press, 1984), pp. 145–183.Google Scholar
[4]Cooper, C.. Power automorphisms of a group. Math. Z. 107 (1968), 335–356.CrossRefGoogle Scholar
[5]Dedekind, R.. Über Gruppen deren sämtliche Teiler Normalteiler sind. Math. Ann. 48 (1897), 548–561.CrossRefGoogle Scholar
[6]Hall, M.. The Theory of Groups (Macmillan, 1959).Google Scholar
[7]Hobby, C.. Finite groups with normal normalizer. Canad. J. Math. 20 (1968), 1256–1260.CrossRefGoogle Scholar
[8]Hogan, G. T. and Kappe, W.. On the H p-problem for finite p-groups. Proc. Amer. Math. Soc. 20 (1969), 450–454.Google Scholar
[9]Mahdavi, S. K.. A classification of 2-generator 2-groups with many subgroups 2-subnormal. Comm. Algebra 15 (1987), 713–750.CrossRefGoogle Scholar
[10]Mahdavianary, S. K.. A classification of 2-generator p-groups, p ≥ 3, with many subgroups 2-subnormal. Arch. Math. (Basel) 43 (1984), 97–107.CrossRefGoogle Scholar
[11]Thomas, Meixner. Power automorphisms of finite p-groups. Israel J. Math. 38 (1981), 345–360.Google Scholar
[12]Newman, M. F. and O'Brien, E. A.. The Wielandt length of some 3-groups. SIGSAM Bull. 25 (1991), 50–51.CrossRefGoogle Scholar
[13]Ormerod, Elizabeth A.. The Wielandt subgroup of metacyclic p-groups. Bull. Austral. Math. Soc. 42 (1990), 499–510.CrossRefGoogle Scholar
[14]Schenkman, E.. On the norm of a group. Illinois J. Math. 4 (1960), 150–152.CrossRefGoogle Scholar
[15]Wielandt, H.. Uber den Normalisator der subnormalen Untergruppen. Math. Z. 69 (1958), 463–465.CrossRefGoogle Scholar