Hostname: page-component-788cddb947-w95db Total loading time: 0 Render date: 2024-10-09T18:10:17.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Isolated singular points in the theory of algebraic surfaces

Published online by Cambridge University Press:  24 October 2008

D. W. Babbage
D. W. Babbage
Affiliation:
Magdalene College
Get access Rights & Permissions [Opens in a new window]

Extract

If F(x0, x1, x2, x3) = 0 is the equation of a surface in space of three dimensions which has an ordinary isolated s-ple point O, then by means of the substitutions

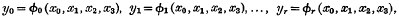
where Φ0 = 0, Φ1 = 0, …, Φr = 0 are the equations of r + 1 linearly independent surfaces passing simply through O, F is transformed into a surface F′ in [r], on which to the point O of F there corresponds a simple curve γ. The points of γ arise from the points of F in the first neighbourhood of O, and in this simple case the genus of γ is ½ (s − 1) (s − 2). In the study of properties which are common to all members of an infinite family of birationally equivalent surfaces no distinction is made between O and γ, O being regarded as a curve which has become infinitesimal on the particular surface of the family in question.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 2 , May 1933 , pp. 212 - 230
Copyright
Copyright © Cambridge Philosophical Society 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Enriques, , Lezioni sulla teoria delle superficie algebriche, Padova (1932), § 4, p. 17.Google Scholar As we shall frequently refer to this book such a reference as this will in future be denoted for brevity by E(4) 17.

* Cf. E (38).

† By a point of accidental singularity is meant one which belongs to two or more distinct sheets of the surface. Such a point is to be regarded as the accidental point of coincidence in space of two or more distinct points of the surface.

‡ Segre, , “Intorno ad un carattere delle superficie”, Atti dell' Accad. d. Scienze di Torino, 31 (1895), 341–357Google Scholar.

* This number is given incorrectly as 2ρ − 2 + ki by Castelnuovo, and Enriques, , Annali di Mat. (3), 6 (1901), 165–225 (187).CrossRefGoogle Scholar

† Castelnuovo and Enriques, loc. cit.

* This expression for μ2 was given by Professor H. F. Baker in the course of a series of lectures on the theory of surfaces in the Lent term, 1932.

† That is, points, such as tacnodes, which are transformed, by means of a linear system of surfaces passing simply through them, into multiple curves of the transformed surface.

‡ Cf. E, cap. ii.

* A general sum of Σ consists of a curve K together with e rational curves which have no intersections with K or with each other; the genus of this composite curve is p (1) − e.

† E(28).

* We use the notation of the preceding paragraph for the order, rank, class, etc. of F.

† Cf. E (35) 129.

* The condition of adjointness at an s-ple point O can also be found if we use a net cut by planes through O. All curves of the net are of the form + O. We remove the common part O, and the Jacobian j of || has in this case s (s + 1) branches at O. Hence j − 3, O = s (s + 1) −s = s (s − 2), as before. See E (35) 129–130.

* Nöther, , Math. Ann. 8 (1875), 495–533.CrossRefGoogle Scholar

* C has a tacnode at O.

* This is in contradiction with E (39) 150–151. Enriques' argument, though attractive, seems to me unconvincing.

† These two statements can be illustrated by means of nets of curves in a plane. The Jacobian of the net contains the factor θ3 = 0, and the Jacobian of the net contains the factor

* See § 2.

* ′ has a tacnode at O, the tangent being the special line through O.

* One plane of the asymptotic cone at each biplanar point contains the line l.

* In the example that we have taken, where F is of order s + 1, the curve J projects from O into a curve of order s + 1 in the plane passing simply through the points P 1, P 2, …, P s+1.

* The transformation into a proper elliptic curve can be effected by means of surfaces which touch the tacnodal plane at the tacnode. If quadric surfaces are used these can be represented by the prime sections of the point-cone in [6] whose cross-section is a Veronese surface. F will be represented by a surface on this cone and its tacnode by an elliptic quartic curve lying on-one of the quadric cones of .

* If the equation of F is taken as

the surfaces which cut out |G J| will be of the form

* E (60) 378.