Hostname: page-component-5c6d5d7d68-7tdvq Total loading time: 0 Render date: 2024-08-15T21:21:50.657Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal inequalities of Kahane–Khintchine's type in Orlicz spaces

Published online by Cambridge University Press:  24 October 2008

Goran Peškir
Goran Peškir
Affiliation:
Department of Mathematics, University of Zagreb, P.O. Box 635, 41000 Zagreb, Croatia and University of Aarhus, Ny Munkegade, 8000 Aarhus, Denmark
Get access Rights & Permissions [Opens in a new window]

Abstract

Several maximal inequalities of Kahane–Khintchine's type in certain Orlicz spaces are proved. The method relies upon Lévy's inequality and the technique established in [14] which is obtained by Haagerup–Young–Stechkin's best possible constants in the classical Khintchine inequalities. Moreover by using Donsker's invariance principle it is shown that the numerical constant in the inequality deduced by the method presented is nearly optimal: If 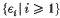is a Bernoulli sequence, and ‖ · ‖ψ denotes the Orlicz norm induced by the function 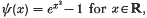then the following inequality is satisfied:

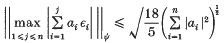
for all a1,…, an and all n ≥ 1, and the best possible numerical constant which can take the place of 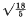lies in the interval ]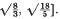. Sharp estimates of this type are also deduced for some other maximal inequalities in Orlicz spaces discovered in this paper.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 175 - 190
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Billngsley, P.. Convergence of Probability Measures (John Wiley, 1968).Google Scholar
[2]Edgar, G. A. and Sucheston, L.. On maximal inequalities in Orlicz spaces. Measure and Measurable Dynamics. Proc. Conf. Rochester, Contemp. Math. 94 (1989), 113–129.CrossRefGoogle Scholar
[3]Gluskin, E. D., Pietsch, A. and Puhl, J.. A generalization of Khintchine's inequality and its application in the theory of operator ideals. Studia Math. 67 (1980), 149–155.CrossRefGoogle Scholar
[4]Graversen, S. E., Peškir, G. and Weber, M.. The continuity principle in exponential type Orlicz spaces. Institute of Mathematics, University of Aarhus, Preprint Series 32 (1992).Google Scholar
[5]Haagerup, U.. The best constants in the Khintchine inequality. Studia Math. 70 (1982), 231–283.CrossRefGoogle Scholar
[6]Hoffmann-Jørgensen, J.. Function norms. Institute of Mathematics, University of Aarhus, Preprint Series 40 (1991).Google Scholar
[7]Hoffmann-Jørgensen, J.. Inequalities for sums of random elements. Institute of Mathematics, University of Aarhus, Preprint Series 41 (1991).Google Scholar
[8]Hoffmann-Jørgensen, J.. Probability theory with a view to statistics (Chapman and Hall), to appear.Google Scholar
[9]Johnson, W. B., Schechtman, G. and Zinn, J.. Best constants in moment inequalities for linear combinations of independent and exchangeable random variables. Ann. Probab. 13 (1985), 234–253.CrossRefGoogle Scholar
[10]Kahane, J. P.. Some Random Series of Functions (D. C. Heath & Co., 1968, 1st edn, and Cambridge University Press, 1985, 2nd edn).Google Scholar
[11]Komorowski, R.. On the best possible constants in the Khintchine inequality for p ≥ 3. Bull. London Math. Soc. 20 (1988), 73–75.CrossRefGoogle Scholar
[12]Krasnosel'skii, M. A. and Rutickii, Ya. B.. Convex Functions and Orlicz Spaces (P. Noordhoff Ltd., 1961).Google Scholar
[13]Marcus, M. B. and Pisier, G.. Stochastic processes with sample paths in exponential Orlicz spaces. Probability in Banach spaces V, Lecture Notes in Math. vol. 1153 (Springer-Verlag, 1985), pp. 328–358.CrossRefGoogle Scholar
[14]Peškir, G.. Best constants in Kahane–Khintchine inequalities in Orlicz spaces. J. Multivariate Anal. 45, 2 (1993), 183–216.CrossRefGoogle Scholar
[15]Pick, L.. Two-weight weak type maximal inequalities in Orlicz classes. Studia Math. 100 (1992), 207–218.CrossRefGoogle Scholar
[16]Rao, M. M. and Ren, Z. D.. Theory of Orlicz Spaces (Marcel Dekker, 1991).Google Scholar
[17]Rodin, V. A. and Semyonov, E. M.. Rademacher series in symmetric spaces. Analysis Mathematica 1 (1975), 207–222.CrossRefGoogle Scholar
[18]Sawa, J.. The best constant in the Khintchine inequality for complex Steinhaus variables, the case p = 1. Studia Math. 81 (1985), 107–126.CrossRefGoogle Scholar
[19]Stechkin, S. B.. On the best lacunary systems of functions. Izv. Akad. Nauk SSSR, Ser. Mat. 25 (1961), 357–366 (in Russian).Google Scholar
[20]Szarek, S. J.. On the best constant in the Khintchine inequality. Studia Math. 58 (1978), 197–208.CrossRefGoogle Scholar
[21]Tignol, J. P.. Galois' Theory of Algebraic Equations (Institut de Mathématique Pure et Appliquée, UCL, Louvain-la-Neuve, Belgium, 1988).Google Scholar
[22]Weber, M.. Analyse infinitesimale de fonctions aleatoires. Ecole d'eté Probabilités de Saint-Flour XI, Lecture Notes in Math., vol. 976 (Springer-Verlag, 1983), pp. 383–465.Google Scholar
[23]Young, R. M. G.. On the best possible constants in the Khintchine inequality. J. London Math. Soc. 14 (1976), 496–504.CrossRefGoogle Scholar