Hostname: page-component-5c6d5d7d68-wp2c8 Total loading time: 0 Render date: 2024-08-16T05:27:20.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-singular models of specialized Weddle surfaces

Published online by Cambridge University Press:  24 October 2008

W. L. Edge
W. L. Edge
Affiliation:
University of Edinburgh
Get access Rights & Permissions [Opens in a new window]

Extract

There are, in projective space Σ of three dimensions, two famous quartic surfaces: W, the Weddle surface with six nodes ((13), p. 69, footnote) and K, the Kummer surface with sixteen ((s), p. 246, (7) passim). They are in birational correspondence and have the same non-singular model: the octavic base surface F of the net of quadrics in [5], which contain a given line λ and for which a given simplex S is self-polar ((5); (6)). One naturally takes S, with vertices X0, X1, X2, X3, X4, X5 as simplex of reference for homogeneous coordinates x0, x1, x2, x3, x4, x5; F is invariant under the harmonic inversions hj in the vertices Xj and opposite bounding primes xj = 0 of S. These six hj, mutually commutative and having identity for their product, generate an elementary abelian group 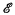of order 32. This representation of 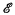throws into prominence what may, in this context, be called its positive subgroup 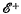, of order 16, consisting of identity and the 15 products hjhk = hkhj; these are harmonic inversions in the edges XjXk and opposite bounding solids xj = xk = 0 of S. The coset of 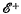consists of the six hj and their ten products in threes, complementary products being the same (h0h1h2 ≡ h3h4h5) because of the product of all six hj being identity. These ten products are harmonic inversions in the ten pairs of opposite plane faces of S.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 3 , November 1976 , pp. 399 - 418
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, H. F.Elementary note on the Weddle quartic surface. Proc. London Math. Soc. (2) 1 (1903), 247–261.Google Scholar
(2)Baker, H. F.Principles of geometry, vol. IV (Cambridge, 1925 and 1940).Google Scholar
(3)Cayley, A.Sur la surface des ondes. Journal de mathématiques 11 (1846), 291–296; Collected Papers, 1, 302–305.Google Scholar
(4)Cayley, A.A memoir on quartic surfaces. Proc. London Math. Soc. 3 (1870), 19–69; Collected Papers, VII, 133–181.Google Scholar
(5)Edge, W. L.Baker's property of the Weddle surface. J. London Math. Soc. 32 (1957), 463–466.Google Scholar
(6)Edge, W. L.A new look at the Kummer surface. Canal. J. Math. 19 (1967), 952–967.CrossRefGoogle Scholar
(7)Hudson, R. W. H. T.Kummer's quartic surface (Cambridge, 1905).Google Scholar
(8)Kummer, E. E. Über die Flächen vierten Grades mit sechzehn singularen Punkten. Monatsberichte der königlich preussischen Akademie der Wissenschaften zu Berlin (1865).Google Scholar
(9)Rohn, K.Einige specielle Fälle der Kummerschen Fläche. Berichte über die Verhandlungen der königlich sächsischen Gesellschaft der Wissenschaften zu Leipzig (Mathematisch-Physische Klasse) 36 (1884), 10–16.Google Scholar
(10)Segre, C.Sur un cas particulier de la surface de Kummer. Berichte über die Verhandlungen der königlich sächsischen Gesellschaft der Wissenschaften zu Leipzig (Mathematisch-Physische Klasse) 36 (1884), 132–135; Opere, vol. In (Rome 1961), 502–505.Google Scholar
(11)Snyder, V.An application of a (1, 2) quaternary correspondence to the Weddle and Kummer surfaces. Trans. Amer. Math. Soc. 12 (1911), 354–366.Google Scholar
(12)Tyrrell, J. A. and Semple, J. G.Generalized Clifford parallelism (Cambridge, 1971).Google Scholar
(13)Weddle, T.On the theorems in space analogous to those of Pascal and Brianchon in a plane: Part II. Cambridge and Dublin Math. J. 5 (1850), 58–69.Google Scholar