Hostname: page-component-5c6d5d7d68-vt8vv Total loading time: 0.001 Render date: 2024-08-16T08:22:30.551Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Product of Three Homogeneous Linear Forms. IV

Published online by Cambridge University Press:  24 October 2008

H. Davenport
H. Davenport
Affiliation:
University College of North WalesBangor
Get access Rights & Permissions [Opens in a new window]

Extract

Let L1, L2, L3 be three homogeneous linear forms in u, v, w with real coefficients and determinant 1. Let M denote the lower bound of

for integral values of u, v, w, not all zero. I proved a few years ago (1) that

more precisely, that

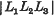
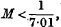
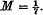except when L1, L2, L3 are of a special type, in which case If we denote by θ, ø, ψ the roots of the cubic equation t3+t2-2t-1 = 0, the special linear forms are equivalent, by an integral unimodular linear transformation, to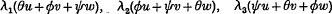

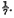(in any order), where λ1,λ2,λ3 are real number whose product is In this case, L1L2L3|λ1λ2λ3 is a non-zero integer, and the minimum of its absolute value is 1, giving

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 39 , Issue 1 , March 1943 , pp. 1 - 21
Copyright
Copyright © Cambridge Philosophical Society 1943

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Proc. London Math. Soc. (2), 44 (1938), 412–31.Google Scholar
(2)Journal London Math. Soc. 17 (1942), 107–15.Google Scholar
(3)Journal London Math. Soc. 16 (1941), 98–101.Google Scholar
(4)For some results on the other conjectures, see Davenport, , Proc. Cambridge Phil. Soc. 37 (1941), 325–30.CrossRefGoogle Scholar
(5)The quadratic form is X 2 + Y 2 + (X + Y)2, where X, Y are linear forms in v, w with determinant (1 − ε)/M. (6) I adopt the convention that θ = 1·246… means 1·246<θ< 1·247, and ø = − 0·445… means − 0·446<ø< −0·445.Google Scholar
(7)The argument which follows is a simplification of that in § 7 of the previous paper (1).Google Scholar
(8)It is easily verified that − øψ − 1 or −θ−1 − 1 satisfies the same cubic equation as θ, and since it lies between − 2 and − 1, it must equal ψ. Alternatively, the result follows from the fact that θ = 2 cos 2π/7, ø = 2 cos 4π/7, ψ = 2 cos 6π/7.Google Scholar
(9)This may be proved as in (8); the cyclotomic values of θ′, ø′, ψ′ are θ′ = 2 cos π/9, ø′ = 2 cos 5π/9, ψ′ = 2 cos 7π/9.Google Scholar