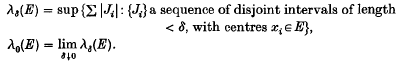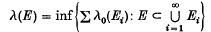Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Raymond, Xavier Saint
and
Tricot, Claude
1988.
Packing regularity of sets in n-space.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 103,
Issue. 1,
p.
133.
Cutler, C. D.
1991.
Some results on the behavior and estimation of the fractal dimensions of distributions on attractors.
Journal of Statistical Physics,
Vol. 62,
Issue. 3-4,
p.
651.
Talagrand, Michel
and
Xiao, Yimin
1996.
Fractional Brownian motion and packing dimension.
Journal of Theoretical Probability,
Vol. 9,
Issue. 3,
p.
579.
Xiao, Yimin
1996.
Packing dimension, Hausdorff dimension and Cartesian product sets.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 120,
Issue. 3,
p.
535.
Joyce, H.
1998.
A relationship between packing and topological dimensions.
Mathematika,
Vol. 45,
Issue. 1,
p.
43.
Tyson, Jeremy
2001.
Metric and geometric quasiconformality in Ahlfors regular Loewner spaces.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 5,
Issue. 3,
p.
21.
Zhiwei, Zhu
and
Zuoling, Zhou
2002.
The Hausdorff Centred measure of the symmetry Cantor sets.
Approximation Theory and its Applications,
Vol. 18,
Issue. 2,
p.
49.
Feng, De–Jun
2003.
Exact packing measure of linear Cantor sets.
Mathematische Nachrichten,
Vol. 248-249,
Issue. 1,
p.
102.
Jia, Baoguo
Zhou, Zuoling
Zhu, Zhiwei
and
Luo, Jun
2003.
The packing measure of the Cartesian product of the middle third Cantor set with itself.
Journal of Mathematical Analysis and Applications,
Vol. 288,
Issue. 2,
p.
424.
Baoguo, Jia
and
Zhiwei, Zhu
2004.
The packing measure of a class of generalized sierpinski carpet.
Analysis in Theory and Applications,
Vol. 20,
Issue. 1,
p.
69.
Qu, Cheng-Qin
Zhou, Zuo-Ling
and
Jia, Bao-Guo
2004.
The upper densities of symmetric perfect sets.
Journal of Mathematical Analysis and Applications,
Vol. 292,
Issue. 1,
p.
23.
Baek, Hun Ki
2008.
Regularities of multifractal measures.
Proceedings Mathematical Sciences,
Vol. 118,
Issue. 2,
p.
273.
Zhu, Zhiwei
and
Zhou, Zuoling
2008.
The exact measures of a class of self-similar sets on the plane.
Analysis in Theory and Applications,
Vol. 24,
Issue. 2,
p.
160.
Tricot, Claude
2010.
General Hausdorff functions, and the notion of one-sided measure and dimension.
Arkiv för Matematik,
Vol. 48,
Issue. 1,
p.
149.
LLORENTE, MARTA
and
MORÁN, MANUEL
2016.
Computability of the packing measure of totally disconnected self-similar sets.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 5,
p.
1534.
Llorente, Marta
Eugenia Mera, M.
and
Morán, Manuel
2017.
Rate of convergence: the packing and centered Hausdorff measures of totally disconnected self-similar sets.
Chaos, Solitons & Fractals,
Vol. 98,
Issue. ,
p.
220.
Reid, James E.
2018.
Packing measure of super separated iterated function systems.
Geometriae Dedicata,
Vol. 197,
Issue. 1,
p.
173.
Llorente, Marta
Mera, M Eugenia
and
Morán, Manuel
2018.
On the packing measure of the Sierpinski gasket.
Nonlinearity,
Vol. 31,
Issue. 6,
p.
2571.
Douzi, Zied
and
Selmi, Bilel
2019.
Regularities of general Hausdorff and packing functions.
Chaos, Solitons & Fractals,
Vol. 123,
Issue. ,
p.
240.
Selmi, Bilel
2019.
On the strong regularity with the multifractal measures in a probability space.
Analysis and Mathematical Physics,
Vol. 9,
Issue. 3,
p.
1525.