Ramanujan's Continued Fraction may be stated as follows: Let where there are eight gamma functions in each product and the ambiguous signs are so chosen that the argument of each gamma function contains one of the specified number of minus signs. Then 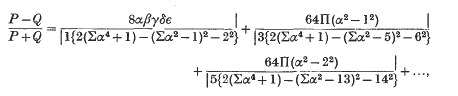where the products and the sums on the right range over the numbers α, β, γ, δ, ε: provided that one of the numbers β, γ, δ, ε is equal to ± ±n, where n is a positive integer. In 1935, Watson (3) proved the theorem by induction and also gave a basic analogue. In this paper we give a new proof of Ramanujan's Continued Fraction by using the transformation of Bauer and Muir in the theory of continued fractions (Perron (1), §7;(2), §2).