Hostname: page-component-7bb8b95d7b-pwrkn Total loading time: 0 Render date: 2024-10-06T14:15:14.539Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple proof of Müntz's theorem

Published online by Cambridge University Press:  24 October 2008

L. C. G. Rogers
L. C. G. Rogers
Affiliation:
University of Warwick
Get access Rights & Permissions [Opens in a new window]

Extract

Let 0 < λ1 < λ2 < … be an increasing sequence of positive reals tending to infinity, and let ν1, ν2 be two (finite) signed measures on ℝ+ such that

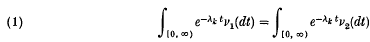
for all k. It was originally proved by Müntz (12) that, if

then ν1 = ν2, and, conversely, if this condition fails, then there exist distinct ν1 and ν2 satisfying (1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 1 , July 1981 , pp. 1 - 3
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Akutowicz, E. J.The completeness of spaces of Dirichlet series with sufficiently sparse complex exponents. J. Math. Anal. 39 (1972), 445–454.Google Scholar
(2)Aupetit, B. H.Théorème de Müntz pour les fonctions de plusieurs variables. Canad. Math. Bull. 16 (1973), 165–166.CrossRefGoogle Scholar
(3)Carleman, T.Über die Approximation analytischer Funktionen durch lineare Aggregate von Potenzen. Ark. Mat. 17 (1923), 14–17.Google Scholar
(4)Feller, W.On Müntz' theorem and completely monotone functions. Amer. Math. Monthly 75 (1968), 342–350.Google Scholar
(5)Ferguson, L. B. O. and Von Golitschek, M.Le théorème de Müntz-Szász avec coefficients entiers. C.R. Acad. Sci. Paris A 279 (1974), 817–818.Google Scholar
(6)Von Golitschek, M.The degree of approximation for generalised polynomials with integral coefficients. Trans. Amer. Math. Soc. 224 (1976), 417–425.CrossRefGoogle Scholar
(7)Hirschman, I. I. and Widder, D. V.Generalised Bernstein polynomials. Duke Math. J. 16 (1949), 433–438.Google Scholar
(8)Kaczmarcz, S. and Steinhaus, H.Theorie der Orthogonalreihen (Warsaw, 1935).Google Scholar
(9)Korevaar, J. and Dixon, M.Non spanning sets of exponentials on curves. Acta Math. Acad. Sci. Hung. 33 (1979), 89–100.CrossRefGoogle Scholar
(10)Lorentz, G. G.Bernstein polynomials. (Mathematical Expositions, Vol. 8 Toronto, 1953).Google Scholar
(11)Luxemburg, W. A. J. and Korevaar, J.Entire functions and Müntz-Szász type approximation. Trans. Amer. Math. Soc. 157 (1971), 23–37.Google Scholar
(12)Müntz, C. H. Über den Approximationssatz von Weierstrass. Math. Abhandlungen H. A. Schwartz Festschrift (Berlin, 1914).Google Scholar
(13)Paley, R. E. A. C. and Wiener, N.Fourier transforms in the complex domain (A.M.S. Colloquium Publications, New York, 1934).Google Scholar
(14)Schwartz, L.Étude des Sommes d'Exponentielles. (Actualités Sci. Indust. 959 1943).Google Scholar
(15)Szász, O.Über die Approximation Stetiger Funktionen durch lineare Aggregate von Potenzen. Math. Ann. 77 (1916), 482–496.Google Scholar