Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-22T20:19:16.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Some recent developments concerning asymptotic distributions of pontograms

Published online by Cambridge University Press:  24 October 2008

Vera R. Eastwood
Vera R. Eastwood
Affiliation:
Acadia University, Wolfville, N. S., Canada
Get access Rights & Permissions [Opens in a new window]

Extract

The data analytical problem of testing whether an empirical set of n given points in the plane could be considered to contain too many straight line configurations in a situation where the generating mechanism of the n points is unknown, was recently reintroduced to the literature by D. G. Kendall and W. S. Kendall[7]. Taking the Land's end data problem (cf. also Broadbent [1] and further references given there) as the anchor point and motivation for their discussion, D. G. and W. S. Kendall developed a new testing device, called the pontogram. The pontogram is a one- parameter stochastic process defined pointwise by

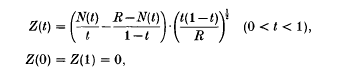
where N denotes a Poisson process in [0, 1] with N(0) = 0 and unknown intensity parameter μ > 0 and where R = N(1) gives the number of Poisson events in the entire [0, 1] section.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 108 , Issue 3 , November 1990 , pp. 559 - 567
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Broadbent, S.. Simulating the Ley Hunter. J. Roy. Statist. Soc. Ser. A 143 (1980), 109–140.CrossRefGoogle Scholar
[2]Csörgö, M. and Horváth, L.. On the distributions of Lp norms of weighted uniform empirical and quantile processes. Ann. Probab. 16 (1988), 142–161.CrossRefGoogle Scholar
[3]Csörgö, M. and Horváth, L.. Asymptotic distributions of pontograms. Math. Proc. Cambridge Philos. Soc. 101 (1987), 131–139.CrossRefGoogle Scholar
[4]Csörgö, M., Horváth, L. and Steinebach, J.. Invariance principles for renewal processes. Ann. Probab. 15 (1987), 1441–1460.CrossRefGoogle Scholar
[5]Csörgö, M., Horváth, L. and steinebach, J.. Strong approximations for renewal processes. C. R. Math. Rep. Acad. Sci. Canada 8 (1986), 151–154.Google Scholar
[6]Huse, V. R.. On some nonparametric methods for changepoint problems. Ph.D. thesis, Carleton University, Ottawa (1988).Google Scholar
[7]Kendall, D. G. and Kendall, W. S.. Alignments in two-dimensional random sets of points. Adv. in Appl. Probab. 12 (1980), 380–424.CrossRefGoogle Scholar
[8]Steinebach, J.. Improved Erdös–Rényi and strong approximation laws for increments of renewal processes. Ann. Probab. 14 (1986), 547–559.CrossRefGoogle Scholar
[9]Steinebach, J.. Erdös–Rényi–Zuwächse bei Erneuerungsprozessen und Partialsummen auf Gittern. Habilitationsschrift, Universität Düsseldorf (1979).Google Scholar