Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-29T05:41:56.862Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic functions of finite dimensional linear transformations

Published online by Cambridge University Press:  24 October 2008

S. N. Afriat
S. N. Afriat
Affiliation:
The Hebrew University of JerusalemPrinceton University
Get access Rights & Permissions [Opens in a new window]

Extract

Since the first introduction of the concept of a matrix, questions about functions of matrices have had the attention of many writers, starting with Cayley(i) in 1858, and Laguerre(2) in 1867. In 1883, Sylvester(3) defined a general function φ(a) of a matrix a with simple characteristic roots, by use of Lagrange's interpolation formula, and Buchheim (4), in 1886, extended his definition to the case of multiple characteristic roots. Then Weyr(5) showed in 1887 that, for a matrix a with characteristic roots lying inside the circle of convergence of a power series φ(ζ), the power series φ(a) is convergent; and in 1900 Poincaré (6) obtained the formulae

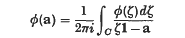
for the sum, where C is a circle lying in and concentric with the circle of convergence, and containing all the characteristic roots in its ulterior, such a formula having effectively been suggested by Frobenius(7) in 1896 for defining a general function of a matrix. Phillips (8), in 1919, discovered the analogue, for power series in matrices, of Taylor's theorem. In 1926 Hensel(9) completed the result of Weyr by showing that a necessary and sufficient condition for the convergence of φ(a) is the convergence of the derived series φ(r)(α) (0 ≼ r < mα; α) at each characteristic root α of a, of order r at most the multiplicity mα of α. In 1928 Giorgi(10) gave a definition, depending on the classical canonical decomposition of a matrix, which is equivalent to the contour integral formula, and Fantappie (11) developed the theory of this formula, and obtained the expression

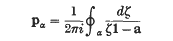
for the characteristic projectors.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 55 , Issue 1 , January 1959 , pp. 51 - 61
Copyright
Copyright © Cambridge Philosophical Society 1959

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cayley, A.A memoir on the theory of matrices. Phil. Trans. 148 (1858), 17–37. (Collected Mathematical Papers, II, 475–96.)Google Scholar
(2)Laguerre, E. N.Sur le calcul des systémes linèares. J. Ècole Polytech. 42 (1867), 215–64. (Oeuvres, I, 221–67.)Google Scholar
(3)Sylvester, J. J.On the equation to the secular inequalities in the planetary theory. Phil. Mag. (5), 16 (1883), 267–9. (Collected Mathematical Papers, IV, 110–11.)CrossRefGoogle Scholar
(4)Buchheim, A.An extension of a theorem of Professor Sylvester's relating to matrices. Phil. Mag. (5), 22 (1886), 173–4.CrossRefGoogle Scholar
(5)Weyr, E.Bull. Sci. Math. 11 (1887), 205–15.Google Scholar
(6)Poincaré, H.Sur les groupes continus. Trans. Camb. Phil. Soc. 18 (1900), 220–55.Google Scholar
(7)Frobenius, G.Über die cogredienten Transformationen der bilinearen Formen. Berl. Sitz. (1896), pp. 601–14.Google Scholar
(8)Phillips, H. B.Functions of matrices. Amer. J. Math. 41 (1918), 266–78.CrossRefGoogle Scholar
(9)Hensel, K.J. reine angew. Math. 155 (1926), 107–10.Google Scholar
(10)Giorgi, G.Atti Accad. Naz. Lincei, vi, 8 (1928), 3–8.Google Scholar
(11)FantappiÉ, L.La calcul des matrices. C.R. Acad. Sci., Paris, 186 (1928), 619–21.Google Scholar
(12)Cipolla, M.R. C. Circ. mat. Palermo, 56 (1932), 144–54.Google Scholar
(13)MacDuffee, C. C.Theory of matrices (New York, 1946).Google Scholar
(14)Lorch, E. R.The spectrum of linear transformations. Trans. Amer. Math. Soc. 52 (1942), 238–48.Google Scholar
(15)Dunford, N.Spectral theory. I. Trans. Amer. Math. Soc. 54 (1943), 85–217.Google Scholar
(16)Taylor, A. E.Analysis in complex Banach spaces. Bull. Amer. Math. Soc. 49 (1943), 652–69.Google Scholar
(17)Hamburger, H. L. and Grimshaw, M. E.Linear transformations in n-dimensional vector space (Cambridge, 1951).Google Scholar
(18)Ferrar, W. L.Finite matrices (Oxford, 1951).Google Scholar
(19)Mirsky, L.An introduction to linear algebra (Oxford, 1955).Google Scholar
(20)Afriat, S. N.Composite matrices. Quart. J. Math. (2), 5 (1954), 81–98.CrossRefGoogle Scholar
(21)Afriat, S. N.Bounds for the characteristic values of matrix functions. Quart. J. Math. (2), 2 (1951), 81–4.CrossRefGoogle Scholar
(22)Oldenberger, R.Infinite powers of matrices and infinite roots. Duke Math. J. 6 (1940), 257.Google Scholar
(23)Wedderburn, J. H. M.Lectures on matrices (American Math. Soc. Coll. Publ. xviii, 1934).CrossRefGoogle Scholar