Recently, Lutz and Stull used methods from algorithmic information theory to prove two new Marstrand-type projection theorems, concerning subsets of Euclidean space which are not assumed to be Borel, or even analytic. One of the theorems states that if 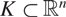\[K \subset {\mathbb{R}^n}\] is any set with equal Hausdorff and packing dimensions, then

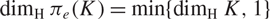\begin{equation} \[{\dim _{\text{H}}}{\pi _e}(K) = \min \{ {\dim _{\text{H}}}{\text{ }}K{\text{, 1}}\} \] \end{equation}

for almost every 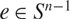\[e \in {S^{n - 1}}\]. Here 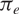\[{\pi _e}\] stands for orthogonal projection to span (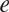\[e\]). The primary purpose of this paper is to present proofs for Lutz and Stull’s projection theorems which do not refer to information theoretic concepts. Instead, they will rely on combinatorial-geometric arguments, such as discretised versions of Kaufman’s “potential theoretic” method, the pigeonhole principle, and a lemma of Katz and Tao. A secondary purpose is to generalise Lutz and Stull’s theorems: the versions in this paper apply to orthogonal projections to m-planes in 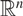\[{\mathbb{R}^n}\], for all 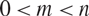\[0 < m < n\].