Hostname: page-component-5c6d5d7d68-txr5j Total loading time: 0 Render date: 2024-08-14T17:48:51.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Improving certain simple eigenvalue bounds

Published online by Cambridge University Press:  24 October 2008

Seppo Hyydö ,
Jorma Kaarlo Merikoski  and
Ari Virtanen
Seppo Hyydö
Affiliation:
University of Tampere, Finland
Jorma Kaarlo Merikoski
Affiliation:
University of Tampere, Finland
Ari Virtanen
Affiliation:
University of Tampere, Finland
Get access Rights & Permissions [Opens in a new window]

Extract

Throughout this paper we let A = (aij) be a non-zero n × n matrix-we study real matrices only–with row sums R1,…Rn and eigenvalues λ1,…,λn, ordered λ1≥…≥λn if they are real. We denote E = (1,…,1)T and su A = ΣiΣjaij = ETAE. If A is symmetric, a simple property of the Rayleigh quotient is that

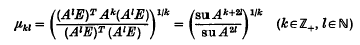
satisfies

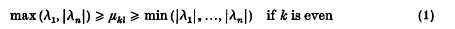
and

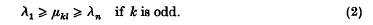
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 3 , May 1986 , pp. 507 - 518
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atkinson, F. V., Watterson, G. A. and Moran, P. A. P.. A. matrix inequality. Quart. J. Math. Oxford 11 (1960), 137–140.CrossRefGoogle Scholar
[2]Berman, A. and Plemmons, R. J.. Nonnegative Matrices in the Mathematical Sciences (Academic Press, 1979).Google Scholar
[3]Deutsch, E.. Lower bounds for the Perron root of a non-negative irreducible matrix. Math. Proc. Cambridge Philos. Soc. 92 (1982), 49–54.CrossRefGoogle Scholar
[4]Kankaanpää, H. and Merikoski, J. K.. Two inequalities for the sum of elements of a matrix. Linear and Multilinear Algebra 18 (1985), 9–22.CrossRefGoogle Scholar
[5]London, D.. Inequalities in quadratic forms. Duke Math. J. 33 (1966), 511–522.CrossRefGoogle Scholar
[6]London, D.. Two inequalities in nonnegative symmetric matrices. Pacific J. Math. 16 (1966), 515–536.Google Scholar
[7]Marcus, M. and Newman, M.. The sum of the elements of the powers of a matrix. Pacific J. Math. 12 (1962), 627–635.CrossRefGoogle Scholar
[8]Merikoshi, J. K.. On a lower bound for the Perron eigenvalue. BIT 19 (1979), 39–42.CrossRefGoogle Scholar
[9]Mirsky, L.. The spread of a matrix. Mathematika 3 (1956), 127–130.Google Scholar
[10]Mulholland, H. P. and Smith, C. A. B.. An inequality arising in genetical theory. Amer. Math. Monthly 66 (1959), 673–683.Google Scholar
[11]Parker, W. V.. Sets of complex numbers associated with a matrix. Duke Math. J. 15 (1948), 711–715.Google Scholar
[12]Wilkinson, J. H.. Householder's method for symmetric matrices. Numer. Math. 4 (1962), 354–361.Google Scholar
[13]Wolkowicz, H. and Styan, G. P. H.. Bounds for eigenvalues using traces. Linear Algebra Appl. 29 (1980), 471–506.Google Scholar