Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-21T04:29:35.628Z Has data issue: false hasContentIssue false
  • English
  • Français

On Ext1 for semisimple groups and infinitesimal subgroups

Published online by Cambridge University Press:  24 October 2008

Stephen Donkin
Stephen Donkin
Affiliation:
King's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be an affine, connected, semisimple, simply connected algebraic group over an algebraically closed field k of non-zero characteristic p and, for a positive integer n, let Gn be the nth infinitesimal subgroup (the kernel of the nth power of the Frobenius morphism). The purpose of this note is to point out that, for certain rational G-modules V, the natural homomorphism

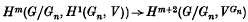
is the zero map, for m ≽ 0. For such modules V, taking m = 0, we see from the 5-term exact sequence of Lyndon-Hochschild-Serre that the inflation-restriction sequence

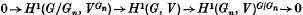
is exact and thus the dimension of H1(G, V), when finite, may be calculated by adding the dimensions of the outer terms. The practical value of this result seems to lie in the special case n = 1 and V = L(λ) ⊗ L(µ), the tensor product of simple rational G-modules. In this case H1(G/G1) VG1 is H1(G, L(λ′) ⊗ L(¯′)) for λ′, ¯′ ‘smaller’ than λ µ and the above exact sequence gives an inductive procedure for computing Ext1G between simple rational (G-modules once the (G-module structure of Ext1G1 (equi valently Ext1u1 where% is the restricted enveloping algebra of the Lie algebra of G), for simple G1-modules, is known. Using the rather complicated structure of Weyl modules Cline, in (4), calculated Ext1G between simple modules for G = SL2(k) (this process was reversed in (5)). The present note has been used by S. EIB. Yehia, (17), in finding the corresponding result for SL3(k). We believe these Ext groups to be of increasing importance in view of their connection with Lusztig's conjecture, (14), on the characters of the simple rational G-modules and the related conjecture, 7–2 of (l), of Andersen.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 92 , Issue 2 , September 1982 , pp. 231 - 238
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Andersen, H. H. Line bundles on flag manifolds. (To appear.)Google Scholar
(2)Ballard, J. W.Injective modules for restricted enveloping algebras. Math. Z. 163 (1978), 57–63.CrossRefGoogle Scholar
(3)Chevalley, C. Certains schémas de groupes semi-simples. Sém. Bourbaki 13éme annfée (1960–1961), exp. 219.Google Scholar
(4)Cline, E.Ext1 for SJ 2. Communications in Algebra 7 1) (1979), 107–111.CrossRefGoogle Scholar
(5)Cline, E. A second look at Weyl modules for SL 2. (To appear.)Google Scholar
(6)Cline, E., Parshall, B. and Scott, L.Cohomology, hyperalgebras and representations. J. Alg. 63 (1980), 98–123.CrossRefGoogle Scholar
(7)Donkin, S.Hopf complements and injective comodules for algebraic groups. Proc. London Math. Soc. (3), 40 1980), 298–319.CrossRefGoogle Scholar
(8)Donkin, S.The blocks of a semisimple algebraic group. J. Alg. 67 (1980), 36–53.CrossRefGoogle Scholar
(9)Green, J. A.Locally finite representations. J. Alg. 41 (1976), 137–171.CrossRefGoogle Scholar
(10)Grothendieck, A.Sur quelques points d'algèbre homologique, Tohoku Math. J. 9 (1957), 119–221.Google Scholar
(11)Hochschild, G.Cohomology of algebraic linear groups. III. J. Math. 5 (1961), 492–519.Google Scholar
(12)Humphreys, J. E. Ordinary and modular representations of Chevalley groups. Lecture Notes in Mathematics, no. 528 (Springer, Berlin, 1976).Google Scholar
(13)Jantzen, J. C.Darstellungen halbeinfacher Gruppen und ihrer Frobenius-Kerne. J. reine angew. Math. 317 (1980), 157–199.Google Scholar
(14)Lusztig, G. Some problems in the representation theory of finite Chevalley groups. Proc. Symp. Pure. Math. (To appear.)Google Scholar
(15)Sullivan, J. B.Frobenius operations on Hochschild cohomology. Amer. J. Math. 102 (1980), 765–780.CrossRefGoogle Scholar
(16)Takeuchi, M.A correspondence between Hopf ideals and sub-Hopf algebras. Manuscripta Math. 7 (1972), 251–270.CrossRefGoogle Scholar
(17)Yehia, S. El B. Extensions of simple modules for the universal Chevalley group and its parabolic subgroups. Ph.D. Thesis, Warwick, 1982.Google Scholar