Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-06T04:27:51.194Z Has data issue: false hasContentIssue false
  • English
  • Français

On the cohomology of the sporadic simple group J4

Published online by Cambridge University Press:  24 October 2008

David John Green
David John Green
Affiliation:
Institut für Experimentelle Mathematik, Universität GHS Essen, D-W-4300 Essen 12, Germany
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we calculate part of the integral cohomology ring of the sporadic simple group J4; this group has order 221.33.5.7. 113.23.29.31.37.43. More precisely, we obtain all of the cohomology ring except for the 2-primary part. As the cohomology has already been written down [9] at the primes which divide the group order only once, we concentrate here on the primes 3 and 11. In both of these cases the Sylow p-subgroups are extraspecial of order p3 and exponent p. We use the method which identifies the p-primary cohomology with the ring of stable classes in the cohomology of a Sylow p-subgroup. The stable classes are all invariant under the action of the Sylow p-normalizer; and some time is spent finding invariant classes in the cohomology ring of 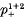, the extraspecial group. Section 2 studies the prime 11: the invariant classes are the stable classes, because the Sylow 11-subgroups have the Trivial Intersection (T.I.) property. In Section 3 we study the prime 3, and see that all conditions for invariant classes to be stable reduce to one condition.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 2 , March 1993 , pp. 253 - 266
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F.. Characters and cohomology of finite groups. Inst. Hautes Études Sci. Publ. Math. 9 (1961), 23–64.CrossRefGoogle Scholar
[2]Cartan, H. and Eilenberg, S.. Homological Algebra (Princeton University Press, 1956).Google Scholar
[3]Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A.. Atlas of Finite Groups (Oxford University Press, 1985).Google Scholar
[4]Janko, Z.. A new finite simple group of order 86·775·571·046·077·562·880 which possesses M 24 and the full covering group of M 22 as subgroups. J. Algebra 42 (1976), 564–596.CrossRefGoogle Scholar
[5]Kleidman, P. B. and Wilson, R. A.. The maximal subgroups of J 4. Proc. London Math. Soc. (3) 56 (1988), 484–510.CrossRefGoogle Scholar
[6]Leary, I. J.. The integral cohomology rings of some p-groups. Math. Proc. Cambridge Philos. Soc. 110 (1991), 25–32.CrossRefGoogle Scholar
[7]Lewis, G.. The integral cohomology rings of groups of order p3. Trans. Amer. Math. Soc. 132 (1968), 501–529.Google Scholar
[8]Norton, S. P.. The construction of J 4. Proc. Sympos. Pure Math. 37 (1980), 271–277.CrossRefGoogle Scholar
[9]Thomas, C. B.. Characteristic classes and 2-modular representations for some sporadic groups – II. In Algebraic Topology Poznań 1989, Lecture Notes in Math. vol. 1474 (Springer-Verlag, 1991), pp. 371–381.Google Scholar