The Parseval formulae for monotonic functions. III
Published online by Cambridge University Press: 24 October 2008
Extract
This sequence of papers is concerned with a group of theorems on Fourier transforms, and with the corresponding results for Fourier series. The transform theorems deal with the equations
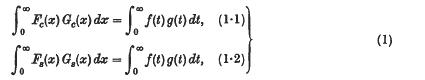
when two of the functions concerned are monotonic; and the series theorems, with the equations
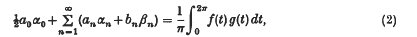
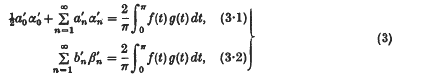
when two of the functions or sequences of coefficients are monotonic. A general survey of the problem was given in two earlier papers, which we shall call M.F. (I) and M.F. (II), and the results obtained were tabulated in M.F. (II). There is thus no need to restate the position in detail here. We shall merely recall as briefly as possible what has been proved already, so as to show the scope of the present paper.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 2 , April 1950 , pp. 249 - 267
- Copyright
- Copyright © Cambridge Philosophical Society 1950
References
* In (2), a n, b n are the Fourier coefficients of f in (0, 2π), and αn, βn are those of g. In (3), a′ n and b′n are the half-range cosine and sine coefficients of f in (0, π), and α′ n and β′ n are those of g.
† ‘The Pareeval formulae for monotonic functions. I’, Proc. Cambridge Phil. Soc. 43 (1947), 289–306Google Scholar; and ‘The Parseval formulae for monotonic functions. II’, Proc. Cambridge Phil. Soc. 46 (1950), 231–248.Google Scholar
‡ ‘On the Parseval formulae for Fourier transforms’, Proc. Cambridge Phil. Soc. 38 (1942), 1–19.Google Scholar
* ‘The Parseval formulae for monotonic functions. IV’.
† See Hardy, G. H. and Rogosinski, W. W., Fourier series (Cambridge, 1944), p. 25Google Scholar (for (IV) and (VI)), and p. 34 (for (VII)). For (V), see Zygmund, A., Trigonometrical series (Warsaw, 1935), p. 111Google Scholar; (VII) is given on pp. 109–10. The results (V) and (VII) are proved by partial summation, and (IV) and (VI) may be proved by partial integration.
‡ Here and elsewhere, we use the phrase’ b n decreases to zero’ as an abbreviation for’ b n decreases (for all values of n considered), and tends to zero as n → ∞’.
* We may use either the classical theorem on functions of the class L 2, or the theorem that (2) and (3) hold if f belongs to L and g is of bounded variation. Following the notation of M.F. (II), we shall refer to this latter theorem as (III).
* Hardy and Rogosinski, op. cit. p. 33.
† In Theorem 11 of M.F. (II), we had another instance in which the relaxation of a sign condition caused difficulty. The present case is quite different. In Theorem 11, we could extend our results easily to functions g which were bounded below; the difficulty arose over functions g tending to − ∞ as t → 2π. Here, the difficult case is that in which g is small and negative near the origin.
* Young, W. H., ‘On the Fourier series of bounded functions’, Proc. London Math. Soc. (2), 12 (1912), 41–70 (45)Google Scholar. The proof, which is well known, is given in Hobson, E. W., The theory of functions of a real variable, 2 (Cambridge, 1926), 619.Google Scholar
* These lemmas are quoted in footnotes on p. 260.
* See the discussion immediately after Theorem 19.
* Lemma 3 is as follows: If f(t) decreases to zero in (0, ∞), and if g(t) is any measurable function such that ![]() f(t) g(t) dt exists, then
f(t) g(t) dt exists, then
† These are of course defined by g +(x) = max (g(x), 0), g −(x) = min (g(x), 0), as in Theorem 17.
‡ Lemma 4 is given in M.F. (I), and is as follows: If f(t) decreases to zero in (0, ∞), and satisfies
and if
then
* In this case, the term given by n = π/x appears both in S 1 and in S 2; but as it is zero, this does not matter.
* See the forthcoming paper M.F. (IV).
* I.e. f either satisfies ![]() , or is convex.
, or is convex.
* See the paper referred to on p. 257. A number of theorems of this kind were proved by Young in this and other papers; but his standpoint was slightly different from that adopted here. As far as I know, he was concerned with conditions bearing directly on the functions themselves, and not with existence conditions on the integrals or series (except when he had already proved a summability theorem). Thus he gave the result quoted here, but I have not found Theorem 27, for instance, in his work.
* See M.F.(IV).
† We use square brackets to denote ‘integer part of’, as in Lemma 12; but we do not continue the practice of omitting these brackets in limits of summation, as this would be confusing here.
* As suggested in Zygmund, op. cit. p. 12; this method requires n to be an integer, but this is of course all we need here.
- 4
- Cited by




