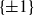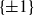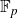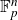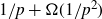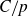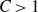1. Introduction
The irreducibility of random polynomials has attracted much interest in recent years. A well-known conjecture of Odlyzko and Poonen [
Reference Odlyzko and Poonen21
] is that the random polynomial
![]() $P(x) = x^{d} + b_{d-1}x^{d-1} + \dots + b_{1}x + b_{0}$
, where
$P(x) = x^{d} + b_{d-1}x^{d-1} + \dots + b_{1}x + b_{0}$
, where
![]() $b_{0} = 1$
and
$b_{0} = 1$
and
![]() $b_1,\dots, b_{d-1}$
are i.i.d.
$b_1,\dots, b_{d-1}$
are i.i.d.
![]() $\operatorname{Ber}(1/2)$
random variables (i.e. each
$\operatorname{Ber}(1/2)$
random variables (i.e. each
![]() $b_i$
is independently 0 or 1 with probability
$b_i$
is independently 0 or 1 with probability
![]() $1/2$
each), is irreducible in
$1/2$
each), is irreducible in
![]() $\mathbb{Z}[x]$
with probability
$\mathbb{Z}[x]$
with probability
![]() $1-o_d(1)$
. This was established in a more general form by Breuillard and Varjú [
Reference Breuillard and Varjú3
] under the Riemann Hypothesis for a family of Dedekind zeta functions. A version of this conjecture, where
$1-o_d(1)$
. This was established in a more general form by Breuillard and Varjú [
Reference Breuillard and Varjú3
] under the Riemann Hypothesis for a family of Dedekind zeta functions. A version of this conjecture, where
![]() $b_0,\dots, b_{d-1}$
are distributed uniformly in
$b_0,\dots, b_{d-1}$
are distributed uniformly in
![]() $\{1,\dots, L\}$
for L divisible by at least 4 distinct primes, was established (unconditionally) by Bary–Soroker and Kozma [
Reference Bary–Soroker and Kozma2
]. In recent work, Bary-Soroker, Koukoulopoulos, and Kozma [
Reference Bary–Soroker, Koukoulopoulos and Kozma1
] showed that the result continues to hold for
$\{1,\dots, L\}$
for L divisible by at least 4 distinct primes, was established (unconditionally) by Bary–Soroker and Kozma [
Reference Bary–Soroker and Kozma2
]. In recent work, Bary-Soroker, Koukoulopoulos, and Kozma [
Reference Bary–Soroker, Koukoulopoulos and Kozma1
] showed that the result continues to hold for
![]() $\{1,\dots, L\}$
for
$\{1,\dots, L\}$
for
![]() $L\geq 35$
. We refer the reader to [
Reference Bary–Soroker, Koukoulopoulos and Kozma1–Reference Breuillard and Varjú3
] for more precise and general versions of the aforementioned results.
$L\geq 35$
. We refer the reader to [
Reference Bary–Soroker, Koukoulopoulos and Kozma1–Reference Breuillard and Varjú3
] for more precise and general versions of the aforementioned results.
Another popular model of random polynomials is the characteristic polynomial of a random matrix. It was conjectured by Vu and Wood in 2009 and also by Babai (unpublished) in the 1970s [
Reference Vu25
] that for an
![]() $n\times n$
matrix
$n\times n$
matrix
![]() $N_n$
whose entries are i.i.d. Rademacher random variables (i.e.
$N_n$
whose entries are i.i.d. Rademacher random variables (i.e.
![]() $\pm 1$
with probability
$\pm 1$
with probability
![]() $1/2$
each), the characteristic polynomial
$1/2$
each), the characteristic polynomial
![]() $\widehat{\varphi}(t) = \det(tI_n-N_n)$
is irreducible with probability
$\widehat{\varphi}(t) = \det(tI_n-N_n)$
is irreducible with probability
![]() $1-o(1)$
. This was confirmed, under the extended Riemann Hypothesis, in recent work of Eberhard [
Reference Eberhard8
], building on [
Reference Breuillard and Varjú3
] and ideas from the non-asymptotic theory of random matrices. It is perhaps even more natural to consider the (real-rooted) characteristic polynomial
$1-o(1)$
. This was confirmed, under the extended Riemann Hypothesis, in recent work of Eberhard [
Reference Eberhard8
], building on [
Reference Breuillard and Varjú3
] and ideas from the non-asymptotic theory of random matrices. It is perhaps even more natural to consider the (real-rooted) characteristic polynomial
![]() $\varphi(t) = \det(tI_n - M_n)$
, where
$\varphi(t) = \det(tI_n - M_n)$
, where
![]() $M_n$
is an
$M_n$
is an
![]() $n\times n$
symmetric matrix whose entries on and above the diagonal are i.i.d. Rademacher random variables. In [
Reference Eberhard8
], Eberhard asked if
$n\times n$
symmetric matrix whose entries on and above the diagonal are i.i.d. Rademacher random variables. In [
Reference Eberhard8
], Eberhard asked if
![]() $\varphi(t)$
is irreducible with probability
$\varphi(t)$
is irreducible with probability
![]() $1-o(1)$
. We answer this question in the affirmative under the extended Riemann hypothesis.
$1-o(1)$
. We answer this question in the affirmative under the extended Riemann hypothesis.
Theorem 1·1. Assume the extended Riemann Hypothesis (ERH) (i.e., the Riemann Hypothesis for Dedekind zeta functions for all number fields). Then there is an absolute constant
![]() $c>0$
such that characteristic polynomial
$c>0$
such that characteristic polynomial
![]() $\varphi(t) = \det(tI_n - M_n)$
of an
$\varphi(t) = \det(tI_n - M_n)$
of an
![]() $n\times n$
random symmetric Rademacher matrix
$n\times n$
random symmetric Rademacher matrix
![]() $M_n$
is irreducible with probability at least
$M_n$
is irreducible with probability at least
![]() $1-2\exp(\!-cn^{1/4})$
.
$1-2\exp(\!-cn^{1/4})$
.
Remark. The proof in this paper can easily be extended to handle the class of
![]() $\alpha$
-balanced distributions considered in [
Reference Eberhard8
] with straightforward modifications; we leave the details to the interested reader.
$\alpha$
-balanced distributions considered in [
Reference Eberhard8
] with straightforward modifications; we leave the details to the interested reader.
It was noted in [
Reference Eberhard8
] that given the techniques in [
Reference Breuillard and Varjú3, Reference Eberhard8
], Theorem 1·1 (with the weaker probability bound
![]() $1-o(1)$
) can be deduced from the following universality statement: the probability that
$1-o(1)$
) can be deduced from the following universality statement: the probability that
![]() $tI_n - M_{n}$
is invertible over
$tI_n - M_{n}$
is invertible over
![]() $\mathbb{F}_p$
, for
$\mathbb{F}_p$
, for
![]() $p = n^{\Omega(1)}$
, is essentially the same as for an
$p = n^{\Omega(1)}$
, is essentially the same as for an
![]() $n\times n$
symmetric matrix whose entries on and above the diagonal are sampled from the uniform distribution on
$n\times n$
symmetric matrix whose entries on and above the diagonal are sampled from the uniform distribution on
![]() $\mathbb{F}_p$
. Despite the intensive efforts to study the singularity probability of symmetric Rademacher matrices ([
Reference Campos, Jenssen, Michelen and Sahasrabudhe4, Reference Campos, Mattos, Morris and Morrison6, Reference Costello, Tao and Vu7, Reference Ferber and Jain10, Reference Jain, Sah and Sawhney14, Reference Nguyen and Vu20, Reference Vershynin24
] and especially the recent breakthrough [
Reference Campos, Jenssen, Michelen and Sahasrabudhe5
] which confirms the long-standing conjecture that the singularity probability of symmetric Rademacher matrices is exponentially small), a result of this precision has remained elusive. While for
$\mathbb{F}_p$
. Despite the intensive efforts to study the singularity probability of symmetric Rademacher matrices ([
Reference Campos, Jenssen, Michelen and Sahasrabudhe4, Reference Campos, Mattos, Morris and Morrison6, Reference Costello, Tao and Vu7, Reference Ferber and Jain10, Reference Jain, Sah and Sawhney14, Reference Nguyen and Vu20, Reference Vershynin24
] and especially the recent breakthrough [
Reference Campos, Jenssen, Michelen and Sahasrabudhe5
] which confirms the long-standing conjecture that the singularity probability of symmetric Rademacher matrices is exponentially small), a result of this precision has remained elusive. While for
![]() $p = o(n^{1/8})$
, such a result is known due to work of Maples [
Reference Maples18
], the bound on p is too restrictive to imply Theorem 1·1 (even with the weaker probability
$p = o(n^{1/8})$
, such a result is known due to work of Maples [
Reference Maples18
], the bound on p is too restrictive to imply Theorem 1·1 (even with the weaker probability
![]() $1-o(1)$
). The main challenge in addressing the regime
$1-o(1)$
). The main challenge in addressing the regime
![]() $p = \omega(n^{1/2})$
is that one must consider the arithmetic structure of vectors which are orthogonal to random subspaces of small co-dimension. However, inverse Littlewood–Offord-type theorems (cf. [
Reference Ferber, Jain, Luh and Samotij11, Reference Rudelson and Vershynin22, Reference Tao and Vu23
]), which have been designed to study only arithmetically structured vectors, fail to apply to vectors in
$p = \omega(n^{1/2})$
is that one must consider the arithmetic structure of vectors which are orthogonal to random subspaces of small co-dimension. However, inverse Littlewood–Offord-type theorems (cf. [
Reference Ferber, Jain, Luh and Samotij11, Reference Rudelson and Vershynin22, Reference Tao and Vu23
]), which have been designed to study only arithmetically structured vectors, fail to apply to vectors in
![]() $\mathbb{F}_{p}$
with anticoncentration at least
$\mathbb{F}_{p}$
with anticoncentration at least
![]() $C/p$
for some large constant
$C/p$
for some large constant
![]() $C > 1$
. While consideration of vectors with anticoncentration at most
$C > 1$
. While consideration of vectors with anticoncentration at most
![]() $C/p$
is inessential for the less precise results mentioned above, here we must provide an appropriate structural result for vectors with anticoncentration at least
$C/p$
is inessential for the less precise results mentioned above, here we must provide an appropriate structural result for vectors with anticoncentration at least
![]() $1/p + \Omega(1/p^2)$
, say. This is accomplished in the key Proposition 2·5. Finally, we note that an upper bound on the singularity probability of the form
$1/p + \Omega(1/p^2)$
, say. This is accomplished in the key Proposition 2·5. Finally, we note that an upper bound on the singularity probability of the form
![]() $1/p + O(1/p^2)$
can be deduced for
$1/p + O(1/p^2)$
can be deduced for
![]() $p=o(n^{1/2})$
from estimates on the expected size of the kernel over
$p=o(n^{1/2})$
from estimates on the expected size of the kernel over
![]() $\mathbb{F}_p$
due to [
Reference Ferber9
], but for similar reasons to those mentioned above these estimates do not appear to extend to p which is larger than a small polynomial.
$\mathbb{F}_p$
due to [
Reference Ferber9
], but for similar reasons to those mentioned above these estimates do not appear to extend to p which is larger than a small polynomial.
An obvious generalisation of studying the probability of singularity of
![]() $M_n$
over
$M_n$
over
![]() $\mathbb{F}_p$
is studying the rank distribution of
$\mathbb{F}_p$
is studying the rank distribution of
![]() $M_n$
over
$M_n$
over
![]() $\mathbb{F}_p$
. For symmetric Rademacher matrices, the only prior work we are aware of is the aforementioned work of Maples [
Reference Maples18
], which effectively requires
$\mathbb{F}_p$
. For symmetric Rademacher matrices, the only prior work we are aware of is the aforementioned work of Maples [
Reference Maples18
], which effectively requires
![]() $p = o(n^{1/8})$
. Results for unrestricted p are available under the very strong assumption that the independent entries of
$p = o(n^{1/8})$
. Results for unrestricted p are available under the very strong assumption that the independent entries of
![]() $M_n$
are uniformly [
Reference Fulman and Goldstein12
] or nearly-uniformly [
Reference Koenig and Nguyen15
] distributed over
$M_n$
are uniformly [
Reference Fulman and Goldstein12
] or nearly-uniformly [
Reference Koenig and Nguyen15
] distributed over
![]() $\mathbb{F}_p$
.
$\mathbb{F}_p$
.
The main innovation of our work is the following result regarding the rank distribution of symmetric Rademacher matrices (and diagonal perturbations) over
![]() $\mathbb{F}_p$
for all
$\mathbb{F}_p$
for all
![]() $2 < p \leq \exp(\eta n^{1/4})$
:
$2 < p \leq \exp(\eta n^{1/4})$
:
Theorem 1·2. There exists
![]() $\eta > 0$
so that for any
$\eta > 0$
so that for any
![]() $2 < p\le\exp(\eta n^{1/4})$
and for any
$2 < p\le\exp(\eta n^{1/4})$
and for any
![]() $\lambda\in\mathbb{F}_p$
, the
$\lambda\in\mathbb{F}_p$
, the
![]() $n\times n$
symmetric Rademacher matrix
$n\times n$
symmetric Rademacher matrix
![]() $M_n$
satisfies
$M_n$
satisfies
Remark. The proof can be extended routinely to the class of
![]() $\alpha$
-balanced distributions; however, for the sake of brevity, we have restricted our attention to the Rademacher distribution.
$\alpha$
-balanced distributions; however, for the sake of brevity, we have restricted our attention to the Rademacher distribution.
Remark. Theorem 1·2 is the natural symmetric analog of the results in [ Reference Luh, Meehan and Nguyen16, Reference Maples17 ]. As mentioned above, a version was known for p sufficiently small (with weaker error terms) due to Maples [ Reference Maples18 ].
1·1. Organisation
The remainder of this paper is organised as follows. In Section 2, we prove our key structural result (Proposition 2·5) for vectors which are orthogonal to many rows of
![]() $M_n$
. In Section 3, we use this, along with arguments in [
Reference Koenig and Nguyen15, Reference Maples18
] to deduce Theorem 1·2. Appendix A contains the deduction of Theorem 1·1 from the
$M_n$
. In Section 3, we use this, along with arguments in [
Reference Koenig and Nguyen15, Reference Maples18
] to deduce Theorem 1·2. Appendix A contains the deduction of Theorem 1·1 from the
![]() $k=1$
case of Theorem 1·2, following the arguments in [
Reference Eberhard8
]. Finally, Appendix B contains the proof of a ‘crude’ structure theorem (which appears in [
Reference Ferber and Jain10
], but with worse parameters) for the reader’s convenience.
$k=1$
case of Theorem 1·2, following the arguments in [
Reference Eberhard8
]. Finally, Appendix B contains the proof of a ‘crude’ structure theorem (which appears in [
Reference Ferber and Jain10
], but with worse parameters) for the reader’s convenience.
1·2. Notation
We write
![]() $B_2^d(R)$
for the radius R Euclidean ball in
$B_2^d(R)$
for the radius R Euclidean ball in
![]() $\mathbb{R}^d$
. For vectors
$\mathbb{R}^d$
. For vectors
![]() $\boldsymbol{b},\boldsymbol{a}$
, we write
$\boldsymbol{b},\boldsymbol{a}$
, we write
![]() $\boldsymbol{b}\subseteq\boldsymbol{a}$
if there is a subset S of coordinates such that the restriction
$\boldsymbol{b}\subseteq\boldsymbol{a}$
if there is a subset S of coordinates such that the restriction
![]() $\boldsymbol{a}|_S$
is identified with
$\boldsymbol{a}|_S$
is identified with
![]() $\boldsymbol{b}$
. As is typical, we write
$\boldsymbol{b}$
. As is typical, we write
![]() $f = O(g)$
to mean
$f = O(g)$
to mean
![]() $|f|\le Cg$
for some sufficiently large constant C, and
$|f|\le Cg$
for some sufficiently large constant C, and
![]() $f = \Omega(g)$
to mean
$f = \Omega(g)$
to mean
![]() $f\ge c|g|$
for some sufficiently small constant
$f\ge c|g|$
for some sufficiently small constant
![]() $c > 0$
.
$c > 0$
.
2. Structure Theorem for Almost-Kernel Vectors
We begin by showing the easy fact that, except with exponentially small probability, no sparse vector has sparse image under M.
Definition 2·1. Let
![]() $0 \leq r \leq n$
be a parameter. We say that
$0 \leq r \leq n$
be a parameter. We say that
![]() $\boldsymbol{v}\in\mathbb{F}_p^n$
is an r-kernel vector of a matrix
$\boldsymbol{v}\in\mathbb{F}_p^n$
is an r-kernel vector of a matrix
![]() $M\in\mathbb{F}_p^{n\times n}$
if
$M\in\mathbb{F}_p^{n\times n}$
if
![]() $M\boldsymbol{v}$
is r-sparse, i.e., has at most r nonzero entries.
$M\boldsymbol{v}$
is r-sparse, i.e., has at most r nonzero entries.
In particular, 0-kernel vectors correspond to the usual right-kernel of M.
Lemma 2·2. Let
![]() $p \ge 3$
. With probability at least
$p \ge 3$
. With probability at least
![]() $1 - \exp(\!-n/6)$
, the symmetric random matrix
$1 - \exp(\!-n/6)$
, the symmetric random matrix
![]() $M_n - \lambda I_n$
has no nonzero
$M_n - \lambda I_n$
has no nonzero
![]() $n/(16\log p)$
-sparse
$n/(16\log p)$
-sparse
![]() $n/4$
-kernel vectors in
$n/4$
-kernel vectors in
![]() $\mathbb{F}_p^n$
.
$\mathbb{F}_p^n$
.
Proof. Fix a nonzero
![]() $\boldsymbol{v} \in \mathbb{F}_p^n$
with
$\boldsymbol{v} \in \mathbb{F}_p^n$
with
![]() $v_1 \neq 0$
. We begin by computing the probability that
$v_1 \neq 0$
. We begin by computing the probability that
![]() $M\boldsymbol{v}$
is
$M\boldsymbol{v}$
is
![]() $n/4$
-sparse. We denote the rows of M by
$n/4$
-sparse. We denote the rows of M by
![]() $R_1,\dots, R_n$
and reveal the rows from bottom-to-top. Since the first entry
$R_1,\dots, R_n$
and reveal the rows from bottom-to-top. Since the first entry
![]() $R_i$
is independent
$R_i$
is independent
![]() $R_{i+1},\dots, R_n$
, since
$R_{i+1},\dots, R_n$
, since
![]() $v_1 \neq 0$
, and since
$v_1 \neq 0$
, and since
![]() $p\geq 3$
, it follows that
$p\geq 3$
, it follows that
Therefore, the probability that
![]() $M\boldsymbol{v}$
is
$M\boldsymbol{v}$
is
![]() $n/4$
-sparse is at most
$n/4$
-sparse is at most
Finally, taking the union bound over the at most
choices of
![]() $n/(16\log{p})$
-sparse vectors in
$n/(16\log{p})$
-sparse vectors in
![]() $\mathbb{F}_{p}^{n}$
gives the desired conclusion.
$\mathbb{F}_{p}^{n}$
gives the desired conclusion.
We recall the definition of the atom probability of a vector
![]() $\boldsymbol{v} \in \mathbb{F}_{p}^{n}$
with respect to Rademacher random variables.
$\boldsymbol{v} \in \mathbb{F}_{p}^{n}$
with respect to Rademacher random variables.
Definition 2·3. The atom probability of a vector
![]() $\boldsymbol{v} \in \mathbb{F}_{p}^{n}$
is defined as
$\boldsymbol{v} \in \mathbb{F}_{p}^{n}$
is defined as
where
![]() $\xi_1,\dots, \xi_n$
are i.i.d. Rademacher random variables.
$\xi_1,\dots, \xi_n$
are i.i.d. Rademacher random variables.
We will need the following ‘crude’ structure theorem for
![]() $(n-n/\log p)$
-kernel vectors, which follows from a more careful version of the argument in [
Reference Ferber and Jain10
]. For the reader’s convenience, we include details in Appendix B.
$(n-n/\log p)$
-kernel vectors, which follows from a more careful version of the argument in [
Reference Ferber and Jain10
]. For the reader’s convenience, we include details in Appendix B.
Proposition 2·4. Suppose that
![]() $2 < p\le\exp(c_{2.4}n^{1/4})$
and fix
$2 < p\le\exp(c_{2.4}n^{1/4})$
and fix
![]() $\lambda\in\mathbb{F}_p$
. With probability at least
$\lambda\in\mathbb{F}_p$
. With probability at least
![]() $1-\exp(\!-n/8)$
, every nonzero vector
$1-\exp(\!-n/8)$
, every nonzero vector
![]() $\boldsymbol{v} \in \mathbb{F}_p^{n}$
which is orthogonal to at least
$\boldsymbol{v} \in \mathbb{F}_p^{n}$
which is orthogonal to at least
![]() $n-n/\log p$
rows of the random symmetric matrix
$n-n/\log p$
rows of the random symmetric matrix
![]() $M_n-\lambda I_n$
over
$M_n-\lambda I_n$
over
![]() $\mathbb{F}_p$
satisfies the following two properties:
$\mathbb{F}_p$
satisfies the following two properties:
-
(i)
 $|\operatorname{supp}\!(\boldsymbol{v})| \geq n/(16\log{p})$
, and
$|\operatorname{supp}\!(\boldsymbol{v})| \geq n/(16\log{p})$
, and -
(ii) there exists
 $S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
with
$S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
with
 $|S| \in [\sqrt{n\log n},n^{3/4}]$
such that
$|S| \in [\sqrt{n\log n},n^{3/4}]$
such that  \begin{equation*}\rho_{\mathbb{F}_p}(\boldsymbol{v}|_S)\le\frac{C_{2.4}}{p}.\end{equation*}
\begin{equation*}\rho_{\mathbb{F}_p}(\boldsymbol{v}|_S)\le\frac{C_{2.4}}{p}.\end{equation*}
Since
for any
![]() $S\subseteq [n]$
, the crude structure theorem shows that any
$S\subseteq [n]$
, the crude structure theorem shows that any
![]() $(n/\log p)$
-kernel vector of
$(n/\log p)$
-kernel vector of
![]() $M_n - \lambda I_n$
has atom probability at most
$M_n - \lambda I_n$
has atom probability at most
![]() $\dfrac{C_{2.4}}{p}$
. While this result is optimal up to the constant
$\dfrac{C_{2.4}}{p}$
. While this result is optimal up to the constant
![]() $C_{2.4}$
, it is unfortunately insufficient for our application. The next proposition, which is one of the main innovations of this paper, allows us to show that any
$C_{2.4}$
, it is unfortunately insufficient for our application. The next proposition, which is one of the main innovations of this paper, allows us to show that any
![]() $(n/\log p)$
-kernel vector of
$(n/\log p)$
-kernel vector of
![]() $M_{n}-\lambda I_n$
has many disjoint chunks with atom-probability approximately
$M_{n}-\lambda I_n$
has many disjoint chunks with atom-probability approximately
![]() $1/p$
.
$1/p$
.
Proposition 2·5. Suppose that
![]() $2 < p\le\exp(c_{2.5}n^{1/4})$
and fix
$2 < p\le\exp(c_{2.5}n^{1/4})$
and fix
![]() $\lambda\in\mathbb{F}_p$
. Let
$\lambda\in\mathbb{F}_p$
. Let
![]() $m = C_{2.5}\log p$
. With probability at least
$m = C_{2.5}\log p$
. With probability at least
![]() $1-\exp(\!-n/9)$
, every vector
$1-\exp(\!-n/9)$
, every vector
![]() $\boldsymbol{v}$
orthogonal to at least
$\boldsymbol{v}$
orthogonal to at least
![]() $n-n/\log p$
rows of the random symmetric matrix
$n-n/\log p$
rows of the random symmetric matrix
![]() $M_n-\lambda I_n$
over
$M_n-\lambda I_n$
over
![]() $\mathbb{F}_p$
has the following property, which we denote by (
$\mathbb{F}_p$
has the following property, which we denote by (
![]() $\dagger$
): given any set
$\dagger$
): given any set
![]() $T\subseteq[n]$
of size
$T\subseteq[n]$
of size
![]() $n/4$
, there at least
$n/4$
, there at least
![]() $n/(2m)$
disjoint sets S of size m in
$n/(2m)$
disjoint sets S of size m in
![]() $[n]\setminus T$
such that
$[n]\setminus T$
such that
Proof. This is trivial for
![]() $p\le C_{2.5}^{1/2}$
, so assume the opposite. Let
$p\le C_{2.5}^{1/2}$
, so assume the opposite. Let
![]() $r = n/\log p$
.
$r = n/\log p$
.
First, by Lemma 2·2 and Proposition 2·4, we may assume that
![]() $\boldsymbol{v}$
has some
$\boldsymbol{v}$
has some
![]() $S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
with
$S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
with
![]() $|S|\in [\sqrt{n\log n},n^{3/4}]$
such that
$|S|\in [\sqrt{n\log n},n^{3/4}]$
such that
For some fixed vector with this property, a straightforward argument (cf. proof of Proposition 2·4) shows that the probability that it is orthogonal to some set of
![]() $n-r$
rows of
$n-r$
rows of
![]() $M_n$
is at most
$M_n$
is at most
 \begin{equation}\binom{n}{r}\cdot\bigg(\frac{C_{2\cdot4}}{p}\bigg)^{n-n^{3/4}-r}\le C^np^{-n}.\end{equation}
\begin{equation}\binom{n}{r}\cdot\bigg(\frac{C_{2\cdot4}}{p}\bigg)^{n-n^{3/4}-r}\le C^np^{-n}.\end{equation}
We will use a union bound argument to establish Proposition 2·5. Given (2·1), the key is to show that the set of vectors
![]() $\boldsymbol{v}$
which fail to satisfy (
$\boldsymbol{v}$
which fail to satisfy (
![]() $\dagger$
) is sufficiently sparse in
$\dagger$
) is sufficiently sparse in
![]() $\mathbb{F}_p^n$
. To this end, consider some T of size
$\mathbb{F}_p^n$
. To this end, consider some T of size
![]() $n/4$
and for each such T, consider a fixed (but otherwise arbitrary) partition of
$n/4$
and for each such T, consider a fixed (but otherwise arbitrary) partition of
![]() $[n]\setminus T$
into
$[n]\setminus T$
into
![]() $S_1,\ldots,S_{3n/(4m)}$
of size m (up to rounding). There are at most
$S_1,\ldots,S_{3n/(4m)}$
of size m (up to rounding). There are at most
![]() $2^n$
ways to choose T and at most
$2^n$
ways to choose T and at most
![]() $2^n$
ways to choose which of these sets satisfy
$2^n$
ways to choose which of these sets satisfy
If
![]() $\boldsymbol{v}$
violates (
$\boldsymbol{v}$
violates (
![]() $\dagger$
), then at least a third of these indices are failures. Thus, we see that the number of vectors which violate (
$\dagger$
), then at least a third of these indices are failures. Thus, we see that the number of vectors which violate (
![]() $\dagger$
) is at most
$\dagger$
) is at most
where U is the set of
![]() $\mathbb{F}_p$
-vectors of size m with
$\mathbb{F}_p$
-vectors of size m with
Fix some sufficiently large absolute constant
![]() $C' > 0$
(depending on C in (2·1)). We claim that if
$C' > 0$
(depending on C in (2·1)). We claim that if
![]() $C_{2.5}\ge 1$
chosen large enough, then
$C_{2.5}\ge 1$
chosen large enough, then
![]() $|U|\le(p/C')^m$
$|U|\le(p/C')^m$
![]() $\Big(\textrm{recall that}\ p > C_{2.5}^{1/2}\Big)$
. Note that this claim, together with (2·1) and (2·2) completes the proof of Proposition 2·5.
$\Big(\textrm{recall that}\ p > C_{2.5}^{1/2}\Big)$
. Note that this claim, together with (2·1) and (2·2) completes the proof of Proposition 2·5.
We now prove the claim. Note that if
![]() $\boldsymbol{b} = (b_1,\ldots,b_m)\in U\subseteq\mathbb{F}_p^m$
for i.i.d. Rademacher random variables
$\boldsymbol{b} = (b_1,\ldots,b_m)\in U\subseteq\mathbb{F}_p^m$
for i.i.d. Rademacher random variables
![]() $\xi_1,\dots, \xi_n$
we have that
$\xi_1,\dots, \xi_n$
we have that
 \begin{align*}\frac{1}{p^2} < \operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{b}) &= \sup_{x\in\mathbb{F}_p}\bigg|\mathbb{P}_\xi[b_1\xi_1+\cdots+b_m\xi_m=x]-\frac{1}{p}\bigg|\\&= \sup_{x\in\mathbb{F}_p}\bigg|\frac{1}{p}\sum_{\ell\in\mathbb{F}_p^\times}\exp\!(2\pi i(\ell x/p))\prod_{j=1}^m\cos\!(2\pi(\ell b_j/p))\bigg|\\&\le\frac{1}{p}\sum_{\ell\in\mathbb{F}_p^\times}\prod_{j=1}^m|\cos\!(2\pi(\ell b_j/p))|\\&\le\frac{1}{p}\sum_{\ell\in\mathbb{F}_p^\times}\exp\!\bigg(\!-\sum_{j=1}^m\lVert{2\ell b_j/p}\rVert_{\mathbb{R}/\mathbb{Z}}^2\bigg)\\&\le\max_{\ell\in\mathbb{F}_p^\times}\exp\!\bigg(\!-\sum_{j=1}^m\lVert{\ell b_j/p}\rVert_{\mathbb{R}/\mathbb{Z}}^2\bigg).\end{align*}
\begin{align*}\frac{1}{p^2} < \operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{b}) &= \sup_{x\in\mathbb{F}_p}\bigg|\mathbb{P}_\xi[b_1\xi_1+\cdots+b_m\xi_m=x]-\frac{1}{p}\bigg|\\&= \sup_{x\in\mathbb{F}_p}\bigg|\frac{1}{p}\sum_{\ell\in\mathbb{F}_p^\times}\exp\!(2\pi i(\ell x/p))\prod_{j=1}^m\cos\!(2\pi(\ell b_j/p))\bigg|\\&\le\frac{1}{p}\sum_{\ell\in\mathbb{F}_p^\times}\prod_{j=1}^m|\cos\!(2\pi(\ell b_j/p))|\\&\le\frac{1}{p}\sum_{\ell\in\mathbb{F}_p^\times}\exp\!\bigg(\!-\sum_{j=1}^m\lVert{2\ell b_j/p}\rVert_{\mathbb{R}/\mathbb{Z}}^2\bigg)\\&\le\max_{\ell\in\mathbb{F}_p^\times}\exp\!\bigg(\!-\sum_{j=1}^m\lVert{\ell b_j/p}\rVert_{\mathbb{R}/\mathbb{Z}}^2\bigg).\end{align*}
In particular, there is some
![]() $\ell\in\mathbb{F}_p^\times$
with
$\ell\in\mathbb{F}_p^\times$
with
 \begin{equation*}\sum_{j=1}^m\lVert{\ell b_j/p}\rVert_{\mathbb{R}/\mathbb{Z}}^2\le 2\log p.\end{equation*}
\begin{equation*}\sum_{j=1}^m\lVert{\ell b_j/p}\rVert_{\mathbb{R}/\mathbb{Z}}^2\le 2\log p.\end{equation*}
To count the number of such vectors, note that there are at most p choices of
![]() $\ell$
. Moreover, since coordinate-wise multiplication by
$\ell$
. Moreover, since coordinate-wise multiplication by
![]() $\ell$
is a bijection from
$\ell$
is a bijection from
![]() $\mathbb{F}_{p}^{m}$
onto itself, it follows that
$\mathbb{F}_{p}^{m}$
onto itself, it follows that
 \begin{equation*}|U| \leq p\cdot\#\{\boldsymbol{b}\in \mathbb{F}_p^m \;:\; \sum_{j=1}^{m}\|b_j/p\|^{2}_{\mathbb{R}/\mathbb{Z}} \leq 2\log{p}\}.\end{equation*}
\begin{equation*}|U| \leq p\cdot\#\{\boldsymbol{b}\in \mathbb{F}_p^m \;:\; \sum_{j=1}^{m}\|b_j/p\|^{2}_{\mathbb{R}/\mathbb{Z}} \leq 2\log{p}\}.\end{equation*}
The second term in the product is a count of lattice points in a ball. A standard volumetric argument shows that there are at most
![]() $\operatorname{vol}(B_2^m(R+\sqrt{m}))$
integer lattice points in an m-dimensional ball of radius R. Hence, since
$\operatorname{vol}(B_2^m(R+\sqrt{m}))$
integer lattice points in an m-dimensional ball of radius R. Hence, since
![]() $\operatorname{vol}(B_2^m(1))\le A^mm^{-m/2}$
for some absolute constant A we see that
$\operatorname{vol}(B_2^m(1))\le A^mm^{-m/2}$
for some absolute constant A we see that
since
![]() $m = C_{2.5}\log{p}$
and
$m = C_{2.5}\log{p}$
and
![]() $p > C_{2.5}^{1/2}$
. Choosing
$p > C_{2.5}^{1/2}$
. Choosing
![]() $C_{2.5}$
sufficiently large completes the proof.
$C_{2.5}$
sufficiently large completes the proof.
3. Proof of Theorem 1·2
We are now in position to deduce Theorem 1·2; the high-level structure of the argument is as in [ Reference Koenig and Nguyen15, Reference Maples18 ]. However, we make explicit a number of details which are implicit in [ Reference Maples18 ] as well as make a number of simplifications and changes to account for use of our structure theorem Proposition 2·5.
We first recall a basic linear algebra fact about full-rank principal minors.
Lemma 3·1. If
![]() $M\in\mathbb{F}^{n\times n}$
is a symmetric matrix of rank r, then there is an invertible
$M\in\mathbb{F}^{n\times n}$
is a symmetric matrix of rank r, then there is an invertible
![]() $r\times r$
principal minor of M.
$r\times r$
principal minor of M.
Fix
![]() $\lambda\in\mathbb{F}_p$
. We consider the nested sequence of symmetric matrices
$\lambda\in\mathbb{F}_p$
. We consider the nested sequence of symmetric matrices
where
![]() $M_{i} - \lambda I_{i}$
is the top-left
$M_{i} - \lambda I_{i}$
is the top-left
![]() $i\times i$
-submatrix of
$i\times i$
-submatrix of
![]() $M - \lambda I$
(hence, the nested sequence is obtained by iteratively adding symmetric “reverse-L” shapes of Rademacher random variables, with a shift by
$M - \lambda I$
(hence, the nested sequence is obtained by iteratively adding symmetric “reverse-L” shapes of Rademacher random variables, with a shift by
![]() $\lambda$
on the diagonal element). For simplicity, let
$\lambda$
on the diagonal element). For simplicity, let
![]() $A_t = M_t - \lambda I_t$
. Define the events
$A_t = M_t - \lambda I_t$
. Define the events
where recall that (
![]() $\dagger$
) is the property that given any set
$\dagger$
) is the property that given any set
![]() $T\subseteq[t]$
of size
$T\subseteq[t]$
of size
![]() $t/4$
, there at least
$t/4$
, there at least
![]() $t/(2m)$
disjoint sets S of size
$t/(2m)$
disjoint sets S of size
![]() $m = C_{2.5}\log{p}$
in
$m = C_{2.5}\log{p}$
in
![]() $[t]\setminus T$
such that
$[t]\setminus T$
such that
By Lemma 2·2 and Proposition 2·5, we see that
Lemma 3·2. We have for
![]() $2 < p\le\exp(c_{3.2}n^{1/4})$
, fixed
$2 < p\le\exp(c_{3.2}n^{1/4})$
, fixed
![]() $\lambda\in\mathbb{F}_p$
, and for any
$\lambda\in\mathbb{F}_p$
, and for any
![]() $k\ge 0$
that
$k\ge 0$
that
 \begin{align*}\mathbb{P}[\!\operatorname{corank}A_{t+1} = k-1|A_{t} \;:\; \operatorname{corank}A_t=k\wedge\mathcal{E}_{S,t}\wedge\mathcal{E}_{U,t}] &= 1 - p^{-k} + O(\!\exp(\!-\Omega(t))),\\\!\!\!\!\!\!\!\mathbb{P}[\!\operatorname{corank}A_{t+1} = k + 0|A_{t} \;:\; \operatorname{corank}A_t=k\wedge\mathcal{E}_{S,t}\wedge\mathcal{E}_{U,t}] & \\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= p^{-k}-p^{-k-1}+ O(\!\exp(\!-\Omega(t/\log p))),\\\mathbb{P}[\!\operatorname{corank}A_{t+1} = k+1|A_{t}\; :\; \operatorname{corank}A_t=k\wedge\mathcal{E}_{S,t}\wedge\mathcal{E}_{U,t}] &= p^{-k-1} + O(\!\exp(\!-\Omega(t/\log p))).\end{align*}
\begin{align*}\mathbb{P}[\!\operatorname{corank}A_{t+1} = k-1|A_{t} \;:\; \operatorname{corank}A_t=k\wedge\mathcal{E}_{S,t}\wedge\mathcal{E}_{U,t}] &= 1 - p^{-k} + O(\!\exp(\!-\Omega(t))),\\\!\!\!\!\!\!\!\mathbb{P}[\!\operatorname{corank}A_{t+1} = k + 0|A_{t} \;:\; \operatorname{corank}A_t=k\wedge\mathcal{E}_{S,t}\wedge\mathcal{E}_{U,t}] & \\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= p^{-k}-p^{-k-1}+ O(\!\exp(\!-\Omega(t/\log p))),\\\mathbb{P}[\!\operatorname{corank}A_{t+1} = k+1|A_{t}\; :\; \operatorname{corank}A_t=k\wedge\mathcal{E}_{S,t}\wedge\mathcal{E}_{U,t}] &= p^{-k-1} + O(\!\exp(\!-\Omega(t/\log p))).\end{align*}
Remark. Note that, without the error terms inside
![]() $O(\!{\cdot}\!)$
, the probabilities are exactly the same as for the uniform model (i.e. the independent entries of
$O(\!{\cdot}\!)$
, the probabilities are exactly the same as for the uniform model (i.e. the independent entries of
![]() $M_n$
are chosen uniformly from
$M_n$
are chosen uniformly from
![]() $\mathbb{F}_p$
).
$\mathbb{F}_p$
).
Before proving Lemma 3·2, let us show how it implies Theorem 1·2.
Proof of Theorem 1·2. We consider the exposure process obtained by iteratively revealing
![]() $M_t$
for
$M_t$
for
![]() $1\le t\le n$
and considering the resulting corank of
$1\le t\le n$
and considering the resulting corank of
![]() $A_t$
. Starting from a random
$A_t$
. Starting from a random
![]() $A_{n/20}$
, let
$A_{n/20}$
, let
![]() $\tau$
denote the (random) first value of
$\tau$
denote the (random) first value of
![]() $t\geq n/20$
such that either (i)
$t\geq n/20$
such that either (i)
![]() $A_{t} \in \mathcal{E}_{S,t}^{c} \cup \mathcal{E}_{U,t}^{c}$
, or (ii)
$A_{t} \in \mathcal{E}_{S,t}^{c} \cup \mathcal{E}_{U,t}^{c}$
, or (ii)
![]() $\operatorname{corank}(A_t) = 0$
. We claim that, except with probability at most
$\operatorname{corank}(A_t) = 0$
. We claim that, except with probability at most
![]() $O(\!\exp(\!-\Omega(n/\log{p})))$
, we have
$O(\!\exp(\!-\Omega(n/\log{p})))$
, we have
![]() $\tau \leq n/2$
, and moreover,
$\tau \leq n/2$
, and moreover,
![]() $A_{\tau}$
satisfies condition (ii) and not condition (i).
$A_{\tau}$
satisfies condition (ii) and not condition (i).
To see this, note that by Lemma 2·2 and Proposition 2·5, the probability that
![]() $A_{t} \in \mathcal{E}_{S,t}^{c} \cup \mathcal{E}_{U,t}^{c}$
is
$A_{t} \in \mathcal{E}_{S,t}^{c} \cup \mathcal{E}_{U,t}^{c}$
is
![]() $O(\!\exp(\!-\Omega(n)))$
for any
$O(\!\exp(\!-\Omega(n)))$
for any
![]() $t\geq n/20$
. Moreover, for
$t\geq n/20$
. Moreover, for
![]() $A_{t} \in \mathcal{E}_{S,t} \wedge \mathcal{E}_{U,t}$
with
$A_{t} \in \mathcal{E}_{S,t} \wedge \mathcal{E}_{U,t}$
with
![]() $\operatorname{corank}(A_{t}) = k \geq 1$
, we see that
$\operatorname{corank}(A_{t}) = k \geq 1$
, we see that
![]() $\mathbb{P}[\operatorname{corank}A_{t+1} = k-1 \mid A_{t}] \geq 1-{1}/{3} + O(\!\exp(\!-\Omega(n))) \geq {3}/{5}$
for all n sufficiently large, and similarly,
$\mathbb{P}[\operatorname{corank}A_{t+1} = k-1 \mid A_{t}] \geq 1-{1}/{3} + O(\!\exp(\!-\Omega(n))) \geq {3}/{5}$
for all n sufficiently large, and similarly,
![]() $\mathbb{P}[\!\operatorname{corank}A_{t+1} = k+1 \mid A_{t}] \leq {1}/{8}$
for all n sufficiently large. Therefore, by a straightforward comparison argument, it follows that for all n sufficiently large, the probability that
$\mathbb{P}[\!\operatorname{corank}A_{t+1} = k+1 \mid A_{t}] \leq {1}/{8}$
for all n sufficiently large. Therefore, by a straightforward comparison argument, it follows that for all n sufficiently large, the probability that
![]() $\tau \leq n/2$
and
$\tau \leq n/2$
and
![]() $A_{\tau}$
satisfies condition (ii) and not condition (i) is at most
$A_{\tau}$
satisfies condition (ii) and not condition (i) is at most
where
![]() $q = O(\!\exp(\!-\Omega(n)))$
is the probability that a biased random walk with steps
$q = O(\!\exp(\!-\Omega(n)))$
is the probability that a biased random walk with steps
![]() $-1$
with probability
$-1$
with probability
![]() $1/2$
, 0 with probability
$1/2$
, 0 with probability
![]() $1/4$
, and
$1/4$
, and
![]() $+1$
with probability
$+1$
with probability
![]() $1/4$
and initial state
$1/4$
and initial state
![]() $n/20$
does not hit 0 in
$n/20$
does not hit 0 in
![]() $n/2 - n/20$
steps.
$n/2 - n/20$
steps.
To summarise, we have shown that except with probability
![]() $O(\!\exp(\!-\Omega(n/\log{p})))$
, there exists some
$O(\!\exp(\!-\Omega(n/\log{p})))$
, there exists some
![]() $\tau \in [n/20, n/2]$
such that
$\tau \in [n/20, n/2]$
such that
![]() $A_{\tau} \in \mathcal{E}_{S,\tau} \wedge \mathcal{E}_{U,\tau}$
and
$A_{\tau} \in \mathcal{E}_{S,\tau} \wedge \mathcal{E}_{U,\tau}$
and
![]() $\operatorname{corank}(A_{\tau}) = 0$
. From this point onwards, outside an event of probability at most
$\operatorname{corank}(A_{\tau}) = 0$
. From this point onwards, outside an event of probability at most
![]() $O(\!\exp(\!-\Omega(n/\log{p})))$
, it follows by the remark following Lemma 3·2 that we can couple the corank process
$O(\!\exp(\!-\Omega(n/\log{p})))$
, it follows by the remark following Lemma 3·2 that we can couple the corank process
![]() $A_{\tau+1},\dots, A_{n}$
with the corank process
$A_{\tau+1},\dots, A_{n}$
with the corank process
![]() $A^{\prime}_{1},\dots, A^{\prime}_{n-\tau}$
where
$A^{\prime}_{1},\dots, A^{\prime}_{n-\tau}$
where
![]() $A^{\prime}_{i}$
is the top-left
$A^{\prime}_{i}$
is the top-left
![]() $i\times i$
sub-matrix of
$i\times i$
sub-matrix of
![]() $M^{\prime}_{n-\tau} - \lambda$
and
$M^{\prime}_{n-\tau} - \lambda$
and
![]() $M^{\prime}_{n-\tau}$
is an
$M^{\prime}_{n-\tau}$
is an
![]() $(n-\tau) \times (n-\tau)$
random symmetric matrix whose independent entries are chosen uniformly from
$(n-\tau) \times (n-\tau)$
random symmetric matrix whose independent entries are chosen uniformly from
![]() $\mathbb{F}_p$
. By [
Reference Fulman and Goldstein12
, theorem 4·1], for
$\mathbb{F}_p$
. By [
Reference Fulman and Goldstein12
, theorem 4·1], for
![]() $\tau \in [n/20, n/2]$
and for any
$\tau \in [n/20, n/2]$
and for any
![]() $0 \leq k \leq n-\tau$
,
$0 \leq k \leq n-\tau$
,
which completes the proof.
Finally, we prove Lemma 3·2:
Proof of Lemma 3·2. Note that
![]() $\operatorname{rank} A_{t+1}-\operatorname{rank} A_t\in\{0,1,2\}$
since rank is monotone and sub-additive and the rank of the “reverse-L” is at most 2. Since the ambient dimension increases by 1 at each step, it follows that the corank increases by one of the three values
$\operatorname{rank} A_{t+1}-\operatorname{rank} A_t\in\{0,1,2\}$
since rank is monotone and sub-additive and the rank of the “reverse-L” is at most 2. Since the ambient dimension increases by 1 at each step, it follows that the corank increases by one of the three values
![]() $\{0,\pm1\}$
, so that it suffices to prove the first and third equalities. Write
$\{0,\pm1\}$
, so that it suffices to prove the first and third equalities. Write
where
![]() $\xi_t$
is an i.i.d. Rademacher vector and
$\xi_t$
is an i.i.d. Rademacher vector and
![]() $z+\lambda$
is an independent Rademacher. Let
$z+\lambda$
is an independent Rademacher. Let
![]() $\xi$
be the vector
$\xi$
be the vector
![]() $[\xi_t^T z]^T$
.
$[\xi_t^T z]^T$
.
Step 1. Corank decrease via linear forms. The first equality is only nontrivial when
![]() $k\ge 1$
, and in this case we need the rank to increase by 2. Basic linear algebra (cf. [
Reference Costello, Tao and Vu7
, lemma 2·4]) shows that this is equivalent to requiring
$k\ge 1$
, and in this case we need the rank to increase by 2. Basic linear algebra (cf. [
Reference Costello, Tao and Vu7
, lemma 2·4]) shows that this is equivalent to requiring
![]() $\xi_t$
to lie outside the span of the column space of
$\xi_t$
to lie outside the span of the column space of
![]() $A_t$
. Equivalently,
$A_t$
. Equivalently,
![]() $\xi_t$
should not be orthogonal to all kernel vectors of
$\xi_t$
should not be orthogonal to all kernel vectors of
![]() $A_t$
(which form a dimension k subspace of
$A_t$
(which form a dimension k subspace of
![]() $\mathbb{F}_p^t$
). Let
$\mathbb{F}_p^t$
). Let
![]() $\boldsymbol{v}_1,\ldots,\boldsymbol{v}_k$
form a basis of the kernel. We have
$\boldsymbol{v}_1,\ldots,\boldsymbol{v}_k$
form a basis of the kernel. We have
 \begin{align*}\left|\mathbb{P}_\xi[\boldsymbol{v}_j\cdot\xi_t = 0\text{ for all }j\in[k]]-p^{-k}\right| &= \bigg|\frac{1}{p^k}\sum_{\boldsymbol{a}\in\mathbb{F}_p^k\setminus\{\mathbf{0}\}}\mathbb{E}_\xi\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot(a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k))\bigg)\bigg|\\[6pt] &\le\max_{\boldsymbol{a}\in\mathbb{F}_p^k\setminus\{\boldsymbol{0}\}}\bigg|\mathbb{E}_\xi\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot(a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k))\bigg)\bigg|.\end{align*}
\begin{align*}\left|\mathbb{P}_\xi[\boldsymbol{v}_j\cdot\xi_t = 0\text{ for all }j\in[k]]-p^{-k}\right| &= \bigg|\frac{1}{p^k}\sum_{\boldsymbol{a}\in\mathbb{F}_p^k\setminus\{\mathbf{0}\}}\mathbb{E}_\xi\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot(a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k))\bigg)\bigg|\\[6pt] &\le\max_{\boldsymbol{a}\in\mathbb{F}_p^k\setminus\{\boldsymbol{0}\}}\bigg|\mathbb{E}_\xi\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot(a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k))\bigg)\bigg|.\end{align*}
Let
![]() $\boldsymbol{a} = (a_1,\dots, a_k) \in \mathbb{F}_p^{k} \setminus \{\boldsymbol{0}\}$
denote the element attaining the maximum. Since
$\boldsymbol{a} = (a_1,\dots, a_k) \in \mathbb{F}_p^{k} \setminus \{\boldsymbol{0}\}$
denote the element attaining the maximum. Since
![]() $\boldsymbol{v}_1,\dots, \boldsymbol{v}_k$
are linearly independent vectors in the kernel of
$\boldsymbol{v}_1,\dots, \boldsymbol{v}_k$
are linearly independent vectors in the kernel of
![]() $A_t$
,
$A_t$
,
![]() $\boldsymbol{v} = a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k$
is a nonzero kernel vector of
$\boldsymbol{v} = a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k$
is a nonzero kernel vector of
![]() $A_t$
. Since we have conditioned on
$A_t$
. Since we have conditioned on
![]() $\mathcal{E}_{S,t}\wedge \mathcal{E}_{U, t}$
,
$\mathcal{E}_{S,t}\wedge \mathcal{E}_{U, t}$
,
![]() $\boldsymbol{v}$
has at least
$\boldsymbol{v}$
has at least
![]() $t/(16\log p)$
nonzero entries and satisfies property (
$t/(16\log p)$
nonzero entries and satisfies property (
![]() $\dagger$
).
$\dagger$
).
From
![]() $\mathcal{E}_{U,t}$
we see that
$\mathcal{E}_{U,t}$
we see that
![]() $\boldsymbol{v}$
can be partitioned into at least
$\boldsymbol{v}$
can be partitioned into at least
![]() $t/(2m)$
disjoint sets
$t/(2m)$
disjoint sets
![]() $S_1,\dots, S_{t/(2m)}$
of size m with
$S_1,\dots, S_{t/(2m)}$
of size m with
![]() $\operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{v}|_{S_i})\le C_{2.5}p^{-2}$
for all
$\operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{v}|_{S_i})\le C_{2.5}p^{-2}$
for all
![]() $i \in [t/(2m)]$
. Hence,
$i \in [t/(2m)]$
. Hence,
 \begin{align*}\mathbb{E}_{\xi}\exp\left(\frac{2\pi i}{p}\xi_t\cdot \boldsymbol{v}\right) &\leq \prod_{\ell=1}^{t/(2m)}\left|\mathbb{E}_{\xi|_{S_\ell}}\exp\left(\frac{2\pi i}{p} \xi|_{S_\ell}\cdot \boldsymbol{v}|_{S_\ell}\right)\right|\\ &= \prod_{\ell=1}^{t/(2m)}\left|\sum_{j \in \mathbb{F}_p}\exp\left(\frac{2\pi i}{p}j\right)\cdot \left(\frac{1}{p} + \bigg(\mathbb{P}_{\xi}\bigg[\sum_{i\in S_{\ell}}v_i\xi_i \equiv j\bmod p\bigg]-\frac{1}{p}\bigg) \right)\right|\\ &\leq \prod_{\ell=1}^{t/(2m)}\left|\sum_{j \in \mathbb{F}_p}\operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{v}|_{S_\ell})\right|\\ &\leq (C_{2.5}p^{-1})^{t/(2m)} = \exp(\!-\Omega(t)),\end{align*}
\begin{align*}\mathbb{E}_{\xi}\exp\left(\frac{2\pi i}{p}\xi_t\cdot \boldsymbol{v}\right) &\leq \prod_{\ell=1}^{t/(2m)}\left|\mathbb{E}_{\xi|_{S_\ell}}\exp\left(\frac{2\pi i}{p} \xi|_{S_\ell}\cdot \boldsymbol{v}|_{S_\ell}\right)\right|\\ &= \prod_{\ell=1}^{t/(2m)}\left|\sum_{j \in \mathbb{F}_p}\exp\left(\frac{2\pi i}{p}j\right)\cdot \left(\frac{1}{p} + \bigg(\mathbb{P}_{\xi}\bigg[\sum_{i\in S_{\ell}}v_i\xi_i \equiv j\bmod p\bigg]-\frac{1}{p}\bigg) \right)\right|\\ &\leq \prod_{\ell=1}^{t/(2m)}\left|\sum_{j \in \mathbb{F}_p}\operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{v}|_{S_\ell})\right|\\ &\leq (C_{2.5}p^{-1})^{t/(2m)} = \exp(\!-\Omega(t)),\end{align*}
if
![]() $p > C_{2.5}$
.
$p > C_{2.5}$
.
From
![]() $\mathcal{E}_{S,t}$
we see that
$\mathcal{E}_{S,t}$
we see that
![]() $\boldsymbol{v}$
has support size at least
$\boldsymbol{v}$
has support size at least
![]() $t/(16\log p)$
, so that
$t/(16\log p)$
, so that
 \begin{align*}\mathbb{E}_{\xi}\exp\left(\frac{2\pi i}{p}\xi_t\cdot \boldsymbol{v}\right) &\leq \prod_{j \in \operatorname{supp}\!(\boldsymbol{v})}\left|\mathbb{E}_{\xi_j}\exp\left(\frac{2\pi i}{p}\xi_j v_j\right)\right|\\ &\leq (1-\Omega(1/p^2))^{t/(16\log{p})}\\ &= \exp(\!-\Omega(t/(p^2\log p))) = \exp(\!-\Omega(t)),\end{align*}
\begin{align*}\mathbb{E}_{\xi}\exp\left(\frac{2\pi i}{p}\xi_t\cdot \boldsymbol{v}\right) &\leq \prod_{j \in \operatorname{supp}\!(\boldsymbol{v})}\left|\mathbb{E}_{\xi_j}\exp\left(\frac{2\pi i}{p}\xi_j v_j\right)\right|\\ &\leq (1-\Omega(1/p^2))^{t/(16\log{p})}\\ &= \exp(\!-\Omega(t/(p^2\log p))) = \exp(\!-\Omega(t)),\end{align*}
if
![]() $p\le C_{2.5}$
. Therefore regardless of what
$p\le C_{2.5}$
. Therefore regardless of what
![]() $p > 2$
is, we have
$p > 2$
is, we have
as desired to establish the first equality.
Step 2. Corank increase via quadratic forms. Now we turn to the third equality. First note that it suffices to prove the claim when
![]() $k\le t/(64\log p)$
since if
$k\le t/(64\log p)$
since if
![]() $k > t/(64\log p)$
, the first equality already implies that the second and third probabilities are of size
$k > t/(64\log p)$
, the first equality already implies that the second and third probabilities are of size
![]() $p^{-k} + O(\!\exp(\!-\Omega(t))) = O(\!\exp(\!-\Omega(t)))$
.
$p^{-k} + O(\!\exp(\!-\Omega(t))) = O(\!\exp(\!-\Omega(t)))$
.
By Lemma 3·1,
![]() $A_t$
has a principal minor of rank
$A_t$
has a principal minor of rank
![]() $(t-k)$
. Therefore, without loss of generality, we may suppose that the top left
$(t-k)$
. Therefore, without loss of generality, we may suppose that the top left
![]() $(t-k)\times(t-k)$
block, call it B, has full rank. Let
$(t-k)\times(t-k)$
block, call it B, has full rank. Let
![]() $\phi$
be the restriction of
$\phi$
be the restriction of
![]() $\xi$
to these coordinates. In order for the corank of
$\xi$
to these coordinates. In order for the corank of
![]() $A_{t+1}$
to be larger than the corank of
$A_{t+1}$
to be larger than the corank of
![]() $A_{t}$
, it must be the case that
$A_{t}$
, it must be the case that
![]() $\operatorname{rank}(A_{t+1}) = \operatorname{rank}(A_{t})$
. This precisely corresponds to the event
$\operatorname{rank}(A_{t+1}) = \operatorname{rank}(A_{t})$
. This precisely corresponds to the event
Indeed, if
![]() $\xi_t$
is not in the column space then the rank of
$\xi_t$
is not in the column space then the rank of
![]() $A_{t+1}$
must increase and if
$A_{t+1}$
must increase and if
![]() $\phi^TB^{-1}\phi\neq -z$
, then B along with the new elements in the “reverse-L” will have rank
$\phi^TB^{-1}\phi\neq -z$
, then B along with the new elements in the “reverse-L” will have rank
![]() $(t-k+1)$
. On the other hand, if the above event holds, then it is easy to see that
$(t-k+1)$
. On the other hand, if the above event holds, then it is easy to see that
![]() $\operatorname{rank}(A_{t+1}) = \operatorname{rank}(A_t)$
.
$\operatorname{rank}(A_{t+1}) = \operatorname{rank}(A_t)$
.
As in the first case, let
![]() $\boldsymbol{v}_1,\dots, \boldsymbol{v}_k$
form a basis of the kernel of
$\boldsymbol{v}_1,\dots, \boldsymbol{v}_k$
form a basis of the kernel of
![]() $A_{t}$
. Then,
$A_{t}$
. Then,
 \begin{align*}\bigg|\mathbb{P}_\xi[\boldsymbol{v}_j\cdot\xi_t &= 0\text{ for all }j\in[k]\wedge\phi^TB^{-1}\phi = z] - p^{-k-1}\bigg|\\&\le\sup_{\boldsymbol{a}\in\mathbb{F}_p^{k+1}\setminus\{\mathbf{0}\}}\bigg|\mathbb{E}_\xi\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot(a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k) + a_{k+1}(\phi^TB^{-1}\phi-z))\bigg)\bigg|.\end{align*}
\begin{align*}\bigg|\mathbb{P}_\xi[\boldsymbol{v}_j\cdot\xi_t &= 0\text{ for all }j\in[k]\wedge\phi^TB^{-1}\phi = z] - p^{-k-1}\bigg|\\&\le\sup_{\boldsymbol{a}\in\mathbb{F}_p^{k+1}\setminus\{\mathbf{0}\}}\bigg|\mathbb{E}_\xi\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot(a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k) + a_{k+1}(\phi^TB^{-1}\phi-z))\bigg)\bigg|.\end{align*}
Note here that
![]() $\xi_t,\phi,z$
all depend on
$\xi_t,\phi,z$
all depend on
![]() $\xi$
. Let
$\xi$
. Let
![]() $\boldsymbol{a} = (a_1,\dots, a_{k+1}) \in \mathbb{F}_p^{k+1}\setminus \{\boldsymbol{0}\}$
denote the element attaining the maximum. If
$\boldsymbol{a} = (a_1,\dots, a_{k+1}) \in \mathbb{F}_p^{k+1}\setminus \{\boldsymbol{0}\}$
denote the element attaining the maximum. If
![]() $a_{k+1} = 0$
, we have a bound of
$a_{k+1} = 0$
, we have a bound of
![]() $\exp(\!-\Omega(t))$
exactly as in the first case. It therefore suffices to consider
$\exp(\!-\Omega(t))$
exactly as in the first case. It therefore suffices to consider
![]() $a_{k+1}\neq 0$
. Let
$a_{k+1}\neq 0$
. Let
![]() $\boldsymbol{v} = a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k$
.
$\boldsymbol{v} = a_1\boldsymbol{v}_1+\cdots+a_k\boldsymbol{v}_k$
.
To handle the quadratic term
![]() $\phi^T B^{-1} \phi$
, we will use a decoupling trick, which in this context essentially goes back to [
Reference Costello, Tao and Vu7
]. Let
$\phi^T B^{-1} \phi$
, we will use a decoupling trick, which in this context essentially goes back to [
Reference Costello, Tao and Vu7
]. Let
![]() $I\sqcup J = \{1,\ldots,t\}$
be the partition with
$I\sqcup J = \{1,\ldots,t\}$
be the partition with
![]() $J = [t/(64\log p)]$
, and let
$J = [t/(64\log p)]$
, and let
![]() $\xi_I,\xi_J$
be the obvious restrictions. Let
$\xi_I,\xi_J$
be the obvious restrictions. Let
![]() $\xi_J^{\prime}$
be an independent resample of
$\xi_J^{\prime}$
be an independent resample of
![]() $\xi_J$
. Let
$\xi_J$
. Let
![]() $\xi = \xi_I+\xi_J$
and
$\xi = \xi_I+\xi_J$
and
![]() $\xi' = \xi_I+\xi_J^{\prime}$
. Let
$\xi' = \xi_I+\xi_J^{\prime}$
. Let
![]() $\phi' = \xi'\mid_{[t-k]}$
. We have that
$\phi' = \xi'\mid_{[t-k]}$
. We have that
 \begin{align*}\bigg|\mathbb{E}_\xi&\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot \boldsymbol{v} + a_{k+1}(\phi^TB^{-1}\phi - z))\bigg)\bigg|^2\\&= \mathbb{E}_{\xi_I,\xi_J,\xi_J^{\prime}}\exp\bigg(\frac{2\pi i}{p}((\xi_J-\xi_J^{\prime})\cdot\boldsymbol{v} + a_{k+1}(\phi^TB^{-1}\phi - (\phi')^TB^{-1}\phi'))\bigg)\\&\leq \mathbb{E}_{\xi_J,\xi_J^{\prime}}\left|\mathbb{E}_{\xi_I}\left[\exp\left(\frac{2\pi i}{p} a_{k+1}(\phi - \phi')^T B^{-1}(\phi + \phi') \right)\bigg | \xi_J, \xi^{\prime}_J\right]\right| \\&\le\mathbb{E}_{\xi_J,\xi_J^{\prime}}\bigg|\mathbb{E}_{\xi_I}\bigg[\exp\bigg(\frac{2\pi i}{p}(2a_{k+1}(\xi_J-\xi_J^{\prime})^TB^{-1}\phi'')\bigg)\bigg|\xi_J,\xi_J^{\prime}\bigg]\bigg|,\end{align*}
\begin{align*}\bigg|\mathbb{E}_\xi&\exp\bigg(\frac{2\pi i}{p}(\xi_t\cdot \boldsymbol{v} + a_{k+1}(\phi^TB^{-1}\phi - z))\bigg)\bigg|^2\\&= \mathbb{E}_{\xi_I,\xi_J,\xi_J^{\prime}}\exp\bigg(\frac{2\pi i}{p}((\xi_J-\xi_J^{\prime})\cdot\boldsymbol{v} + a_{k+1}(\phi^TB^{-1}\phi - (\phi')^TB^{-1}\phi'))\bigg)\\&\leq \mathbb{E}_{\xi_J,\xi_J^{\prime}}\left|\mathbb{E}_{\xi_I}\left[\exp\left(\frac{2\pi i}{p} a_{k+1}(\phi - \phi')^T B^{-1}(\phi + \phi') \right)\bigg | \xi_J, \xi^{\prime}_J\right]\right| \\&\le\mathbb{E}_{\xi_J,\xi_J^{\prime}}\bigg|\mathbb{E}_{\xi_I}\bigg[\exp\bigg(\frac{2\pi i}{p}(2a_{k+1}(\xi_J-\xi_J^{\prime})^TB^{-1}\phi'')\bigg)\bigg|\xi_J,\xi_J^{\prime}\bigg]\bigg|,\end{align*}
where we have abused notation by using
![]() $\xi_J - \xi^{\prime}_J$
to denote the extension of this vector to
$\xi_J - \xi^{\prime}_J$
to denote the extension of this vector to
![]() $[t-k]$
with the coordinates in
$[t-k]$
with the coordinates in
![]() $[t-k]\setminus J$
equal to 0 and where
$[t-k]\setminus J$
equal to 0 and where
![]() $\phi''$
denotes the
$\phi''$
denotes the
![]() $(t-k)$
-dimensional vector which coincides with
$(t-k)$
-dimensional vector which coincides with
![]() $\xi$
(and hence
$\xi$
(and hence
![]() $\xi'$
) on
$\xi'$
) on
![]() $I \cap [t-k]$
and has remaining coordinates 0.
$I \cap [t-k]$
and has remaining coordinates 0.
We now consider two cases. Note that
![]() $\mathbb{P}[\xi_J = \xi_J^{\prime}] = 2^{-|J|}$
, which is of size exp
$\mathbb{P}[\xi_J = \xi_J^{\prime}] = 2^{-|J|}$
, which is of size exp
![]() $(\!-\Omega(t/\log p))$
. Otherwise,
$(\!-\Omega(t/\log p))$
. Otherwise,
![]() $\boldsymbol{w} = B^{-1}(\xi_J-\xi^{\prime}_{J})$
is a linear combination of at most
$\boldsymbol{w} = B^{-1}(\xi_J-\xi^{\prime}_{J})$
is a linear combination of at most
![]() $t/(64\log p)$
different columns of
$t/(64\log p)$
different columns of
![]() $B^{-1}$
and hence is orthogonal to at least
$B^{-1}$
and hence is orthogonal to at least
![]() $(t-k) -t/(64\log p) \geq t/(32\log{p})$
different rows of B. Hence, if we extend
$(t-k) -t/(64\log p) \geq t/(32\log{p})$
different rows of B. Hence, if we extend
![]() $\boldsymbol{w}$
to a t-dimensional vector by padding it with 0s, then the resulting vector is a nonzero vector which is orthogonal to at least
$\boldsymbol{w}$
to a t-dimensional vector by padding it with 0s, then the resulting vector is a nonzero vector which is orthogonal to at least
![]() $t-t/(32\log{p})$
rows of
$t-t/(32\log{p})$
rows of
![]() $A_t$
. Since
$A_t$
. Since
![]() $A_{t}$
is assumed to satisfy
$A_{t}$
is assumed to satisfy
![]() $\mathcal{E}_{U,t}$
, it follows that this vector has at least
$\mathcal{E}_{U,t}$
, it follows that this vector has at least
![]() $t/(2m)$
disjoint sets
$t/(2m)$
disjoint sets
![]() $S_1,\dots, S_{t/(2m)}$
of size
$S_1,\dots, S_{t/(2m)}$
of size
![]() $m = C_{2.5}\log p$
such that
$m = C_{2.5}\log p$
such that
![]() $\operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{v}|_{S_i})\le C_{2.5}p^{-2}$
for all
$\operatorname{disc}_{\mathbb{F}_p}\!(\boldsymbol{v}|_{S_i})\le C_{2.5}p^{-2}$
for all
![]() $i \in [2m]$
. Furthermore
$i \in [2m]$
. Furthermore
![]() $\mathcal{E}_{U,t}$
guarantees that we can take these sets disjoint from the set
$\mathcal{E}_{U,t}$
guarantees that we can take these sets disjoint from the set
![]() $J\cup\{t-k+1,\ldots,t\}$
which has size at most
$J\cup\{t-k+1,\ldots,t\}$
which has size at most
![]() $t/(32\log{p})$
. In other words, the sets
$t/(32\log{p})$
. In other words, the sets
![]() $S_1,\dots, S_{t/(2m)}$
are contained in
$S_1,\dots, S_{t/(2m)}$
are contained in
![]() $I \cap [t-k]$
, which is the support of the random entries of
$I \cap [t-k]$
, which is the support of the random entries of
![]() $\phi''$
. Thus, similar to Step 1, we deduce for realizations of
$\phi''$
. Thus, similar to Step 1, we deduce for realizations of
![]() $\xi_J,\xi_J^{\prime}$
such that
$\xi_J,\xi_J^{\prime}$
such that
![]() $\xi_{J} - \xi^{\prime}_{J} \neq 0$
,
$\xi_{J} - \xi^{\prime}_{J} \neq 0$
,
for
![]() $p > C_{2.5}$
. For
$p > C_{2.5}$
. For
![]() $p\le C_{2.5}$
, we use
$p\le C_{2.5}$
, we use
![]() $\mathcal{E}_{S,t}$
to deduce that
$\mathcal{E}_{S,t}$
to deduce that
![]() $\boldsymbol{w}$
has support size at least
$\boldsymbol{w}$
has support size at least
![]() $t/(16\log p)$
. Therefore,
$t/(16\log p)$
. Therefore,
![]() $\boldsymbol{w}$
has at least
$\boldsymbol{w}$
has at least
![]() $t/(32\log p)$
on the support of the random entries of
$t/(32\log p)$
on the support of the random entries of
![]() $\phi''$
, so that the result again follows as in Step 1.
$\phi''$
, so that the result again follows as in Step 1.
Acknowledgements
We are grateful to the anonymous referee for their careful reading of the manuscript and for their suggestions. We thank Van Vu for clarifying the history of the conjecture about the irreducibility of the characteristic polynomial.
Appendix A. Proof of Theorem 1·1
In this section, we show how the local singularity statement Theorem 1·2 implies the global irreducibility statement Theorem 1·1. We use an approach pioneered by Breuillard and Varjú [ Reference Breuillard and Varjú3 ] for random polynomials and used subsequently by Eberhard [ Reference Eberhard8 ] for characteristic polynomials of i.i.d. matrices. The proof is nearly identical to that given in [ Reference Eberhard8 , section 3] modulo the input of Theorem 1·2.
We first define some notation. Let
![]() $\Omega\subseteq\mathbb{C}$
be the set of roots of
$\Omega\subseteq\mathbb{C}$
be the set of roots of
![]() $\varphi$
and G be its Galois group. Let
$\varphi$
and G be its Galois group. Let
![]() $R_\varphi(p)$
be the number of roots of
$R_\varphi(p)$
be the number of roots of
![]() $\varphi$
in
$\varphi$
in
![]() $\mathbb{F}_p$
, without multiplicity.
$\mathbb{F}_p$
, without multiplicity.
Now let
be a weighting function.
Proposition A·1 ([
Reference Eberhard8
, proposition 3·5]). Let
![]() $\varphi$
be the characteristic polynomial of a matrix M with integer entries bounded in magnitude by H. If the Riemann hypothesis holds for
$\varphi$
be the characteristic polynomial of a matrix M with integer entries bounded in magnitude by H. If the Riemann hypothesis holds for
![]() $\mathbb{Q}(\omega)$
for all roots
$\mathbb{Q}(\omega)$
for all roots
![]() $\omega$
of
$\omega$
of
![]() $\varphi$
, then
$\varphi$
, then
Finally, we state the following bound on the probability for a symmetric Rademacher matrix to have simple spectrum.
Proposition A·2. The
![]() $n\times n$
random symmetric Rademacher matrix
$n\times n$
random symmetric Rademacher matrix
![]() $M_n$
has simple spectrum with probability
$M_n$
has simple spectrum with probability
![]() $1-\exp(\!-\Omega(n^{1/2}(\log n)^{1/4}))$
.
$1-\exp(\!-\Omega(n^{1/2}(\log n)^{1/4}))$
.
Remark. A bound of the form
![]() $1 - \exp(\!-\Omega(n^{c})))$
for some small constant
$1 - \exp(\!-\Omega(n^{c})))$
for some small constant
![]() $c > 0$
is the content of [
Reference Nguyen, Tao and Vu19
, corollary 2·3]. The improved bound stated here follows by replacing the application of the results of [
Reference Vershynin24
] in [
Reference Nguyen, Tao and Vu19
] by the substantially sharper arithmetic structure estimates [
Reference Jain, Sah and Sawhney14
, theorem 4·8; lemma 4·5] appearing in work of the last three authors [
Reference Jain, Sah and Sawhney14
]. We omit the standard details.
$c > 0$
is the content of [
Reference Nguyen, Tao and Vu19
, corollary 2·3]. The improved bound stated here follows by replacing the application of the results of [
Reference Vershynin24
] in [
Reference Nguyen, Tao and Vu19
] by the substantially sharper arithmetic structure estimates [
Reference Jain, Sah and Sawhney14
, theorem 4·8; lemma 4·5] appearing in work of the last three authors [
Reference Jain, Sah and Sawhney14
]. We omit the standard details.
We are ready to prove the result.
Proof of Theorem 1·1 given Theorem 1·2. Given a prime
![]() $p > 2$
and
$p > 2$
and
![]() $\lambda\in\mathbb{F}_p$
, let
$\lambda\in\mathbb{F}_p$
, let
![]() $\mathcal{E}_{p,\lambda}$
be the event that the characteristic polynomial
$\mathcal{E}_{p,\lambda}$
be the event that the characteristic polynomial
![]() $\varphi$
of our random symmetric matrix
$\varphi$
of our random symmetric matrix
![]() $M_n$
has
$M_n$
has
![]() $\lambda$
as a root over
$\lambda$
as a root over
![]() $\mathbb{F}_p$
. By Theorem 1·2 applied to
$\mathbb{F}_p$
. By Theorem 1·2 applied to
![]() $M_n-\lambda I_n$
, we see that if
$M_n-\lambda I_n$
, we see that if
![]() $2 < p\le\exp(c_{1.2}n^{1/4})$
, then
$2 < p\le\exp(c_{1.2}n^{1/4})$
, then
Summing over
![]() $\lambda$
yields
$\lambda$
yields
Thus for
![]() $2\le X\le c_{1.2}n^{1/4}$
we have
$2\le X\le c_{1.2}n^{1/4}$
we have
 \begin{align*}\mathbb{E}\sum_pR_\varphi(p)w_X(\log p) &= \sum_p(1 + O(1/p))w_X(\log p)\\&= (1 + O(\!\exp(\!-X/2)))\sum_pw_X(\log p)\\&= 1 + O(\!\exp(\!-X/2)) + O(X^2\exp(\!-X/2)).\end{align*}
\begin{align*}\mathbb{E}\sum_pR_\varphi(p)w_X(\log p) &= \sum_p(1 + O(1/p))w_X(\log p)\\&= (1 + O(\!\exp(\!-X/2)))\sum_pw_X(\log p)\\&= 1 + O(\!\exp(\!-X/2)) + O(X^2\exp(\!-X/2)).\end{align*}
The third line is by the Riemann hypothesis for
![]() $\mathbb{Q}$
. Applying Proposition A·1 under ERH we obtain
$\mathbb{Q}$
. Applying Proposition A·1 under ERH we obtain
hence
Choosing
![]() $X = c_{1.2}n^{1/4}$
at the top of its range, we deduce
$X = c_{1.2}n^{1/4}$
at the top of its range, we deduce
Thus
Furthermore,
![]() $|\Omega/G| = 1$
means that
$|\Omega/G| = 1$
means that
![]() $\varphi$
is a perfect power of an irreducible polynomial.
$\varphi$
is a perfect power of an irreducible polynomial.
Now to rule out the case of perfect powers and complete the proof, it suffices to show that the random symmetric matrix
![]() $M_n$
has simple spectrum with very high probability, say at least
$M_n$
has simple spectrum with very high probability, say at least
![]() $1-\exp(\!-\Omega(\sqrt{n}))$
. This is the content of Proposition A·2.
$1-\exp(\!-\Omega(\sqrt{n}))$
. This is the content of Proposition A·2.
B. Proof of Proposition 2·4
We require a version of Halasz’s inequality as well as a ‘counting inverse Littlewood–Offord theorem’ tailored to it. This was developed in work of the first two authors along with Luh and Samotij [ Reference Ferber, Jain, Luh and Samotij11 ].
Definition B·1. Let
![]() $\boldsymbol{a}\in\mathbb{F}_p^n$
and
$\boldsymbol{a}\in\mathbb{F}_p^n$
and
![]() $k\in\mathbb{N}$
. We define
$k\in\mathbb{N}$
. We define
![]() $R_k^{\ast}(\boldsymbol{a})$
to be the number of solutions to
$R_k^{\ast}(\boldsymbol{a})$
to be the number of solutions to
with
![]() $|\{i_1,\ldots,i_{2k}\}|>1.01k$
.
$|\{i_1,\ldots,i_{2k}\}|>1.01k$
.
Theorem B·2 ([
Reference Jain13
, theorem 3·8], c.f. [
Reference Ferber, Jain, Luh and Samotij11
, theorem 1·4]). Given an odd prime p, integer n, and vector
![]() $\boldsymbol{a}=(a_1,\ldots, a_n) \in\mathbb{F}_p^{n}\setminus\{\boldsymbol{0}\}$
, suppose that an integer
$\boldsymbol{a}=(a_1,\ldots, a_n) \in\mathbb{F}_p^{n}\setminus\{\boldsymbol{0}\}$
, suppose that an integer
![]() $0\le k \le n/2$
and positive real L satisfy
$0\le k \le n/2$
and positive real L satisfy
![]() $30L \le |\operatorname{supp}\!(\boldsymbol{a})|$
and
$30L \le |\operatorname{supp}\!(\boldsymbol{a})|$
and
![]() $80kL \le n$
. Then
$80kL \le n$
. Then
Theorem B·3 ([
Reference Ferber and Jain10
, corollary 3·11]). Let p be a prime and let
![]() $k, s_1,s_2,d\in [n], t\in [1,p]$
be such that
$k, s_1,s_2,d\in [n], t\in [1,p]$
be such that
![]() $s_1 \le s_2\le d$
. Let
$s_1 \le s_2\le d$
. Let
 \begin{align*}& \textrm{Bad}^{d}_{k,s_1,s_2,\ge t}(n) = \\ & \Big\{\boldsymbol{a} \in \mathbb{F}_{p}^{n}\colon |\operatorname{supp}\!(\boldsymbol{a})|=d \text{ and } \forall \boldsymbol{b}\subseteq \boldsymbol{a}|_{\operatorname{supp}\!(\boldsymbol{a})} \text{ s.t. } s_2\ge|\boldsymbol{b}|\ge s_1 \;:\; R_k^\ast(\boldsymbol{b})\ge t\cdot \frac{2^{2k}\cdot |\boldsymbol{b}|^{2k}}{p}\Big\}.\end{align*}
\begin{align*}& \textrm{Bad}^{d}_{k,s_1,s_2,\ge t}(n) = \\ & \Big\{\boldsymbol{a} \in \mathbb{F}_{p}^{n}\colon |\operatorname{supp}\!(\boldsymbol{a})|=d \text{ and } \forall \boldsymbol{b}\subseteq \boldsymbol{a}|_{\operatorname{supp}\!(\boldsymbol{a})} \text{ s.t. } s_2\ge|\boldsymbol{b}|\ge s_1 \;:\; R_k^\ast(\boldsymbol{b})\ge t\cdot \frac{2^{2k}\cdot |\boldsymbol{b}|^{2k}}{p}\Big\}.\end{align*}
Then,
We now are in position to prove Proposition 2·4. The proof given is essentially identical to that in [ Reference Ferber and Jain10 ]. However, we need to be more careful regarding the level of unstructuredness obtained in the argument.
Proof of Proposition 2·4. Let
![]() $r = n/\log p$
. Let
$r = n/\log p$
. Let
![]() $k = n^{1/4}$
,
$k = n^{1/4}$
,
![]() $s_1 = \sqrt{n\log n}$
,
$s_1 = \sqrt{n\log n}$
,
![]() $s_2 = n^{3/4}$
, and choose some
$s_2 = n^{3/4}$
, and choose some
![]() $n/(16\log p)\le d\le n$
(so that
$n/(16\log p)\le d\le n$
(so that
![]() $s_2\le d$
in particular). First use Lemma 2·2 to rule out d-sparse vectors
$s_2\le d$
in particular). First use Lemma 2·2 to rule out d-sparse vectors
![]() $\boldsymbol{v}$
. Next, let
$\boldsymbol{v}$
. Next, let
![]() $L = n^{1/4}$
. Consider some
$L = n^{1/4}$
. Consider some
![]() $\sqrt{L}\le t\le p$
, if it exists.
$\sqrt{L}\le t\le p$
, if it exists.
Consider a fixed
![]() $\boldsymbol{v}\in\textrm{Bad}_{k,s_1,s_2,\ge t}^d\setminus\textrm{Bad}_{k,s_1,s_2,\ge 2t}^d$
and a fixed choice of
$\boldsymbol{v}\in\textrm{Bad}_{k,s_1,s_2,\ge t}^d\setminus\textrm{Bad}_{k,s_1,s_2,\ge 2t}^d$
and a fixed choice of
![]() $n-r$
rows of
$n-r$
rows of
![]() $M_n-\lambda I_n$
. We wish to bound the probability that
$M_n-\lambda I_n$
. We wish to bound the probability that
![]() $\boldsymbol{v}$
is orthogonal to all those rows. By definition, there is a set
$\boldsymbol{v}$
is orthogonal to all those rows. By definition, there is a set
![]() $S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
of size in
$S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
of size in
![]() $[s_1,s_2]$
such that
$[s_1,s_2]$
such that
Since
![]() $\boldsymbol{v}$
is orthogonal to all of the given
$\boldsymbol{v}$
is orthogonal to all of the given
![]() $n-r$
rows, we expose them one-by-one (with any rows in S coming last). The first at least
$n-r$
rows, we expose them one-by-one (with any rows in S coming last). The first at least
![]() $n-r-s_2$
rows are such that, conditioned on the prior revelations, the random dot product with
$n-r-s_2$
rows are such that, conditioned on the prior revelations, the random dot product with
![]() $\boldsymbol{v}$
is zero with probability at most
$\boldsymbol{v}$
is zero with probability at most
![]() $\rho_{\mathbb{F}_p}\!(\boldsymbol{v}|_S)$
. Furthermore, by Theorem B·2 and the given conditions, which guarantee
$\rho_{\mathbb{F}_p}\!(\boldsymbol{v}|_S)$
. Furthermore, by Theorem B·2 and the given conditions, which guarantee
![]() $30L\le s_1\le|\operatorname{supp}(\boldsymbol{v}|_S)|$
and
$30L\le s_1\le|\operatorname{supp}(\boldsymbol{v}|_S)|$
and
![]() $80kL\le s_1\le|S|$
, we have
$80kL\le s_1\le|S|$
, we have
 \begin{align*}\rho_{\mathbb{F}_p}(\boldsymbol{v}|_S)&\le\frac{1}{p}+C_{3.2}\frac{R_k^\ast(\boldsymbol{v}|_S) + (40k^{0.99}|S|^{1.01})^k}{2^{2k} |S|^{2k} L^{1/2}} + e^{-L}\\&\le\frac{1}{p} + \frac{2C_{3.2}t}{p\sqrt{L}} + \frac{10^k C_{3.2}}{L^{1/2}}\bigg(\frac{k}{|S|}\bigg)^{0.99k} + e^{-L}\\&\le\frac{Ct}{p\sqrt{L}}\end{align*}
\begin{align*}\rho_{\mathbb{F}_p}(\boldsymbol{v}|_S)&\le\frac{1}{p}+C_{3.2}\frac{R_k^\ast(\boldsymbol{v}|_S) + (40k^{0.99}|S|^{1.01})^k}{2^{2k} |S|^{2k} L^{1/2}} + e^{-L}\\&\le\frac{1}{p} + \frac{2C_{3.2}t}{p\sqrt{L}} + \frac{10^k C_{3.2}}{L^{1/2}}\bigg(\frac{k}{|S|}\bigg)^{0.99k} + e^{-L}\\&\le\frac{Ct}{p\sqrt{L}}\end{align*}
for all sufficiently large n. Multiplying over all the rows, and taking a union bound over the possible choices of
![]() $\boldsymbol{v}$
(Theorem B·3) and collection of
$\boldsymbol{v}$
(Theorem B·3) and collection of
![]() $n-r$
rows, we have a bound of
$n-r$
rows, we have a bound of
 \begin{align*}\binom{n}{d}p^{d+s_2}(0.01t)^{-d+\frac{s_1}{s_2}d}&\cdot\binom{n}{r}\cdot\bigg(\frac{Ct}{p\sqrt{L}}\bigg)^{n-r-s_2}\\&\le (C')^np^dt^{-d+\frac{s_1}{s_2}d}\bigg(\frac{t}{p\sqrt{L}}\bigg)^n\\&\le\exp(C''n\sqrt{\log n})(t/p)^{n-d}L^{-n/2}\le\exp(\!-n(\log n)/9)\end{align*}
\begin{align*}\binom{n}{d}p^{d+s_2}(0.01t)^{-d+\frac{s_1}{s_2}d}&\cdot\binom{n}{r}\cdot\bigg(\frac{Ct}{p\sqrt{L}}\bigg)^{n-r-s_2}\\&\le (C')^np^dt^{-d+\frac{s_1}{s_2}d}\bigg(\frac{t}{p\sqrt{L}}\bigg)^n\\&\le\exp(C''n\sqrt{\log n})(t/p)^{n-d}L^{-n/2}\le\exp(\!-n(\log n)/9)\end{align*}
for sufficiently large n. Union bounding over all possible choices of d and a dyadic partition of t shows that there is an appropriately small chance of having such a vector orthogonal to
![]() $n-r$
rows for any
$n-r$
rows for any
![]() $t\ge\sqrt{L}$
.
$t\ge\sqrt{L}$
.
The remaining vectors
![]() $\boldsymbol{v} \in \mathbb{F}_p^n$
with
$\boldsymbol{v} \in \mathbb{F}_p^n$
with
![]() $|\operatorname{supp}\!(\boldsymbol{v})| \geq n/(16\log{p})$
all have some subset
$|\operatorname{supp}\!(\boldsymbol{v})| \geq n/(16\log{p})$
all have some subset
![]() $S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
such that
$S\subseteq\operatorname{supp}\!(\boldsymbol{v})$
such that
and applying Theorem B·2 once again completes the proof.