Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-07T21:57:15.185Z Has data issue: false hasContentIssue false
  • English
  • Français

An intuitionistic set-theoretical model of fully dependent CC$^{\boldsymbol\omega}$

Published online by Cambridge University Press:  17 April 2023

Masahiro Sato  and
Jacques Garrigue Open the ORCID record for Jacques Garrigue [Opens in a new window]
Masahiro Sato
Affiliation:
SIOS Technology, Inc., 2-12-3 Minami-Asabu, Minato-ku, Tokyo 106-0047, Japan
Jacques Garrigue*
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan
*
*Corresponding author. Email: garrigue@math.nagoya-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Werner’s set-theoretical model is one of the simplest models of CIC. It combines a functional view of predicative universes with a collapsed view of the impredicative sort “ 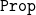${\tt Prop}$ ”. However, this model of 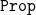${\tt Prop}$ is so coarse that the principle of excluded middle 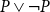$P \lor \neg P$ holds. Following our previous work, we interpret 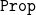${\tt Prop}$ into a topological space (a special case of Heyting algebra) to make the model more intuitionistic without sacrificing simplicity. We improve on that work by providing a full interpretation of dependent product types, using Alexandroff spaces. We also extend our approach to inductive types by adding support for 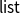${\mathsf{list}}$ s.

Keywords

type theorymodelintuitionistic logic
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 33 , Issue 1 , January 2023 , pp. 1 - 32
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aczel, P. (1998). On relating type theories and set theories. In: Proceedings of Types, Springer LNCS, vol. 1657, 1–18.Google Scholar
Aczel, P. and Rathjen, M. (2010). CST Book draft. https://www1.maths.leeds.ac.uk/~rathjen/book.pdf Google Scholar
Arenas, F. G. (1999). Alexandroff spaces. Acta Mathematica Universitatis Comenianae 68 (1) 17–25.Google Scholar
Barendregt, H. (1991). Introduction to generalized type systems. Journal of Functional Programming 1 (2) 125–154.CrossRefGoogle Scholar
Barendregt, H. (1992). Lambda calculus with types. In: Handbook of Logic in Computer Science, Chapter 2, vol. 2, Oxford University Press.Google Scholar
Barras, B. (2010). Sets in coq, coq in sets. Journal of Formalized Reasoning 3 (1) 29–48.Google Scholar
Coquand, T. and Huet, G. (1988). The calculus of constructions. Information and Computation 76 (2) 95–120.CrossRefGoogle Scholar
Dybjer, P. (2000). A general formulation of simultaneous inductive-recursive definitions in type theory. Journal of Symbolic Logic 65 (2) 525–549.CrossRefGoogle Scholar
Forster, Y. (2021). Church’s thesis and related axioms in Coq’s type theory. In: 29th EACSL Annual Conference on Computer Science Logic (CSL 2021), LIPIcs, vol. 183, 21:1–21:19.Google Scholar
Geuvers, H. (2001). Induction is not derivable in second order dependent type theory. In: Types for Proofs and Programs.Google Scholar
Girard, J.-Y. (1989). Proofs and Types, Cambridge University Press.Google Scholar
Jacobs, B. (2001). Categorical Logic and Type Theory , Studies in Logic and the Foundations of Mathematics, vol. 141, Elsevier.Google Scholar
Jiménez, B. C. R. (1999). Condensing lemmas for pure type systems with universes. In: Algebraic Methodology and Software Technology, Springer LNCS, vol. 1548, 422–437.CrossRefGoogle Scholar
Lee, G. and Werner, B. (2011). Proof-irrelevant model of CC with predicative induction and judgemental equality. Logical Methods in Computer Science 7 (4:5). https://doi.org/10.2168/LMCS-7(4:5)2011https://doi.org/10.2168/LMCS-7(4:5)2011 CrossRefGoogle Scholar
Luo, Z. (1991). A higher-order calculus and theory abstraction. Information and Computation 90 (1) 107–137.CrossRefGoogle Scholar
MacLane, S. and Moerdijk, I. (1992). Sheaves in Geometry and Logic: A First Introduction to Topos Theory, New York, Springer.Google Scholar
Miquel, A. and Werner, B. (2003). The not so simple proof-irrelevant model of CC. In: Types for Proof and Programs, Springer LNCS, vol. 2426, 240–258.CrossRefGoogle Scholar
Reynolds, J. (1984). Polymorphism is not set-theoretic. In: Semantics of Data Types, Springer LNCS, vol. 173, 145–156.CrossRefGoogle Scholar
Sato, M. and Garrigue, J. (2016). An intuitionistic set-theoretical model of CCω . Journal of Information Processing 24 (4) 711–720.CrossRefGoogle Scholar
Stefanova, M. and Geuvers, H. (1995). A simple model construction for the calculus of constructions. In: International Workshop on Types for Proofs and Programs.Google Scholar
Streicher, T. (1991). Semantics of Type Theory: Correctness, Completeness and Independence Results, Boston, MA, Birkäuser.CrossRefGoogle Scholar
Timany, A. and Sozeau, M. (2017). Consistency of the predicative calculus of cumulative inductive constructions (pCuIC). coRR. arXiv preprint arXiv:1710.03912.Google Scholar
Univalent Foundations Program (2013). Homotopy Type Theory: Univalent Foundations of Mathematics. http://homotopytypetheory.org/book, Institute for Advanced Study.Google Scholar
van Dalen, D. (1984). Intuitionistic logic. In: Handbook of Philosophical Logic, Volume III, Springer, 225–339.Google Scholar
van den Berg, B. (2007). Diaconescu’s theorem and the principle of propositional extensionality (Unpublished).Google Scholar
Werner, B. (1997). Sets in types, types in sets. In: Theoretical Aspects of Computer Software, Springer LNCS, vol. 1281, 530–546.CrossRefGoogle Scholar
Werner, B. (2008). On the strength of proof-irrelevant type theories. Logical Methods in Computer Science 4 (3:13) 1–20.Google Scholar