No CrossRef data available.
Article contents
Local Yoneda completions of quasi-metric spaces
Published online by Cambridge University Press: 24 March 2023
Abstract
In this paper, we study quasi-metric spaces using domain theory. Given a quasi-metric space (X,d), we use
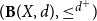 $({\bf B}(X,d),\leq^{d^{+}}\!)$
to denote the poset of formal balls of the associated quasi-metric space (X,d). We introduce the notion of local Yoneda-complete quasi-metric spaces in terms of domain-theoretic properties of
$({\bf B}(X,d),\leq^{d^{+}}\!)$
to denote the poset of formal balls of the associated quasi-metric space (X,d). We introduce the notion of local Yoneda-complete quasi-metric spaces in terms of domain-theoretic properties of
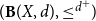 $({\bf B}(X,d),\leq^{d^{+}}\!)$
. The manner in which this definition is obtained is inspired by Romaguera–Valero theorem and Kostanek–Waszkiewicz theorem. Furthermore, we obtain characterizations of local Yoneda-complete quasi-metric spaces via local nets in quasi-metric spaces. More precisely, we prove that a quasi-metric space is local Yoneda-complete if and only if every local net has a d-limit. Finally, we prove that every quasi-metric space has a local Yoneda completion.
$({\bf B}(X,d),\leq^{d^{+}}\!)$
. The manner in which this definition is obtained is inspired by Romaguera–Valero theorem and Kostanek–Waszkiewicz theorem. Furthermore, we obtain characterizations of local Yoneda-complete quasi-metric spaces via local nets in quasi-metric spaces. More precisely, we prove that a quasi-metric space is local Yoneda-complete if and only if every local net has a d-limit. Finally, we prove that every quasi-metric space has a local Yoneda completion.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
This work is supported by the National Natural Science Foundation of China (Grant Nos. 12101383, 11871320, 11531009) and the Fundamental Research Funds for the Central Universities (Grant No. GK202103006).





