Hostname: page-component-7479d7b7d-jwnkl Total loading time: 0 Render date: 2024-07-09T22:25:32.699Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON ORDER-TYPE HOMOGENEOUS POINT SETS

Part of: Extremal combinatorics Polytopes and polyhedra General convexity

Published online by Cambridge University Press:  19 December 2013

Andrew Suk
Andrew Suk*
Affiliation:
Massachusetts Institute of Technology, Cambridge, MA,U.S.A. email asuk@math.mit.edu
Get access

Abstract

Let 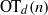${\mathrm{OT} }_{d} (n)$ be the smallest integer 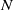$N$ such that every 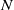$N$-element point sequence in 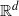${ \mathbb{R} }^{d} $ in general position contains an order-type homogeneous subset of size $n$, where a set is order-type homogeneous if all 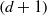$(d+ 1)$-tuples from this set have the same orientation. It is known that a point sequence in 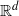${ \mathbb{R} }^{d} $ that is order-type homogeneous, forms the vertex set of a convex polytope that is combinatorially equivalent to a cyclic polytope in 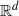${ \mathbb{R} }^{d} $. Two famous theorems of Erdős and Szekeres from 1935 imply that 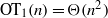${\mathrm{OT} }_{1} (n)= \Theta ({n}^{2} )$ and 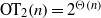${\mathrm{OT} }_{2} (n)= {2}^{\Theta (n)} $. For 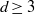$d\geq 3$, we give new bounds for 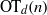${\mathrm{OT} }_{d} (n)$. In particular, we show that 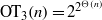${\mathrm{OT} }_{3} (n)= {2}^{{2}^{\Theta (n)} } $, answering a question of Eliáš and Matoušek, and, for 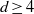$d\geq 4$, we show that 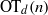${\mathrm{OT} }_{d} (n)$ is bounded above by an exponential tower of height 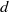$d$ with 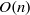$O(n)$ in the topmost exponent.

MSC classification

Secondary: 05D10: Ramsey theory 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52B11: $n$-dimensional polytopes
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 37 - 42
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Conlon, D., Fox, J., Pach, J., Sudakov, B. and Suk, A., Ramsey-type results on semi-algebraic relations, Trans. Amer. Math. Soc. (to appear).Google Scholar
Cordovil, R. and Duchet, P., Cyclic polytopes and oriented matroids. European J. Combin. 21 (2000), 49–64.CrossRefGoogle Scholar
Eliáš, M. and Matoušek, J., Higher-order Erdős–Szekeres theorems. Adv. Math. 244 (2013), 1–15.CrossRefGoogle Scholar
Erdős, P., Some remarks on the theory of graphs. Bull. Amer. Math. Soc. 53 (1947), 292–294.Google Scholar
Erdős, P., Hajnal, A. and Rado, R., Partition relations for cardinal numbers. Acta Math. Acad. Sci. Hungar. 16 (1965), 93–196.Google Scholar
Erdős, P. and Rado, R., Combinatorial theorems on classifications of subsets of a given set. Proc. Lond. Math. Soc. 3 (1952), 417–439.Google Scholar
Erdős, P. and Szekeres, G., A combinatorial problem in geometry. Compositio Math. 2 (1935), 463–470.Google Scholar
Erdős, P. and Szekeres, G., On some extremum problems in elementary geometry. Ann. Universitatis Scientiarum Budapestinensis, Eötvös, Sectio Mathematica 3/4 (1960–1961), 53–62.Google Scholar
Goodman, J. E. and Pollack, R., Allowable sequences and order types in discrete and computational geometry. In New Trends in Discrete and Computational Geometry (Algorithms and Combinatorics 10) (ed. Pach, J.),Springer (Berlin, 1993), 103–134.Google Scholar
Graham, R. L., Rothschild, B. L. and Spencer, J. H., Ramsey Theory, 2nd edn., Wiley (New York, 1990).Google Scholar
Grünbaum, B., Convex Polytopes, 2nd edn(Graduate Texts in Mathematics 221), Springer (2003).Google Scholar
Hubard, A., Montejano, L., Mora, E. and Suk, A., Order types of convex bodies. Order 28 (2011), 121–130.CrossRefGoogle Scholar
Matoušek, J., Lectures on Discrete Geometry, Springer (New York, 2002).CrossRefGoogle Scholar
McMullen, P., The maximal number of faces of a convex polytope. Mathematika 17 (1970), 179–184.Google Scholar
Moshkovitz, G. and Shapira, A., Ramsey theory, integer partitions and a new proof of the Erdős–Szekeres theorem. Preprint, 2012, arXiv:1206.4001.Google Scholar
Steele, M. J., Variations on the monotone subsequence theme of Erdős and Szekeres. In Discrete Probability and Algorithms (IMA Volumes in Mathematics and its Applications 72) (eds Aldous, D. et al. ),Springer (Berlin, 1995), 111–131.Google Scholar