Introduction
Scanning transmission electron microscopy (STEM) is one of the most powerful tools for inspecting materials with sub-nanometer or even sub-angstrom-level resolution. By scanning with a sharply focused electron probe, the information of the sample from each scan position is collected and images that contain features at the atomic level are generated. There are several methods to form images using the data collected from such experiments. Traditionally, detectors that capture electrons from certain ranges of scattering angles are used in the microscope. They generate a value based on the sum of received electrons at each probe position and result in 2D images. Images formed by detectors that collect signals at high scattering angles are even capable of detecting the scattering power experienced by the electron probe at the corresponding probe position (Pennycook, Reference Pennycook1989).
A pixelated detector does not generate a single value, but instead records a convergent beam electron diffraction (CBED) pattern for each probe position by using a large number of pixels, where each pixel can be seen as an individual detector. This results in a 4D dataset (2D CBED patterns on a 2D scan grid). More importantly, these advanced direct electron detectors (Müller et al., Reference Müller, Ryll, Ordavo, Ihle, Strüder, Volz, Zweck, Soltau and Rosenauer2012; Plackett et al., Reference Plackett, Horswell, Gimenez, Marchal, Omar and Tartoni2013; Tate et al., Reference Tate, Purohit, Chamberlain, Nguyen, Hovden, Chang, Deb, Turgut, Heron, Schlom and Ralph2016) record CBED patterns at a much higher rate than traditional charge-coupled device detectors and allow collecting a regular-sized 4D dataset before a serious sample drift can happen.
To process 4D datasets, one can define virtual detectors by selecting specific groups of pixels on the detector plane for summation, which result in similar 2D images to those of traditional detectors or seek solutions from more advanced and complex methods. Most of these methods take into account the distribution of the electrons on the detector plane, as well as the relationship between CBED patterns and their corresponding probe positions, allowing extra information to be extracted from the dataset. This enables reconstructions with resolution beyond the limitation imposed by the optical system (Nellist et al., Reference Nellist, McCallum and Rodenburg1995) and can reduce the dose needed for microscopists to obtain the necessary information to analyze their samples. Within the category of 4D dataset processing methods, iterative optimization approaches (Rodenburg & Faulkner, Reference Rodenburg and Faulkner2004; Maiden & Rodenburg, Reference Maiden and Rodenburg2009; Odstrčil et al., Reference Odstrčil, Menzel and Guizar-Sicairos2018; Chen et al., Reference Chen, Odstrcil, Jiang, Han, Chiu, Li and Muller2020, Reference Chen, Jiang, Shao, Holtz, Odstrčil, Guizar-Sicairos, Hanke, Ganschow, Schlom and Muller2021) reconstruct subsets of the full dataset one region at a time. The process repeats and reprocesses each subset until the algorithm converges to an estimated version of electric potential distribution. Other methods that handle 4D datasets without an iterative process, for example, single sideband ptychography (SSB) (Pennycook et al., Reference Pennycook, Lupini, Yang, Murfitt, Jones and Nellist2015; Yang et al., Reference Yang, Pennycook and Nellist2015), or integrated center of mass (iCOM) or integrated differential phase contrast (iDPC) (Müller et al., Reference Müller, Krause, Béché, Schowalter, Galioit, Löffler, Verbeeck, Zweck, Schattschneider and Rosenauer2014; Yang et al., Reference Yang, Pennycook and Nellist2015; Lazić et al., Reference Lazić, Bosch and Lazar2016; Yücelen et al., Reference Yücelen, Lazić and Bosch2018) reconstruction methods, have also proved to be much more dose efficient than traditional imaging methods. Compared with iterative processes, they are less computationally demanding and guarantee unique solutions since they do not depend on optimization algorithms. Also, some prior knowledge, such as the prediction of a phase distribution that may arise from astigmatism and defocus, can be provided to this post process for acquiring more detailed information (Pelz et al., Reference Pelz, Johnson, Ophus, Ercius and Scott2021). However, the ability to achieve fast reconstructions, regardless whether they are iterative or not, usually relies on accelerators (e.g., GPUs), as well as large amounts of computer memory in order to accommodate the whole dataset, or some reduced version of it. With an exception of iCOM, most of these post processing methods are thus limited by the hardware to a certain number of probe positions.
Even though the reconstruction methods may be further optimized to reduce the processing time, users still need to wait for the recording of the dataset to be completed before a resulting image can be generated. This waiting time varies, but for datasets composed of a large number of scan points or in situations where the detector has a slow frame rate, this delay would hinder the process of searching for features of interest, as well as adjusting the optical system based on the observations. Some rather simple approaches, such as traditional imaging methods, COM shift, or some of its derivatives such as COM shift divergence (Haas et al., Reference Haas, Mittelberger, Meyer, Plotkin-Swing, Dellby, Krivanek, Lovejoy and Koch2021), can effectively reduce or eliminate this delay. However, these methods also require a higher number of electrons to generate images with adequate quality, compared with more complex methods such as SSB, iCOM, and iDPC. As proposed by Strauch et al. (Reference Strauch, Weber, Clausen, Lesnichaia, Bangun, März, Lyu, Chen, Rosenauer, Dunin-Borkowski and Müller-Caspary2021), a dose-efficient reconstruction with live image update can be done by first allocating memory for the dataset and then gradually filling it with collected and processed data during the scanning process. An update of the reconstructed image can be generated anytime by SSB reconstruction, even before the dataset is complete. However, this also indicates that the number of probe positions in a dataset is limited by the GPU memory, as it needs to store data for later processing. At the current state of technology, this approach is limited in terms of processing rate to about 1,000 probe positions per second in the implementation of Strauch et al. (Reference Strauch, Weber, Clausen, Lesnichaia, Bangun, März, Lyu, Chen, Rosenauer, Dunin-Borkowski and Müller-Caspary2021), while the collection frame rate of direct electron detectors is approaching 100 kHz (Pelz et al., Reference Pelz, Johnson, Ophus, Ercius and Scott2021) and even the MHz range for event-driven cameras at suitable conditions (Jannis et al., Reference Jannis, Hofer, Gao, Xie, Béché, Pennycook and Verbeeck2021).
To overcome these hardware and speed limitations, we hereby propose a new live reconstruction method based on iCOM, which does not rely on storing the entire 4D dataset in memory, does not require accelerators of any kind, and thus greatly reduces the computational requirements, as well as allowing reconstructions of images of a larger scale. In this paper, the physical formulation of real-time iCOM (riCOM) is first derived, and details of the software implementation of the reconstruction algorithm are discussed. This software implements a direct interface to the electron camera, and several real-time reconstructed results are recorded, from which one can see that the tuning of the imaging conditions is immediately reflected in live-updated images. RiCOM reconstruction from existing experimental datasets is also shown. These datasets are recorded frame-by-frame or per-event (Guo et al., Reference Guo, Franken, Deng, Benlekbir, Singla Lezcano, Janssen, Yu, Ripstein, Tan and Rubinstein2020; Jannis et al., Reference Jannis, Hofer, Gao, Xie, Béché, Pennycook and Verbeeck2021). Both formats can be processed with the riCOM method with little alteration of the algorithm. Reconstruction results with different ranges of integration and integrated filters are also displayed. They are compared with each other and with other reconstruction methods to put the proposed method into context.
Methods
Physical Formulation
In 4D STEM, the distribution of the electron intensity at each probe position is recorded. The COM of this distribution can then be calculated, resulting in a vector image ![]() $\vec {I}^{{\rm COM}}( \vec {r}_p)$ or two scalar images describing its
$\vec {I}^{{\rm COM}}( \vec {r}_p)$ or two scalar images describing its ![]() $x$ component
$x$ component ![]() $I^{{\rm COM}x}( \vec {r}_p)$ and
$I^{{\rm COM}x}( \vec {r}_p)$ and ![]() $y$ component
$y$ component ![]() $I^{{\rm COM}y}( \vec {r}_p)$ . For the
$I^{{\rm COM}y}( \vec {r}_p)$ . For the ![]() $x$-component,
$x$-component,
where ![]() $\vec {r}_p$ is the probe position,
$\vec {r}_p$ is the probe position, ![]() $\vec {k}$ indicates a point on the detector plane with components
$\vec {k}$ indicates a point on the detector plane with components ![]() $k_x$ and
$k_x$ and ![]() $k_y$, and
$k_y$, and ![]() $I( \vec {k},\; \vec {r}_p)$ is the intensity at
$I( \vec {k},\; \vec {r}_p)$ is the intensity at ![]() $\vec {k}$ while the probe is situated at
$\vec {k}$ while the probe is situated at ![]() $\vec {r}_p$. From previous work (Lazić et al., Reference Lazić, Bosch and Lazar2016), it follows that (derivation in the Supplementary Material)
$\vec {r}_p$. From previous work (Lazić et al., Reference Lazić, Bosch and Lazar2016), it follows that (derivation in the Supplementary Material)
 $$\eqalign{\vec{I}^{{\rm COM}}( \vec{r}_p) & = {1\over 2}\vert \psi_{\rm in}( \vec{r},\; \vec{r}_p) \vert ^{2}\star\nabla\phi( \vec{r}) \cr & = {1\over 2}\nabla( \vert \psi_{\rm in}( \vec{r},\; \vec{r}_p) \vert ^{2}\star\phi( \vec{r}) ) \cr & = \nabla O( \vec{r}_p) .}$$
$$\eqalign{\vec{I}^{{\rm COM}}( \vec{r}_p) & = {1\over 2}\vert \psi_{\rm in}( \vec{r},\; \vec{r}_p) \vert ^{2}\star\nabla\phi( \vec{r}) \cr & = {1\over 2}\nabla( \vert \psi_{\rm in}( \vec{r},\; \vec{r}_p) \vert ^{2}\star\phi( \vec{r}) ) \cr & = \nabla O( \vec{r}_p) .}$$ In equation (2), the COM shift signal is understood as the gradient (![]() $\nabla$) of a function
$\nabla$) of a function ![]() $O( \vec {r}_p)$, which is the local projected potential
$O( \vec {r}_p)$, which is the local projected potential ![]() $\phi ( \vec {r})$ cross-correlated (
$\phi ( \vec {r})$ cross-correlated (![]() $\star$) with the intensity distribution of the incoming electron beam at a given probe position
$\star$) with the intensity distribution of the incoming electron beam at a given probe position ![]() $\vert \psi _{\rm in}( \vec {r},\; \vec {r}_p) \vert ^{2}$. Note that this result is achieved under the phase object approximation, which assumes that the electron probe remains unmodified while passing through the object. With this approximation, the 3D potential established by the material is simplified to a projected potential in a 2D plane. It clearly fails for thicker objects, but it allows a simple derivation and easy understanding of how experimental conditions can affect reconstructed images.
$\vert \psi _{\rm in}( \vec {r},\; \vec {r}_p) \vert ^{2}$. Note that this result is achieved under the phase object approximation, which assumes that the electron probe remains unmodified while passing through the object. With this approximation, the 3D potential established by the material is simplified to a projected potential in a 2D plane. It clearly fails for thicker objects, but it allows a simple derivation and easy understanding of how experimental conditions can affect reconstructed images.
To solve for a scalar function describing the object, path integration is performed on the COM shift signal to remove the gradient from the right-hand side of equation (2). For an ideal case, the path of the integration can be taken arbitrarily, since the integral is only dependent on the end point of the path integration. However, in realistic cases, the measurement of COM shift contains noise, and thus it would give better estimation of the noise-free result by taking the average of all possible path integrals. By the assumption that equipotential can be found at infinity, this can be achieved by averaging path integrals at all possible azimuthal angles, from infinity toward the probe position. In order for this concept to work with a 2D grid of probe positions, the averaged integral can be expressed in a discretized form:
 $$\eqalign{& O( \vec{r}_p) \cr & \quad = \int_{\infty}^{\vec{r}_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r} \cr & \quad = {1\over 2\pi} \int_{0}^{2\pi} \int_{\infty}^{r_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot \hat{n} \, {d}r \, {d}\theta \cr & = {a\over 2\pi} \sum_{x = -\infty}^{ + \infty} \sum_{y = -\infty}^{ + \infty} {\vec{r}_p-\vec{r}_{xy}\over \vert \vec{r}_p-\vec{r}_{xy}\vert ^{2}} \cdot \vec{I}^{{\rm COM}}( \vec{r}_{xy}) .}$$
$$\eqalign{& O( \vec{r}_p) \cr & \quad = \int_{\infty}^{\vec{r}_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r} \cr & \quad = {1\over 2\pi} \int_{0}^{2\pi} \int_{\infty}^{r_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot \hat{n} \, {d}r \, {d}\theta \cr & = {a\over 2\pi} \sum_{x = -\infty}^{ + \infty} \sum_{y = -\infty}^{ + \infty} {\vec{r}_p-\vec{r}_{xy}\over \vert \vec{r}_p-\vec{r}_{xy}\vert ^{2}} \cdot \vec{I}^{{\rm COM}}( \vec{r}_{xy}) .}$$ In the continuous representation of the radial averaged path integral (third line of equation (3)), ![]() $\hat {n}$ is a unit vector pointing toward
$\hat {n}$ is a unit vector pointing toward ![]() $\vec {r}_p$. In the discrete representation (fourth line of equation (3)),
$\vec {r}_p$. In the discrete representation (fourth line of equation (3)), ![]() $\vec {r}_{xy}$ describes a vector pointing at each probe position that composes the 2D array, and
$\vec {r}_{xy}$ describes a vector pointing at each probe position that composes the 2D array, and ![]() $a$ describes a factor proportional to the square of the step size taken to discretize the integration.
$a$ describes a factor proportional to the square of the step size taken to discretize the integration.
The discrete representation in equation (3) states that the summation has to go over an infinite amount of points, or at least all probe positions in the dataset (as for iCOM reconstructions) in order to acquire or to approximate the desired object function. This would require the full dataset to be collected first, and rendering a live update of the partially reconstructed dataset is therefore impossible. However, it is found that by limiting the spatial range of the summation, the algorithm results in similar reconstructions as iCOM, but with more emphasis on local variations of the object function. This behavior can be understood qualitatively. The term ![]() $( \vec {r}_p-\vec {r}_{xy}) /\vert \vec {r}_p-\vec {r}_{xy}\vert ^{2}$ describes an odd function since the vector distribution on both sides of the probe position
$( \vec {r}_p-\vec {r}_{xy}) /\vert \vec {r}_p-\vec {r}_{xy}\vert ^{2}$ describes an odd function since the vector distribution on both sides of the probe position ![]() $\vec {r}_p$ is the same in magnitude but opposite in the direction as the sign changes for
$\vec {r}_p$ is the same in magnitude but opposite in the direction as the sign changes for ![]() $\vec {r}_p-\vec {r}_{xy}$. For a global homogeneous COM shift, or for cases where the variation is negligible within the range of the kernel size, it results in an even function for
$\vec {r}_p-\vec {r}_{xy}$. For a global homogeneous COM shift, or for cases where the variation is negligible within the range of the kernel size, it results in an even function for ![]() $\vec {I}^{{\rm COM}}( \vec {r}_{xy})$, and thus the sum of the product of the two will always be zero. But for short-range variations of the object function, which results in local fluctuations of the
$\vec {I}^{{\rm COM}}( \vec {r}_{xy})$, and thus the sum of the product of the two will always be zero. But for short-range variations of the object function, which results in local fluctuations of the ![]() $\vec {I}^{{\rm COM}}$ distribution, it would generate non-zero contribution to the summation result. By replacing the infinite sum in equation (3) with a finite sum considering a kernel of
$\vec {I}^{{\rm COM}}$ distribution, it would generate non-zero contribution to the summation result. By replacing the infinite sum in equation (3) with a finite sum considering a kernel of ![]() $n \times n$ pixels, it results in:
$n \times n$ pixels, it results in:
 $$\eqalign{& I^{{\rm riCOM}}( \vec{r}_p) \cr & \quad = {a\over 2\pi} \sum_{x = r_{\,p, x}-{n-1\over 2}}^{r_{\,p, x} + {n-1\over 2}} \sum_{y = r_{\,p, y}-{n-1\over 2}}^{r_{\,p, y} + {n-1\over 2}} {\vec{r}_p-\vec{r}_{xy}\over \vert \vec{r}_p-\vec{r}_{xy}\vert ^{2}} \cdot \vec{I}^{{\rm COM}}( \vec{r}_{xy}) \cr & \quad = k_n( \vec{r}_p) \star \vec{I}^{{\rm COM}}( \vec{r}_{\,p}) \cr & k_n( \vec{r}_p) = {a\over 2\pi} \sum_{x = r_{\,p, x}-{n-1\over 2}}^{r_{\,p, x} + {n-1\over 2}} \sum_{y = r_{\,p, y}-{n-1\over 2}}^{r_{\,p, y} + {n-1\over 2}} {\vec{r}_p-\vec{r}_{xy}\over \vert \vec{r}_p-\vec{r}_{xy}\vert ^{2}}.}$$
$$\eqalign{& I^{{\rm riCOM}}( \vec{r}_p) \cr & \quad = {a\over 2\pi} \sum_{x = r_{\,p, x}-{n-1\over 2}}^{r_{\,p, x} + {n-1\over 2}} \sum_{y = r_{\,p, y}-{n-1\over 2}}^{r_{\,p, y} + {n-1\over 2}} {\vec{r}_p-\vec{r}_{xy}\over \vert \vec{r}_p-\vec{r}_{xy}\vert ^{2}} \cdot \vec{I}^{{\rm COM}}( \vec{r}_{xy}) \cr & \quad = k_n( \vec{r}_p) \star \vec{I}^{{\rm COM}}( \vec{r}_{\,p}) \cr & k_n( \vec{r}_p) = {a\over 2\pi} \sum_{x = r_{\,p, x}-{n-1\over 2}}^{r_{\,p, x} + {n-1\over 2}} \sum_{y = r_{\,p, y}-{n-1\over 2}}^{r_{\,p, y} + {n-1\over 2}} {\vec{r}_p-\vec{r}_{xy}\over \vert \vec{r}_p-\vec{r}_{xy}\vert ^{2}}.}$$ Equation (4) shows the summation with a range ![]() $n$ centered at the probe position
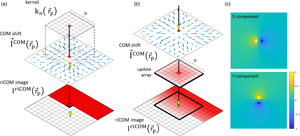
$n$ centered at the probe position ![]() $\vec {r}_p = ( r_{p, x},\; r_{p, y})$. With this constraint on the range, the iCOM at one point can be found by only processing COM data from its limited surrounding (Fig. 1a), allowing data processing to begin and results to be generated during the scanning session. This reconstruction method is thus given the name “real-time iCOM” or “riCOM,” as indicated in the same equation by
$\vec {r}_p = ( r_{p, x},\; r_{p, y})$. With this constraint on the range, the iCOM at one point can be found by only processing COM data from its limited surrounding (Fig. 1a), allowing data processing to begin and results to be generated during the scanning session. This reconstruction method is thus given the name “real-time iCOM” or “riCOM,” as indicated in the same equation by ![]() $I^{{\rm riCOM}}( \vec {r}_p)$. This process is equivalent to a cross-correlation between an array
$I^{{\rm riCOM}}( \vec {r}_p)$. This process is equivalent to a cross-correlation between an array ![]() $k_n( \vec {r}_p)$ of size
$k_n( \vec {r}_p)$ of size ![]() $n\times n$ that stores vectors
$n\times n$ that stores vectors ![]() $( \vec {r}_p-\vec {r}_{xy}) /\vert \vec {r}_p-\vec {r}_{xy}\vert ^{2}$ and the COM shift map
$( \vec {r}_p-\vec {r}_{xy}) /\vert \vec {r}_p-\vec {r}_{xy}\vert ^{2}$ and the COM shift map ![]() $\vec {I}^{{\rm COM}}( \vec {r}_{xy})$. This array will be referred to as the “kernel” throughout this manuscript, and images generated by processing COM shift maps with such kernels will be denoted as “riCOM results’ or “riCOM images.”
$\vec {I}^{{\rm COM}}( \vec {r}_{xy})$. This array will be referred to as the “kernel” throughout this manuscript, and images generated by processing COM shift maps with such kernels will be denoted as “riCOM results’ or “riCOM images.”
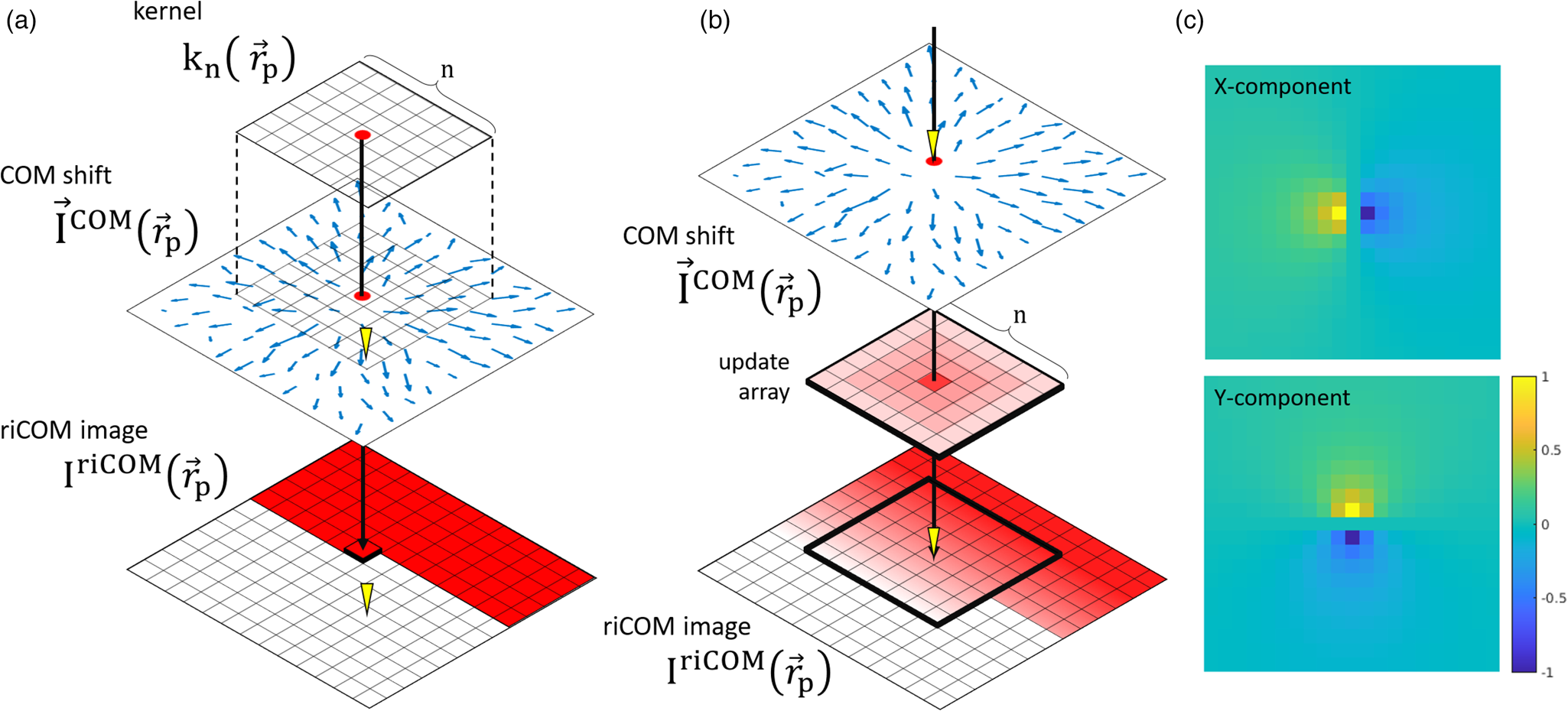
Fig. 1. (a) The kernel takes multiple data points from the COM shift map to calculate the value for one pixel in the riCOM image. (b) The riCOM image is being updated based on the contributions of the COM shift at one probe position. The yellow triangles indicate the scanning probe position. (c) ![]() $X$ and
$X$ and ![]() $Y$ components of a kernel of size
$Y$ components of a kernel of size ![]() $21\times 21$.
$21\times 21$.
Since the kernel processes a group of data points and outputs a value corresponding to the probe position at the center of the kernel, the collection of data has to lead the reconstruction by ![]() $( n-1) /2$ scan lines to fill up the kernel (when scanning in a traditional line by line fashion). This delay between the data collection progress and reconstruction result can be troublesome for operations that highly rely on real-time feedback from the scanning process. Since the summation in equation (4) describes a linearly independent process, the contribution from multiple probe positions to a common pixel in the riCOM array can be separately calculated. Furthermore, by collecting the contribution from the COM shift at a specific probe position to its vicinity, an update to the riCOM image can be generated in the form of an array of the same size as the kernel. Since this reconstruction scheme depends on one CBED pattern at a time, it leads to a live update of the riCOM result without any delay (Fig. 1b). Although this does not reduce the time differences between the latest scanning point and the fully updated riCOM pixel, the partially reconstructed fraction of the riCOM image can already show atomic features,Footnote 1 and therefore, valuable information at the newly scanned probe position appears with minimal delay. This way the user can also get a quick feedback of their operation. Another advantage is that once the contribution from one probe position is calculated and the corresponding update to the riCOM array is made, the CBED pattern can be discarded, freeing up memory. This effectively removes any memory imposed restriction on scan size if the user is only interested in the resulting riCOM image.
$( n-1) /2$ scan lines to fill up the kernel (when scanning in a traditional line by line fashion). This delay between the data collection progress and reconstruction result can be troublesome for operations that highly rely on real-time feedback from the scanning process. Since the summation in equation (4) describes a linearly independent process, the contribution from multiple probe positions to a common pixel in the riCOM array can be separately calculated. Furthermore, by collecting the contribution from the COM shift at a specific probe position to its vicinity, an update to the riCOM image can be generated in the form of an array of the same size as the kernel. Since this reconstruction scheme depends on one CBED pattern at a time, it leads to a live update of the riCOM result without any delay (Fig. 1b). Although this does not reduce the time differences between the latest scanning point and the fully updated riCOM pixel, the partially reconstructed fraction of the riCOM image can already show atomic features,Footnote 1 and therefore, valuable information at the newly scanned probe position appears with minimal delay. This way the user can also get a quick feedback of their operation. Another advantage is that once the contribution from one probe position is calculated and the corresponding update to the riCOM array is made, the CBED pattern can be discarded, freeing up memory. This effectively removes any memory imposed restriction on scan size if the user is only interested in the resulting riCOM image.
Kernel Design
As mentioned in the previous section, summation carried out by a smaller kernel emphasizes local object function variations. In other words, it gives more weights to components of higher spatial frequency. To show the relationship between this effect and the kernel size, we start with the Fourier transform of the function ![]() $O( \vec {r}_p)$ for the case of a perfect COM shift measurement (the second line of equation (3)).
$O( \vec {r}_p)$ for the case of a perfect COM shift measurement (the second line of equation (3)).
 $$\eqalign{{\cal F} { O( \vec{r}_p) } & = {\cal F} \left\{\int_{-\infty}^{\vec{r}_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r}\right\}\cr & = {\cal F} { \vec{I}^{{\rm COM}}( \vec{r}_p) } \cdot {1\over i\vec{k}_p}.}$$
$$\eqalign{{\cal F} { O( \vec{r}_p) } & = {\cal F} \left\{\int_{-\infty}^{\vec{r}_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r}\right\}\cr & = {\cal F} { \vec{I}^{{\rm COM}}( \vec{r}_p) } \cdot {1\over i\vec{k}_p}.}$$ Here the symbol ![]() ${\cal F}$ indicates Fourier transform and
${\cal F}$ indicates Fourier transform and ![]() $\vec {k}_p$ is a vector in the Fourier domain. As seen in equation (5), each of the Fourier components of the COM shift map is transferred to the final image with a weight
$\vec {k}_p$ is a vector in the Fourier domain. As seen in equation (5), each of the Fourier components of the COM shift map is transferred to the final image with a weight ![]() $1/i\vec {k}_p$ after the path integration. This transfer function decays fast with the frequency, and thus low-frequency components are attenuated much less than high-frequency ones. By integrating over a finite range, an analytical expression for the riCOM result can be obtained as follows:
$1/i\vec {k}_p$ after the path integration. This transfer function decays fast with the frequency, and thus low-frequency components are attenuated much less than high-frequency ones. By integrating over a finite range, an analytical expression for the riCOM result can be obtained as follows:
 $$\eqalign{& {\cal F} { I^{{\rm riCOM}}( \vec{r}_p) } \cr & \quad = {\cal F} \left\{\int_{\vec{r}_p-\Delta \vec{r}}^{\vec{r}_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r} - \int_{\vec{r}_p}^{\vec{r}_p + \Delta\vec{r}} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r}\right\}/2 \cr & \quad = {\cal F} { \vec{I}^{{\rm COM}}( \vec{r}_p) } \cdot {1\over i\vec{k}_p}\times[ 1-\cos( \Delta\vec{r}\cdot\vec{k}_p) ] \cr & \quad = {\cal F}{ O( \vec{r}_p) } \times[ 1-\cos( \Delta\vec{r}\cdot\vec{k}_p) ] .}$$
$$\eqalign{& {\cal F} { I^{{\rm riCOM}}( \vec{r}_p) } \cr & \quad = {\cal F} \left\{\int_{\vec{r}_p-\Delta \vec{r}}^{\vec{r}_p} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r} - \int_{\vec{r}_p}^{\vec{r}_p + \Delta\vec{r}} \vec{I}^{{\rm COM}}( \vec{r}) \cdot {d}\vec{r}\right\}/2 \cr & \quad = {\cal F} { \vec{I}^{{\rm COM}}( \vec{r}_p) } \cdot {1\over i\vec{k}_p}\times[ 1-\cos( \Delta\vec{r}\cdot\vec{k}_p) ] \cr & \quad = {\cal F}{ O( \vec{r}_p) } \times[ 1-\cos( \Delta\vec{r}\cdot\vec{k}_p) ] .}$$ In equation (6), the riCOM result is approximated by the contribution from both sides of the probe position ![]() $\vec {r}_p$ in a single line, within the range of
$\vec {r}_p$ in a single line, within the range of ![]() $2\Delta \vec {r}$. The result shows that by limiting the integration range, it reproduces the function
$2\Delta \vec {r}$. The result shows that by limiting the integration range, it reproduces the function ![]() $O( \vec {r}_p)$ with an extra weighting function
$O( \vec {r}_p)$ with an extra weighting function ![]() $1-\cos ( \Delta \vec {r}\cdot \vec {k}_p)$. This function is close to zero when
$1-\cos ( \Delta \vec {r}\cdot \vec {k}_p)$. This function is close to zero when ![]() $\Delta \vec {r}\cdot \vec {k}_p$ is small, and thus strongly suppresses the low-frequency signal in the retrieved object function. Also, it peaks at
$\Delta \vec {r}\cdot \vec {k}_p$ is small, and thus strongly suppresses the low-frequency signal in the retrieved object function. Also, it peaks at ![]() $\vec {k}_p = {\pi }/{\Delta \vec {r}}$, which implies that by choosing smaller
$\vec {k}_p = {\pi }/{\Delta \vec {r}}$, which implies that by choosing smaller ![]() $\Delta \vec {r}$, or shorter integration range, one can put more weight to the high-frequency components. By using kernels with sizes smaller than the real-space dimension of the dataset, this effect of limiting integration range can be achieved. Although the actual frequency spectrum of a 2D kernel deviates, the weight of a kernel of size
$\Delta \vec {r}$, or shorter integration range, one can put more weight to the high-frequency components. By using kernels with sizes smaller than the real-space dimension of the dataset, this effect of limiting integration range can be achieved. Although the actual frequency spectrum of a 2D kernel deviates, the weight of a kernel of size ![]() $n$ at each frequency
$n$ at each frequency ![]() $k$ can be well approximated with the formula derived from line-integration:
$k$ can be well approximated with the formula derived from line-integration:
Here ![]() $N$ is the number of pixels of the image in one direction, and the extra factor
$N$ is the number of pixels of the image in one direction, and the extra factor ![]() $2\pi /N$ scales with the pixel size in the Fourier transformed result.
$2\pi /N$ scales with the pixel size in the Fourier transformed result.
This effect is not equal to but can be compared with a high-pass filter as it emphasizes high-frequency details in the reconstructed image. However, other filtering effects, such as low-pass or band-pass filtering, cannot be created simply by altering the kernel size. A filter can be seen as a mask that reduces or eliminates a certain range of frequency signals of an image. This is done by a piece-wise multiplication between the filter and the image in the frequency domain, which is equivalent to a convolution between their real-space counterparts. For riCOM images, which can be seen as a cross-correlation between a COM shift map and a kernel, the application of such a filter can be included to the design of the kernel:
 $$\eqalign{I^{{\rm riCOM}}( \vec{r}_p) \ast f( \vec{r}_p) & = [ \vec{I}^{{\rm COM}}( \vec{r}_p) \star k_n( \vec{r}_p) ] \ast f( \vec{r}_p) \cr & = \vec{I}^{{\rm COM}}( \vec{r}_p) \star [ k_n( \vec{r}_p) \ast f( \vec{r}_p) ] .}$$
$$\eqalign{I^{{\rm riCOM}}( \vec{r}_p) \ast f( \vec{r}_p) & = [ \vec{I}^{{\rm COM}}( \vec{r}_p) \star k_n( \vec{r}_p) ] \ast f( \vec{r}_p) \cr & = \vec{I}^{{\rm COM}}( \vec{r}_p) \star [ k_n( \vec{r}_p) \ast f( \vec{r}_p) ] .}$$With
 $$\matrix{\,f( \vec{r}_p) ) & = {\cal F}^{-1} { F( \vec{k}_p) } \cr F( \vec{k}_p) & = \left\{\matrix{ 1,\; \hfill & k_{{\rm max}} \geq \vert k_p\vert \geq k_{{\rm min}}\hfill \cr 0,\; \hfill & {\rm otherwise} \hfill }\right. }.$$
$$\matrix{\,f( \vec{r}_p) ) & = {\cal F}^{-1} { F( \vec{k}_p) } \cr F( \vec{k}_p) & = \left\{\matrix{ 1,\; \hfill & k_{{\rm max}} \geq \vert k_p\vert \geq k_{{\rm min}}\hfill \cr 0,\; \hfill & {\rm otherwise} \hfill }\right. }.$$ In equation (8), ![]() $f( \vec {r}_p)$ is the filter function and the symbol
$f( \vec {r}_p)$ is the filter function and the symbol ![]() $\ast$ indicates convolution. Equation (9) writes one of the possible ways to design such a filter, with a hard cutoff at two frequency limits
$\ast$ indicates convolution. Equation (9) writes one of the possible ways to design such a filter, with a hard cutoff at two frequency limits ![]() $k_{{\rm max}}$ and
$k_{{\rm max}}$ and ![]() $k_{{\rm min}}$, that is, a band-pass filter. The real-space counterpart of the filter can be found by performing an inverse Fourier transform
$k_{{\rm min}}$, that is, a band-pass filter. The real-space counterpart of the filter can be found by performing an inverse Fourier transform ![]() ${\cal F}^{-1}$ to the filter function in the Fourier domain. This real-space filtering effect can be incorporated to the kernel due to the associative property of cross-correlation and convolution. It is worth noting that the last part of equation (8) only holds for centrally symmetric filters that treat frequency components at different azimuthal angles equally, which is indeed the case for the filter shown in equation (9). We also want to point out that to create a sharp cutoff at the frequency domain, one would need a filter matching the size of the COM shift array. But in order to keep the size of the kernel, the outcome of the convolution is reduced in size. In other words, the outcome of
${\cal F}^{-1}$ to the filter function in the Fourier domain. This real-space filtering effect can be incorporated to the kernel due to the associative property of cross-correlation and convolution. It is worth noting that the last part of equation (8) only holds for centrally symmetric filters that treat frequency components at different azimuthal angles equally, which is indeed the case for the filter shown in equation (9). We also want to point out that to create a sharp cutoff at the frequency domain, one would need a filter matching the size of the COM shift array. But in order to keep the size of the kernel, the outcome of the convolution is reduced in size. In other words, the outcome of ![]() $k( \vec {r}_p) \ast f( \vec {r}_p)$ is kept at the same size as
$k( \vec {r}_p) \ast f( \vec {r}_p)$ is kept at the same size as ![]() $k( \vec {r}_p)$. This would make the cutoff appears in the fashion of a slope and also distorts the rest of the frequency spectrum.
$k( \vec {r}_p)$. This would make the cutoff appears in the fashion of a slope and also distorts the rest of the frequency spectrum.
In Figure 2, the frequency components of different kernel designs are illustrated. From bottom to top, the curves correspond to the template kernel with the size of ![]() $101\times 101$, a smaller kernel with the size of
$101\times 101$, a smaller kernel with the size of ![]() $41\times 41$, and the template kernel with a high-pass filter (
$41\times 41$, and the template kernel with a high-pass filter (![]() $k_{{\rm min}} = {12.19\over 2}\ {\rm px}^{-1}$), a low-pass filter (
$k_{{\rm min}} = {12.19\over 2}\ {\rm px}^{-1}$), a low-pass filter (![]() $k_{{\rm max}} = 12.19\ {\rm px}^{-1}$), and a band-pass filter (
$k_{{\rm max}} = 12.19\ {\rm px}^{-1}$), and a band-pass filter (![]() $k_{{\rm min}},\; k_{{\rm max}}$ same as before). For the bottom two curves, the result of the corresponding line-integration approximation (dashed lines), with
$k_{{\rm min}},\; k_{{\rm max}}$ same as before). For the bottom two curves, the result of the corresponding line-integration approximation (dashed lines), with ![]() $\vec {\Delta \vec {r}}$ chosen to be half of the kernel size, is also drawn to show their similarity in oscillation frequency and magnitude.
$\vec {\Delta \vec {r}}$ chosen to be half of the kernel size, is also drawn to show their similarity in oscillation frequency and magnitude.

Fig. 2. Frequency components of a set of kernels acting on a COM shift map of size ![]() $500\times 500$. The presented examples include, from bottom to top, the template kernel with the size of
$500\times 500$. The presented examples include, from bottom to top, the template kernel with the size of ![]() $101\times 101$, a smaller kernel with the size of
$101\times 101$, a smaller kernel with the size of ![]() $41\times 41$, and the template kernel with a high-pass filter, a low-pass filter, and a band-pass filter. The dashed line shows the predicted transfer function with the line-integration approximation. The two vertical lines indicate the cutoff frequency of the filter or the inverse of the kernel size, and the circles at the intersection of the vertical lines and integral indicates whether a cutoff frequency is applied to the specific design.
$41\times 41$, and the template kernel with a high-pass filter, a low-pass filter, and a band-pass filter. The dashed line shows the predicted transfer function with the line-integration approximation. The two vertical lines indicate the cutoff frequency of the filter or the inverse of the kernel size, and the circles at the intersection of the vertical lines and integral indicates whether a cutoff frequency is applied to the specific design.
By comparing the blue and gray curves in Figure 2, it is clear that Kernel 41 peaks at a higher frequency than Kernel 101, as predicted by the analytical formula, and that the cutoff of the lower frequency due to a smaller kernel happens approximately at the inverse of the kernel size, as indicated in the gray circle. This value is then used for ![]() $k_{{\rm min}}$ of the high-pass filter incorporated to Kernel 101-HP (orange curve), which indeed shows a similar overall frequency spectrum as the one of Kernel 41. Note that the size reduction after convolution between kernel and the decorating filter causes a smooth decrease of frequency components below
$k_{{\rm min}}$ of the high-pass filter incorporated to Kernel 101-HP (orange curve), which indeed shows a similar overall frequency spectrum as the one of Kernel 41. Note that the size reduction after convolution between kernel and the decorating filter causes a smooth decrease of frequency components below ![]() $k_{{\rm min}}$, and the spectrum differences beyond
$k_{{\rm min}}$, and the spectrum differences beyond ![]() $k_{{\rm min}}$ compared with Kernel 101. Similarly, a kernel with a low-pass filter Kernel 101-LP (green curve) and a kernel incorporating a band-pass filter Kernel 101-BP (pink curve) are created. Both of them are showing a suppression of the higher frequency ranges. Kernel 101-BP also shows a shift of the spectrum peak to a higher frequency because of its high-pass characteristic.
$k_{{\rm min}}$ compared with Kernel 101. Similarly, a kernel with a low-pass filter Kernel 101-LP (green curve) and a kernel incorporating a band-pass filter Kernel 101-BP (pink curve) are created. Both of them are showing a suppression of the higher frequency ranges. Kernel 101-BP also shows a shift of the spectrum peak to a higher frequency because of its high-pass characteristic.
Despite the fact that it is not always possible to recreate the exact characteristics of common post-processing filters, the incorporation of filters into the kernel, as well as the choice of kernel sizes allows for a great flexibility for frequency tuning and yields consistent and predictable solutions. Combining the kernel and the filter in real space also enables these image processing functions to be applied before the complete riCOM image is rendered and thus compatible with the live update algorithm.
Data Processing
Due to the simplicity of the algorithm, the processing can be carried out completely by CPU with a very limited usage of memory. However, in order to reach real-time reconstruction that is limited only by the frame rate of the camera, an efficient implementation of the algorithm is crucial. The benchmark shown in Figure 3 shows that an optimized implementation using C++ can easily achieve the maximum speed of ![]() $\approx$14 kHz of a MerlinEM camera. Additionally, the pre-processing of binary live data benefits from the low-level features of C++ (e.g., adapting endianness and efficient conversion of binary into numerical arrays). An implementation of the algorithm tailored to event-driven cameras and their corresponding sparse datasets is even significantly faster. Depending on the dose, >100 kHz have been obtained. The live visualizations at such rates also benefit from using C++ through the possibility of directly accessing and modifying OpenGL textures across threads.
$\approx$14 kHz of a MerlinEM camera. Additionally, the pre-processing of binary live data benefits from the low-level features of C++ (e.g., adapting endianness and efficient conversion of binary into numerical arrays). An implementation of the algorithm tailored to event-driven cameras and their corresponding sparse datasets is even significantly faster. Depending on the dose, >100 kHz have been obtained. The live visualizations at such rates also benefit from using C++ through the possibility of directly accessing and modifying OpenGL textures across threads.

Fig. 3. Speed (frame rate in kHz) versus implementation benchmark for the computation of riCOM signal with the Kernel size of ![]() $61\times 61$, data type unit 16 and camera size of
$61\times 61$, data type unit 16 and camera size of ![]() $256\times 256$ pixels, run on a single thread of an Intel i5-10210U @ 4.2 GHz processor. Comparison of a simple implementation in Python, a just-in-time compiled optimization of the same code, using Numba, and a version written completely in C++ (compiled with GNU gcc-11).
$256\times 256$ pixels, run on a single thread of an Intel i5-10210U @ 4.2 GHz processor. Comparison of a simple implementation in Python, a just-in-time compiled optimization of the same code, using Numba, and a version written completely in C++ (compiled with GNU gcc-11).
The program was developed as a cross-platform application that can be run through a command-line-interface (CLI) or interactively through a graphical user interface (GUI) as shown in Figure 4. The core functionality of the algorithm is implemented in a single C++ class object. Visual interfaces interact with an instance of that class across threads through pointers, which allows live updates to be displayed immediately while maintaining a responsive interface without interrupting the reconstruction process. Furthermore, kernel settings for riCOM reconstruction and virtual STEM (vSTEM) settings, such as rotation angle due to Lorentz force, kernel size, filter, and the virtual detector size, can be changed during the process without interruption, which is helpful to find suitable settings interactively while spending the lowest amount of dose on the precious sample area.

Fig. 4. Layout of the GUI. The menu column on the left allows the user to change various settings, such as scan size, riCOM Kernel and filter settings, virtual STEM settings, and interfaces for live mode and file dialogues. During a running reconstruction, a CBED pattern is plotted at the bottom of this menu to visually assist interactive tuning of pattern center and integration area for vSTEM. All other windows are floating panels and can be moved and resized.
The riCOM base class is independent of specific camera models and data types, while additional dedicated classes provide live and file interfaces for given camera types/file formats. This allows for easy extendability of the program by simply including further interface classes. The current implementation includes a live and data interface for the MerlinEM as an example for frame-based data and a file-type interface for the event-based Timepix3 camera and is available on GitHub under a GPL license.
Experimental Details
The results presented in this paper are produced from data collected in two experiments. In the first experiment, a SrTiO3 focused ion beam (FIB) lamella is examined with a probe-corrected Thermo Fisher Titan![]() $^{3}$ (X-Ant-TEM) operated in a STEM mode. The resulting CBEDs are collected with a MerlinEM direct electron detector (Ballabriga et al., Reference Ballabriga, Campbell, Heijne, Llopart, Tlustos and Wong2011) and form 4D datasets for further analysis, as well as movies demonstrating the real-time processing power of the method. The experiment is performed with a beam energy of 300 keV and a convergence angle of 20 mrad.
$^{3}$ (X-Ant-TEM) operated in a STEM mode. The resulting CBEDs are collected with a MerlinEM direct electron detector (Ballabriga et al., Reference Ballabriga, Campbell, Heijne, Llopart, Tlustos and Wong2011) and form 4D datasets for further analysis, as well as movies demonstrating the real-time processing power of the method. The experiment is performed with a beam energy of 300 keV and a convergence angle of 20 mrad.
The second STEM experiment is performed on a silicalite-1 zeolite sample with a Thermo Fisher Themis Z (Advan-TEM). The data are collected with a custom-made Timepix3 detector (Poikela et al., Reference Poikela, Plosila, Westerlund, Campbell, De Gaspari, Llopart, Gromov, Kluit, Van Beuzekom, Zappon, Zappon and Zivkovic2014) based on an Advapix TP3 camera unit and is recorded in the event-based format. The beam energy and convergence angle used in the second experiment are 200 keV and 12 mrad, respectively.
All the datasets and movies recorded in both experiments, including necessary parameters for the reconstruction, can be found in the online repository (Yu & Friedrich, Reference Yu and Friedrich2021).
Results and Discussion
Real-Time Reconstruction
To demonstrate riCOM imaging, the software for real-time reconstruction is run directly on incoming data during live experiments. The computer receives frames of CBED patterns from the detector, and the software reads the data through a TCP socket. Throughout the process, the only extra prior knowledge to be provided to the algorithm is the COM of an undiffracted pattern in vacuum, so that the relative shift of COM at each probe position can be computed. Alternatively, it can also be approximated by averaging the COM from multiple probe positions, thereby omitting any calibration steps, making this method equivalent to more traditional imaging methods regarding the ease of use. This step also inherently corrects for systematic shifts of the CBED pattern away from the center of the detector. While scanning, some of the most basic parameters of the microscopic imaging system are tuned, for example, changing the defocus, astigmatism, and magnification, as shown in Figures 5a–5c. The live-updated results are recorded in Supplementary Movies.

Fig. 5. Real-time reconstruction of ![]() ${\rm SrTiO}_{\rm 3}$ while tuning the magnification, defocus, and stigmator. (a) The magnification is increased during the scanning. In the top most part, the contrast reveals a layered structure of the FIB lamella, and with increasing magnification the atoms can be captured in the image. (b) Tuning focus is reflected by the change of the shape of atomic columns. (c) Tuning the stigmator affects the electron probe sharpness and also the contrast between atom and vacuum. (d) Simultaneous imaging using riCOM, ADF, and iCOM. RiCOM successfully images the crystalline structure in the center of the image and the
${\rm SrTiO}_{\rm 3}$ while tuning the magnification, defocus, and stigmator. (a) The magnification is increased during the scanning. In the top most part, the contrast reveals a layered structure of the FIB lamella, and with increasing magnification the atoms can be captured in the image. (b) Tuning focus is reflected by the change of the shape of atomic columns. (c) Tuning the stigmator affects the electron probe sharpness and also the contrast between atom and vacuum. (d) Simultaneous imaging using riCOM, ADF, and iCOM. RiCOM successfully images the crystalline structure in the center of the image and the ![]() $\rm O$ columns, which is missing in the ADF image. The small kernel size used in the riCOM reconstruction reduces long-range intensity distribution shown in iCOM.
$\rm O$ columns, which is missing in the ADF image. The small kernel size used in the riCOM reconstruction reduces long-range intensity distribution shown in iCOM.
Defocus broadens the intensity distribution of the electron probe, and astigmatism has the effect of creating two focal points, making the beam to be first focused in one direction and then the other when traveling along the optical axis. This would reduce the electron beam sharpness and make the beam elliptical if out of focus, resulting in stretched atomic features in the images, as can be seen in Figure 5b in the region scanned before achieving the correct focus.
According to equation (3), the intensity in the iCOM image equals the cross-correlation between the projected electric potential of the material and the probe function, and therefore, the reduction in contrast as well as distortions of the atomic features in the riCOM reconstruction is directly related to these beam aberrations. Hence, users can tune optical conditions intuitively to maximize contrast and produce circular atoms with the live-updated results.
By changing the magnification during the scanning process, the step size is changed accordingly. The live process can still continue, although the intensity needs to be adjusted since ![]() $a$ is changed as the scan step size is changed, as shown in equation (4). Besides, the optimal kernel size changes with the magnification, as the spatial frequency of the desired features will be shifted when the step size is changed. However, since the kernel size can be adjusted during the process, a suitable choice can always be found by tuning the kernel size according to the quality of the live-updated reconstruction image.
$a$ is changed as the scan step size is changed, as shown in equation (4). Besides, the optimal kernel size changes with the magnification, as the spatial frequency of the desired features will be shifted when the step size is changed. However, since the kernel size can be adjusted during the process, a suitable choice can always be found by tuning the kernel size according to the quality of the live-updated reconstruction image.
In Figure 5d, a riCOM image rendered with a kernel size of 21 is compared with the annular dark field (ADF) image and the iCOM result. Apparent differences can be found in the center of the images, which appears to have a hole according to the ADF result but shows some crystalline structure in the riCOM and iCOM images, indicating possible extension of the crystalline material with lower thickness. ADF gives more significant contrast for differences in scattering ability, making it easier to distinguish ![]() ${\rm Sr}$ columns from
${\rm Sr}$ columns from ![]() ${\rm Ti} + {\rm O}$ columns, but also reduces the intensity of weak scatterers, such as thin regions and the pure
${\rm Ti} + {\rm O}$ columns, but also reduces the intensity of weak scatterers, such as thin regions and the pure ![]() ${\rm O}$ columns, to a level that is completely invisible, while riCOM and iCOM successfully image all three types of columns with a trade-off of less distinction between the columns. On the other hand, atomic structures are blurred by the long-range intensity variation in the iCOM result. The origin of this variation could be local strain, misorientation, contamination, charge accumulation, etc., but it is very difficult to pinpoint the actual cause. RiCOM with an appropriate kernel size suppresses these low-frequency signals and shows a clear image of atomic columns.
${\rm O}$ columns, to a level that is completely invisible, while riCOM and iCOM successfully image all three types of columns with a trade-off of less distinction between the columns. On the other hand, atomic structures are blurred by the long-range intensity variation in the iCOM result. The origin of this variation could be local strain, misorientation, contamination, charge accumulation, etc., but it is very difficult to pinpoint the actual cause. RiCOM with an appropriate kernel size suppresses these low-frequency signals and shows a clear image of atomic columns.
The examples shown in Figure 5 show how riCOM images can be used to fine tune optical systems in a similar manner as using ADF. Moreover, the method is superior to ADF imaging in terms of required electron dose and provides contrast also for the weak scatterers in the object, including thinner regions or atomic columns composed of lighter atoms. The high-pass characteristic of the suitable kernel size has shown to be helpful in highlighting features of higher spatial frequency and reduce low-frequency components, but it also means that the contrast interpretation has to be evaluated carefully, especially for quantitative analysis, as they can be affected by multiple factors unknowingly.
Comparison of Reconstruction Methods
In this section, results from the riCOM reconstruction are compared with other reconstruction methods that have the potential to provide real-time imaging. For 4D datasets, ADF images can be computed using a virtual detector which integrates all electrons in a specified region of the detector. The summing process is independent of the probe position and does not require information beyond the scope of a single diffraction pattern, thus making virtual ADF reconstruction possible for the real-time visualization of the dataset. To showcase the performance of riCOM reconstruction, it is compared with both ADF as a traditional imaging mode and SSB, which is generally considered as a highly dose efficient and quantitative ptychography method. For riCOM reconstruction, three results generated using different kernels are put into comparison, including two kernel sizes and one kernel incorporating a band-pass filter.
The dataset used for the comparison is a 4D dataset recorded from a silicalite-1 zeolite specimen. The dataset is recorded in a sparse array, in which the location where electrons hit the detector and the arrival time is recorded. This type of data format has several advantages over more commonly seen frame-by-frame types at suitable experiment conditions. For instance, in the case of low-dose imaging, sparse arrays result in datasets many times smaller than full-frame arrays, since only the pixels of the detector that successfully capture an electron generated data, while other inactive pixels remain silent. For riCOM reconstruction, this format also shows its strength in terms of processing speed. Yet another important feature of this format is that the arrival time can be used to adjust the dose in the post reconstruction stage. Since the arrival time of each electron is recorded, the amount of dose put into the reconstruction algorithm can be post-adjusted by reducing the acceptance time from each probe position. For example, with a dataset recorded with a beam dwell time of 6,000 ns, the dose for the post reconstruction can be reduced to one-third of the original dose if the acceptance time is set to be 2,000 ns since any electrons that arrive to the detector after the acceptance time for each probe position will be discarded.
Accordingly, five data treatment algorithms/setups are used for the experimental data at three different dose levels. The results are presented in Figure 6. Comparing the images generated by a virtual ADF detector with other reconstruction methods, it is obvious that even with the maximum dose, it is not enough to generate an interpretable ADF image. The vertical lines in the ADF image are a result of the camera being inactive for an unknown reason, which is discussed in previous work (Jannis et al., Reference Jannis, Hofer, Gao, Xie, Béché, Pennycook and Verbeeck2021). This, however, makes almost unnoticeable difference to other reconstruction methods, since the value of each pixel in the reconstructed image not only depends on the corresponding probe position but also on its surroundings. For SSB reconstruction, it includes a process to integrate specific regions in the CBED patterns according to their spatial frequency by performing Fourier transformation with respect to the probe position. Certain spatial frequencies are weighted more strongly from a larger integration area, thus creating a band-pass filtering effect (Yang et al., Reference Yang, Pennycook and Nellist2015; O'Leary et al., Reference O'Leary, Martinez, Liberti, Humphry, Kirkland and Nellist2021). The riCOM images of a smaller kernel size (riCOM-21) are shown to be similar to the SSB results, also manifested by the similarity of their frequency spectra, as low-frequency signal is suppressed. For the riCOM-61 result, by using a larger kernel size, more components at lower spatial frequencies can be found in the image. These components greatly increases the contrast for the long-range structure in the material, such as the pores and framework of the zeolite crystal, but reduces high-frequency components, making the short-range structures such as atomic columns less clear. This is especially highlighted in the result of 1/10 dose. However, by integrating a band-pass filter to the big kernel (riCOM-61-BP), noise from the high-frequency parts is removed and weights are redistributed to mid-range components from the low-frequency end. It results in a much clearer image of the atomic structure even at 1/10 dose. The filter used for the last column is designed to remove signals from 3.8 to 1.14 nm![]() $^{-1}$, with
$^{-1}$, with ![]() $k_{{\rm max}} = 60\ {\rm px}^{-1}$ and
$k_{{\rm max}} = 60\ {\rm px}^{-1}$ and ![]() $k_{{\rm min}} = 18\ {\rm px}^{-1}$.
$k_{{\rm min}} = 18\ {\rm px}^{-1}$.

Fig. 6. Reconstructed image from an experimental zeolite dataset with different doses (full dose: 1.27e+4e/Å![]() $^{2}$). ADF images are generated by integrating the intensities in the detector area beyond the convergence angle at each probe position. For SSB reconstruction, a frame-based dataset is first generated from the event array, with the detector space binned down to
$^{2}$). ADF images are generated by integrating the intensities in the detector area beyond the convergence angle at each probe position. For SSB reconstruction, a frame-based dataset is first generated from the event array, with the detector space binned down to ![]() $32\times 32$ (eight times smaller). For riCOM reconstruction, three different kernels are used: 21×21, 61×61, and 61×61 with a band-pass filter. The effect is, however, much less significant in other reconstruction methods. The insets show magnified versions of the center of their respective images, and the red arrows point out intensity fluctuations within the holes. The last row shows the Fourier transform of each reconstructed result. The radial averaged frequency spectra are represented with yellow curves, the frequency components of each kernel in red, and the line-integration approximation in a black dashed curve.
$32\times 32$ (eight times smaller). For riCOM reconstruction, three different kernels are used: 21×21, 61×61, and 61×61 with a band-pass filter. The effect is, however, much less significant in other reconstruction methods. The insets show magnified versions of the center of their respective images, and the red arrows point out intensity fluctuations within the holes. The last row shows the Fourier transform of each reconstructed result. The radial averaged frequency spectra are represented with yellow curves, the frequency components of each kernel in red, and the line-integration approximation in a black dashed curve.
In the third row, only ![]() $1/100$ of the electrons in the dataset is used for imaging. The insufficient number of electrons introduces a large amount of noise and hides the atomic structure in the images. Yet, for the reconstruction result of riCOM-61, the pores within the zeolite framework are preserved in the image. This is possibly due to the fact that features of a larger scale are reconstructed from more data points and is thus a result averaged over more possible integration paths. This kind of low-frequency components are only supported by kernels of larger size, explaining why other reconstruction methods shown here do not benefit from them and fail to present any meaningful information in the images.
$1/100$ of the electrons in the dataset is used for imaging. The insufficient number of electrons introduces a large amount of noise and hides the atomic structure in the images. Yet, for the reconstruction result of riCOM-61, the pores within the zeolite framework are preserved in the image. This is possibly due to the fact that features of a larger scale are reconstructed from more data points and is thus a result averaged over more possible integration paths. This kind of low-frequency components are only supported by kernels of larger size, explaining why other reconstruction methods shown here do not benefit from them and fail to present any meaningful information in the images.
Imaging of zeolites at atomic resolution with iDPC, a similar method as iCOM, has been demonstrated to be successful at low dose between 100 and 1,000 electrons/Å2 (Liu et al., Reference Liu, Wang, Zhu, Liu, Zhu, Guo, Alfilfil, Dong, Zhang and Han2020, Reference Liu, Liu, Wu, Zhou, Cheng, Lv, Cao, Zhang, Lin and Han2021). In a similar dose range, riCOM is capable of presenting structural features of the sample at different spatial frequencies, showing that the dose efficiency of the method is not sacrificed to enable real-time reconstruction.
While riCOM benefits from amplifying signals at specific frequencies so that clearer images of the lattice structures and atomic features can be captured, one has to bear in mind that the same effect is also applied to the statistical noise present in the experimental data. To study how noise affects the reconstructed images, one could compare results from ideal data with results from data with noise. However, for many reconstruction methods, it does not mean that the effect of noise can be simply acquired by subtracting one from the other since noise is not additive. Luckily, due to the linear independent nature, it is indeed the case for riCOM. In other words, the reconstructed image from a COM shift map with noise is exactly the same as the combination of the reconstructed image from a noise-free COM shift map and the one from pure noise. The latter is thus a suitable candidate for further noise analysis.
To demonstrate how noise is transferred to a reconstructed image at each frequency, a 4D dataset of a 20-nm-thick zeolite sample is simulated according to the condition used in the second experiment (see Experimental Details). The noise is separated from the dataset to reconstruct an ADF image of pure noise, and the noise-induced COM deviation is calculated by subtracting the COM shift map from the noise-included dataset from the one without noise. The COM deviation map is then used for riCOM reconstruction with a kernel size of 21 and 61. The reconstructed images of the ideal data and the noise are presented in the Supplementary Materials. The components at different radial frequencies of these images are plotted in Figure 7. Two major differences between ADF and riCOM images can be found. First, the noise amplitudes of ADF images are higher when the dose is higher, but the opposite for riCOM reconstruction is observed. It is due to the fact that the ADF intensity values follow a Poisson distribution, where the noise increases with the square root of the dose, while the signal scales linearly with the dose. The COM shift on the other hand is based on the spatial distribution of electrons, rather than the cumulative intensity, and thus is not directly linked to this kind of shot noise. However, the error of the COM estimation still decreases when more electrons are used. Therefore, despite different noise behaviors, the signal-to-noise ratios of both methods increase with dose. The second difference lies in the distribution of noise at different frequencies. For the ADF noise image, the noise is distributed equally at different frequencies, yet for riCOM, the noise is amplified according to the approximated weighting function based on the kernel size (equation (7)). Through this analysis, it is clear that not only the signal from the examined object but also the noise is affected by the weighting in frequency domain. This greatly changes how noise appears in the reconstructed images compared with traditional imaging methods, such as ADF, and is worthy of the attention of microscopists in order not to misinterpret features created by noise.

Fig. 7. Components of the noise images at different frequencies. The noise images are rendered by applying the virtual ADF detector, riCOM with kernel size 21, and riCOM with kernel size 61. Three levels of dose for noise realization are chosen, and the curves are drawn by averaging 30 random noise configurations at each dose. The weighting functions given by the line-integration approximation are also presented for the riCOM results in dashed lines. The reconstructed noise-free images, noise-included images, and the noise images can be found in the Supplementary Material.
The different reconstruction results in Figure 6 show a disagreement about the content inside of the pores that exist in the zeolite framework. Results from methods that give more weight to the high-frequency components, such as SSB and riCOM-21, show some intensity fluctuation inside of the pores, indicating the possible existence of dopants, yet these do not appear in the riCOM-61 image. In order to understand the cause of the difference, another simulation is run with the same condition to compare the reconstructed results with different kernel sizes in Figure 8. To eliminate the possibility that this difference originates from the presence of noise, the reconstruction is done without adding noise to the dataset. From each reconstructed image an intensity profile is drawn over the atom framework into the pore (Fig. 8a), which is indeed vacuum as designed for the simulation. The profile reveals that for riCOM-21, the intensity increases, while riCOM-61 shows a monotonic decay toward the center of the pore (Fig. 8b). The intensity increase for riCOM-21 cannot be explained by the projected atomic potential, since it can only decay when moving further away from the atoms.

Fig. 8. (a) Reconstruction results of a simulated zeolite dataset with different kernel sizes. The red and blue lines indicate the locations of intensity line profiles drawn in subplots (b). (b) The intensity profile shows that the intensity inside the hole area increases in riCOM-21 results but decays in riCOM-61 toward the center. (c) Step function for analogy shows that removing low frequency components may cause imaging artifacts similar to the ones seen in reconstruction results from smaller kernel sizes.
To investigate the origin of this false intensity, the Fourier transformed riCOM images are analyzed (Fig. 6). The bright spots at the lowest frequency correspond to the periodic structure of the pores and the framework. The intensity of these spots are greatly reduced in riCOM-21 but supported in riCOM-61, indicated by the approximated weighting function as red curves. This causes major differences to features that necessarily rely on such low-frequency signals. To illustrate the principle, we simplify the atom framework and the pore using a step function (Fig. 8c). By removing the low-frequency components, the step becomes a curve with a concave and a convex segment in the regions of the high and the low step, respectively. This step function analogy conceptually captures the differences between the zeolite framework and the holes and explains the protruding intensity in the hole for riCOM-21 as the effect of reduced low-frequency components. For riCOM-61, such components are included by the larger kernel size, so that no such phantom intensity can be found in the same area.
These examples show that the proposed method, like many other reconstruction methods, is capable of providing extra information compared with traditional imaging methods. RiCOM also shows great dose efficiency, allowing high-quality reconstruction results under low-dose conditions. The freedom to use different kernel sizes grants users the ability to tune the desired spatial frequency range, which is very important in order to avoid the misinterpretation of details in the image. Including more low-frequency components has shown to enable the reconstruction of long-range structures of the object with even lower amounts of electrons. This could be very useful for microscope operators when imaging objects of a larger scale.
Conclusion
In this paper, we propose and demonstrate a reconstruction method for real-time STEM based on the iCOM that is applicable to any kind of segmented detector dataset, including but not limited to 4D STEM. Through the derivation of the physical formulation, we illustrate the physical relevance and the benefits for numerically efficient implementations of this approach, motivating the application particularly in real-time imaging scenarios. The freedom to change the size of the kernel or incorporating filters are also discussed, with examples showing their effect.
It is shown that riCOM can effectively reproduce iCOM results but allows for more flexibility in terms of selecting contributing spatial frequencies. The method, including frequency band-pass filtering, depends only on the individual intensity distribution (or CBED pattern) at its corresponding real space location, which, in combination with a rather simple algorithm, creates a uniquely flexible and fast reconstruction method that requires very little user input. We further present a well optimized, interactive GUI implementation, developed in standard C++, and published open source on GitHub.
Demonstrations of the method on an operating microscope shows that firstly, the process is fast enough to keep up with the highest frame rate supported by currently available detectors, and secondly, providing a dynamic feedback to the microscope operator when tuning and optimizing the microscope parameters. This ability enables swift search of the sample, or region of interest, as well as adjustments of the imaging conditions, at potentially very low-dose conditions. The algorithm can run on any kind of data from which the COM of the electron diffraction pattern, or derivatives of COM such as DPC signals, can be calculated, and therefore, it is by no means limited to the hardware demonstrated in this paper.
Comparisons with results of other non-iterative reconstruction methods show that riCOM renders high-quality images on par with established methods, even at very low doses. The pros and cons of using different frequency components are discussed. Users can accordingly choose the most suitable designs of kernels and run simultaneously other imaging forming methods, in order to reach the highest dose efficiency or extract the most amount of knowledge from the investigated sample in real time.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S1431927622000617.
Acknowledgments
We acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 770887 PICOMETRICS) and funding from the European Union's Horizon 2020 research and innovation program under grant agreement No. 823717 ESTEEM3. This work was also supported by the FWO and FNRS within the 2Dto3D project of the EOS program (grant no. 30489208). J.V. and S.V.A. acknowledge funding from the University of Antwerp through a TOP BOF project. The direct electron detector (Merlin, Medipix3, Quantum Detectors) was funded by the Hercules fund from the Flemish Government. Further, the authors gratefully acknowledge Xiaobin Xie (Sichuan University, P. R. China) for providing the STO sample used in this study.