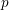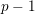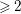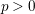Introduction
In this paper, we study dormant opers of rank
![]() $p-1$
over projective smooth curves of characteristic
$p-1$
over projective smooth curves of characteristic
![]() $p>0$
. In particular, we prove that the set of equivalence classes of dormant opers of rank
$p>0$
. In particular, we prove that the set of equivalence classes of dormant opers of rank
![]() $p-1$
over a curve of characteristic
$p-1$
over a curve of characteristic
![]() $p>0$
is of cardinality one.
$p>0$
is of cardinality one.
The notion of oper was introduced in [Reference Beilinson and Drinfeld1] (cf. also [Reference Beilinsion and Drinfeld2]). Let
![]() $k$
be an algebraically closed field, and let
$k$
be an algebraically closed field, and let
![]() $X$
be a projective smooth curve of genus
$X$
be a projective smooth curve of genus
![]() ${\geqslant}2$
over
${\geqslant}2$
over
![]() $k$
. Let us recall that an oper over
$k$
. Let us recall that an oper over
![]() $X/k$
is a suitable triple consisting of a locally free coherent
$X/k$
is a suitable triple consisting of a locally free coherent
![]() ${\mathcal{O}}_{X}$
-module, a connection on the module relative to
${\mathcal{O}}_{X}$
-module, a connection on the module relative to
![]() $X/k$
, and a filtration of the module. The study of opers in positive characteristic was initiated in, for instance, [Reference Joshi4, Reference Joshi and Pauly5, Reference Wakabayashi9, Reference Wakabayashi10]. Suppose that we are in the situation in which
$X/k$
, and a filtration of the module. The study of opers in positive characteristic was initiated in, for instance, [Reference Joshi4, Reference Joshi and Pauly5, Reference Wakabayashi9, Reference Wakabayashi10]. Suppose that we are in the situation in which
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p>0$
. Then, we shall say that a given oper is dormant if the
$p>0$
. Then, we shall say that a given oper is dormant if the
![]() $p$
-curvature of the connection of the oper is zero. We refer to Definition 1.1 (cf. also Definition 1.2) concerning the precise definition of the notion of “dormant oper” discussed in the present paper. It should be noted that a dormant oper of rank two is essentially the same as a dormant indigenous bundle studied in
$p$
-curvature of the connection of the oper is zero. We refer to Definition 1.1 (cf. also Definition 1.2) concerning the precise definition of the notion of “dormant oper” discussed in the present paper. It should be noted that a dormant oper of rank two is essentially the same as a dormant indigenous bundle studied in
![]() $p$
-adic Teichmüller theory (cf. [Reference Mochizuki7]).
$p$
-adic Teichmüller theory (cf. [Reference Mochizuki7]).
The main result of the present paper, which is a generalization of the first portion of [Reference Hoshi3], Theorem A (cf. Remark 2.1.1), is as follows (cf. Proposition 1.4, Theorem 2.1).
Theorem A. Let
![]() $k$
be an algebraically closed field of characteristic
$k$
be an algebraically closed field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $X$
be a projective smooth curve of genus
$X$
be a projective smooth curve of genus
![]() ${\geqslant}2$
over
${\geqslant}2$
over
![]() $k$
. Then, the set of equivalence classes of dormant opers of rank
$k$
. Then, the set of equivalence classes of dormant opers of rank
![]() $p-1$
over
$p-1$
over
![]() $X/k$
is of cardinality one.
$X/k$
is of cardinality one.
It should be noted that the fact that the set discussed in Theorem A is nonempty was already known (cf. Remark 1.4.2).
In [Reference Joshi4], Joshi posed a conjecture concerning the number of equivalence classes of dormant opers of rank
![]() $r$
over a projective smooth curve of genus
$r$
over a projective smooth curve of genus
![]() $g\geqslant 2$
over an algebraically closed field of characteristic
$g\geqslant 2$
over an algebraically closed field of characteristic
![]() $p>0$
for
$p>0$
for
![]() $p>C(r,g)\stackrel{\text{def}}{=}r(r-1)(r-2)(g-1)$
(cf. [Reference Joshi4, Conjecture 8.1]). Moreover, Wakabayashi proved this conjecture for a sufficiently general curve (cf. [Reference Wakabayashi10, Theorem 8.7.1]). It should be noted that the triple
$p>C(r,g)\stackrel{\text{def}}{=}r(r-1)(r-2)(g-1)$
(cf. [Reference Joshi4, Conjecture 8.1]). Moreover, Wakabayashi proved this conjecture for a sufficiently general curve (cf. [Reference Wakabayashi10, Theorem 8.7.1]). It should be noted that the triple
![]() $(r,g,p)\stackrel{\text{def}}{=}(p-1,g,p)$
(i.e., the triple in the case discussed in Theorem A) does not satisfy the condition
$(r,g,p)\stackrel{\text{def}}{=}(p-1,g,p)$
(i.e., the triple in the case discussed in Theorem A) does not satisfy the condition
![]() $p>C(r,g)$
unless
$p>C(r,g)$
unless
![]() $p\in \{2,3\}$
.
$p\in \{2,3\}$
.
1 Construction of dormant opers of rank
 $p-1$
$p-1$
In this section, let
![]() $p$
be a prime number, let
$p$
be a prime number, let
![]() $g\geqslant 2$
be an integer, let
$g\geqslant 2$
be an integer, let
![]() $k$
be an algebraically closed field of characteristic
$k$
be an algebraically closed field of characteristic
![]() $p$
, and let
$p$
, and let
![]() $X$
be a projective smooth curve over
$X$
be a projective smooth curve over
![]() $k$
(i.e., a scheme that is projective, smooth, geometrically connected, and of relative dimension one over
$k$
(i.e., a scheme that is projective, smooth, geometrically connected, and of relative dimension one over
![]() $k$
) of genus
$k$
) of genus
![]() $g$
. Write
$g$
. Write
![]() $X^{(1)}$
for the projective smooth curve over
$X^{(1)}$
for the projective smooth curve over
![]() $k$
obtained by base-changing
$k$
obtained by base-changing
![]() $X$
via the absolute Frobenius morphism of
$X$
via the absolute Frobenius morphism of
![]() $k$
,
$k$
,
![]() $F:X\rightarrow X^{(1)}$
for the relative Frobenius morphism over
$F:X\rightarrow X^{(1)}$
for the relative Frobenius morphism over
![]() $k$
,
$k$
,
![]() ${\mathcal{I}}\subseteq {\mathcal{O}}_{X\times _{k}X}$
for the ideal of
${\mathcal{I}}\subseteq {\mathcal{O}}_{X\times _{k}X}$
for the ideal of
![]() ${\mathcal{O}}_{X\times _{k}X}$
which defines the diagonal morphism with respect to
${\mathcal{O}}_{X\times _{k}X}$
which defines the diagonal morphism with respect to
![]() $X/k$
, and
$X/k$
, and
![]() $X_{(n)}\subseteq X\times _{k}X$
for the closed subscheme of
$X_{(n)}\subseteq X\times _{k}X$
for the closed subscheme of
![]() $X\times _{k}X$
defined by the ideal
$X\times _{k}X$
defined by the ideal
![]() ${\mathcal{I}}^{n+1}\subseteq {\mathcal{O}}_{X\times _{k}X}$
(where
${\mathcal{I}}^{n+1}\subseteq {\mathcal{O}}_{X\times _{k}X}$
(where
![]() $n$
is a nonnegative integer). In particular, it follows that
$n$
is a nonnegative integer). In particular, it follows that
![]() ${\mathcal{I}}/{\mathcal{I}}^{2}=\unicode[STIX]{x1D714}_{X/k}$
(resp.,
${\mathcal{I}}/{\mathcal{I}}^{2}=\unicode[STIX]{x1D714}_{X/k}$
(resp.,
![]() ${\mathcal{H}}om_{{\mathcal{O}}_{X}}({\mathcal{I}}/{\mathcal{I}}^{2},{\mathcal{O}}_{X})=\unicode[STIX]{x1D70F}_{X/k}$
), where we use the notation
${\mathcal{H}}om_{{\mathcal{O}}_{X}}({\mathcal{I}}/{\mathcal{I}}^{2},{\mathcal{O}}_{X})=\unicode[STIX]{x1D70F}_{X/k}$
), where we use the notation
![]() $\unicode[STIX]{x1D714}$
(resp.,
$\unicode[STIX]{x1D714}$
(resp.,
![]() $\unicode[STIX]{x1D70F}$
) to denote the cotangent (resp., tangent) sheaf. Finally, write
$\unicode[STIX]{x1D70F}$
) to denote the cotangent (resp., tangent) sheaf. Finally, write
![]() $d:{\mathcal{O}}_{X}\rightarrow \unicode[STIX]{x1D714}_{X/k}$
for the exterior differentiation operator.
$d:{\mathcal{O}}_{X}\rightarrow \unicode[STIX]{x1D714}_{X/k}$
for the exterior differentiation operator.
Let us define the notion of dormant oper, as well as the notion of equivalence of dormant opers, discussed in the present paper as follows (cf., e.g., [Reference Joshi4, §3]; also [Reference Joshi and Pauly5, Definitions 3.1.1, 3.1.2 and (1)–(5) of pp. 51–52]).
Definition 1.1. Let
![]() $r$
be a positive integer. Then, we shall say that a collection of data
$r$
be a positive integer. Then, we shall say that a collection of data
consisting of a locally free coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{E}}$
, a connection
${\mathcal{E}}$
, a connection
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
on
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
on
![]() ${\mathcal{E}}$
relative to
${\mathcal{E}}$
relative to
![]() $X/k$
, and a filtration
$X/k$
, and a filtration
![]() $\{0\}={\mathcal{E}}_{r}\subseteq {\mathcal{E}}_{r-1}\subseteq \cdots \subseteq {\mathcal{E}}_{1}\subseteq {\mathcal{E}}_{0}={\mathcal{E}}$
by
$\{0\}={\mathcal{E}}_{r}\subseteq {\mathcal{E}}_{r-1}\subseteq \cdots \subseteq {\mathcal{E}}_{1}\subseteq {\mathcal{E}}_{0}={\mathcal{E}}$
by
![]() ${\mathcal{O}}_{X}$
-submodules of
${\mathcal{O}}_{X}$
-submodules of
![]() ${\mathcal{E}}$
is a dormant oper of rank
${\mathcal{E}}$
is a dormant oper of rank
![]() $r$
over
$r$
over
![]() $X/k$
if the following five conditions are satisfied.
$X/k$
if the following five conditions are satisfied.
(1) For every
 $i\in \{1,\ldots ,r\}$
, the subquotient
$i\in \{1,\ldots ,r\}$
, the subquotient
 ${\mathcal{E}}_{i-1}/{\mathcal{E}}_{i}$
is an invertible sheaf on
${\mathcal{E}}_{i-1}/{\mathcal{E}}_{i}$
is an invertible sheaf on
 $X$
.
$X$
.(2) For every
 $i\in \{1,\ldots ,r\}$
, it holds that
$i\in \{1,\ldots ,r\}$
, it holds that
 $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}({\mathcal{E}}_{i})\subseteq {\mathcal{E}}_{i-1}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
.
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}({\mathcal{E}}_{i})\subseteq {\mathcal{E}}_{i-1}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
.(3) For every
 $i\in \{1,\ldots ,r-1\}$
, the homomorphism of
$i\in \{1,\ldots ,r-1\}$
, the homomorphism of
 ${\mathcal{O}}_{X}$
-modules obtained by forming the composite (cf.
${\mathcal{O}}_{X}$
-modules obtained by forming the composite (cf. $$\begin{eqnarray}{\mathcal{E}}_{i}~\stackrel{\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}}{\rightarrow }~{\mathcal{E}}_{i-1}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}~{\twoheadrightarrow}~({\mathcal{E}}_{i-1}/{\mathcal{E}}_{i})\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}~\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{i}~\stackrel{\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}}{\rightarrow }~{\mathcal{E}}_{i-1}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}~{\twoheadrightarrow}~({\mathcal{E}}_{i-1}/{\mathcal{E}}_{i})\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}~\end{eqnarray}$$
 $(2)$
) determines an isomorphism
$(2)$
) determines an isomorphism
 ${\mathcal{E}}_{i}/{\mathcal{E}}_{i+1}\stackrel{{\sim}}{\rightarrow }({\mathcal{E}}_{i-1}/{\mathcal{E}}_{i})\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
of invertible sheaves on
${\mathcal{E}}_{i}/{\mathcal{E}}_{i+1}\stackrel{{\sim}}{\rightarrow }({\mathcal{E}}_{i-1}/{\mathcal{E}}_{i})\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
of invertible sheaves on
 $X$
(cf.
$X$
(cf.
 $(1)$
).
$(1)$
).(4) The
 $p$
-curvature of
$p$
-curvature of
 $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
is zero.
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
is zero.(5) There exists an isomorphism
 $(\det {\mathcal{E}},\det \unicode[STIX]{x1D6FB}_{{\mathcal{E}}})\stackrel{{\sim}}{\rightarrow }({\mathcal{O}}_{X},d)$
.
$(\det {\mathcal{E}},\det \unicode[STIX]{x1D6FB}_{{\mathcal{E}}})\stackrel{{\sim}}{\rightarrow }({\mathcal{O}}_{X},d)$
.
Definition 1.2. Let
![]() $r$
be a positive integer, and let
$r$
be a positive integer, and let
 $$\begin{eqnarray}\displaystyle \mathfrak{E}~\stackrel{\text{def}}{=}~({\mathcal{E}},\,\unicode[STIX]{x1D6FB}_{{\mathcal{E}}},\,\{0\}={\mathcal{E}}_{r}\subseteq {\mathcal{E}}_{r-1}\subseteq \cdots \subseteq {\mathcal{E}}_{1}\subseteq {\mathcal{E}}_{0}={\mathcal{E}}), & & \displaystyle \nonumber\\ \displaystyle \mathfrak{F}~\stackrel{\text{def}}{=}~({\mathcal{F}},\,\unicode[STIX]{x1D6FB}_{{\mathcal{F}}},\,\{0\}={\mathcal{F}}_{r}\subseteq {\mathcal{F}}_{r-1}\subseteq \cdots \subseteq {\mathcal{F}}_{1}\subseteq {\mathcal{F}}_{0}={\mathcal{F}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{E}~\stackrel{\text{def}}{=}~({\mathcal{E}},\,\unicode[STIX]{x1D6FB}_{{\mathcal{E}}},\,\{0\}={\mathcal{E}}_{r}\subseteq {\mathcal{E}}_{r-1}\subseteq \cdots \subseteq {\mathcal{E}}_{1}\subseteq {\mathcal{E}}_{0}={\mathcal{E}}), & & \displaystyle \nonumber\\ \displaystyle \mathfrak{F}~\stackrel{\text{def}}{=}~({\mathcal{F}},\,\unicode[STIX]{x1D6FB}_{{\mathcal{F}}},\,\{0\}={\mathcal{F}}_{r}\subseteq {\mathcal{F}}_{r-1}\subseteq \cdots \subseteq {\mathcal{F}}_{1}\subseteq {\mathcal{F}}_{0}={\mathcal{F}}) & & \displaystyle \nonumber\end{eqnarray}$$
be dormant opers of rank
![]() $r$
over
$r$
over
![]() $X/k$
. Then, we shall say that
$X/k$
. Then, we shall say that
![]() $\mathfrak{E}$
is equivalent to
$\mathfrak{E}$
is equivalent to
![]() $\mathfrak{F}$
if the following condition is satisfied. There exists a triple
$\mathfrak{F}$
if the following condition is satisfied. There exists a triple
![]() $({\mathcal{L}},\unicode[STIX]{x1D6FB}_{{\mathcal{L}}},\unicode[STIX]{x1D719})$
consisting of an invertible sheaf
$({\mathcal{L}},\unicode[STIX]{x1D6FB}_{{\mathcal{L}}},\unicode[STIX]{x1D719})$
consisting of an invertible sheaf
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $X$
, a connection
$X$
, a connection
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{L}}}$
on
$\unicode[STIX]{x1D6FB}_{{\mathcal{L}}}$
on
![]() ${\mathcal{L}}$
relative to
${\mathcal{L}}$
relative to
![]() $X/k$
, and a horizontal isomorphism
$X/k$
, and a horizontal isomorphism
![]() $\unicode[STIX]{x1D719}$
of
$\unicode[STIX]{x1D719}$
of
![]() $({\mathcal{E}},\unicode[STIX]{x1D6FB}_{{\mathcal{E}}})$
with
$({\mathcal{E}},\unicode[STIX]{x1D6FB}_{{\mathcal{E}}})$
with
![]() $({\mathcal{F}},\unicode[STIX]{x1D6FB}_{{\mathcal{F}}})\otimes _{{\mathcal{O}}_{X}}({\mathcal{L}},\unicode[STIX]{x1D6FB}_{{\mathcal{L}}})$
such that
$({\mathcal{F}},\unicode[STIX]{x1D6FB}_{{\mathcal{F}}})\otimes _{{\mathcal{O}}_{X}}({\mathcal{L}},\unicode[STIX]{x1D6FB}_{{\mathcal{L}}})$
such that
![]() $\unicode[STIX]{x1D719}$
maps, for each
$\unicode[STIX]{x1D719}$
maps, for each
![]() $i\in \{0,\ldots ,r\}$
, the subsheaf
$i\in \{0,\ldots ,r\}$
, the subsheaf
![]() ${\mathcal{E}}_{i}\subseteq {\mathcal{E}}$
isomorphically onto the subsheaf
${\mathcal{E}}_{i}\subseteq {\mathcal{E}}$
isomorphically onto the subsheaf
![]() ${\mathcal{F}}_{i}\otimes _{{\mathcal{O}}_{X}}{\mathcal{L}}\subseteq {\mathcal{F}}\otimes _{{\mathcal{O}}_{X}}{\mathcal{L}}$
.
${\mathcal{F}}_{i}\otimes _{{\mathcal{O}}_{X}}{\mathcal{L}}\subseteq {\mathcal{F}}\otimes _{{\mathcal{O}}_{X}}{\mathcal{L}}$
.
Remark 1.2.1. It should be noted that the notion of the “equivalence class of a dormant oper of rank
![]() $r$
” of the present paper coincides with the notion of the “isomorphism class of a dormant
$r$
” of the present paper coincides with the notion of the “isomorphism class of a dormant
![]() $\text{PGL}(r)$
-oper” in the terminology given in [Reference Joshi4, §3].
$\text{PGL}(r)$
-oper” in the terminology given in [Reference Joshi4, §3].
Remark 1.2.2. It follows immediately from the various definitions involved that the notion of dormant oper of rank two is essentially the same as the notion of dormant indigenous bundle studied in [Reference Mochizuki7].
In the remainder of the present section, let us construct a dormant oper of rank
![]() $p-1$
over
$p-1$
over
![]() $X/k$
. We shall write
$X/k$
. We shall write
for the
![]() ${\mathcal{O}}_{X^{(1)}}$
-module obtained by forming the cokernel of the natural homomorphism
${\mathcal{O}}_{X^{(1)}}$
-module obtained by forming the cokernel of the natural homomorphism
![]() ${\mathcal{O}}_{X^{(1)}}\rightarrow F_{\ast }{\mathcal{O}}_{X}$
. It should be noted that since
${\mathcal{O}}_{X^{(1)}}\rightarrow F_{\ast }{\mathcal{O}}_{X}$
. It should be noted that since
![]() $F$
is finite flat of degree
$F$
is finite flat of degree
![]() $p$
, the
$p$
, the
![]() ${\mathcal{O}}_{X^{(1)}}$
-module
${\mathcal{O}}_{X^{(1)}}$
-module
![]() $B_{1}$
, and hence also the
$B_{1}$
, and hence also the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() $F^{\ast }B_{1}$
, is locally free of rank
$F^{\ast }B_{1}$
, is locally free of rank
![]() $p-1$
.
$p-1$
.
Lemma 1.3. The following hold.
(i) The natural homomorphism
 ${\mathcal{O}}_{X^{(1)}}\rightarrow F_{\ast }{\mathcal{O}}_{X}$
and the homomorphism
${\mathcal{O}}_{X^{(1)}}\rightarrow F_{\ast }{\mathcal{O}}_{X}$
and the homomorphism
 $F^{\ast }F_{\ast }{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}$
determined by multiplication of the ring
$F^{\ast }F_{\ast }{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}$
determined by multiplication of the ring
 ${\mathcal{O}}_{X}$
determine an isomorphism of
${\mathcal{O}}_{X}$
determine an isomorphism of
 ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules  $$\begin{eqnarray}F^{\ast }F_{\ast }{\mathcal{O}}_{X}~\stackrel{{\sim}}{\longrightarrow }~{\mathcal{O}}_{X}\oplus F^{\ast }B_{1}.\end{eqnarray}$$
$$\begin{eqnarray}F^{\ast }F_{\ast }{\mathcal{O}}_{X}~\stackrel{{\sim}}{\longrightarrow }~{\mathcal{O}}_{X}\oplus F^{\ast }B_{1}.\end{eqnarray}$$
(ii) The natural morphism
 $X\times _{X^{(1)}}X\rightarrow X\times _{k}X$
over
$X\times _{X^{(1)}}X\rightarrow X\times _{k}X$
over
 $k$
determines an isomorphism over
$k$
determines an isomorphism over
 $k$
$k$
 $$\begin{eqnarray}X\times _{X^{(1)}}X~\stackrel{{\sim}}{\longrightarrow }~X_{(p-1)}.\end{eqnarray}$$
$$\begin{eqnarray}X\times _{X^{(1)}}X~\stackrel{{\sim}}{\longrightarrow }~X_{(p-1)}.\end{eqnarray}$$
(iii) The closed immersion
 $X_{(1)}{\hookrightarrow}X\times _{k}X$
factors through the closed subscheme
$X_{(1)}{\hookrightarrow}X\times _{k}X$
factors through the closed subscheme
 $X\times _{X^{(1)}}X\subseteq X\times _{k}X$
:
$X\times _{X^{(1)}}X\subseteq X\times _{k}X$
:  $$\begin{eqnarray}X_{(1)}~{\hookrightarrow}~X\times _{X^{(1)}}X~{\hookrightarrow}~X\times _{k}X.\end{eqnarray}$$
$$\begin{eqnarray}X_{(1)}~{\hookrightarrow}~X\times _{X^{(1)}}X~{\hookrightarrow}~X\times _{k}X.\end{eqnarray}$$
(iv) The isomorphism
 $X\times _{X^{(1)}}X\stackrel{{\sim}}{\rightarrow }X_{(p-1)}$
of
$X\times _{X^{(1)}}X\stackrel{{\sim}}{\rightarrow }X_{(p-1)}$
of
 $(\text{ii})$
, together with the Cartesian diagramdetermines isomorphisms of
$(\text{ii})$
, together with the Cartesian diagramdetermines isomorphisms of
 ${\mathcal{O}}_{X}$
-modules which are compatible with the respective natural surjections onto
${\mathcal{O}}_{X}$
-modules which are compatible with the respective natural surjections onto $$\begin{eqnarray}F^{\ast }F_{\ast }{\mathcal{O}}_{X}~\stackrel{{\sim}}{\longrightarrow }~\text{pr}_{1\ast }{\mathcal{O}}_{X\times _{X^{(1)}}X}~\stackrel{{\sim}}{\longleftarrow }~\text{pr}_{1\ast }{\mathcal{O}}_{X_{(p-1)}},\end{eqnarray}$$
$$\begin{eqnarray}F^{\ast }F_{\ast }{\mathcal{O}}_{X}~\stackrel{{\sim}}{\longrightarrow }~\text{pr}_{1\ast }{\mathcal{O}}_{X\times _{X^{(1)}}X}~\stackrel{{\sim}}{\longleftarrow }~\text{pr}_{1\ast }{\mathcal{O}}_{X_{(p-1)}},\end{eqnarray}$$
 ${\mathcal{O}}_{X}$
(arising from the diagonal morphism with respect to
${\mathcal{O}}_{X}$
(arising from the diagonal morphism with respect to
 $X/X^{(1)}$
) from each of these three modules.
$X/X^{(1)}$
) from each of these three modules.(v) The isomorphisms
 $F^{\ast }F_{\ast }{\mathcal{O}}_{X}\stackrel{{\sim}}{\rightarrow }\text{pr}_{1\ast }{\mathcal{O}}_{X\times _{X^{(1)}}X}\stackrel{{\sim}}{\leftarrow }\text{pr}_{1\ast }{\mathcal{O}}_{X_{(p-1)}}$
of
$F^{\ast }F_{\ast }{\mathcal{O}}_{X}\stackrel{{\sim}}{\rightarrow }\text{pr}_{1\ast }{\mathcal{O}}_{X\times _{X^{(1)}}X}\stackrel{{\sim}}{\leftarrow }\text{pr}_{1\ast }{\mathcal{O}}_{X_{(p-1)}}$
of
 $(\text{iv})$
restrict, relative to the isomorphism
$(\text{iv})$
restrict, relative to the isomorphism
 $F^{\ast }F_{\ast }{\mathcal{O}}_{X}\stackrel{{\sim}}{\rightarrow }{\mathcal{O}}_{X}\oplus F^{\ast }B_{1}$
of
$F^{\ast }F_{\ast }{\mathcal{O}}_{X}\stackrel{{\sim}}{\rightarrow }{\mathcal{O}}_{X}\oplus F^{\ast }B_{1}$
of
 $(\text{i})$
, to isomorphisms of
$(\text{i})$
, to isomorphisms of
 ${\mathcal{O}}_{X}$
-submodules
${\mathcal{O}}_{X}$
-submodules  $$\begin{eqnarray}\displaystyle F^{\ast }B_{1}~\stackrel{{\sim}}{\longrightarrow }~\text{Ker}(\text{pr}_{1\ast }{\mathcal{O}}_{X\times _{X^{(1)}}X}~{\twoheadrightarrow}~{\mathcal{O}}_{X})~\stackrel{{\sim}}{\longleftarrow }~\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F^{\ast }B_{1}~\stackrel{{\sim}}{\longrightarrow }~\text{Ker}(\text{pr}_{1\ast }{\mathcal{O}}_{X\times _{X^{(1)}}X}~{\twoheadrightarrow}~{\mathcal{O}}_{X})~\stackrel{{\sim}}{\longleftarrow }~\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p}). & & \displaystyle \nonumber\end{eqnarray}$$
(vi) The
 ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
 $\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p})$
admits a filtration
$\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p})$
admits a filtration  $$\begin{eqnarray}\displaystyle \{0\} & = & \displaystyle \text{pr}_{1\ast }({\mathcal{I}}^{p}/{\mathcal{I}}^{p})~\subseteq ~\text{pr}_{1\ast }({\mathcal{I}}^{p-1}/{\mathcal{I}}^{p})~\subseteq ~\cdots ~\subseteq ~\text{pr}_{1\ast }({\mathcal{I}}^{2}/{\mathcal{I}}^{p})\nonumber\\ \displaystyle & & \displaystyle \subseteq ~\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{0\} & = & \displaystyle \text{pr}_{1\ast }({\mathcal{I}}^{p}/{\mathcal{I}}^{p})~\subseteq ~\text{pr}_{1\ast }({\mathcal{I}}^{p-1}/{\mathcal{I}}^{p})~\subseteq ~\cdots ~\subseteq ~\text{pr}_{1\ast }({\mathcal{I}}^{2}/{\mathcal{I}}^{p})\nonumber\\ \displaystyle & & \displaystyle \subseteq ~\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p}).\nonumber\end{eqnarray}$$
(vii) The
 ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
 $F^{\ast }\det B_{1}=\det (F^{\ast }B_{1})$
is isomorphic to
$F^{\ast }\det B_{1}=\det (F^{\ast }B_{1})$
is isomorphic to
 $\unicode[STIX]{x1D714}_{X/k}^{\otimes p(p-1)/2}$
.
$\unicode[STIX]{x1D714}_{X/k}^{\otimes p(p-1)/2}$
.(viii) It holds that
 $\deg B_{1}=(p-1)(g-1)$
.
$\deg B_{1}=(p-1)(g-1)$
.(ix) There exists an invertible sheaf
 ${\mathcal{L}}^{\circ }$
on
${\mathcal{L}}^{\circ }$
on
 $X^{(1)}$
such that
$X^{(1)}$
such that
 $\det ({\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}B_{1})$
$\det ({\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}B_{1})$
 $(=({\mathcal{L}}^{\circ })^{\otimes p-1}\otimes _{{\mathcal{O}}_{X^{(1)}}}\det B_{1})$
is isomorphic to
$(=({\mathcal{L}}^{\circ })^{\otimes p-1}\otimes _{{\mathcal{O}}_{X^{(1)}}}\det B_{1})$
is isomorphic to
 ${\mathcal{O}}_{X^{(1)}}$
.
${\mathcal{O}}_{X^{(1)}}$
.
Proof. Assertions (i) and (ii) follow immediately from local explicit calculations. Assertions (iii) and (iv) follow from assertion (ii). Assertion (v) follows from assertion (iv). Assertion (vi) is immediate. Assertion (vii) follows from assertion (vi). Assertion (viii) follows from assertion (vii). Assertion (ix) follows from assertion (viii). This completes the proof of Lemma 1.3. ◻
Let
![]() ${\mathcal{L}}^{\circ }$
be as in Lemma 1.3(ix) (cf. Remark 1.4.1 below). We shall write
${\mathcal{L}}^{\circ }$
be as in Lemma 1.3(ix) (cf. Remark 1.4.1 below). We shall write
Then, it follows immediately from the definition of a connection that the factorization of Lemma 1.3(iii) determines a connection on the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{E}}^{\circ }$
relative to
${\mathcal{E}}^{\circ }$
relative to
![]() $X/k$
. We shall write
$X/k$
. We shall write
for this connection on
![]() ${\mathcal{E}}^{\circ }$
. Moreover, the isomorphism
${\mathcal{E}}^{\circ }$
. Moreover, the isomorphism
![]() $F^{\ast }B_{1}\stackrel{{\sim}}{\rightarrow }\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p})$
of Lemma 1.3(v) and the filtration of
$F^{\ast }B_{1}\stackrel{{\sim}}{\rightarrow }\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p})$
of Lemma 1.3(v) and the filtration of
![]() $\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p})$
of Lemma 1.3(vi) determine a filtration of
$\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{p})$
of Lemma 1.3(vi) determine a filtration of
![]() ${\mathcal{E}}^{\circ }$
${\mathcal{E}}^{\circ }$
(Thus, it follows immediately from the definition of the filtration that
![]() ${\mathcal{E}}^{\circ }/{\mathcal{E}}_{1}^{\circ }\cong F^{\ast }{\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X}}\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{2})=F^{\ast }{\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
.)
${\mathcal{E}}^{\circ }/{\mathcal{E}}_{1}^{\circ }\cong F^{\ast }{\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X}}\text{pr}_{1\ast }({\mathcal{I}}/{\mathcal{I}}^{2})=F^{\ast }{\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
.)
Proposition 1.4. The collection of data
forms a dormant oper of rank
![]() $p-1$
over
$p-1$
over
![]() $X/k$
.
$X/k$
.
Proof. The assertion that
![]() $\mathfrak{E}^{\circ }$
satisfies condition (1) of Definition 1.1 follows from the definition of the
$\mathfrak{E}^{\circ }$
satisfies condition (1) of Definition 1.1 follows from the definition of the
![]() ${\mathcal{O}}_{X}$
-submodules
${\mathcal{O}}_{X}$
-submodules
![]() ${\mathcal{E}}_{i}^{\circ }\subseteq {\mathcal{E}}^{\circ }$
. The assertion that
${\mathcal{E}}_{i}^{\circ }\subseteq {\mathcal{E}}^{\circ }$
. The assertion that
![]() $\mathfrak{E}^{\circ }$
satisfies conditions (2) and (3) of Definition 1.1 follows immediately from a local explicit calculation (cf. also [Reference Joshi and Pauly5, Theorem 3.1.6]). The assertion that
$\mathfrak{E}^{\circ }$
satisfies conditions (2) and (3) of Definition 1.1 follows immediately from a local explicit calculation (cf. also [Reference Joshi and Pauly5, Theorem 3.1.6]). The assertion that
![]() $\mathfrak{E}^{\circ }$
satisfies condition (4) of Definition 1.1 follows from the definition of the connection
$\mathfrak{E}^{\circ }$
satisfies condition (4) of Definition 1.1 follows from the definition of the connection
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
. The assertion that
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
. The assertion that
![]() $\mathfrak{E}^{\circ }$
satisfies condition (5) of Definition 1.1 follows from the fact that
$\mathfrak{E}^{\circ }$
satisfies condition (5) of Definition 1.1 follows from the fact that
![]() $\det ({\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}B_{1})$
is isomorphic to
$\det ({\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}B_{1})$
is isomorphic to
![]() ${\mathcal{O}}_{X^{(1)}}$
(cf. Lemma 1.3(ix)), together with the definition of the connection
${\mathcal{O}}_{X^{(1)}}$
(cf. Lemma 1.3(ix)), together with the definition of the connection
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
. This completes the proof of Proposition 1.4.◻
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
. This completes the proof of Proposition 1.4.◻
Remark 1.4.1. Let us observe that the choice of
![]() ${\mathcal{L}}^{\circ }$
as in Lemma 1.3(ix) is not unique. More precisely, if we write
${\mathcal{L}}^{\circ }$
as in Lemma 1.3(ix) is not unique. More precisely, if we write
![]() $(\text{Pic}\,X)[p-1]\subseteq \text{Pic}\,X$
for the subgroup of
$(\text{Pic}\,X)[p-1]\subseteq \text{Pic}\,X$
for the subgroup of
![]() $\text{Pic}\,X$
obtained by forming the kernel of the endomorphism of
$\text{Pic}\,X$
obtained by forming the kernel of the endomorphism of
![]() $\text{Pic}\,X$
given by multiplication by
$\text{Pic}\,X$
given by multiplication by
![]() $p-1$
, then the set consisting of isomorphism classes of possible
$p-1$
, then the set consisting of isomorphism classes of possible
![]() ${\mathcal{L}}^{\circ }$
s forms a
${\mathcal{L}}^{\circ }$
s forms a
![]() $(\text{Pic}\,X)[p-1]$
-torsor. On the other hand, it is immediate from the various definitions involved that the adoption of another possible
$(\text{Pic}\,X)[p-1]$
-torsor. On the other hand, it is immediate from the various definitions involved that the adoption of another possible
![]() ${\mathcal{L}}^{\circ }$
does not affect the equivalence class of the dormant oper of Proposition 1.4.
${\mathcal{L}}^{\circ }$
does not affect the equivalence class of the dormant oper of Proposition 1.4.
Remark 1.4.2. It should be noted that the assertion that every
![]() $X/k$
admits a dormant oper of rank
$X/k$
admits a dormant oper of rank
![]() $p-1$
was already essentially proved. For instance, it follows immediately, in light of Remark 1.2.2, from [Reference Mochizuki7, Chapter II, Theorem 2.8] (cf. also the final Remark of [Reference Mochizuki7, Chapter IV, §2.1]), that every
$p-1$
was already essentially proved. For instance, it follows immediately, in light of Remark 1.2.2, from [Reference Mochizuki7, Chapter II, Theorem 2.8] (cf. also the final Remark of [Reference Mochizuki7, Chapter IV, §2.1]), that every
![]() $X/k$
admits a dormant oper of rank two; thus, by considering the
$X/k$
admits a dormant oper of rank two; thus, by considering the
![]() $(p-2)$
-nd symmetric power of a dormant oper of rank two (cf. also the discussion concerning
$(p-2)$
-nd symmetric power of a dormant oper of rank two (cf. also the discussion concerning
![]() ${\mathcal{G}}_{r}(\unicode[STIX]{x1D703})$
in [Reference Joshi and Pauly5, §3.2]), we conclude that every
${\mathcal{G}}_{r}(\unicode[STIX]{x1D703})$
in [Reference Joshi and Pauly5, §3.2]), we conclude that every
![]() $X/k$
admits a dormant oper of rank
$X/k$
admits a dormant oper of rank
![]() $p-1$
.
$p-1$
.
2 Uniqueness of dormant opers of rank
 $p-1$
$p-1$
In this section, we maintain the notation of §1. In particular, we have a projective smooth curve
![]() $X$
over
$X$
over
![]() $k$
. In this section, we prove the following theorem.
$k$
. In this section, we prove the following theorem.
Theorem 2.1. Every dormant oper of rank
![]() $p-1$
over
$p-1$
over
![]() $X/k$
is equivalent (cf. Definition 1.2) to the dormant oper of Proposition 1.4 (cf. also Remark 1.4.1).
$X/k$
is equivalent (cf. Definition 1.2) to the dormant oper of Proposition 1.4 (cf. also Remark 1.4.1).
Remark 2.1.1. Theorem 2.1 is a generalization of the first portion of [Reference Hoshi3], Theorem A.
Remark 2.1.2. As discussed in Remark 1.2.1, the notion of “dormant oper of rank
![]() $r$
” of the present paper is essentially the same as the notion of “dormant
$r$
” of the present paper is essentially the same as the notion of “dormant
![]() $\text{PGL}(r)$
-oper” in the terminology given in [Reference Joshi4, §3]. On the other hand, one may find the definition of the notion of
$\text{PGL}(r)$
-oper” in the terminology given in [Reference Joshi4, §3]. On the other hand, one may find the definition of the notion of
![]() $G$
-oper in, for instance, [Reference Beilinson and Drinfeld1, §3], [Reference Beilinsion and Drinfeld2, §1], for a more general algebraic group
$G$
-oper in, for instance, [Reference Beilinson and Drinfeld1, §3], [Reference Beilinsion and Drinfeld2, §1], for a more general algebraic group
![]() $G$
. Thus, by imposing a condition similar to condition (4) of Definition 1.1 on such a
$G$
. Thus, by imposing a condition similar to condition (4) of Definition 1.1 on such a
![]() $G$
-oper, one may define the notion of dormant
$G$
-oper, one may define the notion of dormant
![]() $G$
-oper (as well as the notion of the isomorphism class of a dormant
$G$
-oper (as well as the notion of the isomorphism class of a dormant
![]() $G$
-oper).
$G$
-oper).
It should be noted that the proof of Theorem 2.1, that is, the proof of the main result of the present paper, may give a proof of the assertion that the set of isomorphism classes of dormant
![]() $G$
-opers over
$G$
-opers over
![]() $X/k$
is of cardinality one for a suitable algebraic group
$X/k$
is of cardinality one for a suitable algebraic group
![]() $G$
. We leave the routine details of such generalizations to the interested reader.
$G$
. We leave the routine details of such generalizations to the interested reader.
To complete the verification of Theorem 2.1, let
be a dormant oper of rank
![]() $p-1$
over
$p-1$
over
![]() $X/k$
. We shall write
$X/k$
. We shall write
Then, it follows from the definition of a dormant oper that both
![]() $(\unicode[STIX]{x1D6EF}^{\circ })^{\otimes p-1}$
and
$(\unicode[STIX]{x1D6EF}^{\circ })^{\otimes p-1}$
and
![]() $\unicode[STIX]{x1D6EF}^{\otimes p-1}$
are isomorphic to
$\unicode[STIX]{x1D6EF}^{\otimes p-1}$
are isomorphic to
![]() ${\unicode[STIX]{x1D70F}_{X/k}}^{\otimes (p-1)(p-2)/2}$
, which thus implies that
${\unicode[STIX]{x1D70F}_{X/k}}^{\otimes (p-1)(p-2)/2}$
, which thus implies that
![]() $\unicode[STIX]{x1D6FF}\stackrel{\text{def}}{=}{\mathcal{H}}om_{{\mathcal{O}}_{X}}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D6EF}^{\circ })$
is of order
$\unicode[STIX]{x1D6FF}\stackrel{\text{def}}{=}{\mathcal{H}}om_{{\mathcal{O}}_{X}}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D6EF}^{\circ })$
is of order
![]() $p-1$
. In particular, it is immediate that if we write
$p-1$
. In particular, it is immediate that if we write
![]() $\unicode[STIX]{x1D6FF}^{F}$
for the invertible sheaf on
$\unicode[STIX]{x1D6FF}^{F}$
for the invertible sheaf on
![]() $X^{(1)}$
obtained by pulling back
$X^{(1)}$
obtained by pulling back
![]() $\unicode[STIX]{x1D6FF}$
via the natural morphism
$\unicode[STIX]{x1D6FF}$
via the natural morphism
![]() $X^{(1)}\rightarrow X$
, then it holds that
$X^{(1)}\rightarrow X$
, then it holds that
![]() $F^{\ast }\unicode[STIX]{x1D6FF}^{F}\cong \unicode[STIX]{x1D6FF}$
. Moreover, by considering the connection on
$F^{\ast }\unicode[STIX]{x1D6FF}^{F}\cong \unicode[STIX]{x1D6FF}$
. Moreover, by considering the connection on
![]() $F^{\ast }\unicode[STIX]{x1D6FF}^{F}$
determined by the factorization of Lemma 1.3(iii), we conclude that
$F^{\ast }\unicode[STIX]{x1D6FF}^{F}$
determined by the factorization of Lemma 1.3(iii), we conclude that
![]() ${\mathcal{E}}\otimes _{{\mathcal{O}}_{X}}F^{\ast }\unicode[STIX]{x1D6FF}^{F}$
determines a dormant oper that is equivalent to
${\mathcal{E}}\otimes _{{\mathcal{O}}_{X}}F^{\ast }\unicode[STIX]{x1D6FF}^{F}$
determines a dormant oper that is equivalent to
![]() $\mathfrak{E}$
. Thus, to complete the verification of Theorem 2.1, we may assume without loss of generality, by replacing
$\mathfrak{E}$
. Thus, to complete the verification of Theorem 2.1, we may assume without loss of generality, by replacing
![]() ${\mathcal{E}}$
by
${\mathcal{E}}$
by
![]() ${\mathcal{E}}\otimes _{{\mathcal{O}}_{X}}F^{\ast }\unicode[STIX]{x1D6FF}^{F}$
, that
${\mathcal{E}}\otimes _{{\mathcal{O}}_{X}}F^{\ast }\unicode[STIX]{x1D6FF}^{F}$
, that
By means of such an isomorphism, let us identify
![]() $\unicode[STIX]{x1D6EF}^{\circ }$
with
$\unicode[STIX]{x1D6EF}^{\circ }$
with
![]() $\unicode[STIX]{x1D6EF}$
.
$\unicode[STIX]{x1D6EF}$
.
Next, let us observe that since the
![]() $p$
-curvature of
$p$
-curvature of
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
is zero, and
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
is zero, and
![]() $(\det {\mathcal{E}},\det \unicode[STIX]{x1D6FB}_{{\mathcal{E}}})$
is isomorphic to
$(\det {\mathcal{E}},\det \unicode[STIX]{x1D6FB}_{{\mathcal{E}}})$
is isomorphic to
![]() $({\mathcal{O}}_{X},d)$
, it follows from a theorem of Cartier (cf., e.g., [Reference Katz6, Theorem 5.1]) that if we write
$({\mathcal{O}}_{X},d)$
, it follows from a theorem of Cartier (cf., e.g., [Reference Katz6, Theorem 5.1]) that if we write
![]() ${\mathcal{F}}\stackrel{\text{def}}{=}{\mathcal{E}}^{\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}}$
for the
${\mathcal{F}}\stackrel{\text{def}}{=}{\mathcal{E}}^{\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}}$
for the
![]() ${\mathcal{O}}_{X^{(1)}}$
-module of horizontal sections of
${\mathcal{O}}_{X^{(1)}}$
-module of horizontal sections of
![]() ${\mathcal{E}}$
with respect to
${\mathcal{E}}$
with respect to
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
, then
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
, then
(a)
 ${\mathcal{E}}$
is naturally isomorphic to
${\mathcal{E}}$
is naturally isomorphic to
 $F^{\ast }{\mathcal{F}}$
;
$F^{\ast }{\mathcal{F}}$
;(b) the connection
 $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
arises from the isomorphism of (a) (together with the factorization of Lemma 1.3(iii)); and
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
arises from the isomorphism of (a) (together with the factorization of Lemma 1.3(iii)); and(c)
 $\det {\mathcal{F}}$
is isomorphic to
$\det {\mathcal{F}}$
is isomorphic to
 ${\mathcal{O}}_{X^{(1)}}$
.
${\mathcal{O}}_{X^{(1)}}$
.
Thus, the isomorphism
![]() $F^{\ast }{\mathcal{F}}\stackrel{{\sim}}{\rightarrow }{\mathcal{E}}$
of (a) and the surjection
$F^{\ast }{\mathcal{F}}\stackrel{{\sim}}{\rightarrow }{\mathcal{E}}$
of (a) and the surjection
![]() ${\mathcal{E}}{\twoheadrightarrow}\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}^{\circ }$
determine a surjection of
${\mathcal{E}}{\twoheadrightarrow}\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}^{\circ }$
determine a surjection of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
and hence also a homomorphism of
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules
${\mathcal{O}}_{X^{(1)}}$
-modules
Lemma 2.2. The above homomorphism
![]() ${\mathcal{F}}\rightarrow F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }$
is a locally split injection.
${\mathcal{F}}\rightarrow F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }$
is a locally split injection.
Proof. Let us first observe that it is immediate that, to verify Lemma 2.2, it suffices to verify that the homomorphism
![]() $\unicode[STIX]{x1D6FE}:{\mathcal{E}}\stackrel{{\sim}}{\leftarrow }F^{\ast }{\mathcal{F}}\rightarrow {\mathcal{G}}\stackrel{\text{def}}{=}F^{\ast }F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }$
of
$\unicode[STIX]{x1D6FE}:{\mathcal{E}}\stackrel{{\sim}}{\leftarrow }F^{\ast }{\mathcal{F}}\rightarrow {\mathcal{G}}\stackrel{\text{def}}{=}F^{\ast }F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }$
of
![]() ${\mathcal{O}}_{X}$
-modules obtained by pulling back, via
${\mathcal{O}}_{X}$
-modules obtained by pulling back, via
![]() $F$
, the homomorphism under consideration is a split injection. Next, let us observe that it follows immediately from the various definitions involved that the composite of
$F$
, the homomorphism under consideration is a split injection. Next, let us observe that it follows immediately from the various definitions involved that the composite of
![]() $\unicode[STIX]{x1D6FE}$
and the natural homomorphism
$\unicode[STIX]{x1D6FE}$
and the natural homomorphism
![]() ${\mathcal{G}}=F^{\ast }F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }\rightarrow \unicode[STIX]{x1D6EF}^{\circ }$
coincides with the natural surjection
${\mathcal{G}}=F^{\ast }F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }\rightarrow \unicode[STIX]{x1D6EF}^{\circ }$
coincides with the natural surjection
![]() ${\mathcal{E}}{\twoheadrightarrow}\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}^{\circ }$
.
${\mathcal{E}}{\twoheadrightarrow}\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}^{\circ }$
.
We write
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}$
for the connection on
$\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}$
for the connection on
![]() ${\mathcal{G}}$
determined by the factorization of Lemma 1.3(iii). Thus, it follows immediately from the definitions of
${\mathcal{G}}$
determined by the factorization of Lemma 1.3(iii). Thus, it follows immediately from the definitions of
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
and
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
and
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}$
that
$\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}$
that
![]() $\unicode[STIX]{x1D6FE}$
is horizontal with respect to
$\unicode[STIX]{x1D6FE}$
is horizontal with respect to
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
and
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
and
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}$
. Moreover, for
$\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}$
. Moreover, for
![]() $i\in \{1,\ldots ,p\}$
, let us define submodules
$i\in \{1,\ldots ,p\}$
, let us define submodules
![]() ${\mathcal{G}}_{i}\subseteq {\mathcal{G}}$
inductively as follows. We shall write
${\mathcal{G}}_{i}\subseteq {\mathcal{G}}$
inductively as follows. We shall write
![]() ${\mathcal{G}}_{1}\stackrel{\text{def}}{=}\text{Ker}({\mathcal{G}}=F^{\ast }F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }{\twoheadrightarrow}\unicode[STIX]{x1D6EF}^{\circ })$
. If
${\mathcal{G}}_{1}\stackrel{\text{def}}{=}\text{Ker}({\mathcal{G}}=F^{\ast }F_{\ast }\unicode[STIX]{x1D6EF}^{\circ }{\twoheadrightarrow}\unicode[STIX]{x1D6EF}^{\circ })$
. If
![]() $i\geqslant 2$
, then we shall write
$i\geqslant 2$
, then we shall write
![]() ${\mathcal{G}}_{i}\stackrel{\text{def}}{=}\text{Ker}({\mathcal{G}}_{i-1}{\hookrightarrow}{\mathcal{G}}\stackrel{\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}}{\rightarrow }{\mathcal{G}}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}{\twoheadrightarrow}({\mathcal{G}}/{\mathcal{G}}_{i-1})\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k})$
. Then, it follows that the submodule
${\mathcal{G}}_{i}\stackrel{\text{def}}{=}\text{Ker}({\mathcal{G}}_{i-1}{\hookrightarrow}{\mathcal{G}}\stackrel{\unicode[STIX]{x1D6FB}_{{\mathcal{G}}}}{\rightarrow }{\mathcal{G}}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}{\twoheadrightarrow}({\mathcal{G}}/{\mathcal{G}}_{i-1})\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k})$
. Then, it follows that the submodule
![]() ${\mathcal{G}}_{i}\subseteq {\mathcal{G}}$
is an
${\mathcal{G}}_{i}\subseteq {\mathcal{G}}$
is an
![]() ${\mathcal{O}}_{X}$
-submodule, and
${\mathcal{O}}_{X}$
-submodule, and
![]() ${\mathcal{G}}_{p}=\{0\}$
. Moreover, it follows immediately from a local explicit calculation (cf. also [Reference Joshi and Pauly5, Theorem 3.1.6]) that the collection of data
${\mathcal{G}}_{p}=\{0\}$
. Moreover, it follows immediately from a local explicit calculation (cf. also [Reference Joshi and Pauly5, Theorem 3.1.6]) that the collection of data
satisfies conditions (1), (2), (3), and (4) of Definition 1.1.
Now, I claim that the following assertion holds.
For each
![]() $i\in \{1,\ldots ,p-1\}$
, the composite
$i\in \{1,\ldots ,p-1\}$
, the composite
![]() ${\mathcal{E}}_{i-1}{\hookrightarrow}{\mathcal{E}}\stackrel{\unicode[STIX]{x1D6FE}}{\rightarrow }{\mathcal{G}}$
determines an isomorphism
${\mathcal{E}}_{i-1}{\hookrightarrow}{\mathcal{E}}\stackrel{\unicode[STIX]{x1D6FE}}{\rightarrow }{\mathcal{G}}$
determines an isomorphism
![]() ${\mathcal{E}}_{i-1}/{\mathcal{E}}_{i}\stackrel{{\sim}}{\rightarrow }{\mathcal{G}}_{i-1}/{\mathcal{G}}_{i}$
of
${\mathcal{E}}_{i-1}/{\mathcal{E}}_{i}\stackrel{{\sim}}{\rightarrow }{\mathcal{G}}_{i-1}/{\mathcal{G}}_{i}$
of
![]() ${\mathcal{O}}_{X}$
-modules.
${\mathcal{O}}_{X}$
-modules.
Let us verify this claim by induction on
![]() $i$
. If
$i$
. If
![]() $i=1$
, then the desired assertion has already been verified (in the first paragraph of this proof). Let
$i=1$
, then the desired assertion has already been verified (in the first paragraph of this proof). Let
![]() $i\in \{2,\ldots ,p-1\}$
. Suppose that
$i\in \{2,\ldots ,p-1\}$
. Suppose that
![]() $\unicode[STIX]{x1D6FE}$
determines an isomorphism
$\unicode[STIX]{x1D6FE}$
determines an isomorphism
![]() ${\mathcal{E}}_{i-2}/{\mathcal{E}}_{i-1}\stackrel{{\sim}}{\rightarrow }{\mathcal{G}}_{i-2}/{\mathcal{G}}_{i-1}$
of
${\mathcal{E}}_{i-2}/{\mathcal{E}}_{i-1}\stackrel{{\sim}}{\rightarrow }{\mathcal{G}}_{i-2}/{\mathcal{G}}_{i-1}$
of
![]() ${\mathcal{O}}_{X}$
-modules, which thus implies that
${\mathcal{O}}_{X}$
-modules, which thus implies that
![]() $\unicode[STIX]{x1D6FE}({\mathcal{E}}_{i-1})\subseteq {\mathcal{G}}_{i-1}$
. Thus, since
$\unicode[STIX]{x1D6FE}({\mathcal{E}}_{i-1})\subseteq {\mathcal{G}}_{i-1}$
. Thus, since
![]() $\unicode[STIX]{x1D6FE}$
is horizontal, the diagram
$\unicode[STIX]{x1D6FE}$
is horizontal, the diagram

commutes. In particular, it follows immediately from condition (3) of Definition 1.1, together with the induction hypothesis, that
![]() $\unicode[STIX]{x1D6FE}$
determines an isomorphism
$\unicode[STIX]{x1D6FE}$
determines an isomorphism
![]() ${\mathcal{E}}_{i-1}/{\mathcal{E}}_{i}\stackrel{{\sim}}{\rightarrow }{\mathcal{G}}_{i-1}/{\mathcal{G}}_{i}$
of
${\mathcal{E}}_{i-1}/{\mathcal{E}}_{i}\stackrel{{\sim}}{\rightarrow }{\mathcal{G}}_{i-1}/{\mathcal{G}}_{i}$
of
![]() ${\mathcal{O}}_{X}$
-modules, as desired. This completes the proof of the above claim.
${\mathcal{O}}_{X}$
-modules, as desired. This completes the proof of the above claim.
It follows immediately from the above claim that the composite
![]() ${\mathcal{E}}\stackrel{\unicode[STIX]{x1D6FE}}{\rightarrow }{\mathcal{G}}{\twoheadrightarrow}{\mathcal{G}}/{\mathcal{G}}_{p-1}$
is an isomorphism of
${\mathcal{E}}\stackrel{\unicode[STIX]{x1D6FE}}{\rightarrow }{\mathcal{G}}{\twoheadrightarrow}{\mathcal{G}}/{\mathcal{G}}_{p-1}$
is an isomorphism of
![]() ${\mathcal{O}}_{X}$
-modules. In particular,
${\mathcal{O}}_{X}$
-modules. In particular,
![]() $\unicode[STIX]{x1D6FE}$
is a split injection. This completes the proof of Lemma 2.2.◻
$\unicode[STIX]{x1D6FE}$
is a split injection. This completes the proof of Lemma 2.2.◻
By Lemma 2.2, together with the fact that
![]() $\unicode[STIX]{x1D6EF}^{\circ }$
is isomorphic to
$\unicode[STIX]{x1D6EF}^{\circ }$
is isomorphic to
![]() $F^{\ast }{\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
(cf. the discussion preceding Proposition 1.4), we have an exact sequence of locally free
$F^{\ast }{\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D714}_{X/k}$
(cf. the discussion preceding Proposition 1.4), we have an exact sequence of locally free
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules
${\mathcal{O}}_{X^{(1)}}$
-modules
Lemma 2.3. The above
![]() ${\mathcal{O}}_{X^{(1)}}$
-module
${\mathcal{O}}_{X^{(1)}}$
-module
![]() ${\mathcal{Q}}$
is isomorphic to
${\mathcal{Q}}$
is isomorphic to
![]() ${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}\unicode[STIX]{x1D714}_{X^{(1)}/k}$
.
${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}\unicode[STIX]{x1D714}_{X^{(1)}/k}$
.
Proof. Let us first observe that
![]() ${\mathcal{F}}$
is of rank
${\mathcal{F}}$
is of rank
![]() $p-1$
, and
$p-1$
, and
![]() ${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}F_{\ast }\unicode[STIX]{x1D714}_{X/k}$
is of rank
${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}F_{\ast }\unicode[STIX]{x1D714}_{X/k}$
is of rank
![]() $p$
, which thus implies that
$p$
, which thus implies that
![]() ${\mathcal{Q}}$
is an invertible sheaf on
${\mathcal{Q}}$
is an invertible sheaf on
![]() $X^{(1)}$
. Thus, by the exact sequence of the discussion preceding Lemma 2.3, together with (c) of the discussion preceding Lemma 2.2, it holds that
$X^{(1)}$
. Thus, by the exact sequence of the discussion preceding Lemma 2.3, together with (c) of the discussion preceding Lemma 2.2, it holds that
In particular, since (it follows from our choice of
![]() ${\mathcal{L}}^{\circ }$
– cf. Lemma 1.3(ix) – that)
${\mathcal{L}}^{\circ }$
– cf. Lemma 1.3(ix) – that)
![]() $({\mathcal{L}}^{\circ })^{\otimes p-1}$
is isomorphic to
$({\mathcal{L}}^{\circ })^{\otimes p-1}$
is isomorphic to
![]() ${\mathcal{H}}om_{{\mathcal{O}}_{X^{(1)}}}(\det B_{1},{\mathcal{O}}_{X^{(1)}})$
, we obtain that
${\mathcal{H}}om_{{\mathcal{O}}_{X^{(1)}}}(\det B_{1},{\mathcal{O}}_{X^{(1)}})$
, we obtain that
Next, let us recall (cf., e.g., [Reference Katz6, Theorem 7.2]) the well-known exact sequence of
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules
${\mathcal{O}}_{X^{(1)}}$
-modules
where we write
![]() $c$
for the Cartier operator. Thus, it follows from the definition of
$c$
for the Cartier operator. Thus, it follows from the definition of
![]() $B_{1}$
that
$B_{1}$
that
This completes the proof of Lemma 2.3. ◻
By Lemma 2.3, we have an exact sequence of locally free
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules
${\mathcal{O}}_{X^{(1)}}$
-modules
On the other hand, we have an exact sequence of locally free
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules
${\mathcal{O}}_{X^{(1)}}$
-modules
(cf. the well-known exact sequence that appears in the second paragraph of the proof of Lemma 2.3).
Let us complete the proof of Theorem 2.1.
Proof of Theorem 2.1.
Now, I claim that the following assertion holds.
Every homomorphism
![]() $F_{\ast }\unicode[STIX]{x1D714}_{X/k}\rightarrow \unicode[STIX]{x1D714}_{X^{(1)}/k}$
of
$F_{\ast }\unicode[STIX]{x1D714}_{X/k}\rightarrow \unicode[STIX]{x1D714}_{X^{(1)}/k}$
of
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules is a
${\mathcal{O}}_{X^{(1)}}$
-modules is a
![]() $k$
-multiple of the Cartier operator
$k$
-multiple of the Cartier operator
![]() $c$
(cf. the well-known exact sequence that appears in the second paragraph of the proof of Lemma 2.3).
$c$
(cf. the well-known exact sequence that appears in the second paragraph of the proof of Lemma 2.3).
Indeed, it follows immediately from a local explicit calculation that the map
![]() $F_{\ast }{\mathcal{O}}_{X}\times F_{\ast }\unicode[STIX]{x1D714}_{X/k}\rightarrow \unicode[STIX]{x1D714}_{X^{(1)}/k}$
given by mapping
$F_{\ast }{\mathcal{O}}_{X}\times F_{\ast }\unicode[STIX]{x1D714}_{X/k}\rightarrow \unicode[STIX]{x1D714}_{X^{(1)}/k}$
given by mapping
![]() $(f,\unicode[STIX]{x1D703})$
to
$(f,\unicode[STIX]{x1D703})$
to
![]() $c(f\cdot \unicode[STIX]{x1D703})$
determines an isomorphism
$c(f\cdot \unicode[STIX]{x1D703})$
determines an isomorphism
![]() $F_{\ast }{\mathcal{O}}_{X}\stackrel{{\sim}}{\rightarrow }{\mathcal{H}}om_{{\mathcal{O}}_{X^{(1)}}}(F_{\ast }\unicode[STIX]{x1D714}_{X/k},\unicode[STIX]{x1D714}_{X^{(1)}/k})$
of
$F_{\ast }{\mathcal{O}}_{X}\stackrel{{\sim}}{\rightarrow }{\mathcal{H}}om_{{\mathcal{O}}_{X^{(1)}}}(F_{\ast }\unicode[STIX]{x1D714}_{X/k},\unicode[STIX]{x1D714}_{X^{(1)}/k})$
of
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules (cf. also the discussion preceding [Reference Raynaud8, Théorème 4.1.1]). Thus, the above claim follows from the fact that
${\mathcal{O}}_{X^{(1)}}$
-modules (cf. also the discussion preceding [Reference Raynaud8, Théorème 4.1.1]). Thus, the above claim follows from the fact that
![]() $\unicode[STIX]{x1D6E4}(X^{(1)},{\mathcal{H}}om_{{\mathcal{O}}_{X^{(1)}}}(F_{\ast }\unicode[STIX]{x1D714}_{X/k},\unicode[STIX]{x1D714}_{X^{(1)}/k}))\cong \unicode[STIX]{x1D6E4}(X^{(1)},F_{\ast }{\mathcal{O}}_{X^{(1)}})\cong \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
is of dimension one. This completes the proof of the above claim.
$\unicode[STIX]{x1D6E4}(X^{(1)},{\mathcal{H}}om_{{\mathcal{O}}_{X^{(1)}}}(F_{\ast }\unicode[STIX]{x1D714}_{X/k},\unicode[STIX]{x1D714}_{X^{(1)}/k}))\cong \unicode[STIX]{x1D6E4}(X^{(1)},F_{\ast }{\mathcal{O}}_{X^{(1)}})\cong \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
is of dimension one. This completes the proof of the above claim.
Let us recall the two exact sequences of
![]() ${\mathcal{O}}_{X^{(1)}}$
-modules
${\mathcal{O}}_{X^{(1)}}$
-modules
appearing in the discussion following Lemma 2.3. It follows immediately from the above claim that we have an equality
![]() ${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}B_{1}={\mathcal{F}}$
(in
${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}B_{1}={\mathcal{F}}$
(in
![]() ${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}F_{\ast }\unicode[STIX]{x1D714}_{X/k}$
). In particular, we have an isomorphism
${\mathcal{L}}^{\circ }\otimes _{{\mathcal{O}}_{X^{(1)}}}F_{\ast }\unicode[STIX]{x1D714}_{X/k}$
). In particular, we have an isomorphism
![]() $\unicode[STIX]{x1D719}:{\mathcal{E}}^{\circ }\stackrel{{\sim}}{\rightarrow }{\mathcal{E}}$
(i.e.,
$\unicode[STIX]{x1D719}:{\mathcal{E}}^{\circ }\stackrel{{\sim}}{\rightarrow }{\mathcal{E}}$
(i.e.,
![]() $F^{\ast }\text{id}$
). Moreover, it follows immediately from the definition of
$F^{\ast }\text{id}$
). Moreover, it follows immediately from the definition of
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
, together with (b) of the discussion preceding Lemma 2.2, that the isomorphism
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
, together with (b) of the discussion preceding Lemma 2.2, that the isomorphism
![]() $\unicode[STIX]{x1D719}$
is horizontal with respect to
$\unicode[STIX]{x1D719}$
is horizontal with respect to
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
,
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}^{\circ }}^{\text{can}}$
,
![]() $\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
.
$\unicode[STIX]{x1D6FB}_{{\mathcal{E}}}$
.
Finally, we verify that
![]() $\unicode[STIX]{x1D719}({\mathcal{E}}_{p-i}^{\circ })={\mathcal{E}}_{p-i}$
for each
$\unicode[STIX]{x1D719}({\mathcal{E}}_{p-i}^{\circ })={\mathcal{E}}_{p-i}$
for each
![]() $i\in \{1,\ldots ,p-1\}$
by induction on
$i\in \{1,\ldots ,p-1\}$
by induction on
![]() $i$
. The equality
$i$
. The equality
![]() $(\{0\}=)$
$(\{0\}=)$
![]() $\unicode[STIX]{x1D719}({\mathcal{E}}_{p-1}^{\circ })={\mathcal{E}}_{p-1}$
$\unicode[STIX]{x1D719}({\mathcal{E}}_{p-1}^{\circ })={\mathcal{E}}_{p-1}$
![]() $(=\{0\})$
is immediate. Let
$(=\{0\})$
is immediate. Let
![]() $i\in \{2,\ldots ,p-1\}$
. Suppose that
$i\in \{2,\ldots ,p-1\}$
. Suppose that
![]() $\unicode[STIX]{x1D719}({\mathcal{E}}_{p-i+1}^{\circ })={\mathcal{E}}_{p-i+1}$
holds. Then, to verify that
$\unicode[STIX]{x1D719}({\mathcal{E}}_{p-i+1}^{\circ })={\mathcal{E}}_{p-i+1}$
holds. Then, to verify that
![]() $\unicode[STIX]{x1D719}({\mathcal{E}}_{p-i}^{\circ })={\mathcal{E}}_{p-i}$
, it suffices to verify that the induced isomorphism
$\unicode[STIX]{x1D719}({\mathcal{E}}_{p-i}^{\circ })={\mathcal{E}}_{p-i}$
, it suffices to verify that the induced isomorphism
![]() ${\mathcal{E}}^{\circ }/{\mathcal{E}}_{p-i+1}^{\circ }\stackrel{{\sim}}{\rightarrow }{\mathcal{E}}/{\mathcal{E}}_{p-i+1}$
maps
${\mathcal{E}}^{\circ }/{\mathcal{E}}_{p-i+1}^{\circ }\stackrel{{\sim}}{\rightarrow }{\mathcal{E}}/{\mathcal{E}}_{p-i+1}$
maps
![]() ${\mathcal{E}}_{p-i}^{\circ }/{\mathcal{E}}_{p-i+1}^{\circ }$
isomorphically onto
${\mathcal{E}}_{p-i}^{\circ }/{\mathcal{E}}_{p-i+1}^{\circ }$
isomorphically onto
![]() ${\mathcal{E}}_{p-i}/{\mathcal{E}}_{p-i+1}$
. On the other hand, since (it follows immediately from the definition of a dormant oper that)
${\mathcal{E}}_{p-i}/{\mathcal{E}}_{p-i+1}$
. On the other hand, since (it follows immediately from the definition of a dormant oper that)
for each
![]() $j\in \{1,\ldots ,p-1\}$
, the desired assertion follows immediately from the ampleness of
$j\in \{1,\ldots ,p-1\}$
, the desired assertion follows immediately from the ampleness of
![]() $\unicode[STIX]{x1D714}_{X/k}$
. This completes the proof of Theorem 2.1.◻
$\unicode[STIX]{x1D714}_{X/k}$
. This completes the proof of Theorem 2.1.◻
Acknowledgments
The author would like to thank Akio Tamagawa for discussions concerning removal of the hypothesis that the Jacobian variety of the curve under consideration is ordinary from the main result in an earlier version of the manuscript. The author would like to thank Yasuhiro Wakabayashi for explaining basic facts concerning dormant opers. The author also would like to thank the referee for comments concerning Remark 1.4.2 and Remark 2.1.2.