Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sagle, Arthur A.
1968.
On Homogeneous Spaces, Holonomy, and Non-Associative Algebras.
Nagoya Mathematical Journal,
Vol. 32,
Issue. ,
p.
373.
Sagle, Arthur A.
1970.
Some Homogeneous Einstein Manifolds.
Nagoya Mathematical Journal,
Vol. 39,
Issue. ,
p.
81.
1972.
Lie Gronps, Principal Bundles, and Characteristic Classes.
Vol. 47,
Issue. ,
p.
511.
Alekseevskii, D. V.
1975.
Lie groups and homogeneous spaces.
Journal of Soviet Mathematics,
Vol. 4,
Issue. 5,
p.
483.
Myung, Hyo Chul
and
Sagle, Arthur A.
1988.
On the construction of reductive Lie-admissible algebras.
Journal of Pure and Applied Algebra,
Vol. 53,
Issue. 1-2,
p.
75.
Mikheev, P. O.
and
Sabinin, L. V.
1990.
Smooth quasigroups and geometry.
Journal of Soviet Mathematics,
Vol. 51,
Issue. 6,
p.
2642.
Benito, Pilar
Draper, Cristina
and
Elduque, Alberto
2005.
Lie–Yamaguti algebras related to g2.
Journal of Pure and Applied Algebra,
Vol. 202,
Issue. 1-3,
p.
22.
Benito, Pilar
Elduque, Alberto
and
Martín-Herce, Fabián
2009.
Irreducible Lie–Yamaguti algebras.
Journal of Pure and Applied Algebra,
Vol. 213,
Issue. 5,
p.
795.
Benito, Pilar
Elduque, Alberto
and
Martín-Herce, Fabián
2011.
Irreducible Lie–Yamaguti algebras of generic type.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 2,
p.
108.
Benito, Pilar
Bremner, Murray
and
Madariaga, Sara
2015.
Symmetric matrices, orthogonal Lie algebras and Lie-Yamaguti algebras.
Linear and Multilinear Algebra,
Vol. 63,
Issue. 6,
p.
1257.
Lin, Jie
Chen, Liang Yun
and
Ma, Yao
2015.
On the deformation of Lie-Yamaguti algebras.
Acta Mathematica Sinica, English Series,
Vol. 31,
Issue. 6,
p.
938.
Lakshmi Devi, G.
and
Jayalakshmi, K.
2018.
A reductive case on derivations in Vinberg (−1,1) rings.
Asian-European Journal of Mathematics,
Vol. 11,
Issue. 03,
p.
1850037.
Lin, Jie
and
Chen, Liangyun
2023.
Quasi-derivations of Lie–Yamaguti algebras.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 05,
Goswami, Saikat
Mishra, Satyendra Kumar
and
Mukherjee, Goutam
2024.
Automorphisms of extensions of Lie-Yamaguti algebras and inducibility problem.
Journal of Algebra,
Vol. 641,
Issue. ,
p.
268.
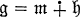 (subspace direct sum) with
(subspace direct sum) with 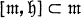 where g (resp.
where g (resp. 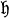 ) is the Lie algebra of G (resp. H); in this case the pair (g,
) is the Lie algebra of G (resp. H); in this case the pair (g,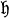 ) is called a reductive pair.
) is called a reductive pair.



