Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-08T22:29:28.105Z Has data issue: false hasContentIssue false
  • English
  • Français

On Positive Solutions of the Heat Equation

Published online by Cambridge University Press:  22 January 2016

Masasumi Kato
Masasumi Kato*
Affiliation:
Suzuka College of Technology
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the positive and twice continuously differentiable solutions u of the heat equation

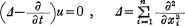
in an open t-strip Ω = Rn×(0,T) for some T>0, where Rn is the n-dimensional Euclidean space.

In this note, we prove a theorem of Fatou type on u and, as its application, the uniqueness theorem for the Cauchy problem of ( 1 ).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 30 , August 1967 , pp. 203 - 207
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Dressel, F.G.: The fundamental solution of the parabolic equation. Duke Math. J., 7 (1940) 186-203, 13 (1946) 61–70.CrossRefGoogle Scholar
[2] Friedman, A.: Partial differential equations of parabolic type. Prentice-Hall (1964).Google Scholar
[3] Rosenbloom, P.C.: Linear equations of parabolic type with constant coefficients. Contributions to the theory of partial differential equations. Ann. Math. Studies, no. 33 (Princeton Univ. Press, 1954), p. 191–200.Google Scholar
[4] Saks, S.: Theory of the integral. Warsaw. (1937).Google Scholar
[5] Widder, D.V.: Positive temperatures on an infinite rod. Tran. Amer. Math. Soc, 55, 85–95 (1944).CrossRefGoogle Scholar