Hostname: page-component-84b7d79bbc-rnpqb Total loading time: 0 Render date: 2024-07-31T16:17:41.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Picard principle for finite densities on some end

Published online by Cambridge University Press:  22 January 2016

Michihiko Kawamura
Michihiko Kawamura*
Affiliation:
Mathematical Institute, Faculty of Education, Fukui University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a parabolic end Ω of a Riemann surface in the sence of Heins [2] (cf. Nakai [3]). A density P = P(z)dxdy (z = x + iy) is a 2-form on 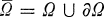with nonnegative locally Hölder continuous coefficients P(z). A density P is said to be finite if the integral

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 67 , August 1977 , pp. 35 - 40
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1977

References

[1] Hayashi, K.: Les solutions positive de léquation Γu=Pu sur une surface de Riemann, Kōdai Math. Sem. Rep., 13 (1961), 20–24.Google Scholar
[2] Heins, M.: Riemann surfaces of infinite genus, Ann. Math., 55 (1952), 296–317.CrossRefGoogle Scholar
[3] Nakai, M.: Martin boundary over an isolated singularity of rotation free density, J. Math. Soc. Japan, 26 (1974), 483–507.CrossRefGoogle Scholar
[4] Nakai, M.: A test for Picard principle, Nagoya Math. J., 56 (1974), 105–119.CrossRefGoogle Scholar
[5] Nakai, M.: Picard principle and Riemann theorem, Tôhoku Math. J., 28 (1976), 277–292.CrossRefGoogle Scholar
[6] Nakai, M.: Picard principle for finite densities, Nagoya Math. J., vol.70 (1978) (to appear).CrossRefGoogle Scholar
[7] Nakai, M.: A remark on Picard principle II, Proc. Japan Acad., 51 (1975), 308–311.Google Scholar