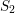1 Introduction
Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
. We say that
$d\geqslant 1$
. We say that
![]() $\mathbf{R}$
is almost Cohen–Macaulay, or, briefly, aCM, if
$\mathbf{R}$
is almost Cohen–Macaulay, or, briefly, aCM, if
![]() $\text{depth}~~\mathbf{R}\geqslant d-1$
. Numerous classes of such rings occur among Rees algebras of ideals of Cohen–Macaulay rings (addressed in several classical papers of Sally, Valla and others; see the surveys [Reference Rossi and Valla23, Reference Sally24]). They also arise in the normalization of integral domains of low dimension and among rings of invariants. Obviously, information about the aCM condition rests in the cohomology of the algebra, which often is not fully available. As a corrective, we look for chunks of those data that may be available in the reduction number of the ideal, Hilbert coefficients, structure of the Sally module and in the relationships among these invariants.
$\text{depth}~~\mathbf{R}\geqslant d-1$
. Numerous classes of such rings occur among Rees algebras of ideals of Cohen–Macaulay rings (addressed in several classical papers of Sally, Valla and others; see the surveys [Reference Rossi and Valla23, Reference Sally24]). They also arise in the normalization of integral domains of low dimension and among rings of invariants. Obviously, information about the aCM condition rests in the cohomology of the algebra, which often is not fully available. As a corrective, we look for chunks of those data that may be available in the reduction number of the ideal, Hilbert coefficients, structure of the Sally module and in the relationships among these invariants.
The simplest to describe of these notions is that of reductions of ideals, but we only make use of a special case. For simplicity, we assume that the residue field
![]() $\mathbf{R}/\mathfrak{m}$
is infinite. If
$\mathbf{R}/\mathfrak{m}$
is infinite. If
![]() $I$
is an
$I$
is an
![]() $\mathfrak{m}$
-primary ideal, a minimal reduction is an ideal
$\mathfrak{m}$
-primary ideal, a minimal reduction is an ideal
![]() $Q=(a_{1},\ldots ,a_{d})\subset I$
such that
$Q=(a_{1},\ldots ,a_{d})\subset I$
such that
![]() $I^{n+1}=QI^{n}$
for some integer
$I^{n+1}=QI^{n}$
for some integer
![]() $n\geqslant 0$
. The smallest such integer is denoted
$n\geqslant 0$
. The smallest such integer is denoted
![]() $\text{r}_{Q}(I)$
and called the reduction number of
$\text{r}_{Q}(I)$
and called the reduction number of
![]() $I$
relative to
$I$
relative to
![]() $Q$
. We set
$Q$
. We set
![]() $\text{r}(I)=\inf \{\text{r}_{Q}(I)\mid Q\;\text{is a minimal reduction of}\;I\}$
. A set of questions revolves around the relationship between the Hilbert coefficients of
$\text{r}(I)=\inf \{\text{r}_{Q}(I)\mid Q\;\text{is a minimal reduction of}\;I\}$
. A set of questions revolves around the relationship between the Hilbert coefficients of
![]() $I$
and its reduction number. In turn, the mentioned coefficients are those extracted from the Hilbert function of
$I$
and its reduction number. In turn, the mentioned coefficients are those extracted from the Hilbert function of
![]() $I$
; that is, of the associated graded ring
$I$
; that is, of the associated graded ring
![]() $\text{gr}_{I}(\mathbf{R})=\bigoplus _{n\geqslant 0}I^{n}/I^{n+1}$
, or, more precisely, from some of the coefficients of its Hilbert polynomial
$\text{gr}_{I}(\mathbf{R})=\bigoplus _{n\geqslant 0}I^{n}/I^{n+1}$
, or, more precisely, from some of the coefficients of its Hilbert polynomial
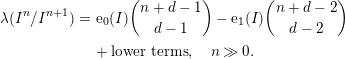 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}(I^{n}/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d-1}{d-1}-\text{e}_{1}(I)\binom{n+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\,\text{lower terms},\quad n\gg 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}(I^{n}/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d-1}{d-1}-\text{e}_{1}(I)\binom{n+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\,\text{lower terms},\quad n\gg 0.\nonumber\end{eqnarray}$$
An instance of the relationships between these invariants of
![]() $I$
is the following. If
$I$
is the following. If
![]() $\mathbf{R}$
is Cohen–Macaulay, we have from [Reference Vasconcelos29, Theorem 2.45]
$\mathbf{R}$
is Cohen–Macaulay, we have from [Reference Vasconcelos29, Theorem 2.45]
where
![]() $\text{e}_{0}(I)$
is the multiplicity of
$\text{e}_{0}(I)$
is the multiplicity of
![]() $I$
and
$I$
and
![]() $o(I)$
is the order of
$o(I)$
is the order of
![]() $I$
; that is, the largest positive integer
$I$
; that is, the largest positive integer
![]() $n$
such that
$n$
such that
![]() $I\subset \mathfrak{m}^{n}$
. A non-Cohen–Macaulay version of similar character is given in [Reference Ghezzi, Goto, Hong and Vasconcelos8, Theorem 3.3], with
$I\subset \mathfrak{m}^{n}$
. A non-Cohen–Macaulay version of similar character is given in [Reference Ghezzi, Goto, Hong and Vasconcelos8, Theorem 3.3], with
![]() $\text{e}_{0}(I)$
replaced by
$\text{e}_{0}(I)$
replaced by
![]() $\unicode[STIX]{x1D706}(\mathbf{R}/Q)$
for any reduction
$\unicode[STIX]{x1D706}(\mathbf{R}/Q)$
for any reduction
![]() $Q$
of
$Q$
of
![]() $I$
. Since
$I$
. Since
![]() $\unicode[STIX]{x1D706}(\mathbf{R}/Q)=\text{e}_{0}(I)+\unicode[STIX]{x1D712}_{1}(Q)\leqslant \text{hdeg}_{I}(\mathbf{R})$
, by Serre’s theorem [Reference Bruns and Herzog2, Theorem 4.7.10] and [Reference Ghezzi, Goto, Hong, Ozeki, Phuong and Vasconcelos9, Theorem 7.2] respectively, the reduction number
$\unicode[STIX]{x1D706}(\mathbf{R}/Q)=\text{e}_{0}(I)+\unicode[STIX]{x1D712}_{1}(Q)\leqslant \text{hdeg}_{I}(\mathbf{R})$
, by Serre’s theorem [Reference Bruns and Herzog2, Theorem 4.7.10] and [Reference Ghezzi, Goto, Hong, Ozeki, Phuong and Vasconcelos9, Theorem 7.2] respectively, the reduction number
![]() $\text{r}(I)$
can be bounded in terms of
$\text{r}(I)$
can be bounded in terms of
![]() $I$
alone. It is worth asking whether a sharper bound holds on replacing
$I$
alone. It is worth asking whether a sharper bound holds on replacing
![]() $\unicode[STIX]{x1D706}(\mathbf{R}/Q)$
by
$\unicode[STIX]{x1D706}(\mathbf{R}/Q)$
by
![]() $\text{e}_{0}(I)-\text{e}_{1}(Q)$
(see [Reference Goto, Hong and Vasconcelos10, Theorem 4.2]).
$\text{e}_{0}(I)-\text{e}_{1}(Q)$
(see [Reference Goto, Hong and Vasconcelos10, Theorem 4.2]).
A distinct kind of bound was introduced by Rossi [Reference Rossi22].
Theorem 1.1. [Reference Rossi22, Corollary 1.5]
If
![]() $(\mathbf{R},\mathfrak{m})$
is a Cohen–Macaulay local ring of dimension at most
$(\mathbf{R},\mathfrak{m})$
is a Cohen–Macaulay local ring of dimension at most
![]() $2$
, then, for any
$2$
, then, for any
![]() $\mathfrak{m}$
-primary ideal
$\mathfrak{m}$
-primary ideal
![]() $I$
with a minimal reduction
$I$
with a minimal reduction
![]() $Q$
,
$Q$
,
We refer to the right-hand side as the Rossi index of
![]() $I$
. The presence of the offsetting terms at times leads to smaller bounds. Before we explain how such bounds arise, it is worthwhile to point out that this has been observed in numerous cases in higher dimension. For instance, if the Rossi index is equal to
$I$
. The presence of the offsetting terms at times leads to smaller bounds. Before we explain how such bounds arise, it is worthwhile to point out that this has been observed in numerous cases in higher dimension. For instance, if the Rossi index is equal to
![]() $2$
, then equality holds in all dimensions (see [Reference Goto, Nishida and Ozeki11, Theorem 3.1]). Another case is that of all the ideals of
$2$
, then equality holds in all dimensions (see [Reference Goto, Nishida and Ozeki11, Theorem 3.1]). Another case is that of all the ideals of
![]() $k[x,y,z]$
of codimension
$k[x,y,z]$
of codimension
![]() $3$
generated by five quadrics (see [Reference Hong, Simis and Vasconcelos16, Theorem 2.1 and Proposition 2.4]).
$3$
generated by five quadrics (see [Reference Hong, Simis and Vasconcelos16, Theorem 2.1 and Proposition 2.4]).
We prove some specialized higher-dimension versions of this inequality and also propose a version of it for non-Cohen–Macaulay rings. These require a natural explanation for these sums as the multiplicities of certain modules that occur in the theory of Rees algebras. At the center of our discussion is the Sally module [Reference Vasconcelos27, Definition 2.1]
of
![]() $I$
relative to
$I$
relative to
![]() $Q$
. Its properties depend heavily on the value of
$Q$
. Its properties depend heavily on the value of
![]() $\text{r}_{Q}(I)$
and of its multiplicity, which in the Cohen–Macaulay case is given by
$\text{r}_{Q}(I)$
and of its multiplicity, which in the Cohen–Macaulay case is given by
![]() $\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)$
(see [Reference Vasconcelos27, Corollary 3.3]).
$\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)$
(see [Reference Vasconcelos27, Corollary 3.3]).
In Theorem 2.1, we give a quick presentation of some of the main properties of
![]() $S_{Q}(I)$
. Making use of a theorem of Serre [Reference Bruns and Herzog2, Theorem 4.7.10], we provide proofs that extend the assertions in [Reference Vasconcelos27] from the Cohen–Macaulay case to general rings with some provisos. Its use requires the knowledge of the dimension of
$S_{Q}(I)$
. Making use of a theorem of Serre [Reference Bruns and Herzog2, Theorem 4.7.10], we provide proofs that extend the assertions in [Reference Vasconcelos27] from the Cohen–Macaulay case to general rings with some provisos. Its use requires the knowledge of the dimension of
![]() $S_{Q}(I)$
(which is readily accessible if
$S_{Q}(I)$
(which is readily accessible if
![]() $\mathbf{R}$
is Cohen–Macaulay), for which we appeal to the assertion of Theorem 2.1(3), that if
$\mathbf{R}$
is Cohen–Macaulay), for which we appeal to the assertion of Theorem 2.1(3), that if
![]() $\dim S_{Q}(I)=d$
, then
$\dim S_{Q}(I)=d$
, then
![]() $\text{s}_{Q}(I)\leqslant \sum _{n=1}^{r-1}\unicode[STIX]{x1D706}(I^{n+1}/QI^{n})$
, where
$\text{s}_{Q}(I)\leqslant \sum _{n=1}^{r-1}\unicode[STIX]{x1D706}(I^{n+1}/QI^{n})$
, where
![]() $r=\text{r}_{Q}(I)$
and
$r=\text{r}_{Q}(I)$
and
![]() $\text{s}_{Q}(I)$
is an appropriate multiplicity of
$\text{s}_{Q}(I)$
is an appropriate multiplicity of
![]() $S_{Q}(I)$
. Furthermore,
$S_{Q}(I)$
. Furthermore,
![]() $S_{Q}(I)$
is Cohen–Macaulay if and only if equality holds. This is a direct extension of [Reference Huckaba17, Theorem 3.1] (see also [Reference Huckaba and Marley18, Theorem 4.7]) if
$S_{Q}(I)$
is Cohen–Macaulay if and only if equality holds. This is a direct extension of [Reference Huckaba17, Theorem 3.1] (see also [Reference Huckaba and Marley18, Theorem 4.7]) if
![]() $\mathbf{R}$
is Cohen–Macaulay. In these cases, the Rossi index of
$\mathbf{R}$
is Cohen–Macaulay. In these cases, the Rossi index of
![]() $I$
is
$I$
is
![]() $\text{s}_{Q}(I)+1$
and
$\text{s}_{Q}(I)+1$
and
![]() $\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1$
.
$\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1$
.
We want to take as our starting point the value of
![]() $\text{s}_{Q}(I)$
. We first give a change of rings result (Theorem 2.6) to detect when
$\text{s}_{Q}(I)$
. We first give a change of rings result (Theorem 2.6) to detect when
![]() $\dim S_{Q}(I)<d$
whenever we have a finite integral extension of
$\dim S_{Q}(I)<d$
whenever we have a finite integral extension of
![]() $\mathbf{R}$
into a Cohen–Macaulay ring
$\mathbf{R}$
into a Cohen–Macaulay ring
![]() $\mathbb{S}$
. This is used in Section 4 when we prove a version of Theorem 1.1 for Buchsbaum rings (Theorem 4.3).
$\mathbb{S}$
. This is used in Section 4 when we prove a version of Theorem 1.1 for Buchsbaum rings (Theorem 4.3).
Section 3 deals exclusively with almost complete intersections and derives reduction number bounds from the behavior of one component of the fiber of
![]() $S_{Q}(I)$
. For instance, if
$S_{Q}(I)$
. For instance, if
![]() $(\mathbf{R},\mathfrak{m})$
is a Noetherian local ring,
$(\mathbf{R},\mathfrak{m})$
is a Noetherian local ring,
![]() $I$
is an
$I$
is an
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $Q$
is one of its minimal reductions, then if
$Q$
is one of its minimal reductions, then if
![]() $\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
for some integer
$\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
for some integer
![]() $n>0$
, we have that
$n>0$
, we have that
![]() $\text{r}(I)\leqslant n\unicode[STIX]{x1D708}(\mathfrak{m})-1$
(Proposition 3.1).
$\text{r}(I)\leqslant n\unicode[STIX]{x1D708}(\mathfrak{m})-1$
(Proposition 3.1).
One of our main results (Theorem 3.7) gives a description of the properties of the special fiber ring, including a formula for its multiplicity
![]() $f_{0}(I)$
.
$f_{0}(I)$
.
Theorem 3.7. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
![]() $d\geqslant 1$
with infinite residue field, and let
$d\geqslant 1$
with infinite residue field, and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal which is an almost complete intersection. If for some minimal reduction
$\mathfrak{m}$
-primary ideal which is an almost complete intersection. If for some minimal reduction
![]() $Q$
of
$Q$
of
![]() $I$
,
$I$
,
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then
-
(1) the special fiber ring
 ${\mathcal{F}}(I)$
is Cohen–Macaulay;
${\mathcal{F}}(I)$
is Cohen–Macaulay; -
(2)
 $f_{0}(I)=\text{r}(I)+1=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
.
$f_{0}(I)=\text{r}(I)+1=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
.
This is the case if
![]() $\mathbf{R}$
is Gorenstein and
$\mathbf{R}$
is Gorenstein and
![]() $\unicode[STIX]{x1D706}(I/Q)=2$
.
$\unicode[STIX]{x1D706}(I/Q)=2$
.
An issue is whether there are extensions of these formulas for more general classes of ideals of Cohen–Macaulay rings, or even non-Cohen–Macaulay rings of dimension
![]() $2$
. With regard to the second question, in Section 4 we consider extensions of Theorem 1.1 to Buchsbaum rings. We begin by proving that any Buchsbaum local ring
$2$
. With regard to the second question, in Section 4 we consider extensions of Theorem 1.1 to Buchsbaum rings. We begin by proving that any Buchsbaum local ring
![]() $\mathbf{R}$
admits an
$\mathbf{R}$
admits an
![]() $S_{2}$
-fication
$S_{2}$
-fication
![]() $\mathbf{f}:\mathbf{R}\rightarrow \mathbb{S}$
. A surprising fact is the intrinsic construction of
$\mathbf{f}:\mathbf{R}\rightarrow \mathbb{S}$
. A surprising fact is the intrinsic construction of
![]() $\mathbb{S}$
, independent of the existence of a canonical module for
$\mathbb{S}$
, independent of the existence of a canonical module for
![]() $\mathbf{R}$
(Theorem 4.2). We make use of this morphism to derive in Theorem 4.3 a bound for the reduction numbers of the ideals of
$\mathbf{R}$
(Theorem 4.2). We make use of this morphism to derive in Theorem 4.3 a bound for the reduction numbers of the ideals of
![]() $\mathbf{R}$
, in dimension 2, in terms of the multiplicity of the Sally module
$\mathbf{R}$
, in dimension 2, in terms of the multiplicity of the Sally module
![]() $S_{Q}(I)$
and the Buchsbaum invariant of
$S_{Q}(I)$
and the Buchsbaum invariant of
![]() $\mathbf{R}$
.
$\mathbf{R}$
.
2 Sally modules and Rossi index
Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, let
$d\geqslant 1$
, let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal, and let
$\mathfrak{m}$
-primary ideal, and let
![]() $Q$
be a minimal reduction of
$Q$
be a minimal reduction of
![]() $I$
. Let
$I$
. Let
![]() $r=\text{r}_{Q}(I)$
be the reduction number of
$r=\text{r}_{Q}(I)$
be the reduction number of
![]() $I$
relative to
$I$
relative to
![]() $Q$
. Let us recall the construction of the Sally module associated to these data and show how some of its properties, originally stated for Cohen–Macaulay rings, hold in greater generality. We denote the Rees algebras of
$Q$
. Let us recall the construction of the Sally module associated to these data and show how some of its properties, originally stated for Cohen–Macaulay rings, hold in greater generality. We denote the Rees algebras of
![]() $Q$
and
$Q$
and
![]() $I$
by
$I$
by
![]() $\mathbf{R}[Q\mathbf{T}]$
and
$\mathbf{R}[Q\mathbf{T}]$
and
![]() $\mathbf{R}[I\mathbf{T}]$
respectively and consider the exact sequence of finitely generated
$\mathbf{R}[I\mathbf{T}]$
respectively and consider the exact sequence of finitely generated
![]() $\mathbf{R}[Q\mathbf{T}]$
-modules
$\mathbf{R}[Q\mathbf{T}]$
-modules
Then,
![]() $S=S_{Q}(I)=\bigoplus _{n\geqslant 1}I^{n+1}/IQ^{n}$
is the Sally module of
$S=S_{Q}(I)=\bigoplus _{n\geqslant 1}I^{n+1}/IQ^{n}$
is the Sally module of
![]() $I$
relative to
$I$
relative to
![]() $Q$
(see [Reference Vasconcelos27, Definition 2.1]). Note that
$Q$
(see [Reference Vasconcelos27, Definition 2.1]). Note that
is a finitely generated
![]() $\mathbf{R}$
-module. We refer to the component
$\mathbf{R}$
-module. We refer to the component
![]() $I^{n+1}/QI^{n}$
as the degree-
$I^{n+1}/QI^{n}$
as the degree-
![]() $n$
fiber of
$n$
fiber of
![]() $S_{Q}(I)$
. Note that for
$S_{Q}(I)$
. Note that for
![]() $1\leqslant n\leqslant r-1$
, these components do not vanish. If
$1\leqslant n\leqslant r-1$
, these components do not vanish. If
![]() $\dim S_{Q}(I)=d$
, and
$\dim S_{Q}(I)=d$
, and
![]() $Q=(a_{1},\ldots ,a_{d})$
, then the elements
$Q=(a_{1},\ldots ,a_{d})$
, then the elements
![]() $\{a_{1}\mathbf{T},\ldots ,a_{d}\mathbf{T}\}$
give a system of parameters for
$\{a_{1}\mathbf{T},\ldots ,a_{d}\mathbf{T}\}$
give a system of parameters for
![]() $S_{Q}(I)$
. We denote by
$S_{Q}(I)$
. We denote by
![]() $\text{s}_{Q}(I)=\text{e}_{0}((Q\mathbf{T}),S)$
the corresponding multiplicity. Its value is independent of
$\text{s}_{Q}(I)=\text{e}_{0}((Q\mathbf{T}),S)$
the corresponding multiplicity. Its value is independent of
![]() $Q$
if
$Q$
if
![]() $\mathbf{R}$
is Cohen–Macaulay. Let us summarize some results of [Reference Bruns and Herzog2, Reference Goto, Nishida and Ozeki12, Reference Huckaba17, Reference Vasconcelos27] in the following, which we often need in this paper.
$\mathbf{R}$
is Cohen–Macaulay. Let us summarize some results of [Reference Bruns and Herzog2, Reference Goto, Nishida and Ozeki12, Reference Huckaba17, Reference Vasconcelos27] in the following, which we often need in this paper.
Theorem 2.1. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d>0$
. Let
$d>0$
. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal, and let
$\mathfrak{m}$
-primary ideal, and let
![]() $Q$
be a minimal reduction of
$Q$
be a minimal reduction of
![]() $I$
with reduction number
$I$
with reduction number
![]() $r=\text{r}_{Q}(I)$
.
$r=\text{r}_{Q}(I)$
.
-
(1) The Sally module
 $S_{Q}(I)$
of
$S_{Q}(I)$
of
 $I$
relative to
$I$
relative to
 $Q$
is a finitely generated module over
$Q$
is a finitely generated module over
 $\mathbf{R}[Q\mathbf{T}]$
of dimension at most
$\mathbf{R}[Q\mathbf{T}]$
of dimension at most
 $d$
.
$d$
. -
(2) If
 $\mathbf{R}$
is Cohen–Macaulay, then
$\mathbf{R}$
is Cohen–Macaulay, then
 $S_{Q}(I)$
is either
$S_{Q}(I)$
is either
 $0$
or has dimension
$0$
or has dimension
 $d$
. In the latter case,
$d$
. In the latter case,
 $\mathfrak{m}\mathbf{R}[Q\mathbf{T}]$
is its only associated prime and its multiplicity (or rank) is
$\mathfrak{m}\mathbf{R}[Q\mathbf{T}]$
is its only associated prime and its multiplicity (or rank) is  $$\begin{eqnarray}\text{s}_{Q}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I).\end{eqnarray}$$
$$\begin{eqnarray}\text{s}_{Q}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I).\end{eqnarray}$$
-
(3) If
 $\dim S_{Q}(I)=d$
, then
$\dim S_{Q}(I)=d$
, then-
(a)
 $\text{s}_{Q}(I)\leqslant \sum _{n=1}^{r-1}\unicode[STIX]{x1D706}(I^{n+1}/QI^{n})$
;
$\text{s}_{Q}(I)\leqslant \sum _{n=1}^{r-1}\unicode[STIX]{x1D706}(I^{n+1}/QI^{n})$
; -
(b) the equality in (a) holds if and only if
 $S_{Q}(I)$
is Cohen–Macaulay, in which case
$S_{Q}(I)$
is Cohen–Macaulay, in which case
 $\text{r}_{Q}(I)\leqslant s_{Q}(I)+1$
;
$\text{r}_{Q}(I)\leqslant s_{Q}(I)+1$
; -
(c) if
 $\mathbf{R}$
is Cohen–Macaulay, the equality in (a) holds if and only if
$\mathbf{R}$
is Cohen–Macaulay, the equality in (a) holds if and only if
 $\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.
$\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.
-
Proof. Let
![]() $S=S_{Q}(I)$
. Since
$S=S_{Q}(I)$
. Since
![]() $\mathfrak{m}^{l}S=0$
for some integer
$\mathfrak{m}^{l}S=0$
for some integer
![]() $l>0$
[Reference Goto, Nishida and Ozeki12, Lemma 2.1],
$l>0$
[Reference Goto, Nishida and Ozeki12, Lemma 2.1],
![]() $\dim _{\mathbf{R}[Q\mathbf{T}]}(S)\leqslant d$
. The assertion (2) is proved in [Reference Vasconcelos27, Proposition 2.2, Corollary 3.3]. Now, suppose that
$\dim _{\mathbf{R}[Q\mathbf{T}]}(S)\leqslant d$
. The assertion (2) is proved in [Reference Vasconcelos27, Proposition 2.2, Corollary 3.3]. Now, suppose that
![]() $\dim S_{Q}(I)=d$
. Then, by Serre’s theorem [Reference Bruns and Herzog2, Theorem 4.7.10],
$\dim S_{Q}(I)=d$
. Then, by Serre’s theorem [Reference Bruns and Herzog2, Theorem 4.7.10],
and since
![]() $\unicode[STIX]{x1D712}_{1}(Q\mathbf{T},S)\geqslant 0$
, the equality in (a) holds if and only if
$\unicode[STIX]{x1D712}_{1}(Q\mathbf{T},S)\geqslant 0$
, the equality in (a) holds if and only if
![]() $Q\mathbf{T}$
yields a regular sequence on
$Q\mathbf{T}$
yields a regular sequence on
![]() $S$
. This proves the assertions (3)(a) and (3)(b). Assertion (3)(c) follows from [Reference Huckaba17, Theorem 3.1].◻
$S$
. This proves the assertions (3)(a) and (3)(b). Assertion (3)(c) follows from [Reference Huckaba17, Theorem 3.1].◻
Remark 2.2. (see [Reference Corso, Polini and Vaz Pinto6, Lemma 3.8])
We make several observations about the Sally fiber
![]() $S/(Q\mathbf{T})S$
. A crude estimation for the length of the fiber of
$S/(Q\mathbf{T})S$
. A crude estimation for the length of the fiber of
![]() $S$
is
$S$
is
![]() $\unicode[STIX]{x1D706}(S/(Q\mathbf{T})S)\geqslant r-1$
. Refinements require information about the lengths of the modules
$\unicode[STIX]{x1D706}(S/(Q\mathbf{T})S)\geqslant r-1$
. Refinements require information about the lengths of the modules
![]() $I^{n+1}/QI^{n}$
. Let us consider a very extreme case. Suppose that
$I^{n+1}/QI^{n}$
. Let us consider a very extreme case. Suppose that
![]() $I^{n+1}/QI^{n}$
is cyclic for some
$I^{n+1}/QI^{n}$
is cyclic for some
![]() $n\geqslant 1$
. Write
$n\geqslant 1$
. Write
![]() $I^{n+1}/QI^{n}\simeq \mathbf{R}/L_{n}$
, where
$I^{n+1}/QI^{n}\simeq \mathbf{R}/L_{n}$
, where
![]() $L_{n}$
is an ideal of
$L_{n}$
is an ideal of
![]() $\mathbf{R}$
. We claim that
$\mathbf{R}$
. We claim that
![]() $I^{n+2}/QI^{n+1}\simeq \mathbf{R}/L_{n+1}$
,
$I^{n+2}/QI^{n+1}\simeq \mathbf{R}/L_{n+1}$
,
![]() $L_{n}\subset L_{n+1}$
. For notational simplicity, we pick
$L_{n}\subset L_{n+1}$
. For notational simplicity, we pick
![]() $n=1$
, but the argument applies to all cases. We have
$n=1$
, but the argument applies to all cases. We have
![]() $I^{2}=(ab)+QI$
,
$I^{2}=(ab)+QI$
,
![]() $a,b\in I$
. We claim that
$a,b\in I$
. We claim that
![]() $I^{3}=(a^{2}b)+QI^{2}$
. If
$I^{3}=(a^{2}b)+QI^{2}$
. If
![]() $c,d,e\in I$
, we have
$c,d,e\in I$
, we have
![]() $cd\in (ab)+QI$
, and thus
$cd\in (ab)+QI$
, and thus
![]() $cde\in a(be)+QI^{2}\subset (a^{2}b)+QI^{2}$
. We also have
$cde\in a(be)+QI^{2}\subset (a^{2}b)+QI^{2}$
. We also have
![]() $L_{1}(a^{2}b)=aL_{1}(ab)\subset QI^{2}$
. This gives the following exact value for the length of the fiber of
$L_{1}(a^{2}b)=aL_{1}(ab)\subset QI^{2}$
. This gives the following exact value for the length of the fiber of
![]() $S$
: if
$S$
: if
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then
![]() $\unicode[STIX]{x1D706}(S/(Q\mathbf{T})S)=r-1$
.
$\unicode[STIX]{x1D706}(S/(Q\mathbf{T})S)=r-1$
.
We recall from the literature several properties of ideals
![]() $I$
such that
$I$
such that
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
.
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
.
Proposition 2.3. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
![]() $d>0$
. Let
$d>0$
. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal, and let
$\mathfrak{m}$
-primary ideal, and let
![]() $Q$
be a minimal reduction of
$Q$
be a minimal reduction of
![]() $I$
such that
$I$
such that
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
. Then, the following hold:
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
. Then, the following hold:
-
(1)
 $\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
;
$\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
; -
(2)
 $\text{depth}~\mathbf{R}[I\mathbf{T}]\geqslant d$
;
$\text{depth}~\mathbf{R}[I\mathbf{T}]\geqslant d$
; -
(3)
 $S_{Q}(I)$
is Cohen–Macaulay of dimension
$S_{Q}(I)$
is Cohen–Macaulay of dimension
 $d$
;
$d$
; -
(4)
 $\text{r}_{Q}(I)$
is independent of the choice of a minimal reduction
$\text{r}_{Q}(I)$
is independent of the choice of a minimal reduction
 $Q$
;
$Q$
; -
(5)
 $\text{r}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1>1$
;
$\text{r}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1>1$
; -
(6)
 $\text{r}(I)+1$
is a bound on the degrees of the defining equations of
$\text{r}(I)+1$
is a bound on the degrees of the defining equations of
 $\text{gr}_{I}(\mathbf{R})$
.
$\text{gr}_{I}(\mathbf{R})$
.
Proof. Assertion (1) is proved in [Reference Corso, Polini and Vaz Pinto6, Corollary 3.11]. Assertions (1) and (2) are equivalent over a Cohen–Macaulay ring of dimension
![]() $d$
. Assertion (3) follows from (2). Assertion (4) is proved in [Reference Trung26, Theorem 1.2(i)]. Assertion (5) follows from (4), Theorem 2.1 and Remark 2.2. Assertion (6) is proved in [Reference Trung26, Theorem 1.2(ii)].◻
$d$
. Assertion (3) follows from (2). Assertion (4) is proved in [Reference Trung26, Theorem 1.2(i)]. Assertion (5) follows from (4), Theorem 2.1 and Remark 2.2. Assertion (6) is proved in [Reference Trung26, Theorem 1.2(ii)].◻
The following construction leads to other classes of almost Cohen–Macaulay algebras. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d$
and depth
$d$
and depth
![]() $r$
. Let
$r$
. Let
![]() $Q$
be an ideal generated by a system of parameters that forms a proper sequence. Let us now explore the depth of the Rees algebra of
$Q$
be an ideal generated by a system of parameters that forms a proper sequence. Let us now explore the depth of the Rees algebra of
![]() $Q$
. For this we make use of the approximation complex
$Q$
. For this we make use of the approximation complex
![]() ${\mathcal{Z}}(Q)$
(see [Reference Herzog, Simis and Vasconcelos14] for details):
${\mathcal{Z}}(Q)$
(see [Reference Herzog, Simis and Vasconcelos14] for details):
where
![]() $\mathbf{B}=\mathbf{R}[T_{1},\ldots ,T_{d}]$
and the module
$\mathbf{B}=\mathbf{R}[T_{1},\ldots ,T_{d}]$
and the module
![]() $Z_{i}$
is that of the
$Z_{i}$
is that of the
![]() $i$
-cycles of the Koszul complex
$i$
-cycles of the Koszul complex
![]() $K(Q)$
.
$K(Q)$
.
To determine the depth of the coefficient modules of
![]() ${\mathcal{Z}}(Q)$
, consider the Koszul complex
${\mathcal{Z}}(Q)$
, consider the Koszul complex
![]() $K(Q)$
:
$K(Q)$
:
The subcomplex up to
![]() $K_{d-r}$
is acyclic since
$K_{d-r}$
is acyclic since
![]() $\text{depth}~\mathbf{R}=r$
. Thus, for
$\text{depth}~\mathbf{R}=r$
. Thus, for
![]() $i\geqslant d-r+1$
, the module
$i\geqslant d-r+1$
, the module
![]() $Z_{i}$
of
$Z_{i}$
of
![]() $i$
-cycles has a minimal free resolution
$i$
-cycles has a minimal free resolution
in particular,
![]() $\text{projdim}\,Z_{i}=d-1-i$
. By the Auslander–Buchsbaum equality, we have
$\text{projdim}\,Z_{i}=d-1-i$
. By the Auslander–Buchsbaum equality, we have
![]() $\text{depth}~Z_{i}=r-d+1+i$
. Thus,
$\text{depth}~Z_{i}=r-d+1+i$
. Thus,
![]() $\text{depth}~H_{0}({\mathcal{Z}})\geqslant r+1$
. In particular, if
$\text{depth}~H_{0}({\mathcal{Z}})\geqslant r+1$
. In particular, if
![]() $I$
is generated by a
$I$
is generated by a
![]() $d$
-sequence,
$d$
-sequence,
![]() $\text{depth}~\mathbf{R}[Q\mathbf{T}]=r+1$
.
$\text{depth}~\mathbf{R}[Q\mathbf{T}]=r+1$
.
Proposition 2.4. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d$
and depth
$d$
and depth
![]() $d-1$
, let
$d-1$
, let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal, and let
$\mathfrak{m}$
-primary ideal, and let
![]() $Q$
be one of its minimal reductions. Denote by
$Q$
be one of its minimal reductions. Denote by
![]() $\unicode[STIX]{x1D711}$
the matrix of syzygies of
$\unicode[STIX]{x1D711}$
the matrix of syzygies of
![]() $Q$
. Suppose that
$Q$
. Suppose that
![]() $Q$
is generated by a d-sequence and that the Sally module
$Q$
is generated by a d-sequence and that the Sally module
![]() $S_{Q}(I)$
is Cohen–Macaulay. If the first Fitting ideal
$S_{Q}(I)$
is Cohen–Macaulay. If the first Fitting ideal
![]() $I_{1}(\unicode[STIX]{x1D711})$
of
$I_{1}(\unicode[STIX]{x1D711})$
of
![]() $Q$
is contained in
$Q$
is contained in
![]() $I$
, then
$I$
, then
![]() $\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.
$\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.
Proof. We start with the exact sequence defining
![]() $S_{Q}(I)$
:
$S_{Q}(I)$
:
From the theory of the approximation complex (see [Reference Herzog, Simis and Vasconcelos14]), we have
![]() $\text{depth}~\text{gr}_{Q}(\mathbf{R})=d-1$
, while the calculation above shows that
$\text{depth}~\text{gr}_{Q}(\mathbf{R})=d-1$
, while the calculation above shows that
![]() $\text{depth}~\mathbf{R}[Q\mathbf{T}]=d$
. Since
$\text{depth}~\mathbf{R}[Q\mathbf{T}]=d$
. Since
![]() $I_{1}(\unicode[STIX]{x1D711})\subset I$
, we have that
$I_{1}(\unicode[STIX]{x1D711})\subset I$
, we have that
![]() $\mathbf{R}/I\otimes _{\mathbf{R}}\text{gr}_{Q}(\mathbf{R})=\mathbf{R}/I[\mathbf{T}_{1},\ldots ,\mathbf{T}_{d}]$
. Consider the exact sequence
$\mathbf{R}/I\otimes _{\mathbf{R}}\text{gr}_{Q}(\mathbf{R})=\mathbf{R}/I[\mathbf{T}_{1},\ldots ,\mathbf{T}_{d}]$
. Consider the exact sequence
It yields
![]() $\text{depth}~I\mathbf{R}[QT]\geqslant d$
. Since
$\text{depth}~I\mathbf{R}[QT]\geqslant d$
. Since
![]() $S_{Q}(I)$
is Cohen–Macaulay, we have
$S_{Q}(I)$
is Cohen–Macaulay, we have
![]() $\text{depth}~I\mathbf{R}[I\mathbf{T}]\geqslant d$
. Now, we make use of the tautological exact sequence
$\text{depth}~I\mathbf{R}[I\mathbf{T}]\geqslant d$
. Now, we make use of the tautological exact sequence
to get
![]() $\text{depth}~\mathbf{R}[I\mathbf{T}]\geqslant d-1$
. Finally, from
$\text{depth}~\mathbf{R}[I\mathbf{T}]\geqslant d-1$
. Finally, from
![]() $I\mathbf{T}\mathbf{R}[I\mathbf{T}]\simeq I\mathbf{R}[I\mathbf{T}][-1]$
and the exact sequence
$I\mathbf{T}\mathbf{R}[I\mathbf{T}]\simeq I\mathbf{R}[I\mathbf{T}][-1]$
and the exact sequence
we get
![]() $\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.◻
$\text{depth}~\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.◻
Corollary 2.5. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Buchsbaum local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Buchsbaum local ring of dimension
![]() $d$
and depth
$d$
and depth
![]() $d-1$
. Let
$d-1$
. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal, and let
$\mathfrak{m}$
-primary ideal, and let
![]() $Q$
be one of its minimal reductions. Denote by
$Q$
be one of its minimal reductions. Denote by
![]() $\unicode[STIX]{x1D711}$
the matrix of syzygies of
$\unicode[STIX]{x1D711}$
the matrix of syzygies of
![]() $Q$
. Suppose that the Sally module
$Q$
. Suppose that the Sally module
![]() $S_{Q}(I)$
is Cohen–Macaulay. If
$S_{Q}(I)$
is Cohen–Macaulay. If
![]() $I_{1}(\unicode[STIX]{x1D711})\subset I$
, then
$I_{1}(\unicode[STIX]{x1D711})\subset I$
, then
![]() $\text{r}(I)+1$
is a bound on the degrees of the defining equations of
$\text{r}(I)+1$
is a bound on the degrees of the defining equations of
![]() $\text{gr}_{I}(\mathbf{R})$
.
$\text{gr}_{I}(\mathbf{R})$
.
Proof. The assertion follows from Proposition 2.4 and [Reference Trung26, Theorem 1.2(ii)]. ◻
Change of rings for Sally modules
Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $\unicode[STIX]{x1D711}:\mathbf{R}\rightarrow \mathbb{S}$
be a finite homomorphism. Suppose that
$\unicode[STIX]{x1D711}:\mathbf{R}\rightarrow \mathbb{S}$
be a finite homomorphism. Suppose that
![]() $\mathbb{S}$
is a Cohen–Macaulay ring. Let
$\mathbb{S}$
is a Cohen–Macaulay ring. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary
$\mathfrak{m}$
-primary
![]() $\mathbf{R}$
-ideal with a minimal reduction
$\mathbf{R}$
-ideal with a minimal reduction
![]() $Q$
. For each maximal ideal
$Q$
. For each maximal ideal
![]() $\mathfrak{M}$
of
$\mathfrak{M}$
of
![]() $\mathbb{S}$
, the ideal
$\mathbb{S}$
, the ideal
![]() $I\mathbb{S}_{\mathfrak{M}}$
is
$I\mathbb{S}_{\mathfrak{M}}$
is
![]() $\mathfrak{M}\mathbb{S}_{\mathfrak{M}}$
-primary and
$\mathfrak{M}\mathbb{S}_{\mathfrak{M}}$
-primary and
![]() $Q\mathbb{S}_{\mathfrak{M}}$
is a minimal reduction of
$Q\mathbb{S}_{\mathfrak{M}}$
is a minimal reduction of
![]() $I\mathbb{S}_{\mathfrak{M}}$
. We define the Sally module of
$I\mathbb{S}_{\mathfrak{M}}$
. We define the Sally module of
![]() $I\mathbb{S}$
relative to
$I\mathbb{S}$
relative to
![]() $Q\mathbb{S}$
in the same manner:
$Q\mathbb{S}$
in the same manner:
Note that
![]() $S_{Q\mathbb{S}}(I\mathbb{S})$
is a finitely generated graded
$S_{Q\mathbb{S}}(I\mathbb{S})$
is a finitely generated graded
![]() $\text{gr}_{Q}(\mathbf{R})$
-module. Its localization at
$\text{gr}_{Q}(\mathbf{R})$
-module. Its localization at
![]() $\mathfrak{M}$
gives
$\mathfrak{M}$
gives
![]() $S_{Q\mathbb{S}_{\mathfrak{M}}}(I\mathbb{S}_{\mathfrak{M}})$
.
$S_{Q\mathbb{S}_{\mathfrak{M}}}(I\mathbb{S}_{\mathfrak{M}})$
.
Consider the natural mapping
![]() $\mathbf{f}_{\unicode[STIX]{x1D711}}:\mathbb{S}\otimes _{\mathbf{R}}S_{Q}(I)\rightarrow S_{Q\mathbb{S}}(I\mathbb{S})$
, which is a graded surjection. Let
$\mathbf{f}_{\unicode[STIX]{x1D711}}:\mathbb{S}\otimes _{\mathbf{R}}S_{Q}(I)\rightarrow S_{Q\mathbb{S}}(I\mathbb{S})$
, which is a graded surjection. Let
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\mathbf{R}}(\mathbb{S})$
denote the minimal number of generators of
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\mathbf{R}}(\mathbb{S})$
denote the minimal number of generators of
![]() $\mathbb{S}$
as an
$\mathbb{S}$
as an
![]() $\mathbf{R}$
-module. Combining
$\mathbf{R}$
-module. Combining
![]() $\mathbf{f}_{\unicode[STIX]{x1D711}}$
with a presentation
$\mathbf{f}_{\unicode[STIX]{x1D711}}$
with a presentation
![]() $\mathbf{R}^{\unicode[STIX]{x1D708}}\rightarrow \mathbb{S}\rightarrow 0$
gives rise to a homogeneous surjection of graded modules
$\mathbf{R}^{\unicode[STIX]{x1D708}}\rightarrow \mathbb{S}\rightarrow 0$
gives rise to a homogeneous surjection of graded modules
The following takes information from this construction into Theorem 2.1. It is a factor in our estimation of several reduction number calculations.
Theorem 2.6. (Change of Rings Theorem)
Let
![]() $\mathbf{R},\mathbb{S},I,Q$
be as above. Then,
$\mathbf{R},\mathbb{S},I,Q$
be as above. Then,
-
(1) if
 $\dim S_{Q}(I)<d$
, then
$\dim S_{Q}(I)<d$
, then
 $S_{Q\mathbb{S}}(I\mathbb{S})=0$
;
$S_{Q\mathbb{S}}(I\mathbb{S})=0$
; -
(2) if
 $\text{s}_{Q\mathbb{S}}(I\mathbb{S})\neq 0$
, then
$\text{s}_{Q\mathbb{S}}(I\mathbb{S})\neq 0$
, then
 $\dim S_{Q}(I)=d$
;
$\dim S_{Q}(I)=d$
; -
(3)
 $\text{s}_{Q\mathbb{S}}(I\mathbb{S})\leqslant \unicode[STIX]{x1D708}_{\mathbf{R}}(\mathbb{S})\cdot \text{s}_{Q}(I)$
.
$\text{s}_{Q\mathbb{S}}(I\mathbb{S})\leqslant \unicode[STIX]{x1D708}_{\mathbf{R}}(\mathbb{S})\cdot \text{s}_{Q}(I)$
.
Proof. All of the assertions follow from the surjection
![]() $\displaystyle [S_{Q}(I)]^{\unicode[STIX]{x1D708}}\rightarrow S_{Q\mathbb{S}}(I\mathbb{S})$
, where
$\displaystyle [S_{Q}(I)]^{\unicode[STIX]{x1D708}}\rightarrow S_{Q\mathbb{S}}(I\mathbb{S})$
, where
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\mathbf{R}}(\mathbb{S})$
, and the vanishing property of Sally modules over Cohen–Macaulay rings (Theorem 2.1(2)).◻
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\mathbf{R}}(\mathbb{S})$
, and the vanishing property of Sally modules over Cohen–Macaulay rings (Theorem 2.1(2)).◻
Remark 2.7. It would be good to prove that the condition 2.6(2) is actually an equivalence.
To allow a discussion of some results in Section 3, we give several observations on a technique to construct Rees algebras that are almost Cohen–Macaulay; that is, depth
![]() $\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.
$\text{gr}_{I}(\mathbf{R})\geqslant d-1$
.
We assume that
![]() $(\mathbf{R},\mathfrak{m})$
is a Gorenstein local ring and take a parameter ideal
$(\mathbf{R},\mathfrak{m})$
is a Gorenstein local ring and take a parameter ideal
![]() $Q$
. Let
$Q$
. Let
![]() $I$
be an almost complete intersection,
$I$
be an almost complete intersection,
![]() $Q\subset I$
. We look only at cases when
$Q\subset I$
. We look only at cases when
![]() $\unicode[STIX]{x1D706}(I/Q)$
is small. Recall that if
$\unicode[STIX]{x1D706}(I/Q)$
is small. Recall that if
![]() $\unicode[STIX]{x1D706}(I/Q)=1$
, then
$\unicode[STIX]{x1D706}(I/Q)=1$
, then
![]() $I^{2}=QI$
. Let us consider Northcott ideals (see [Reference Vasconcelos29, Theorem 1.113]). Let
$I^{2}=QI$
. Let us consider Northcott ideals (see [Reference Vasconcelos29, Theorem 1.113]). Let
![]() $\mathbf{R}=k[x,y]$
, and let
$\mathbf{R}=k[x,y]$
, and let
![]() $\mathfrak{m}=(x,y)$
. Let
$\mathfrak{m}=(x,y)$
. Let
![]() $Q=(a,b)$
be an
$Q=(a,b)$
be an
![]() $\mathfrak{m}$
-primary ideal of
$\mathfrak{m}$
-primary ideal of
![]() $\mathbf{R}$
. Suppose that
$\mathbf{R}$
. Suppose that
![]() $Q\subset \mathfrak{m}^{n+1}$
,
$Q\subset \mathfrak{m}^{n+1}$
,
![]() $n\geqslant 2$
, and let
$n\geqslant 2$
, and let
![]() $L=(x,y^{n})$
. Then,
$L=(x,y^{n})$
. Then,
![]() $I=Q:L=(a,b,c)$
is a proper ideal of
$I=Q:L=(a,b,c)$
is a proper ideal of
![]() $\mathbf{R}$
. Recall how
$\mathbf{R}$
. Recall how
![]() $c$
arises. Write
$c$
arises. Write
for some
![]() $a_{1},a_{2},b_{1},b_{2}$
in
$a_{1},a_{2},b_{1},b_{2}$
in
![]() $\mathbf{R}$
. Then, we have
$\mathbf{R}$
. Then, we have
![]() $c=a_{1}b_{2}-a_{2}b_{1}$
. Note that
$c=a_{1}b_{2}-a_{2}b_{1}$
. Note that
![]() $Q:c=(x,y^{n})$
. Thus,
$Q:c=(x,y^{n})$
. Thus,
![]() $\unicode[STIX]{x1D706}(I/Q)=\unicode[STIX]{x1D706}(\mathbf{R}/(x,y^{n}))=n$
.
$\unicode[STIX]{x1D706}(I/Q)=\unicode[STIX]{x1D706}(\mathbf{R}/(x,y^{n}))=n$
.
For these ideals
![]() $Q$
, we further have the following.
$Q$
, we further have the following.
Proposition 2.8. The ideal
![]() $Q:(x,y^{n})$
is integral over
$Q:(x,y^{n})$
is integral over
![]() $Q$
.
$Q$
.
Proof. To control the integrality of direct links, one can make use of [Reference Corso, Goto, Huneke, Polini and Ulrich4, Theorem 2.3], [Reference Wang30, Theorem 3.1] or [Reference Watanabe and Yoshida31, Theorem 7.4]:
in particular,
![]() $Q:\mathfrak{m}^{n}$
is integral over
$Q:\mathfrak{m}^{n}$
is integral over
![]() $Q$
. Since
$Q$
. Since
![]() $\mathfrak{m}^{n}\subset (x,y^{n})$
,
$\mathfrak{m}^{n}\subset (x,y^{n})$
,
![]() $Q:(x,y^{n})\subset Q:\mathfrak{m}^{n}$
. Thus,
$Q:(x,y^{n})\subset Q:\mathfrak{m}^{n}$
. Thus,
![]() $Q:(x,y^{n})$
is also integral over
$Q:(x,y^{n})$
is also integral over
![]() $Q$
.◻
$Q$
.◻
In this study, it is important to find the lengths of the modules
![]() $I^{n+1}/QI^{n}$
. One case that is important for us is given by the following.
$I^{n+1}/QI^{n}$
. One case that is important for us is given by the following.
Proposition 2.9. [Reference Hong, Simis and Vasconcelos15, Proposition 3.12]
Let
![]() $\mathbf{R}$
be a Gorenstein local ring. Let
$\mathbf{R}$
be a Gorenstein local ring. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal of
$\mathfrak{m}$
-primary ideal of
![]() $\mathbf{R}$
, and let
$\mathbf{R}$
, and let
![]() $Q$
be a minimal reduction of
$Q$
be a minimal reduction of
![]() $I$
. Suppose that
$I$
. Suppose that
![]() $\unicode[STIX]{x1D708}(I/Q)=1$
. Then,
$\unicode[STIX]{x1D708}(I/Q)=1$
. Then,
where
![]() $\unicode[STIX]{x1D711}$
is the matrix of syzygies of
$\unicode[STIX]{x1D711}$
is the matrix of syzygies of
![]() $I$
.
$I$
.
Example 2.10. Let us consider some examples. In the case of the Northcott ideals above, we have
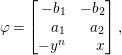 $$\begin{eqnarray}\unicode[STIX]{x1D711}=\left[\begin{array}{@{}rr@{}}-b_{1} & -b_{2}\\ a_{1} & a_{2}\\ -y^{n} & x\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}=\left[\begin{array}{@{}rr@{}}-b_{1} & -b_{2}\\ a_{1} & a_{2}\\ -y^{n} & x\end{array}\right],\end{eqnarray}$$
![]() $I_{1}(\unicode[STIX]{x1D711})=(x,y^{n},a_{1},a_{2},b_{1},b_{2})=(x,y^{m})$
, where
$I_{1}(\unicode[STIX]{x1D711})=(x,y^{n},a_{1},a_{2},b_{1},b_{2})=(x,y^{m})$
, where
![]() $1\leqslant m\leqslant n$
. Appropriate choices for
$1\leqslant m\leqslant n$
. Appropriate choices for
![]() $a_{2}$
or
$a_{2}$
or
![]() $b_{2}$
give rise to all values for
$b_{2}$
give rise to all values for
![]() $m$
in the range. For example, let
$m$
in the range. For example, let
![]() $Q=(x^{4}+y^{5},x^{2}y^{2}+xy^{3})$
, let
$Q=(x^{4}+y^{5},x^{2}y^{2}+xy^{3})$
, let
![]() $L=(x,y^{3})$
, and let
$L=(x,y^{3})$
, and let
![]() $I=Q:L$
. Then,
$I=Q:L$
. Then,
![]() $\unicode[STIX]{x1D706}(I/Q)=3$
and
$\unicode[STIX]{x1D706}(I/Q)=3$
and
![]() $I_{1}(\unicode[STIX]{x1D711})=(x,y^{2})$
. Hence, by Proposition 2.9,
$I_{1}(\unicode[STIX]{x1D711})=(x,y^{2})$
. Hence, by Proposition 2.9,
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
. In fact, the reduction number
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
. In fact, the reduction number
![]() $r_{Q}(I)=2$
. More generally, choosing
$r_{Q}(I)=2$
. More generally, choosing
![]() $m=n-1$
above gives
$m=n-1$
above gives
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, by Proposition 2.9. Moreover, if
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, by Proposition 2.9. Moreover, if
![]() $(a_{1},a_{2},b_{1},b_{2})\subset (x,y^{n})$
, then
$(a_{1},a_{2},b_{1},b_{2})\subset (x,y^{n})$
, then
![]() $I^{2}=QI$
, by Proposition 2.9.
$I^{2}=QI$
, by Proposition 2.9.
3 Almost complete intersections
This section makes use of the behavior of the components of Sally modules of almost complete intersections in order to derive uniform bounds for reduction numbers. We begin with the following result.
Proposition 3.1. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d$
with infinite residue field, and let
$d$
with infinite residue field, and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary almost complete intersection ideal with a minimal reduction
$\mathfrak{m}$
-primary almost complete intersection ideal with a minimal reduction
![]() $Q$
. If for some integer
$Q$
. If for some integer
![]() $n$
,
$n$
,
![]() $\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
, then
$\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
, then
![]() $\text{r}(I)\leqslant n\unicode[STIX]{x1D708}(\mathfrak{m})-1$
.
$\text{r}(I)\leqslant n\unicode[STIX]{x1D708}(\mathfrak{m})-1$
.
Proof. Since
![]() $Q$
is a minimal reduction of
$Q$
is a minimal reduction of
![]() $I$
, it is generated by a subset of the minimal set of generators of
$I$
, it is generated by a subset of the minimal set of generators of
![]() $I$
; that is,
$I$
; that is,
![]() $I=(Q,a)$
. The expected number of generators of
$I=(Q,a)$
. The expected number of generators of
![]() $I^{n}$
is
$I^{n}$
is
![]() $\binom{d+n}{n}$
. A lesser value for
$\binom{d+n}{n}$
. A lesser value for
![]() $\unicode[STIX]{x1D708}(I^{n})$
would imply by [Reference Eakin and Sathaye7, Theorem 1] that
$\unicode[STIX]{x1D708}(I^{n})$
would imply by [Reference Eakin and Sathaye7, Theorem 1] that
![]() $I^{n}=JI^{n-1}$
for some minimal reduction
$I^{n}=JI^{n-1}$
for some minimal reduction
![]() $J$
of
$J$
of
![]() $I$
, and therefore
$I$
, and therefore
![]() $\text{r}(I)\leqslant n-1$
.
$\text{r}(I)\leqslant n-1$
.
Suppose that
![]() $\unicode[STIX]{x1D708}(I^{n})=\binom{d+n}{n}$
. Since
$\unicode[STIX]{x1D708}(I^{n})=\binom{d+n}{n}$
. Since
![]() $\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
,
$\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
,
![]() $\mathfrak{m}I^{n}\subset QI^{n-1}$
. Moreover, we have
$\mathfrak{m}I^{n}\subset QI^{n-1}$
. Moreover, we have
Note that
It follows that
![]() $\mathfrak{m}I^{n}=\mathfrak{m}QI^{n-1}$
. From the Cayley–Hamilton theorem, we have
$\mathfrak{m}I^{n}=\mathfrak{m}QI^{n-1}$
. From the Cayley–Hamilton theorem, we have
![]() $(I^{n})^{s}=(QI^{n-1})(I^{n})^{s-1}$
, where
$(I^{n})^{s}=(QI^{n-1})(I^{n})^{s-1}$
, where
![]() $s=\unicode[STIX]{x1D708}(\mathfrak{m})$
. In particular,
$s=\unicode[STIX]{x1D708}(\mathfrak{m})$
. In particular,
![]() $I^{ns}=QI^{ns-1}$
, as desired. ◻
$I^{ns}=QI^{ns-1}$
, as desired. ◻
Next, we give examples of ideals with
![]() $\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
for some integer
$\unicode[STIX]{x1D706}(I^{n}/QI^{n-1})=1$
for some integer
![]() $n$
.
$n$
.
Example 3.2. Let
![]() $\mathbf{R}=k[x,y]$
, where
$\mathbf{R}=k[x,y]$
, where
![]() $k$
is an infinite field,
$k$
is an infinite field,
![]() $Q=(x^{6}+y^{5},x^{7}+x^{5}y)$
, and consider the ideals
$Q=(x^{6}+y^{5},x^{7}+x^{5}y)$
, and consider the ideals
![]() $Q:L$
, where
$Q:L$
, where
![]() $L=(x,y^{n})$
for some positive integer
$L=(x,y^{n})$
for some positive integer
![]() $n$
.
$n$
.
-
(1) If
 $I=Q:(x,y^{2})$
, then
$I=Q:(x,y^{2})$
, then
 $I^{2}=QI$
.
$I^{2}=QI$
. -
(2) If
 $I=Q:(x,y^{3})$
, then
$I=Q:(x,y^{3})$
, then
 $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
,
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
,
 $\text{r}(I)=2$
.
$\text{r}(I)=2$
. -
(3) If
 $I=Q:(x,y^{4})$
, then
$I=Q:(x,y^{4})$
, then
 $\unicode[STIX]{x1D706}(I^{2}/QI)=3$
,
$\unicode[STIX]{x1D706}(I^{2}/QI)=3$
,
 $\unicode[STIX]{x1D706}(I^{3}/QI^{2})=2$
,
$\unicode[STIX]{x1D706}(I^{3}/QI^{2})=2$
,
 $\unicode[STIX]{x1D706}(I^{4}/QI^{3})=1$
,
$\unicode[STIX]{x1D706}(I^{4}/QI^{3})=1$
,
 $\text{r}(I)=5$
.
$\text{r}(I)=5$
. -
(4)
 $I=Q:(x,y^{5})=(x^{6}+x^{4}y,y^{5}-x^{4}y)$
is a complete intersection. Notice that
$I=Q:(x,y^{5})=(x^{6}+x^{4}y,y^{5}-x^{4}y)$
is a complete intersection. Notice that
 $I$
is not integral over
$I$
is not integral over
 $Q$
(see Proposition 2.8).
$Q$
(see Proposition 2.8).
Corollary 3.3. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Gorenstein local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Gorenstein local ring of dimension
![]() $d$
with infinite residue field, and let
$d$
with infinite residue field, and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal with a minimal reduction
$\mathfrak{m}$
-primary ideal with a minimal reduction
![]() $Q$
. If
$Q$
. If
![]() $\unicode[STIX]{x1D706}(I/Q)=2$
, then
$\unicode[STIX]{x1D706}(I/Q)=2$
, then
![]() $\text{r}(I)\leqslant 2\unicode[STIX]{x1D708}(\mathfrak{m})-1$
.
$\text{r}(I)\leqslant 2\unicode[STIX]{x1D708}(\mathfrak{m})-1$
.
Proof. According to Proposition 2.9, since
![]() $\unicode[STIX]{x1D706}(I/Q)=2$
, we have that
$\unicode[STIX]{x1D706}(I/Q)=2$
, we have that
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
.◻
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
.◻
Corollary 3.4. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
![]() $d$
with infinite residue field, and let
$d$
with infinite residue field, and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary almost complete intersection ideal with a minimal reduction
$\mathfrak{m}$
-primary almost complete intersection ideal with a minimal reduction
![]() $Q$
. If
$Q$
. If
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then
![]() $\mathfrak{m}I^{n}=\mathfrak{m}IQ^{n-1}$
for
$\mathfrak{m}I^{n}=\mathfrak{m}IQ^{n-1}$
for
![]() $n\geqslant 2$
. In particular,
$n\geqslant 2$
. In particular,
![]() $\mathfrak{m}S_{Q}(I)=0$
.
$\mathfrak{m}S_{Q}(I)=0$
.
Proof. Recall that
![]() $\text{r}(I)>1$
, by Proposition 2.3(5). Then, from the proof of Proposition 3.1, we have that
$\text{r}(I)>1$
, by Proposition 2.3(5). Then, from the proof of Proposition 3.1, we have that
![]() $\mathfrak{m}I^{2}=\mathfrak{m}QI$
. If
$\mathfrak{m}I^{2}=\mathfrak{m}QI$
. If
![]() $n>2$
, it follows that
$n>2$
, it follows that
as desired. ◻
Following [Reference Corso, Polini and Vasconcelos5], we study relationships between
![]() $\text{r}(I)$
and the multiplicity
$\text{r}(I)$
and the multiplicity
![]() $f_{0}(I)$
of the special fiber
$f_{0}(I)$
of the special fiber
![]() ${\mathcal{F}}(I)=\mathbf{R}[I\mathbf{T}]\otimes \mathbf{R}/\mathfrak{m}$
of the Rees algebra of
${\mathcal{F}}(I)=\mathbf{R}[I\mathbf{T}]\otimes \mathbf{R}/\mathfrak{m}$
of the Rees algebra of
![]() $I$
.
$I$
.
Proposition 3.5. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal that is an almost complete intersection. Let
$\mathfrak{m}$
-primary ideal that is an almost complete intersection. Let
![]() $Q$
be a minimal reduction of
$Q$
be a minimal reduction of
![]() $I$
, and let
$I$
, and let
![]() $S_{Q}(I)$
denote the Sally module of
$S_{Q}(I)$
denote the Sally module of
![]() $I$
relative to
$I$
relative to
![]() $Q$
. Setting
$Q$
. Setting
![]() $\mathbf{A}={\mathcal{F}}(Q)$
, there is an exact sequence
$\mathbf{A}={\mathcal{F}}(Q)$
, there is an exact sequence
Proof. Let
![]() $I=(Q,a)$
. Consider the exact sequence introduced in [Reference Corso, Polini and Vasconcelos5, Proof of 2.1]:
$I=(Q,a)$
. Consider the exact sequence introduced in [Reference Corso, Polini and Vasconcelos5, Proof of 2.1]:
where
![]() $\unicode[STIX]{x1D711}$
is the map defined by
$\unicode[STIX]{x1D711}$
is the map defined by
![]() $\unicode[STIX]{x1D711}(f,g)=f+ag\mathbf{T}$
. Tensoring this sequence with
$\unicode[STIX]{x1D711}(f,g)=f+ag\mathbf{T}$
. Tensoring this sequence with
![]() $\mathbf{R}/\mathfrak{m}$
yields the desired sequence and the induced map
$\mathbf{R}/\mathfrak{m}$
yields the desired sequence and the induced map
![]() $\overline{\unicode[STIX]{x1D711}}$
.◻
$\overline{\unicode[STIX]{x1D711}}$
.◻
Corollary 3.6. In the set up of Proposition 3.5, suppose that
![]() $\mathbf{R}$
has infinite residue field and that
$\mathbf{R}$
has infinite residue field and that
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
. Then,
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
. Then,
-
(1)
 $\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1\leqslant f_{0}(I)\leqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2=\text{r}(I)+1$
;
$\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1\leqslant f_{0}(I)\leqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2=\text{r}(I)+1$
; -
(2)
 ${\mathcal{F}}(I)$
is Cohen–Macaulay if and only if
${\mathcal{F}}(I)$
is Cohen–Macaulay if and only if
 $f_{0}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
.
$f_{0}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
.
Proof. First, we notice that
![]() $\mathfrak{m}S_{Q}(I)=0$
by Corollary 3.4, so that
$\mathfrak{m}S_{Q}(I)=0$
by Corollary 3.4, so that
![]() $S_{Q}(I)\otimes \mathbf{R}/\mathfrak{m}\simeq S_{Q}(I)$
. Then,
$S_{Q}(I)\otimes \mathbf{R}/\mathfrak{m}\simeq S_{Q}(I)$
. Then,
![]() $\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1\leqslant f_{0}(I)$
follows because
$\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1\leqslant f_{0}(I)$
follows because
![]() $\mathbf{A}$
must embed in
$\mathbf{A}$
must embed in
![]() ${\mathcal{F}}(I)$
(see, for example, [Reference Huneke and Swanson19, Corollary 8.3.5]), and the cokernel of this embedding has multiplicity greater than or equal to the multiplicity of
${\mathcal{F}}(I)$
(see, for example, [Reference Huneke and Swanson19, Corollary 8.3.5]), and the cokernel of this embedding has multiplicity greater than or equal to the multiplicity of
![]() $S_{Q}(I)$
, which is
$S_{Q}(I)$
, which is
![]() $\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)$
. The inequality
$\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)$
. The inequality
![]() $f_{0}(I)\leqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
follows by reading multiplicities in the exact sequence (1), as in [Reference Corso, Polini and Vasconcelos5, Proof of 2.1]. The last equality follows from Proposition 2.3(5).
$f_{0}(I)\leqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
follows by reading multiplicities in the exact sequence (1), as in [Reference Corso, Polini and Vasconcelos5, Proof of 2.1]. The last equality follows from Proposition 2.3(5).
Now, assume that
![]() ${\mathcal{F}}(I)$
is Cohen–Macaulay. Since
${\mathcal{F}}(I)$
is Cohen–Macaulay. Since
![]() $I$
is an almost complete intersection, we have that
$I$
is an almost complete intersection, we have that
![]() ${\mathcal{F}}(I)$
is a finite extension of
${\mathcal{F}}(I)$
is a finite extension of
![]() $\mathbf{A}$
with a presentation
$\mathbf{A}$
with a presentation
![]() $\mathbf{A}[z]/L$
, where
$\mathbf{A}[z]/L$
, where
![]() $L$
has codimension 1. Since
$L$
has codimension 1. Since
![]() $\mathbf{A}[z]$
is factorial and
$\mathbf{A}[z]$
is factorial and
![]() $L$
is unmixed, it follows that
$L$
is unmixed, it follows that
![]() $L$
is principal. Write
$L$
is principal. Write
![]() $L=(h(z))$
. Note that
$L=(h(z))$
. Note that
![]() $h(z)$
must be monic and its degree is
$h(z)$
must be monic and its degree is
![]() $f_{0}(I)=\text{r}(I)+1$
. Now, the conclusion follows from part (1).
$f_{0}(I)=\text{r}(I)+1$
. Now, the conclusion follows from part (1).
Conversely, the equality
![]() $f_{0}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
implies that
$f_{0}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+2$
implies that
![]() $\overline{\unicode[STIX]{x1D711}}$
is injective. Since
$\overline{\unicode[STIX]{x1D711}}$
is injective. Since
![]() $S_{Q}(I)$
is Cohen–Macaulay by Proposition 2.3(3), we have that
$S_{Q}(I)$
is Cohen–Macaulay by Proposition 2.3(3), we have that
![]() ${\mathcal{F}}(I)$
is Cohen–Macaulay.◻
${\mathcal{F}}(I)$
is Cohen–Macaulay.◻
We are now ready for one of our main results.
Theorem 3.7. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
![]() $d\geqslant 1$
with infinite residue field, and let
$d\geqslant 1$
with infinite residue field, and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal which is an almost complete intersection. If for some minimal reduction
$\mathfrak{m}$
-primary ideal which is an almost complete intersection. If for some minimal reduction
![]() $Q$
of
$Q$
of
![]() $I$
,
$I$
,
![]() $\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then the special fiber ring
$\unicode[STIX]{x1D706}(I^{2}/QI)=1$
, then the special fiber ring
![]() ${\mathcal{F}}(I)$
is Cohen–Macaulay. In particular,
${\mathcal{F}}(I)$
is Cohen–Macaulay. In particular,
![]() $\text{r}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1=f_{0}(I)-1$
.
$\text{r}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1=f_{0}(I)-1$
.
Proof. The Cohen–Macaulayness of
![]() ${\mathcal{F}}(I)$
follows once we show that the map
${\mathcal{F}}(I)$
follows once we show that the map
![]() $\overline{\unicode[STIX]{x1D711}}$
in sequence (1) is injective. To prove that
$\overline{\unicode[STIX]{x1D711}}$
in sequence (1) is injective. To prove that
![]() $\overline{\unicode[STIX]{x1D711}}$
is an embedding, we must show that its image
$\overline{\unicode[STIX]{x1D711}}$
is an embedding, we must show that its image
![]() $C$
has multiplicity
$C$
has multiplicity
![]() $2$
. Since
$2$
. Since
we have that the cokernel
![]() $D$
of the embedding
$D$
of the embedding
![]() $\mathbf{A}{\hookrightarrow}C$
is
$\mathbf{A}{\hookrightarrow}C$
is
We examine its Hilbert function,
![]() $\unicode[STIX]{x1D706}((IQ^{n-1}+\mathfrak{m}I^{n})/(Q^{n}+\mathfrak{m}I^{n}))$
, for
$\unicode[STIX]{x1D706}((IQ^{n-1}+\mathfrak{m}I^{n})/(Q^{n}+\mathfrak{m}I^{n}))$
, for
![]() $n\gg 0$
. Since
$n\gg 0$
. Since
![]() $\mathfrak{m}I^{n}=\mathfrak{m}Q^{n-1}I$
by Corollary 3.4, we have
$\mathfrak{m}I^{n}=\mathfrak{m}Q^{n-1}I$
by Corollary 3.4, we have
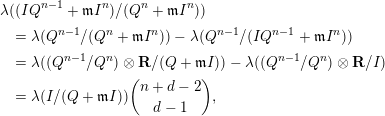 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D706}((IQ^{n-1}+\mathfrak{m}I^{n})/(Q^{n}+\mathfrak{m}I^{n}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}(Q^{n-1}/(Q^{n}+\mathfrak{m}I^{n}))-\unicode[STIX]{x1D706}(Q^{n-1}/(IQ^{n-1}+\mathfrak{m}I^{n}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}((Q^{n-1}/Q^{n})\otimes \mathbf{R}/(Q+\mathfrak{m}I))-\unicode[STIX]{x1D706}((Q^{n-1}/Q^{n})\otimes \mathbf{R}/I)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}(I/(Q+\mathfrak{m}I))\binom{n+d-2}{d-1},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D706}((IQ^{n-1}+\mathfrak{m}I^{n})/(Q^{n}+\mathfrak{m}I^{n}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}(Q^{n-1}/(Q^{n}+\mathfrak{m}I^{n}))-\unicode[STIX]{x1D706}(Q^{n-1}/(IQ^{n-1}+\mathfrak{m}I^{n}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}((Q^{n-1}/Q^{n})\otimes \mathbf{R}/(Q+\mathfrak{m}I))-\unicode[STIX]{x1D706}((Q^{n-1}/Q^{n})\otimes \mathbf{R}/I)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}(I/(Q+\mathfrak{m}I))\binom{n+d-2}{d-1},\nonumber\end{eqnarray}$$
which shows that
![]() $D$
has dimension
$D$
has dimension
![]() $d$
and multiplicity
$d$
and multiplicity
![]() $\unicode[STIX]{x1D706}(I/(Q+\mathfrak{m}I))=1$
. This concludes the proof. The last assertion follows from Corollary 3.6.◻
$\unicode[STIX]{x1D706}(I/(Q+\mathfrak{m}I))=1$
. This concludes the proof. The last assertion follows from Corollary 3.6.◻
4 Buchsbaum rings
The formula of Theorem 1.1,
![]() $\text{s}_{Q}(I)+1=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1\geqslant \text{r}_{Q}(I)$
, suggests several questions. Does it hold in higher dimensions? If
$\text{s}_{Q}(I)+1=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+1\geqslant \text{r}_{Q}(I)$
, suggests several questions. Does it hold in higher dimensions? If
![]() $\mathbf{R}$
is not Cohen–Macaulay but still
$\mathbf{R}$
is not Cohen–Macaulay but still
![]() $\dim \mathbf{R}=2$
, what is a possible bound? We aim at exploring bounds of the form
$\dim \mathbf{R}=2$
, what is a possible bound? We aim at exploring bounds of the form
We study this issue for Buchsbaum rings, where the natural Cohen–Macaulay deficiency is
![]() $I(\mathbf{R})$
, the Buchsbaum invariant of
$I(\mathbf{R})$
, the Buchsbaum invariant of
![]() $\mathbf{R}$
(see [Reference Stückrad and Vogel25, Chapter 1, Theorem 1.12]). We recall that
$\mathbf{R}$
(see [Reference Stückrad and Vogel25, Chapter 1, Theorem 1.12]). We recall that
![]() $I(\mathbf{R})=\sum _{i=0}^{d-1}\binom{d-1}{i}\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{i}(\mathbf{R}))$
, or
$I(\mathbf{R})=\sum _{i=0}^{d-1}\binom{d-1}{i}\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{i}(\mathbf{R}))$
, or
![]() $I(\mathbf{R})=\sum _{i=1}^{d}(-1)^{i}\text{e}_{i}(Q)$
(see [Reference Stückrad and Vogel25, Chapter 1, Propositions 2.6, 2.7]).
$I(\mathbf{R})=\sum _{i=1}^{d}(-1)^{i}\text{e}_{i}(Q)$
(see [Reference Stückrad and Vogel25, Chapter 1, Propositions 2.6, 2.7]).
 $S_{2}$
-fication of generalized Cohen–Macaulay rings
$S_{2}$
-fication of generalized Cohen–Macaulay rings
If
![]() $\mathbf{R}$
is a Noetherian ring with total ring of fractions
$\mathbf{R}$
is a Noetherian ring with total ring of fractions
![]() $K$
, the smallest finite extension
$K$
, the smallest finite extension
![]() $\unicode[STIX]{x1D711}:\mathbf{R}\rightarrow \mathbb{S}\subset K$
with the
$\unicode[STIX]{x1D711}:\mathbf{R}\rightarrow \mathbb{S}\subset K$
with the
![]() $S_{2}$
property is called the
$S_{2}$
property is called the
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
(see [Reference Vasconcelos29, Definition 6.20]). We refer to either
$\mathbf{R}$
(see [Reference Vasconcelos29, Definition 6.20]). We refer to either
![]() $\unicode[STIX]{x1D711}$
or
$\unicode[STIX]{x1D711}$
or
![]() $\mathbb{S}$
as the
$\mathbb{S}$
as the
![]() $S_{2}$
-ficaton of
$S_{2}$
-ficaton of
![]() $\mathbf{R}$
. Let
$\mathbf{R}$
. Let
![]() $\mathbf{R}$
be a generalized Cohen–Macaulay local ring of dimension
$\mathbf{R}$
be a generalized Cohen–Macaulay local ring of dimension
![]() $d\geqslant 2$
and positive depth. Suppose that
$d\geqslant 2$
and positive depth. Suppose that
![]() $\mathbf{R}$
has a canonical module
$\mathbf{R}$
has a canonical module
![]() $\unicode[STIX]{x1D714}_{\mathbf{R}}$
. Then, the natural morphism
$\unicode[STIX]{x1D714}_{\mathbf{R}}$
. Then, the natural morphism
is an
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
(see [Reference Aoyama1, Theorem 3.2]). Note that
$\mathbf{R}$
(see [Reference Aoyama1, Theorem 3.2]). Note that
![]() $\text{ker}(\unicode[STIX]{x1D711})=\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
(see [Reference Aoyama1, 1.11], [Reference Stückrad and Vogel25, Chapter 1, Lemma 2.2]). Let us describe some elementary properties of
$\text{ker}(\unicode[STIX]{x1D711})=\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
(see [Reference Aoyama1, 1.11], [Reference Stückrad and Vogel25, Chapter 1, Lemma 2.2]). Let us describe some elementary properties of
![]() $\mathbb{S}$
.
$\mathbb{S}$
.
Proposition 4.1. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a generalized Cohen–Macaulay local ring of dimension at least
$(\mathbf{R},\mathfrak{m})$
be a generalized Cohen–Macaulay local ring of dimension at least
![]() $2$
and of positive depth. Suppose that
$2$
and of positive depth. Suppose that
![]() $\mathbf{R}$
has a canonical module
$\mathbf{R}$
has a canonical module
![]() $\unicode[STIX]{x1D714}_{\mathbf{R}}$
, and let
$\unicode[STIX]{x1D714}_{\mathbf{R}}$
, and let
![]() $\mathbb{S}=\text{Hom}_{\mathbf{R}}(\unicode[STIX]{x1D714}_{\mathbf{R}},\unicode[STIX]{x1D714}_{\mathbf{R}})$
.
$\mathbb{S}=\text{Hom}_{\mathbf{R}}(\unicode[STIX]{x1D714}_{\mathbf{R}},\unicode[STIX]{x1D714}_{\mathbf{R}})$
.
-
(1) If
 $\mathfrak{a}=\text{ann}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
, then
$\mathfrak{a}=\text{ann}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
, then
 $\mathfrak{a}\mathbb{S}=\mathfrak{a}$
.
$\mathfrak{a}\mathbb{S}=\mathfrak{a}$
. -
(2)
 $\mathbb{S}$
is a semi-local ring.
$\mathbb{S}$
is a semi-local ring. -
(3)
 $\unicode[STIX]{x1D706}(\mathbb{S}/\mathfrak{m}\mathbb{S})=1+\unicode[STIX]{x1D708}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))\leqslant 1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
.
$\unicode[STIX]{x1D706}(\mathbb{S}/\mathfrak{m}\mathbb{S})=1+\unicode[STIX]{x1D708}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))\leqslant 1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
.
Proof. Consider the exact sequence
Note that
![]() $D\simeq \text{H}_{\mathfrak{m}}^{1}(\mathbf{R})$
is a module of finite length. From
$D\simeq \text{H}_{\mathfrak{m}}^{1}(\mathbf{R})$
is a module of finite length. From
![]() $\mathfrak{a}\mathbb{S}\subset \mathbf{R}$
, we have
$\mathfrak{a}\mathbb{S}\subset \mathbf{R}$
, we have
![]() $\mathfrak{a}\mathbb{S}\cdot \mathbb{S}\subset \mathbf{R}$
, so that
$\mathfrak{a}\mathbb{S}\cdot \mathbb{S}\subset \mathbf{R}$
, so that
![]() $\mathfrak{a}\mathbb{S}\subset \mathfrak{a}$
. On the other hand, by Nakayama’s lemma,
$\mathfrak{a}\mathbb{S}\subset \mathfrak{a}$
. On the other hand, by Nakayama’s lemma,
![]() $\mathfrak{m}\mathbb{S}$
is contained in the Jacobson radical of
$\mathfrak{m}\mathbb{S}$
is contained in the Jacobson radical of
![]() $\mathbb{S}$
. Therefore,
$\mathbb{S}$
. Therefore,
![]() $\mathbb{S}$
is semi-local. The remaining assertion is clear.◻
$\mathbb{S}$
is semi-local. The remaining assertion is clear.◻
Now, we give an explicit description of the
![]() $S_{2}$
-fication of these rings.
$S_{2}$
-fication of these rings.
Theorem 4.2. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a generalized Cohen–Macaulay local ring of dimension at least
$(\mathbf{R},\mathfrak{m})$
be a generalized Cohen–Macaulay local ring of dimension at least
![]() $2$
and positive depth. Let
$2$
and positive depth. Let
![]() $\mathfrak{a}=\text{ann}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
. Then,
$\mathfrak{a}=\text{ann}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
. Then,
![]() $\text{Hom}_{\mathbf{R}}(\mathfrak{a},\mathfrak{a})$
is an
$\text{Hom}_{\mathbf{R}}(\mathfrak{a},\mathfrak{a})$
is an
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
. Moreover, if
$\mathbf{R}$
. Moreover, if
![]() $\mathbf{R}$
is a Buchsbaum ring, then
$\mathbf{R}$
is a Buchsbaum ring, then
![]() $\text{Hom}_{\mathbf{R}}(\mathfrak{m},\mathfrak{m})$
is an
$\text{Hom}_{\mathbf{R}}(\mathfrak{m},\mathfrak{m})$
is an
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
.
$\mathbf{R}$
.
Proof. We denote
![]() $\text{Hom}_{\mathbf{R}}(\mathfrak{a},\mathfrak{a})$
by
$\text{Hom}_{\mathbf{R}}(\mathfrak{a},\mathfrak{a})$
by
![]() $E$
. Then, there is a natural morphism
$E$
. Then, there is a natural morphism
![]() $\unicode[STIX]{x1D711}:\mathbf{R}{\hookrightarrow}E$
, which is an isomorphism at each localization at
$\unicode[STIX]{x1D711}:\mathbf{R}{\hookrightarrow}E$
, which is an isomorphism at each localization at
![]() $\mathfrak{p}\neq \mathfrak{m}$
. We must show that
$\mathfrak{p}\neq \mathfrak{m}$
. We must show that
![]() $E$
satisfies
$E$
satisfies
![]() $(S_{2})$
. It suffices to show that
$(S_{2})$
. It suffices to show that
![]() $\text{grade}(\mathfrak{m})$
relative to
$\text{grade}(\mathfrak{m})$
relative to
![]() $E$
is at least
$E$
is at least
![]() $2$
.
$2$
.
To see this, we pass to the completion
![]() $\widehat{\mathbf{R}}$
of
$\widehat{\mathbf{R}}$
of
![]() $\mathbf{R}$
and show that
$\mathbf{R}$
and show that
![]() $\text{grade}(\widehat{\mathfrak{m}})$
relative to
$\text{grade}(\widehat{\mathfrak{m}})$
relative to
![]() $\widehat{E}$
is at least
$\widehat{E}$
is at least
![]() $2$
. Since
$2$
. Since
![]() $\widehat{\mathbf{R}}$
has a canonical module
$\widehat{\mathbf{R}}$
has a canonical module
![]() $\unicode[STIX]{x1D714}$
, let
$\unicode[STIX]{x1D714}$
, let
![]() $\mathbb{S}=\text{Hom}_{\widehat{\mathbf{R}}}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D714})$
be the
$\mathbb{S}=\text{Hom}_{\widehat{\mathbf{R}}}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D714})$
be the
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\widehat{\mathbf{R}}$
. Now, we identify
$\widehat{\mathbf{R}}$
. Now, we identify
![]() $\mathbb{S}$
to a subring of the total ring of fractions of
$\mathbb{S}$
to a subring of the total ring of fractions of
![]() $\widehat{\mathbf{R}}$
. By flatness,
$\widehat{\mathbf{R}}$
. By flatness,
![]() $\text{ann}(\mathbb{S}/\widehat{\mathbf{R}})=\widehat{\mathfrak{a}}$
, and by Proposition 4.1, we have
$\text{ann}(\mathbb{S}/\widehat{\mathbf{R}})=\widehat{\mathfrak{a}}$
, and by Proposition 4.1, we have
![]() $\widehat{\mathfrak{a}}\mathbb{S}=\widehat{\mathfrak{a}}$
. Thus,
$\widehat{\mathfrak{a}}\mathbb{S}=\widehat{\mathfrak{a}}$
. Thus,
The last equality is because
![]() $\widehat{\mathfrak{a}}$
is an ideal of grade at least 2 of the ring
$\widehat{\mathfrak{a}}$
is an ideal of grade at least 2 of the ring
![]() $\mathbb{S}$
.◻
$\mathbb{S}$
.◻
The Rossi index for Buchsbaum rings
The next result is an extension of Theorem 1.1 to Buchsbaum rings. We denote by
![]() $\text{s}_{Q}(I)$
the multiplicity of the Sally module of
$\text{s}_{Q}(I)$
the multiplicity of the Sally module of
![]() $I$
relative to
$I$
relative to
![]() $Q$
.
$Q$
.
Theorem 4.3. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a two-dimensional Buchsbaum local ring of positive depth. Let
$(\mathbf{R},\mathfrak{m})$
be a two-dimensional Buchsbaum local ring of positive depth. Let
![]() $\mathbb{S}$
be the
$\mathbb{S}$
be the
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
. Let
$\mathbf{R}$
. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal with a minimal reduction
$\mathfrak{m}$
-primary ideal with a minimal reduction
![]() $Q$
.
$Q$
.
-
(1) If
 $I=I\mathbb{S}$
, then
$I=I\mathbb{S}$
, then
 $\text{s}_{Q}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)-\text{e}_{1}(Q)$
and
$\text{s}_{Q}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)-\text{e}_{1}(Q)$
and
 $\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1$
.
$\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1$
. -
(2) If
 $I\subsetneq I\mathbb{S}$
, then
$I\subsetneq I\mathbb{S}$
, then
 $\text{r}_{Q}(I)\leqslant (1-\text{e}_{1}(Q))^{2}\text{s}_{Q}(I)-2\text{e}_{1}(Q)+1$
.
$\text{r}_{Q}(I)\leqslant (1-\text{e}_{1}(Q))^{2}\text{s}_{Q}(I)-2\text{e}_{1}(Q)+1$
.
Proof. We may assume that
![]() $\mathbf{R}$
is complete (see [Reference Stückrad and Vogel25, Chapter 1, Lemma 1.13]). Let
$\mathbf{R}$
is complete (see [Reference Stückrad and Vogel25, Chapter 1, Lemma 1.13]). Let
![]() $\{\mathfrak{M}_{1},\ldots ,\mathfrak{M}_{t}\}$
be the maximal ideals of
$\{\mathfrak{M}_{1},\ldots ,\mathfrak{M}_{t}\}$
be the maximal ideals of
![]() $\mathbb{S}$
, and denote by
$\mathbb{S}$
, and denote by
![]() $\mathbb{S}_{1},\ldots ,\mathbb{S}_{t}$
the corresponding localizations. For each
$\mathbb{S}_{1},\ldots ,\mathbb{S}_{t}$
the corresponding localizations. For each
![]() $i=1,\ldots ,t$
, let
$i=1,\ldots ,t$
, let
![]() $f_{i}$
be the relative degree
$f_{i}$
be the relative degree
![]() $[\mathbb{S}/\mathfrak{M}_{i}:\mathbf{R}/\mathfrak{m}]$
. If
$[\mathbb{S}/\mathfrak{M}_{i}:\mathbf{R}/\mathfrak{m}]$
. If
![]() $V$
is an
$V$
is an
![]() $\mathbf{R}$
-module of finite length which is also an
$\mathbf{R}$
-module of finite length which is also an
![]() $\mathbb{S}$
-module, then we have that
$\mathbb{S}$
-module, then we have that
Applying this formula to the modules
![]() $I^{n}\mathbb{S}/I^{n+1}\mathbb{S}$
,
$I^{n}\mathbb{S}/I^{n+1}\mathbb{S}$
,
![]() $I^{n+1}\mathbb{S}/IQ^{n}\mathbb{S}$
, for
$I^{n+1}\mathbb{S}/IQ^{n}\mathbb{S}$
, for
![]() $n\gg 0$
, and
$n\gg 0$
, and
![]() $\mathbb{S}/I\mathbb{S}$
, we get
$\mathbb{S}/I\mathbb{S}$
, we get
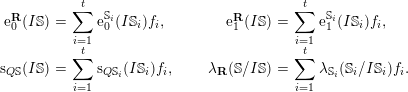 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\text{e}_{0}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i},\quad \quad & \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\text{e}_{1}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i},\\ \text{s}_{Q\mathbb{S}}(I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\text{s}_{Q\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i}, & \unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\unicode[STIX]{x1D706}_{\mathbb{S}_{i}}(\mathbb{S}_{i}/I\mathbb{S}_{i})f_{i}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\text{e}_{0}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i},\quad \quad & \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\text{e}_{1}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i},\\ \text{s}_{Q\mathbb{S}}(I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\text{s}_{Q\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i}, & \unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/I\mathbb{S})\ & =\ & \displaystyle \mathop{\sum }_{i=1}^{t}\unicode[STIX]{x1D706}_{\mathbb{S}_{i}}(\mathbb{S}_{i}/I\mathbb{S}_{i})f_{i}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Note that
Without loss of generality, we may assume that
![]() $\text{r}_{Q\mathbb{S}}(I\mathbb{S})=\text{r}_{Q\mathbb{S}_{1}}(I\mathbb{S}_{1})$
.
$\text{r}_{Q\mathbb{S}}(I\mathbb{S})=\text{r}_{Q\mathbb{S}_{1}}(I\mathbb{S}_{1})$
.
Applying Rossi’s formula [Reference Rossi22, Corollary 1.5] to
![]() $I\mathbb{S}_{1}$
, we get
$I\mathbb{S}_{1}$
, we get
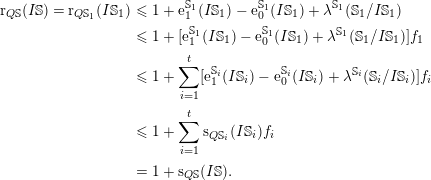 $$\begin{eqnarray}\displaystyle \text{r}_{Q\mathbb{S}}(I\mathbb{S})=\text{r}_{Q\mathbb{S}_{1}}(I\mathbb{S}_{1}) & {\leqslant} & \displaystyle 1+\text{e}_{1}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})-\text{e}_{0}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})+\unicode[STIX]{x1D706}^{\mathbb{S}_{1}}(\mathbb{S}_{1}/I\mathbb{S}_{1})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1+[\text{e}_{1}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})-\text{e}_{0}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})+\unicode[STIX]{x1D706}^{\mathbb{S}_{1}}(\mathbb{S}_{1}/I\mathbb{S}_{1})]f_{1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \displaystyle 1+\mathop{\sum }_{i=1}^{t}[\text{e}_{1}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})-\text{e}_{0}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})+\unicode[STIX]{x1D706}^{\mathbb{S}_{i}}(\mathbb{S}_{i}/I\mathbb{S}_{i})]f_{i}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \displaystyle 1+\mathop{\sum }_{i=1}^{t}\text{s}_{Q\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 1+\text{s}_{Q\mathbb{S}}(I\mathbb{S}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{r}_{Q\mathbb{S}}(I\mathbb{S})=\text{r}_{Q\mathbb{S}_{1}}(I\mathbb{S}_{1}) & {\leqslant} & \displaystyle 1+\text{e}_{1}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})-\text{e}_{0}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})+\unicode[STIX]{x1D706}^{\mathbb{S}_{1}}(\mathbb{S}_{1}/I\mathbb{S}_{1})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1+[\text{e}_{1}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})-\text{e}_{0}^{\mathbb{S}_{1}}(I\mathbb{S}_{1})+\unicode[STIX]{x1D706}^{\mathbb{S}_{1}}(\mathbb{S}_{1}/I\mathbb{S}_{1})]f_{1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \displaystyle 1+\mathop{\sum }_{i=1}^{t}[\text{e}_{1}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})-\text{e}_{0}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})+\unicode[STIX]{x1D706}^{\mathbb{S}_{i}}(\mathbb{S}_{i}/I\mathbb{S}_{i})]f_{i}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \displaystyle 1+\mathop{\sum }_{i=1}^{t}\text{s}_{Q\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 1+\text{s}_{Q\mathbb{S}}(I\mathbb{S}).\nonumber\end{eqnarray}$$
Suppose that
![]() $I=I\mathbb{S}$
. Then,
$I=I\mathbb{S}$
. Then,
![]() $S_{Q}(I)=S_{Q\mathbb{S}}(I\mathbb{S})$
. Recall that by the exact sequence (2), we have that
$S_{Q}(I)=S_{Q\mathbb{S}}(I\mathbb{S})$
. Recall that by the exact sequence (2), we have that
![]() $\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/\mathbf{R})=\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
. Furthermore,
$\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/\mathbf{R})=\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
. Furthermore,
![]() $\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))=-\text{e}_{1}(Q)$
because
$\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))=-\text{e}_{1}(Q)$
because
![]() $\mathbf{R}$
is Buchsbaum (see [Reference Stückrad and Vogel25, Chapter 1, Propositions 2.6, 2.7]). Therefore,
$\mathbf{R}$
is Buchsbaum (see [Reference Stückrad and Vogel25, Chapter 1, Propositions 2.6, 2.7]). Therefore,
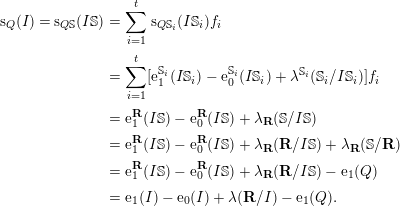 $$\begin{eqnarray}\displaystyle \text{s}_{Q}(I)=\text{s}_{Q\mathbb{S}}(I\mathbb{S}) & = & \displaystyle \displaystyle \mathop{\sum }_{i=1}^{t}\text{s}_{Q\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{i=1}^{t}[\text{e}_{1}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})-\text{e}_{0}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})+\unicode[STIX]{x1D706}^{\mathbb{S}_{i}}(\mathbb{S}_{i}/I\mathbb{S}_{i})]f_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})-\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/I\mathbb{S})\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})-\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbf{R}/I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/\mathbf{R})\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})-\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbf{R}/I\mathbb{S})-\text{e}_{1}(Q)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)-\text{e}_{1}(Q).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{s}_{Q}(I)=\text{s}_{Q\mathbb{S}}(I\mathbb{S}) & = & \displaystyle \displaystyle \mathop{\sum }_{i=1}^{t}\text{s}_{Q\mathbb{S}_{i}}(I\mathbb{S}_{i})f_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{i=1}^{t}[\text{e}_{1}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})-\text{e}_{0}^{\mathbb{S}_{i}}(I\mathbb{S}_{i})+\unicode[STIX]{x1D706}^{\mathbb{S}_{i}}(\mathbb{S}_{i}/I\mathbb{S}_{i})]f_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})-\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/I\mathbb{S})\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})-\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbf{R}/I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/\mathbf{R})\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}^{\mathbf{R}}(I\mathbb{S})-\text{e}_{0}^{\mathbf{R}}(I\mathbb{S})+\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbf{R}/I\mathbb{S})-\text{e}_{1}(Q)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)-\text{e}_{1}(Q).\nonumber\end{eqnarray}$$
Notice that if
![]() $I=Q\mathbb{S}$
, then
$I=Q\mathbb{S}$
, then
![]() $\text{r}_{Q}(I)=1$
, and the conclusion of the theorem holds. Therefore, we may assume that
$\text{r}_{Q}(I)=1$
, and the conclusion of the theorem holds. Therefore, we may assume that
![]() $I\neq Q\mathbb{S}$
. In this case, we have that
$I\neq Q\mathbb{S}$
. In this case, we have that
Now, assume that
![]() $I\subsetneq I\mathbb{S}$
. Note that
$I\subsetneq I\mathbb{S}$
. Note that
![]() $\unicode[STIX]{x1D708}(\mathbb{S})=1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))=1-\text{e}_{1}(Q)$
, by Proposition 4.1(3). Let
$\unicode[STIX]{x1D708}(\mathbb{S})=1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))=1-\text{e}_{1}(Q)$
, by Proposition 4.1(3). Let
![]() $r=\text{r}_{Q\mathbb{S}}(I\mathbb{S})$
. Then,
$r=\text{r}_{Q\mathbb{S}}(I\mathbb{S})$
. Then,
![]() $I^{r+1}\mathbb{S}=QI^{r}\mathbb{S}$
. By [Reference Vasconcelos29, Proposition 1.118], we have
$I^{r+1}\mathbb{S}=QI^{r}\mathbb{S}$
. By [Reference Vasconcelos29, Proposition 1.118], we have
Using Theorem 2.6(3), we obtain
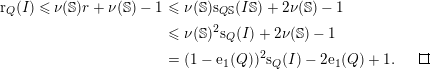 $$\begin{eqnarray}\displaystyle \hspace{35.00005pt}\text{r}_{Q}(I)\leqslant \unicode[STIX]{x1D708}(\mathbb{S})r+\unicode[STIX]{x1D708}(\mathbb{S})-1 & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathbb{S})\text{s}_{Q\mathbb{S}}(I\mathbb{S})+2\unicode[STIX]{x1D708}(\mathbb{S})-1\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathbb{S})^{2}\text{s}_{Q}(I)+2\unicode[STIX]{x1D708}(\mathbb{S})-1\nonumber\\ \displaystyle & = & \displaystyle (1-\text{e}_{1}(Q))^{2}\text{s}_{Q}(I)-2\text{e}_{1}(Q)+1.\hspace{5.0pt}\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hspace{35.00005pt}\text{r}_{Q}(I)\leqslant \unicode[STIX]{x1D708}(\mathbb{S})r+\unicode[STIX]{x1D708}(\mathbb{S})-1 & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathbb{S})\text{s}_{Q\mathbb{S}}(I\mathbb{S})+2\unicode[STIX]{x1D708}(\mathbb{S})-1\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathbb{S})^{2}\text{s}_{Q}(I)+2\unicode[STIX]{x1D708}(\mathbb{S})-1\nonumber\\ \displaystyle & = & \displaystyle (1-\text{e}_{1}(Q))^{2}\text{s}_{Q}(I)-2\text{e}_{1}(Q)+1.\hspace{5.0pt}\square\nonumber\end{eqnarray}$$
Remark 4.4. In the set-up of Theorem 4.3, suppose that
![]() $I\subsetneq I\mathbb{S}$
, and let
$I\subsetneq I\mathbb{S}$
, and let
![]() $r=\text{r}_{Q\mathbb{S}}(I\mathbb{S})$
. Since
$r=\text{r}_{Q\mathbb{S}}(I\mathbb{S})$
. Since
![]() $\mathfrak{m}\mathbb{S}=\mathfrak{m}$
, by Proposition 4.1, we have
$\mathfrak{m}\mathbb{S}=\mathfrak{m}$
, by Proposition 4.1, we have
Thus, we obtain
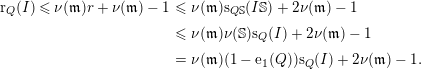 $$\begin{eqnarray}\displaystyle \text{r}_{Q}(I)\leqslant \unicode[STIX]{x1D708}(\mathfrak{m})r+\unicode[STIX]{x1D708}(\mathfrak{m})-1 & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathfrak{m})\text{s}_{Q\mathbb{S}}(I\mathbb{S})+2\unicode[STIX]{x1D708}(\mathfrak{m})-1\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathfrak{m})\unicode[STIX]{x1D708}(\mathbb{S})\text{s}_{Q}(I)+2\unicode[STIX]{x1D708}(\mathfrak{m})-1\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D708}(\mathfrak{m})(1-\text{e}_{1}(Q))\text{s}_{Q}(I)+2\unicode[STIX]{x1D708}(\mathfrak{m})-1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{r}_{Q}(I)\leqslant \unicode[STIX]{x1D708}(\mathfrak{m})r+\unicode[STIX]{x1D708}(\mathfrak{m})-1 & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathfrak{m})\text{s}_{Q\mathbb{S}}(I\mathbb{S})+2\unicode[STIX]{x1D708}(\mathfrak{m})-1\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D708}(\mathfrak{m})\unicode[STIX]{x1D708}(\mathbb{S})\text{s}_{Q}(I)+2\unicode[STIX]{x1D708}(\mathfrak{m})-1\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D708}(\mathfrak{m})(1-\text{e}_{1}(Q))\text{s}_{Q}(I)+2\unicode[STIX]{x1D708}(\mathfrak{m})-1.\nonumber\end{eqnarray}$$
Corollary 4.5. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a two-dimensional Buchsbaum local ring of depth zero. Let
$(\mathbf{R},\mathfrak{m})$
be a two-dimensional Buchsbaum local ring of depth zero. Let
![]() $\mathbb{S}$
be the
$\mathbb{S}$
be the
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
, and let
$\mathbf{R}$
, and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal with a minimal reduction
$\mathfrak{m}$
-primary ideal with a minimal reduction
![]() $Q$
. Set
$Q$
. Set
![]() $\overline{\mathbf{R}}=\mathbf{R}/\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
,
$\overline{\mathbf{R}}=\mathbf{R}/\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
,
![]() $\overline{I}=I\overline{\mathbf{R}}$
and
$\overline{I}=I\overline{\mathbf{R}}$
and
![]() $\overline{Q}=Q\overline{\mathbf{R}}$
.
$\overline{Q}=Q\overline{\mathbf{R}}$
.
-
(1) If
 $\overline{I}=\overline{I}\mathbb{S}$
, then
$\overline{I}=\overline{I}\mathbb{S}$
, then
 $\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+2$
.
$\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+2$
. -
(2) If
 $\overline{I}\subsetneq \overline{I}\mathbb{S}$
, then
$\overline{I}\subsetneq \overline{I}\mathbb{S}$
, then
 $\text{r}_{Q}(I)\leqslant (1-\text{e}_{1}(Q))^{2}\text{s}_{Q}(I)-2\text{e}_{1}(Q)+2$
.
$\text{r}_{Q}(I)\leqslant (1-\text{e}_{1}(Q))^{2}\text{s}_{Q}(I)-2\text{e}_{1}(Q)+2$
.
Proof. Note that
![]() $\overline{\mathbf{R}}$
is a two-dimensional Buchsbaum local ring of positive depth. Let
$\overline{\mathbf{R}}$
is a two-dimensional Buchsbaum local ring of positive depth. Let
![]() $r=\text{r}_{\overline{Q}}(\overline{I})$
. Then,
$r=\text{r}_{\overline{Q}}(\overline{I})$
. Then,
![]() $I^{r+1}-QI^{r}\subset \text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
, which implies that
$I^{r+1}-QI^{r}\subset \text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
, which implies that
![]() $I^{r+2}-QI^{r+1}\subset I\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})=0$
. Thus,
$I^{r+2}-QI^{r+1}\subset I\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})=0$
. Thus,
![]() $\text{r}_{Q}(I)\leqslant \text{r}_{\overline{Q}}(\overline{I})+1$
. Furthermore, the surjective map
$\text{r}_{Q}(I)\leqslant \text{r}_{\overline{Q}}(\overline{I})+1$
. Furthermore, the surjective map
![]() $S_{Q}(I)\rightarrow S_{\overline{Q}}(\overline{I})$
gives
$S_{Q}(I)\rightarrow S_{\overline{Q}}(\overline{I})$
gives
![]() $\text{s}_{Q}(I)\geqslant \text{s}_{\overline{Q}}(\overline{I})$
. Now, the conclusion follows from Theorem 4.3 applied to
$\text{s}_{Q}(I)\geqslant \text{s}_{\overline{Q}}(\overline{I})$
. Now, the conclusion follows from Theorem 4.3 applied to
![]() $\overline{\mathbf{R}}$
.◻
$\overline{\mathbf{R}}$
.◻
Corollary 4.6. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a two-dimensional generalized Cohen–Macaulay local ring. Let
$(\mathbf{R},\mathfrak{m})$
be a two-dimensional generalized Cohen–Macaulay local ring. Let
![]() $\mathbb{S}$
be the
$\mathbb{S}$
be the
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
. Let
$\mathbf{R}$
. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal with a minimal reduction
$\mathfrak{m}$
-primary ideal with a minimal reduction
![]() $Q$
. Suppose that
$Q$
. Suppose that
![]() $\mathbf{R}$
has positive depth.
$\mathbf{R}$
has positive depth.
-
(1) If
 $I=I\mathbb{S}$
, then
$I=I\mathbb{S}$
, then
 $\text{s}_{Q}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
and
$\text{s}_{Q}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\unicode[STIX]{x1D706}(\mathbf{R}/I)+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
and
 $\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1$
.
$\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1$
. -
(2) If
 $I\subsetneq I\mathbb{S}$
, then
$I\subsetneq I\mathbb{S}$
, then
 $\text{r}_{Q}(I)\leqslant (1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R})))^{2}\text{s}_{Q}(I)+2\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))+1$
.
$\text{r}_{Q}(I)\leqslant (1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R})))^{2}\text{s}_{Q}(I)+2\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))+1$
.
Suppose that
![]() $\mathbf{R}$
has depth zero. Set
$\mathbf{R}$
has depth zero. Set
![]() $\overline{\mathbf{R}}=\mathbf{R}/\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
,
$\overline{\mathbf{R}}=\mathbf{R}/\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})$
,
![]() $\overline{I}=I\overline{\mathbf{R}}$
and
$\overline{I}=I\overline{\mathbf{R}}$
and
![]() $\overline{Q}=Q\overline{\mathbf{R}}$
.
$\overline{Q}=Q\overline{\mathbf{R}}$
.
-
(3) If
 $\overline{I}=\overline{I}\mathbb{S}$
, then
$\overline{I}=\overline{I}\mathbb{S}$
, then
 $\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{0}(\mathbf{R}))$
.
$\text{r}_{Q}(I)\leqslant \text{s}_{Q}(I)+1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{0}(\mathbf{R}))$
.
-
(4) If
 $\overline{I}\subsetneq \overline{I}\mathbb{S}$
, then
$\overline{I}\subsetneq \overline{I}\mathbb{S}$
, then
 $\text{r}_{Q}(I)\leqslant (1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R})))^{2}\text{s}_{Q}(I)+2\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))+1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{0}(\mathbf{R}))$
.
$\text{r}_{Q}(I)\leqslant (1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R})))^{2}\text{s}_{Q}(I)+2\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))+1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{0}(\mathbf{R}))$
.
Proof. The proof is almost identical to those of Theorem 4.3 and Corollary 4.5, except that
![]() $\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/\mathbf{R})=\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
,
$\unicode[STIX]{x1D706}_{\mathbf{R}}(\mathbb{S}/\mathbf{R})=\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
,
![]() $\unicode[STIX]{x1D708}(\mathbb{S})\leqslant 1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
and
$\unicode[STIX]{x1D708}(\mathbb{S})\leqslant 1+\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(\mathbf{R}))$
and
![]() $I^{g}\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})=0$
, where
$I^{g}\text{H}_{\mathfrak{m}}^{0}(\mathbf{R})=0$
, where
![]() $g=\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{0}(\mathbf{R}))$
.◻
$g=\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{0}(\mathbf{R}))$
.◻
Example 4.7. [Reference Goto and Ozeki13, Example 2.8]
Let
![]() $k$
be a field, and let
$k$
be a field, and let
![]() $\mathbf{R}=k[[X,Y,Z,W]]/(X,Y)\cap (Z,W)$
, where
$\mathbf{R}=k[[X,Y,Z,W]]/(X,Y)\cap (Z,W)$
, where
![]() $X,Y,Z,W$
are variables. Then,
$X,Y,Z,W$
are variables. Then,
![]() $\mathbf{R}$
is a Buchsbaum ring of dimension 2, depth 1, and
$\mathbf{R}$
is a Buchsbaum ring of dimension 2, depth 1, and
![]() $\text{e}_{1}(Q)=-1$
for all parameter ideals
$\text{e}_{1}(Q)=-1$
for all parameter ideals
![]() $Q$
. Let
$Q$
. Let
![]() $x,y,z,w$
denote the images of
$x,y,z,w$
denote the images of
![]() $X,Y,Z,W$
in
$X,Y,Z,W$
in
![]() $\mathbf{R}$
. Choose an integer
$\mathbf{R}$
. Choose an integer
![]() $q>0$
, and set
$q>0$
, and set
![]() $I=(x^{4},x^{3}y,xy^{3},y^{4})+(z,w)^{q}$
. Notice that the
$I=(x^{4},x^{3}y,xy^{3},y^{4})+(z,w)^{q}$
. Notice that the
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\mathbf{R}$
is
$\mathbf{R}$
is
![]() $\mathbb{S}=k[[z,w]]\oplus k[[x,y]]$
, so that
$\mathbb{S}=k[[z,w]]\oplus k[[x,y]]$
, so that
![]() $I=I\mathbb{S}$
. For every
$I=I\mathbb{S}$
. For every
![]() $n\geqslant 0$
, we have an exact sequence
$n\geqslant 0$
, we have an exact sequence
which gives that
![]() $\unicode[STIX]{x1D706}(\mathbf{R}/I^{n+1})=(q^{2}+16)\binom{n+2}{2}-\frac{q^{2}-q+12}{2}\binom{n+1}{1}-1$
for all
$\unicode[STIX]{x1D706}(\mathbf{R}/I^{n+1})=(q^{2}+16)\binom{n+2}{2}-\frac{q^{2}-q+12}{2}\binom{n+1}{1}-1$
for all
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $\unicode[STIX]{x1D706}(\mathbf{R}/I)=\frac{q^{2}+q+20}{2}$
. Hence,
$\unicode[STIX]{x1D706}(\mathbf{R}/I)=\frac{q^{2}+q+20}{2}$
. Hence,
![]() $\text{e}_{0}(I)=q^{2}+16,\text{e}_{1}(I)=\frac{q^{2}-q+12}{2}$
, so that
$\text{e}_{0}(I)=q^{2}+16,\text{e}_{1}(I)=\frac{q^{2}-q+12}{2}$
, so that
![]() $\text{e}_{0}(I)-\unicode[STIX]{x1D706}(\mathbf{R}/I)=\text{e}_{1}(I).$
$\text{e}_{0}(I)-\unicode[STIX]{x1D706}(\mathbf{R}/I)=\text{e}_{1}(I).$
Let
![]() $Q=(x^{4}-z^{q},y^{4}-w^{q})$
. It is easy to see that
$Q=(x^{4}-z^{q},y^{4}-w^{q})$
. It is easy to see that
![]() $Q$
is a minimal reduction of
$Q$
is a minimal reduction of
![]() $I$
with
$I$
with
![]() $\text{r}_{Q}(I)=2$
. By Theorem 4.3(1), we have that
$\text{r}_{Q}(I)=2$
. By Theorem 4.3(1), we have that
![]() $\text{s}_{Q}(I)=1$
. Hence, the bound of Theorem 4.3(1) is sharp:
$\text{s}_{Q}(I)=1$
. Hence, the bound of Theorem 4.3(1) is sharp:
![]() $\text{r}_{Q}(I)=\text{s}_{Q}(I)+1$
.
$\text{r}_{Q}(I)=\text{s}_{Q}(I)+1$
.
Sally modules for Buchsbaum rings
The preceding section requires formulas for the multiplicity
![]() $\text{s}_{Q}(I)$
of the Sally module of
$\text{s}_{Q}(I)$
of the Sally module of
![]() $I$
relative to
$I$
relative to
![]() $Q$
, at least in the case that
$Q$
, at least in the case that
![]() $\mathbf{R}$
is Buchsbaum. We recall a result of Corso [Reference Corso3, Proposition 2.8].
$\mathbf{R}$
is Buchsbaum. We recall a result of Corso [Reference Corso3, Proposition 2.8].
Proposition 4.8. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d$
, let
$d$
, let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal, and let
$\mathfrak{m}$
-primary ideal, and let
![]() $Q$
be one of its minimal reductions. Suppose that
$Q$
be one of its minimal reductions. Suppose that
![]() $\dim S_{Q}(I)=d$
. Then,
$\dim S_{Q}(I)=d$
. Then,
The following was proved in [Reference Ozeki20, Proposition 2.5(1)(i)], but we give a slightly different proof for the result, which uses the approximation complex.
Corollary 4.9. Let
![]() $(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
$(\mathbf{R},\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d$
, let
$d$
, let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal, and let
$\mathfrak{m}$
-primary ideal, and let
![]() $Q$
be one of its minimal reductions. Suppose that
$Q$
be one of its minimal reductions. Suppose that
![]() $\dim S_{Q}(I)=d$
. Let
$\dim S_{Q}(I)=d$
. Let
![]() $\unicode[STIX]{x1D711}$
be the matrix of syzygies of
$\unicode[STIX]{x1D711}$
be the matrix of syzygies of
![]() $Q$
. If
$Q$
. If
![]() $Q$
is generated by a d-sequence and
$Q$
is generated by a d-sequence and
![]() $I_{1}(\unicode[STIX]{x1D711})\subset I$
, then
$I_{1}(\unicode[STIX]{x1D711})\subset I$
, then
Proof. Let
![]() $\overline{G}=\text{gr}_{Q}(\mathbf{R})\otimes \mathbf{R}/I$
. By the proof of [Reference Corso3, Proposition 2.8], we have
$\overline{G}=\text{gr}_{Q}(\mathbf{R})\otimes \mathbf{R}/I$
. By the proof of [Reference Corso3, Proposition 2.8], we have
Set
![]() $\mathbf{B}=\mathbf{R}[T_{1},\ldots ,T_{d}]$
. Since
$\mathbf{B}=\mathbf{R}[T_{1},\ldots ,T_{d}]$
. Since
![]() $Q$
is generated by a
$Q$
is generated by a
![]() $d$
-sequence, the approximation complex
$d$
-sequence, the approximation complex
is acyclic (see [Reference Herzog, Simis and Vasconcelos14, Theorem 5.6]). By tensoring this complex by
![]() $\mathbf{R}/I$
, we get the exact sequence
$\mathbf{R}/I$
, we get the exact sequence
Since
![]() $I_{1}(\unicode[STIX]{x1D711})\subset I$
, the mapping
$I_{1}(\unicode[STIX]{x1D711})\subset I$
, the mapping
![]() $\unicode[STIX]{x1D719}$
is trivial, so that
$\unicode[STIX]{x1D719}$
is trivial, so that
![]() $\text{e}_{0}(\overline{G})=\unicode[STIX]{x1D706}(\mathbf{R}/I)$
.◻
$\text{e}_{0}(\overline{G})=\unicode[STIX]{x1D706}(\mathbf{R}/I)$
.◻
Remark 4.10. One instance when
![]() $I_{1}(\unicode[STIX]{x1D711})\subset I$
occurs if
$I_{1}(\unicode[STIX]{x1D711})\subset I$
occurs if
![]() $\mathbf{R}$
is unmixed and
$\mathbf{R}$
is unmixed and
![]() $I$
is integrally closed, according to [Reference Ratliff21, Proposition 3.1].
$I$
is integrally closed, according to [Reference Ratliff21, Proposition 3.1].