Hostname: page-component-5c6d5d7d68-7tdvq Total loading time: 0 Render date: 2024-08-16T22:43:15.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Scalar curvatures of conformal metrics on Sn

Published online by Cambridge University Press:  22 January 2016

Shigeo Kawai
Shigeo Kawai*
Affiliation:
Department of Mathematics, Faculty of Education Saga University, Saga 840, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the following problem: Given a smooth function K on the n-dimensional unit sphere Sn(n ≥ 3) with its canonical metric g0, is it possible to find a pointwise conformal metric 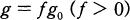which has K as its scalar curvature? This problem was presented by J. L. Kazdan and F. W. Warner. The associated problem for Gaussian curvature in dimension 2 had been presented by L. Nirenberg several years before.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 140 , December 1995 , pp. 151 - 166
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[ 1 ] Aubin, J. P. and Ekeland, I., Applied Nonlinear Analysis, Wiley-Interscience, New York, 1984.Google Scholar
[ 2 ] Bahri, A. and Coron, C., The scalar curvature problem on the three-dimensionalsphere, J. Funct. Anal., 95 (1991), 106–172.Google Scholar
[ 3 ] Bourguignon, J. P. and Ezin, J. P., Scalar curvature functions in a conformal class of metrics and conformal transformations, Trans. Amer. Math. Soc, 301 (1987), 723–736.CrossRefGoogle Scholar
[ 4 ] Brezis, H. and Lieb, E., A relation between pointwise convergence of functions and convergence of functionals, Proc. Amer. Math., Soc, (1983), 486–490.Google Scholar
[ 5 ] Chang, S.-Y. and Yang, P. C., Prescribing Gaussian curvature on S2 , Acta Math., 159 (1987), 215–259.CrossRefGoogle Scholar
[ 6 ] Chang, S.-Y. and Yang, P. C., Conformal deformation of metrics on S2 , J. Diff. Geom., 27 (1988), 259–296.Google Scholar
[ 7 ] Chang, S.-Y. and Yang, P. C., A perturbation result in prescribing scalar curvature on Sn , Duke Math. J., 64 (1991), 27–69.Google Scholar
[ 8 ] Chen, W. and Ding, W., Scalar curvatures on S2 , Trans. Amer. Math. Soc, 303 (1987), 365–382.Google Scholar
[ 9 ] Ekeland, I., On the variational principle, J. Math. Anal. Appl., 47, 324–353.CrossRefGoogle Scholar
[10] Escobar, J. F. and Schoen, R., Conformal metrics with prescribed scalar curvature, Invent. Math., 86 (1986), 243–254.Google Scholar
[11] Han, Z.-C., Prescribing Gaussian curvature on 5, Duke Math. J., 61 (1990). 679–703.Google Scholar
[12] Hong, C., A best constant and the Gaussian curvature, Proc. Amer. Math. Soc, 97 (1986), 737–747.Google Scholar
[13] Kazdan, J. L. and Warner, F. W., Curvature functions for compact 2-manifolds, Ann. of Math., 99 (1974), 14–74.Google Scholar
[14] Kazdan, J. L. and Warner, F. W., Scalar curvature and conformal deformation of Riemannian structure, J. Diff. Geom., 10 (1975), 113–134.Google Scholar
[15] Moser, J., On a nonlinear problem in differential geometry, Dynamical System, Academic Press, New York, 1973.Google Scholar
[16] Shuzhong, S., Ekeland’s variational principle and the mountain pass lemma, Acta Mathematica Sinica, 1 (1985), 348–355.CrossRefGoogle Scholar
[17] Stampacchia, G., On some regular multiple integral problems in the calculus of variations, Comm. Pure Appl. Math., 16 (1963), 383–421.CrossRefGoogle Scholar
[18] Struwe, M., Variational Methods, Springer, Berlin Heidelberg, 1990.Google Scholar
[19] Trudinger, N. S., Remarks concerning the conformal deformation of Riemannian structures on compact manifolds, Ann. Scuola Norm. Sup. Pisa, 22 (1968), 265–274.Google Scholar