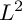1 Introduction
Multiplier ideal sheaves for singular Hermitian metrics on line bundles are very important and have many applications in many fields. Indeed, Nadel introduced a notion of multiplier ideal sheaves and applied it to show the existence of Kähler–Einstein metrics of positive scalar curvature on certain compact complex manifolds in [Reference Nadel19]. As another example, Siu established the invariance of plurigenera by using this notion [Reference Siu23]. Nadel also proved a cohomology vanishing theorem with coefficients in multiplier ideal sheaves, which is one generalization of the Kawamata–Viehweg vanishing theorem. This vanishing theorem has been applied in algebraic and complex geometry.
In his paper, Nadel showed the following celebrated result: a multiplier ideal sheaf associated with a plurisubharmonic function is coherent. An important technique of the proof is an
![]() $L^2$
-estimate of the
$L^2$
-estimate of the
![]() $\overline {\partial }$
-equation of Hörmander type [Reference Hörmander9].
$\overline {\partial }$
-equation of Hörmander type [Reference Hörmander9].
A higher rank analogue of a multiplier ideal sheaf associated with a singular Hermitian metric on a vector bundle has been also studied. This notion has been recognized as important. However, the coherence of it is only known in few cases (cf. [Reference de Cataldo4, Prop. 4.1.3], [Reference Hosono10, Th. 1.1]). If a metric has some strong positivity like Nakano positivity, it is known that the higher rank analogue of the multiplier ideal sheaf is coherent ([Reference Hosono and Inayama11, Th. 1.4], [Reference Inayama14, Prop. 4.4], [Reference Iwai15, Th. 1.2]). Hence, it is natural to ask whether the higher rank analogue of the multiplier ideal sheaf is coherent if the associated metric has only Griffiths positivity, which is a strictly weaker notion than Nakano positivity.
Conjecture 1.1. Let
![]() $(E, h)$
be a holomorphic vector bundle over an n-dimensional complex manifold X with a singular Hermitian metric h. If h is Griffiths semipositive, the higher rank analogue of the multiplier ideal sheaf
$(E, h)$
be a holomorphic vector bundle over an n-dimensional complex manifold X with a singular Hermitian metric h. If h is Griffiths semipositive, the higher rank analogue of the multiplier ideal sheaf
![]() $\mathcal {E}(h)$
is coherent.
$\mathcal {E}(h)$
is coherent.
This conjecture seems a tough problem due to the following reasons. First, we cannot apply an
![]() $L^2$
-estimate of the
$L^2$
-estimate of the
![]() $\overline {\partial }$
-equation directly even if h is smooth. That is because a kind of the solvability of the
$\overline {\partial }$
-equation directly even if h is smooth. That is because a kind of the solvability of the
![]() $\overline {\partial }$
-equation with
$\overline {\partial }$
-equation with
![]() $L^2$
-estimates in the optimal setting is equivalent to the Nakano positivity of the metric [Reference Deng, Ning, Wang and Zhou8, Th. 1.1]. Second, it might be useful to get an approximating sequence
$L^2$
-estimates in the optimal setting is equivalent to the Nakano positivity of the metric [Reference Deng, Ning, Wang and Zhou8, Th. 1.1]. Second, it might be useful to get an approximating sequence
![]() $\{ h_\nu \}$
of h such that the Chern curvature of
$\{ h_\nu \}$
of h such that the Chern curvature of
![]() $h_\nu $
is uniformly bounded below in the sense of Nakano. However, it is known that this procedure cannot be done simply by using the standard approximation defined by convolution [Reference Hosono10, Th. 1.2].
$h_\nu $
is uniformly bounded below in the sense of Nakano. However, it is known that this procedure cannot be done simply by using the standard approximation defined by convolution [Reference Hosono10, Th. 1.2].
In order to use the technique of Hörmander’s
![]() $L^2$
-estimate, we need to devise some settings. By imposing conditions on the singularity of h, we can give a partial answer to the conjecture.
$L^2$
-estimate, we need to devise some settings. By imposing conditions on the singularity of h, we can give a partial answer to the conjecture.
Theorem 1.2. Let
![]() $(E, h)$
be a holomorphic vector bundle over an n-dimensional complex manifold X with a Griffiths semipositive singular Hermitian metric h. If the unbounded locus
$(E, h)$
be a holomorphic vector bundle over an n-dimensional complex manifold X with a Griffiths semipositive singular Hermitian metric h. If the unbounded locus
![]() $L(\det h)$
of
$L(\det h)$
of
![]() $\det h$
is discrete, the higher rank analogue of the multiplier ideal sheaf
$\det h$
is discrete, the higher rank analogue of the multiplier ideal sheaf
![]() $\mathcal {S}^m\mathcal {E}(S^mh)$
is coherent for every
$\mathcal {S}^m\mathcal {E}(S^mh)$
is coherent for every
![]() $m\in \mathbb {N}$
. Here,
$m\in \mathbb {N}$
. Here,
![]() $\mathcal {S}^m\mathcal {E}(S^mh)$
is the sheaf of germs of local holomorphic sections of the mth symmetric power
$\mathcal {S}^m\mathcal {E}(S^mh)$
is the sheaf of germs of local holomorphic sections of the mth symmetric power
![]() $S^mE$
of E, which is square integrable with respect to
$S^mE$
of E, which is square integrable with respect to
![]() $S^mh$
(see Definition 2.5 for the precise definition).
$S^mh$
(see Definition 2.5 for the precise definition).
The condition on h in the main theorem appears naturally when h has some kind of symmetry. Indeed, as an application of the main theorem, we get the following result.
Corollary 1.3. Let E be the trivial vector bundle
![]() $E=\mathbb {B}^n\times \mathbb {C}^r$
over the unit ball
$E=\mathbb {B}^n\times \mathbb {C}^r$
over the unit ball
![]() $\mathbb {B}^n:=\{ (z_1, \dots , z_n)\in \mathbb {C}^n\mid |z|^2<1\}$
, and let h be a Griffiths seminegative singular Hermitian metric on E. If
$\mathbb {B}^n:=\{ (z_1, \dots , z_n)\in \mathbb {C}^n\mid |z|^2<1\}$
, and let h be a Griffiths seminegative singular Hermitian metric on E. If
![]() $\det h$
is a radial function, that is, depending only on the radius
$\det h$
is a radial function, that is, depending only on the radius
![]() $|z|$
,
$|z|$
,
![]() $\mathcal {S}^m\mathcal {E}^\star (S^mh^\star )$
is coherent for every
$\mathcal {S}^m\mathcal {E}^\star (S^mh^\star )$
is coherent for every
![]() $m\in \mathbb {N}$
. Especially, if h is spherically symmetric (see Definition 2.6),
$m\in \mathbb {N}$
. Especially, if h is spherically symmetric (see Definition 2.6),
![]() $\mathcal {S}^m\mathcal {E}^\star (S^mh^\star )$
is coherent for every
$\mathcal {S}^m\mathcal {E}^\star (S^mh^\star )$
is coherent for every
![]() $m\in \mathbb {N}$
.
$m\in \mathbb {N}$
.
2 Preliminaries
In this section, we give properties of singular Hermitian metrics on holomorphic vector bundles. First, let us recall positivity notions for smooth Hermitian vector bundles. Let
![]() $(E,h)$
be a smooth Hermitian vector bundle over a complex manifold X. We denote by
$(E,h)$
be a smooth Hermitian vector bundle over a complex manifold X. We denote by
![]() $\Theta _{E,h}$
the Chern curvature of
$\Theta _{E,h}$
the Chern curvature of
![]() $(E, h)$
and by
$(E, h)$
and by
![]() $\widetilde {\Theta }_{E,h}$
the associated Hermitian form on
$\widetilde {\Theta }_{E,h}$
the associated Hermitian form on
![]() $T_X\otimes E$
. Then
$T_X\otimes E$
. Then
![]() $(E,h)$
is said to be Nakano positive if
$(E,h)$
is said to be Nakano positive if
![]() $\widetilde {\Theta }_{E,h}(\tau , \tau )>0$
for all nonzero elements
$\widetilde {\Theta }_{E,h}(\tau , \tau )>0$
for all nonzero elements
![]() $\tau \in T_X\otimes E$
. If
$\tau \in T_X\otimes E$
. If
![]() $\widetilde {\Theta }_{E,h}(v\otimes s, v\otimes s)>0$
for all nonzero elements
$\widetilde {\Theta }_{E,h}(v\otimes s, v\otimes s)>0$
for all nonzero elements
![]() $v\in T_X$
and
$v\in T_X$
and
![]() $s\in E$
,
$s\in E$
,
![]() $(E,h)$
is said to be Griffiths positive. Corresponding negativity is defined similarly. It is clear that Nakano positivity is a stronger positivity notion than Griffiths positivity. It is also known that these notions do not coincide [Reference Demailly6, Chap. VII, Exam. 8.4]. For Hermitian forms A and B on
$(E,h)$
is said to be Griffiths positive. Corresponding negativity is defined similarly. It is clear that Nakano positivity is a stronger positivity notion than Griffiths positivity. It is also known that these notions do not coincide [Reference Demailly6, Chap. VII, Exam. 8.4]. For Hermitian forms A and B on
![]() $T_X\otimes E$
, we write
$T_X\otimes E$
, we write
![]() $A\geq _{\mathrm {Nak}.}B$
(resp.,
$A\geq _{\mathrm {Nak}.}B$
(resp.,
![]() $A\geq _{\mathrm {Grif}.}B$
) if
$A\geq _{\mathrm {Grif}.}B$
) if
![]() $A(\tau ,\tau )\geq B(\tau ,\tau )$
(resp.,
$A(\tau ,\tau )\geq B(\tau ,\tau )$
(resp.,
![]() $A(v\otimes s, v\otimes s)\geq B(v\otimes s, v\otimes s)$
) for any
$A(v\otimes s, v\otimes s)\geq B(v\otimes s, v\otimes s)$
) for any
![]() $\tau \in T_X\otimes E$
( resp.,
$\tau \in T_X\otimes E$
( resp.,
![]() $v\in T_X$
and
$v\in T_X$
and
![]() $s\in E$
).
$s\in E$
).
Next, we show positivity notions for singular Hermitian metrics. For the definition of singular Hermitian metrics, see [Reference Berndtsson and Păun3, §3] or [Reference Raufi21, Def. 1.1].
Definition 2.1 ([Reference Berndtsson and Păun3, Defs. 3.1 and 3.2], [Reference Raufi21, §2]).
Let
![]() $(E,h)$
be a singular Hermitian bundle over a complex manifold X. Then
$(E,h)$
be a singular Hermitian bundle over a complex manifold X. Then
![]() $(E,h)$
is said to be:
$(E,h)$
is said to be:
-
1. Griffiths seminegative if
 $\log |s|^2_h$
(or
$\log |s|^2_h$
(or
 $|s|^2_h$
) is plurisubharmonic for any local holomorphic section s of E.
$|s|^2_h$
) is plurisubharmonic for any local holomorphic section s of E. -
2. Griffiths semipositive if the dual metric
 $h^\star $
on
$h^\star $
on
 $E^\star $
is Griffiths seminegative.
$E^\star $
is Griffiths seminegative.
Then we introduce the definition of unbounded loci. Let
![]() $\varphi $
be a plurisubharmonic function on a complex manifold X. It is known that the unbounded locus of
$\varphi $
be a plurisubharmonic function on a complex manifold X. It is known that the unbounded locus of
![]() $\varphi $
is defined to be the set of points
$\varphi $
is defined to be the set of points
![]() $x\in X$
such that
$x\in X$
such that
![]() $\varphi $
is unbounded on every neighborhood of x. We denote it by
$\varphi $
is unbounded on every neighborhood of x. We denote it by
![]() $L(\varphi )$
. For a general singular Hermitian metric on a line bundle, the unbounded locus is defined similarly.
$L(\varphi )$
. For a general singular Hermitian metric on a line bundle, the unbounded locus is defined similarly.
Definition 2.2 (cf. [Reference Lärkäng, Raufi, Ruppenthal and Sera17, Def. 3.3]).
Let
![]() $(L,g)$
be a singular Hermitian line bundle over a complex manifold X. Suppose that g is seminegative. The unbounded locus
$(L,g)$
be a singular Hermitian line bundle over a complex manifold X. Suppose that g is seminegative. The unbounded locus
![]() $L(g)$
of g is defined as follows:
$L(g)$
of g is defined as follows:
![]() $x\in X$
is in
$x\in X$
is in
![]() $L(g)$
if and only if for an open coordinate
$L(g)$
if and only if for an open coordinate
![]() $U_\alpha $
of x which trivializes
$U_\alpha $
of x which trivializes
![]() $(L|_{U_\alpha }\cong \mathbb {C}, g|_{U_\alpha }=e^{\varphi _\alpha })$
,
$(L|_{U_\alpha }\cong \mathbb {C}, g|_{U_\alpha }=e^{\varphi _\alpha })$
,
![]() $x \in L(\varphi _\alpha )$
.
$x \in L(\varphi _\alpha )$
.
Similarly, if g is semipositive, the unbounded locus
![]() $L(g)$
of g is defined by
$L(g)$
of g is defined by
![]() $L(g):=L(g^\star )$
.
$L(g):=L(g^\star )$
.
Note that if
![]() $(L, g)$
has seminegative curvature, the above
$(L, g)$
has seminegative curvature, the above
![]() $\varphi _\alpha $
is a plurisubharmonic function. Thus,
$\varphi _\alpha $
is a plurisubharmonic function. Thus,
![]() $L(\varphi _\alpha )$
is well defined. For another trivialization
$L(\varphi _\alpha )$
is well defined. For another trivialization
![]() $U_\beta $
, we have that
$U_\beta $
, we have that
![]() $\varphi _\alpha =\log |g_{\alpha \beta }|^2+\varphi _\beta $
, where
$\varphi _\alpha =\log |g_{\alpha \beta }|^2+\varphi _\beta $
, where
![]() $g_{\alpha \beta }$
is a transition function of L on
$g_{\alpha \beta }$
is a transition function of L on
![]() $U_\alpha \cap U_\beta $
. Since
$U_\alpha \cap U_\beta $
. Since
![]() $\log |g_{\alpha \beta }|^2$
is locally bounded, for any point
$\log |g_{\alpha \beta }|^2$
is locally bounded, for any point
![]() $x\in U_\alpha \cap U_\beta $
,
$x\in U_\alpha \cap U_\beta $
,
![]() $x\in L(\varphi _\alpha )$
if and only if
$x\in L(\varphi _\alpha )$
if and only if
![]() $x\in L(\varphi _\beta )$
. Hence, the unbounded locus of g can be defined globally.
$x\in L(\varphi _\beta )$
. Hence, the unbounded locus of g can be defined globally.
We have another description of
![]() $L(g)$
. We take an open trivializing covering
$L(g)$
. We take an open trivializing covering
![]() $\{ U_\alpha \}_{\alpha \in \Lambda }$
of X and set
$\{ U_\alpha \}_{\alpha \in \Lambda }$
of X and set
![]() $h|_{U_\alpha }=:e^{\varphi _\alpha }$
. Then
$h|_{U_\alpha }=:e^{\varphi _\alpha }$
. Then
![]() $L(g)=\cup _{\alpha \in \Lambda } L(\varphi _\alpha )$
. This definition is independent of the choice of open coverings for the same reason as above. Set
$L(g)=\cup _{\alpha \in \Lambda } L(\varphi _\alpha )$
. This definition is independent of the choice of open coverings for the same reason as above. Set
![]() $B(\varphi _\alpha ):=U_\alpha \setminus L(\varphi _\alpha )$
, where
$B(\varphi _\alpha ):=U_\alpha \setminus L(\varphi _\alpha )$
, where
![]() $\varphi _\alpha $
is locally bounded, and
$\varphi _\alpha $
is locally bounded, and
![]() $B(g)=\cup _{\alpha \in \Lambda }B(\varphi _\alpha )$
. We clearly see that
$B(g)=\cup _{\alpha \in \Lambda }B(\varphi _\alpha )$
. We clearly see that
![]() $L(g)\cap B(g)=\emptyset $
. Indeed, if there is an element
$L(g)\cap B(g)=\emptyset $
. Indeed, if there is an element
![]() $x\in L(g)\cap B(g)$
, there exist
$x\in L(g)\cap B(g)$
, there exist
![]() $\alpha \in \Lambda $
and
$\alpha \in \Lambda $
and
![]() $\beta \in \Lambda $
such that
$\beta \in \Lambda $
such that
![]() $x\in L(\varphi _\alpha )$
and
$x\in L(\varphi _\alpha )$
and
![]() $x\in B(\varphi _\beta )$
. Note that
$x\in B(\varphi _\beta )$
. Note that
![]() $x\in U_\alpha \cap U_\beta $
. The above argument implies that
$x\in U_\alpha \cap U_\beta $
. The above argument implies that
![]() $x\in L(\varphi _\beta )$
as well, but this contradicts the fact that
$x\in L(\varphi _\beta )$
as well, but this contradicts the fact that
![]() $L(\varphi _\beta )\cap B(\varphi _\beta )=\emptyset $
. Hence,
$L(\varphi _\beta )\cap B(\varphi _\beta )=\emptyset $
. Hence,
![]() $X=L(g)\bigsqcup B(g)$
. It is clear that
$X=L(g)\bigsqcup B(g)$
. It is clear that
![]() $B(g)$
is an open subset. Therefore, we see that
$B(g)$
is an open subset. Therefore, we see that
![]() $L(g)$
is a closed subset. If E is a vector bundle with a Griffiths semipositive singular Hermitian metric h,
$L(g)$
is a closed subset. If E is a vector bundle with a Griffiths semipositive singular Hermitian metric h,
![]() $(\det E, \det h)$
is semipositive as well. Thus, we can define the unbounded locus
$(\det E, \det h)$
is semipositive as well. Thus, we can define the unbounded locus
![]() $L(\det h)$
as in Definition 2.2.
$L(\det h)$
as in Definition 2.2.
Next, we introduce an
![]() $L^2$
-estimate of Hörmander type. In this paper, we use the following form.
$L^2$
-estimate of Hörmander type. In this paper, we use the following form.
Theorem 2.3 ([Reference Demailly5], [Reference Demailly6, Chap. VIII, Th. 6.1]).
Let
![]() $(X, \widehat {\omega })$
be a complete Kähler manifold, let
$(X, \widehat {\omega })$
be a complete Kähler manifold, let
![]() $\omega $
be another Kähler metric which is not necessarily complete, and let
$\omega $
be another Kähler metric which is not necessarily complete, and let
![]() $(E, h)\to X$
be a Nakano semipositive vector bundle. Then, for any
$(E, h)\to X$
be a Nakano semipositive vector bundle. Then, for any
![]() $\overline {\partial }$
-closed E-valued
$\overline {\partial }$
-closed E-valued
![]() $(n,q)$
-form u with
$(n,q)$
-form u with
![]() $q>0$
and
$q>0$
and
![]() $\int _X \langle [\sqrt {-1}\Theta _{E,h}, \Lambda _\omega ]^{-1}u,u\rangle \mathrm {d}V_\omega <+\infty $
, there exists a solution of
$\int _X \langle [\sqrt {-1}\Theta _{E,h}, \Lambda _\omega ]^{-1}u,u\rangle \mathrm {d}V_\omega <+\infty $
, there exists a solution of
![]() $\overline {\partial } \alpha =u$
satisfying
$\overline {\partial } \alpha =u$
satisfying
 $$ \begin{align*} \int_X |\alpha|^2_{\omega,h}\mathrm{d}V_\omega\leq \int_X \langle [\sqrt{-1}\Theta_{E,h}, \Lambda_\omega]^{-1}u,u\rangle_{\omega,h} \mathrm{d}V_\omega, \end{align*} $$
$$ \begin{align*} \int_X |\alpha|^2_{\omega,h}\mathrm{d}V_\omega\leq \int_X \langle [\sqrt{-1}\Theta_{E,h}, \Lambda_\omega]^{-1}u,u\rangle_{\omega,h} \mathrm{d}V_\omega, \end{align*} $$
where
![]() $\langle \cdot , \cdot \rangle _{\omega , h}$
denotes the pointwise metric with respect to
$\langle \cdot , \cdot \rangle _{\omega , h}$
denotes the pointwise metric with respect to
![]() $\omega $
and h,
$\omega $
and h,
![]() $[\cdot , \cdot ]$
denotes the graded Lie bracket, and
$[\cdot , \cdot ]$
denotes the graded Lie bracket, and
![]() $\mathrm {d}V_\omega =\omega ^n/n!$
.
$\mathrm {d}V_\omega =\omega ^n/n!$
.
Then we recall the following result, which clarifies the relationship between Griffiths positivity and Nakano positivity.
Theorem 2.4 ([Reference Demailly and Skoda7], [Reference Berndtsson1], [Reference Liu, Sun and Yang18]).
Let
![]() $(E,h)$
be a smooth Hermitian vector bundle. If
$(E,h)$
be a smooth Hermitian vector bundle. If
![]() $(E,h)$
is Griffiths semipositive,
$(E,h)$
is Griffiths semipositive,
![]() $(S^mE\otimes \det E, S^mh\otimes \det h)$
is Nakano semipositive for every
$(S^mE\otimes \det E, S^mh\otimes \det h)$
is Nakano semipositive for every
![]() $m\in \mathbb {N}$
, where
$m\in \mathbb {N}$
, where
![]() $S^mE$
is the mth symmetric power of E.
$S^mE$
is the mth symmetric power of E.
In this paper, we call this theorem a Demaill–Skoda-type result since this type of theorem was initially found by Demailly and Skoda [Reference Demailly and Skoda7]. This result plays a crucial role in the article. Then we introduce a notion of a higher rank analogue of a multiplier ideal sheaf.
Definition 2.5 ([Reference de Cataldo4, Def. 2.3.1]).
Let
![]() $(E,h)$
be a singular Hermitian vector bundle over a complex manifold X. Then we define the higher rank analogue of the multiplier ideal sheaf
$(E,h)$
be a singular Hermitian vector bundle over a complex manifold X. Then we define the higher rank analogue of the multiplier ideal sheaf
![]() $\mathcal {E}(h)$
by
$\mathcal {E}(h)$
by
where
![]() $\mathcal {O}_X(E)$
is the locally free sheaf associated to E. Similarly, we define
$\mathcal {O}_X(E)$
is the locally free sheaf associated to E. Similarly, we define
![]() $\mathcal {S}^m\mathcal {E}(S^mh)$
by
$\mathcal {S}^m\mathcal {E}(S^mh)$
by
At the last of this section, we introduce a notion of spherically symmetric singular Hermitian metrics on the trivial vector bundle over the unit ball. This is one generalization of
![]() $S^1$
-invariant singular Hermitian metrics over the disk, which was introduced by Berndtsson [Reference Berndtsson2].
$S^1$
-invariant singular Hermitian metrics over the disk, which was introduced by Berndtsson [Reference Berndtsson2].
Definition 2.6. Let E be the trivial vector bundle
![]() $E=\mathbb {B}^n\times \mathbb {C}^r$
over the unit ball
$E=\mathbb {B}^n\times \mathbb {C}^r$
over the unit ball
![]() $\mathbb {B}^n$
, and let h be a Griffiths seminegative singular Hermitian metric. We say that h is spherically symmetric if for any
$\mathbb {B}^n$
, and let h be a Griffiths seminegative singular Hermitian metric. We say that h is spherically symmetric if for any
![]() $u\in \mathbb {C}^r$
,
$u\in \mathbb {C}^r$
,
![]() $|u|_{h(z)}=|u|_{h(|z|)}$
for
$|u|_{h(z)}=|u|_{h(|z|)}$
for
![]() $z\in \Delta ^n$
. In other words,
$z\in \Delta ^n$
. In other words,
![]() $|u|_{h(z)}$
is a radial function for any
$|u|_{h(z)}$
is a radial function for any
![]() $u\in V$
.
$u\in V$
.
Berndtsson studied Lelong numbers and integrability indices for
![]() $S^1$
-invariant singular metrics and obtained many applications in [Reference Berndtsson2]. In this sense, a symmetric singular Hermitian metric is an important notion. We also have another generalization such as
$S^1$
-invariant singular metrics and obtained many applications in [Reference Berndtsson2]. In this sense, a symmetric singular Hermitian metric is an important notion. We also have another generalization such as
![]() $\mathbf {T}^n$
-invariant or
$\mathbf {T}^n$
-invariant or
![]() $S^1$
-invariant singular Hermitian metrics, where
$S^1$
-invariant singular Hermitian metrics, where
![]() $\mathbf {T}^n$
is the unit torus in
$\mathbf {T}^n$
is the unit torus in
![]() $\mathbb {C}^n$
. However, since they do not fit the setting of the main theorem, we do not consider them in this article.
$\mathbb {C}^n$
. However, since they do not fit the setting of the main theorem, we do not consider them in this article.
3
 $L^2$
-estimates for singular Hermitian metrics
$L^2$
-estimates for singular Hermitian metrics
In this section, we show an
![]() $L^2$
-estimate for singular Hermitian metrics on holomorphic vector bundles and give a proof of the main theorem. First, we prove the following result.
$L^2$
-estimate for singular Hermitian metrics on holomorphic vector bundles and give a proof of the main theorem. First, we prove the following result.
Theorem 3.1. Let
![]() $(M, \omega )$
be a Stein manifold with a Kähler metric
$(M, \omega )$
be a Stein manifold with a Kähler metric
![]() $\omega $
. We also let
$\omega $
. We also let
![]() $(E=M\times \mathbb {C}^r, h)$
be the trivial holomorphic vector bundle with a Griffiths semipositive singular Hermitian metric h, and let
$(E=M\times \mathbb {C}^r, h)$
be the trivial holomorphic vector bundle with a Griffiths semipositive singular Hermitian metric h, and let
![]() $\psi $
be a smooth strictly plurisubharmonic function with
$\psi $
be a smooth strictly plurisubharmonic function with
![]() $\sqrt {-1}\partial \overline {\partial } \psi \geq \varepsilon \omega $
for a positive constant
$\sqrt {-1}\partial \overline {\partial } \psi \geq \varepsilon \omega $
for a positive constant
![]() $\varepsilon>0$
. Then, for any
$\varepsilon>0$
. Then, for any
![]() $\overline {\partial } $
-closed
$\overline {\partial } $
-closed
![]() $S^mE\otimes \det E$
-valued
$S^mE\otimes \det E$
-valued
![]() $(n,q)$
-form u with finite
$(n,q)$
-form u with finite
![]() $L^2$
-norm, there exists an
$L^2$
-norm, there exists an
![]() $S^mE\otimes \det E$
-valued
$S^mE\otimes \det E$
-valued
![]() $(n,q-1)$
-form
$(n,q-1)$
-form
![]() $\alpha $
such that
$\alpha $
such that
![]() $\overline {\partial } \alpha =u$
and
$\overline {\partial } \alpha =u$
and
 $$ \begin{align*} \int_M |\alpha|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega \leq \frac{1}{q\varepsilon} \int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega. \end{align*} $$
$$ \begin{align*} \int_M |\alpha|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega \leq \frac{1}{q\varepsilon} \int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega. \end{align*} $$
This type of result was obtained by Inayama (see [Reference Inayama13, Th. 1.3] or [Reference Inayama14, Th. 1.4]). Since the situation is a little bit different, we give a proof for the sake of completeness.
Proof of Theorem 3.1
Fix
![]() $m\in \mathbb {N}$
. Since M is Stein, M can be embedded into
$m\in \mathbb {N}$
. Since M is Stein, M can be embedded into
![]() $\mathbb {C}^N$
for some
$\mathbb {C}^N$
for some
![]() $N>0$
. We may regard M as a closed submanifold in
$N>0$
. We may regard M as a closed submanifold in
![]() $\mathbb {C}^N$
. Let
$\mathbb {C}^N$
. Let
![]() $\iota : M\to \mathbb {C}^N$
be an inclusion map. Thanks to Siu’s theorem [Reference Siu22], there exist an open neighborhood U of M in
$\iota : M\to \mathbb {C}^N$
be an inclusion map. Thanks to Siu’s theorem [Reference Siu22], there exist an open neighborhood U of M in
![]() $\mathbb {C}^N$
and a holomorphic retraction
$\mathbb {C}^N$
and a holomorphic retraction
![]() $p: U\to M$
such that
$p: U\to M$
such that
![]() $p\circ \iota =\mathrm {id}_M$
. Note that
$p\circ \iota =\mathrm {id}_M$
. Note that
![]() $(p^\star E, p^\star h)$
is the trivial vector bundle with a Griffiths semipositive metric
$(p^\star E, p^\star h)$
is the trivial vector bundle with a Griffiths semipositive metric
![]() $p^\star h$
as well. From the results of [Reference Berndtsson and Păun3, Prop. 3.1] and [Reference Raufi21, Prop. 6.2], we obtain a sequence of smooth Hermitian metrics
$p^\star h$
as well. From the results of [Reference Berndtsson and Păun3, Prop. 3.1] and [Reference Raufi21, Prop. 6.2], we obtain a sequence of smooth Hermitian metrics
![]() $\{ g_\nu \}_{\nu =1}^\infty $
with Griffiths semipositive curvature increasing to
$\{ g_\nu \}_{\nu =1}^\infty $
with Griffiths semipositive curvature increasing to
![]() $p^\star h$
on any relatively compact subset in U. Take an exhaustion
$p^\star h$
on any relatively compact subset in U. Take an exhaustion
![]() $\{ M_j\}_{j=1}^\infty $
of M, where each
$\{ M_j\}_{j=1}^\infty $
of M, where each
![]() $M_j$
is a relatively compact Stein subdomain in M,
$M_j$
is a relatively compact Stein subdomain in M,
![]() $M_j\Subset M_{j+1}$
, and
$M_j\Subset M_{j+1}$
, and
![]() $\cup M_j=M$
. Set
$\cup M_j=M$
. Set
![]() $\{ h_\nu := \iota ^\star g_\nu \}_{\nu =1}^\infty $
. Then
$\{ h_\nu := \iota ^\star g_\nu \}_{\nu =1}^\infty $
. Then
![]() $\{ h_\nu \}_{\nu =1}^\infty $
is an approximate sequence with Griffiths semipositive curvature increasing to h on any relatively compact subset. Note that each
$\{ h_\nu \}_{\nu =1}^\infty $
is an approximate sequence with Griffiths semipositive curvature increasing to h on any relatively compact subset. Note that each
![]() $h_\nu $
is Griffiths semipositive. Due to Theorem 2.4,
$h_\nu $
is Griffiths semipositive. Due to Theorem 2.4,
![]() $S^mh_\nu \otimes \det h_\nu $
is Nakano semipositive. The Chern curvature of
$S^mh_\nu \otimes \det h_\nu $
is Nakano semipositive. The Chern curvature of
![]() $S^mh_\nu \otimes \det h_\nu e^{-\psi }$
is calculated as
$S^mh_\nu \otimes \det h_\nu e^{-\psi }$
is calculated as
 $$ \begin{align*} \sqrt{-1} \Theta_{S^mh_\nu \otimes \det h_\nu e^{-\psi}} &=\sqrt{-1} \Theta_{S^mh_\nu \otimes \det h_\nu} + \sqrt{-1} \partial \overline{\partial} \psi\otimes \mathrm{id}_{S^mE\otimes \det E}\\ &\geq_{\mathrm{Nak.}}\varepsilon \omega\otimes \mathrm{id}_{S^mE\otimes \det E}. \end{align*} $$
$$ \begin{align*} \sqrt{-1} \Theta_{S^mh_\nu \otimes \det h_\nu e^{-\psi}} &=\sqrt{-1} \Theta_{S^mh_\nu \otimes \det h_\nu} + \sqrt{-1} \partial \overline{\partial} \psi\otimes \mathrm{id}_{S^mE\otimes \det E}\\ &\geq_{\mathrm{Nak.}}\varepsilon \omega\otimes \mathrm{id}_{S^mE\otimes \det E}. \end{align*} $$
We have that for any
![]() $S^mE\otimes \det E$
-valued
$S^mE\otimes \det E$
-valued
![]() $(n,q)$
-form u,
$(n,q)$
-form u,
Now, we fix
![]() $M_j$
. By using Theorem 2.3 and [Reference Demailly6, Chap. VIII, Rem. 4.8], we get a solution
$M_j$
. By using Theorem 2.3 and [Reference Demailly6, Chap. VIII, Rem. 4.8], we get a solution
![]() $\alpha _\nu $
of the
$\alpha _\nu $
of the
![]() $\overline {\partial }$
-equation satisfying
$\overline {\partial }$
-equation satisfying
 $$ \begin{align*} \int_{M_j}|\alpha_\nu|^2_{\omega, S^mh_\nu\otimes \det h_\nu}e^{-\psi}\mathrm{d}V_\omega &\leq \frac{1}{q\varepsilon}\int_{M_j} |u|^2_{\omega, S^mh_\nu\otimes \det h_\nu}e^{-\psi}\mathrm{d}V_\omega\\ &\leq \frac{1}{q\varepsilon}\int_{M_j} |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega\\ &\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega <+\infty \end{align*} $$
$$ \begin{align*} \int_{M_j}|\alpha_\nu|^2_{\omega, S^mh_\nu\otimes \det h_\nu}e^{-\psi}\mathrm{d}V_\omega &\leq \frac{1}{q\varepsilon}\int_{M_j} |u|^2_{\omega, S^mh_\nu\otimes \det h_\nu}e^{-\psi}\mathrm{d}V_\omega\\ &\leq \frac{1}{q\varepsilon}\int_{M_j} |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega\\ &\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega <+\infty \end{align*} $$
for sufficiently large
![]() $\nu $
. Here, we use the argument from [Reference Khare and Pingali16, Lem. 2.2]. It holds that the metric on
$\nu $
. Here, we use the argument from [Reference Khare and Pingali16, Lem. 2.2]. It holds that the metric on
![]() $S^mE$
induced from E is the same as the metric induced by an orthogonal projection from
$S^mE$
induced from E is the same as the metric induced by an orthogonal projection from
![]() $E^{\otimes m}$
. Hence, by the monotonicity of
$E^{\otimes m}$
. Hence, by the monotonicity of
![]() $h_\nu $
, it follows that
$h_\nu $
, it follows that
![]() $\det h_\nu \leq \det h_{\nu +1}$
,
$\det h_\nu \leq \det h_{\nu +1}$
,
![]() $h_\nu ^{\otimes m}\leq h^{\otimes m}_{\nu +1}$
, and
$h_\nu ^{\otimes m}\leq h^{\otimes m}_{\nu +1}$
, and
![]() $S^mh_\nu \leq S^mh_{\nu +1}$
as a metric.
$S^mh_\nu \leq S^mh_{\nu +1}$
as a metric.
Fix sufficiently large
![]() $\nu _0$
. We have that, for
$\nu _0$
. We have that, for
![]() $\nu \geq \nu _0$
,
$\nu \geq \nu _0$
,
 $$ \begin{align*} \int_{M_j}|\alpha_\nu|^2_{\omega, S^mh_{\nu_0}\otimes \det h_{\nu_0}}e^{-\psi}\mathrm{d}V_\omega &\leq \int_{M_j}|\alpha_\nu|^2_{\omega, S^mh_\nu\otimes \det h_\nu}e^{-\psi}\mathrm{d}V_\omega<+\infty\\ &\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega <+\infty. \end{align*} $$
$$ \begin{align*} \int_{M_j}|\alpha_\nu|^2_{\omega, S^mh_{\nu_0}\otimes \det h_{\nu_0}}e^{-\psi}\mathrm{d}V_\omega &\leq \int_{M_j}|\alpha_\nu|^2_{\omega, S^mh_\nu\otimes \det h_\nu}e^{-\psi}\mathrm{d}V_\omega<+\infty\\ &\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega <+\infty. \end{align*} $$
Then
![]() $\{ \alpha _\nu \}_{\nu \geq \nu _0}$
forms a bounded sequence with respect to the norm
$\{ \alpha _\nu \}_{\nu \geq \nu _0}$
forms a bounded sequence with respect to the norm
![]() $\int _{M_j}|~\cdot ~|^2_{\omega , S^mh_{\nu _0}\otimes \det h_{\nu _0}} e^{-\psi }\mathrm {d}V_\omega $
. We can get a weakly convergent subsequence
$\int _{M_j}|~\cdot ~|^2_{\omega , S^mh_{\nu _0}\otimes \det h_{\nu _0}} e^{-\psi }\mathrm {d}V_\omega $
. We can get a weakly convergent subsequence
![]() $\{ \alpha _{\nu _0, k}\}_k$
. Thus, the weak limit
$\{ \alpha _{\nu _0, k}\}_k$
. Thus, the weak limit
![]() $\alpha _j$
satisfies
$\alpha _j$
satisfies
 $$ \begin{align*} \int_{M_j}|\alpha_j|^2_{\omega, S^mh_{\nu_0}\otimes \det h_{\nu_0}}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega <+\infty. \end{align*} $$
$$ \begin{align*} \int_{M_j}|\alpha_j|^2_{\omega, S^mh_{\nu_0}\otimes \det h_{\nu_0}}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega <+\infty. \end{align*} $$
Next, we fix
![]() $\nu _1> \nu _0$
. Repeating the above argument, we can choose a weakly convergent subsequence
$\nu _1> \nu _0$
. Repeating the above argument, we can choose a weakly convergent subsequence
![]() $\{ \alpha _{\nu _1, k}\}_k \subset \{ \alpha _{\nu _0, k}\}_k$
with respect to
$\{ \alpha _{\nu _1, k}\}_k \subset \{ \alpha _{\nu _0, k}\}_k$
with respect to
![]() $\int _{M_j}|~\cdot ~|^2_{\omega , S^mh_{\nu _1}\otimes \det h_{\nu _1}}e^{-\psi }\mathrm {d}V_\omega $
. Then, by taking a sequence
$\int _{M_j}|~\cdot ~|^2_{\omega , S^mh_{\nu _1}\otimes \det h_{\nu _1}}e^{-\psi }\mathrm {d}V_\omega $
. Then, by taking a sequence
![]() $\{ \nu _n\}_n$
increasing to
$\{ \nu _n\}_n$
increasing to
![]() $+\infty $
and a diagonal sequence, we obtain a weakly convergent sequence
$+\infty $
and a diagonal sequence, we obtain a weakly convergent sequence
![]() $\{ \alpha _{\nu _k, k}\}_k$
with respect to
$\{ \alpha _{\nu _k, k}\}_k$
with respect to
![]() $\int _{M_j}|~\cdot ~|^2_{\omega , S^mh_{\nu _\ell }\otimes \det h_{\nu _\ell }}e^{-\psi }\mathrm {d}V_\omega $
for all
$\int _{M_j}|~\cdot ~|^2_{\omega , S^mh_{\nu _\ell }\otimes \det h_{\nu _\ell }}e^{-\psi }\mathrm {d}V_\omega $
for all
![]() $\ell $
. Hence,
$\ell $
. Hence,
![]() $\alpha _j$
satisfies
$\alpha _j$
satisfies
 $$ \begin{align*} \int_{M_j}|\alpha_j|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega \end{align*} $$
$$ \begin{align*} \int_{M_j}|\alpha_j|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega \end{align*} $$
thanks to the monotone convergence theorem. Since the right-hand side of the above inequality is independent of j, by using the exactly same argument, we can get an
![]() $S^mE\otimes \det E$
-valued
$S^mE\otimes \det E$
-valued
![]() $(n,q-1)$
-form
$(n,q-1)$
-form
![]() $\alpha $
satisfying
$\alpha $
satisfying
![]() $\overline {\partial } \alpha =u$
and
$\overline {\partial } \alpha =u$
and
 $$ \begin{align*} \int_M |\alpha|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega, \end{align*} $$
$$ \begin{align*} \int_M |\alpha|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{q\varepsilon}\int_M |u|^2_{\omega, S^mh\otimes \det h}e^{-\psi}\mathrm{d}V_\omega, \end{align*} $$
which completes the proof.
We call this theorem a singular version of a Demailly–Skoda-type result. Indeed,
![]() $S^mh\otimes \det h$
behaves like a Nakano semipositive metric (cf. Theorem 2.4). Applying this estimate, we can prove the main theorem.
$S^mh\otimes \det h$
behaves like a Nakano semipositive metric (cf. Theorem 2.4). Applying this estimate, we can prove the main theorem.
Proof of Theorem 1.2
We use the same notation as in the previous section and fix
![]() $m\in \mathbb {N}$
. Since the coherence is a local property, we may assume that
$m\in \mathbb {N}$
. Since the coherence is a local property, we may assume that
![]() $X=\Delta ^n_r$
is a polydisc in
$X=\Delta ^n_r$
is a polydisc in
![]() $\mathbb {C}^n_{\{ z_1, \ldots , z_n\}}$
,
$\mathbb {C}^n_{\{ z_1, \ldots , z_n\}}$
,
![]() $E=\Delta ^n_r\times \mathbb {C}^r$
, and
$E=\Delta ^n_r\times \mathbb {C}^r$
, and
![]() $(E=\Delta ^n_r\times \mathbb {C}^r, h)$
is defined over a larger polydisc
$(E=\Delta ^n_r\times \mathbb {C}^r, h)$
is defined over a larger polydisc
![]() $\Delta ^n_{r'}$
. Here, r and
$\Delta ^n_{r'}$
. Here, r and
![]() $r'$
are positive constants satisfying
$r'$
are positive constants satisfying
![]() $r<r'$
, and
$r<r'$
, and
![]() $\Delta ^n_r=\{ (z_1, \ldots , z_n)\in \mathbb {C}^n\mid |z_i|<r \text {for all } i\in \{ 1, \ldots , n\} \}$
. We also assume that
$\Delta ^n_r=\{ (z_1, \ldots , z_n)\in \mathbb {C}^n\mid |z_i|<r \text {for all } i\in \{ 1, \ldots , n\} \}$
. We also assume that
![]() $S^mE$
is trivial over
$S^mE$
is trivial over
![]() $\Delta ^n_{r'}$
. We regard
$\Delta ^n_{r'}$
. We regard
![]() $\log \det h^\star $
as a function on
$\log \det h^\star $
as a function on
![]() $\Delta ^n_{r'}$
which is the local weight of
$\Delta ^n_{r'}$
which is the local weight of
![]() $\det h^\star $
, that is,
$\det h^\star $
, that is,
![]() $\det h^\star |_{\Delta ^n_{r'}}=e^{\log \det h^\star }$
. We can also assume that, on this trivializing coordinate,
$\det h^\star |_{\Delta ^n_{r'}}=e^{\log \det h^\star }$
. We can also assume that, on this trivializing coordinate,
![]() $L(\log \det h^\star )=o$
since the unbounded locus is the set of isolated points.
$L(\log \det h^\star )=o$
since the unbounded locus is the set of isolated points.
Let
![]() $H^0_{2, S^mh}(\Delta ^n_r, S^mE)$
be the space of holomorphic sections s of
$H^0_{2, S^mh}(\Delta ^n_r, S^mE)$
be the space of holomorphic sections s of
![]() $S^mE$
on
$S^mE$
on
![]() $\Delta ^n_r$
such that
$\Delta ^n_r$
such that
![]() $\int _{\Delta ^n_r}|s|^2_{S^mh}\mathrm {d}\lambda <+\infty $
, where
$\int _{\Delta ^n_r}|s|^2_{S^mh}\mathrm {d}\lambda <+\infty $
, where
![]() $\mathrm {d}\lambda $
is the standard Lebesgue measure on
$\mathrm {d}\lambda $
is the standard Lebesgue measure on
![]() $\mathbb {C}^n$
. We consider the natural evaluation map
$\mathbb {C}^n$
. We consider the natural evaluation map
![]() $\mathrm {ev}:H^0_{2, S^mh}(\Delta ^n_r, S^mE)\otimes _{\mathbb {C}}\mathcal {O}_{\Delta ^n_r}\to \mathcal {O}_{\Delta ^n_r}(S^mE)$
. We know that
$\mathrm {ev}:H^0_{2, S^mh}(\Delta ^n_r, S^mE)\otimes _{\mathbb {C}}\mathcal {O}_{\Delta ^n_r}\to \mathcal {O}_{\Delta ^n_r}(S^mE)$
. We know that
![]() $\mathrm {Im}(\mathrm {ev})=:\mathfrak {E}$
is coherent. We now prove that
$\mathrm {Im}(\mathrm {ev})=:\mathfrak {E}$
is coherent. We now prove that
![]() $\mathfrak {E}_x=\mathcal {S}^m\mathcal {E}(S^mh)_x$
for all
$\mathfrak {E}_x=\mathcal {S}^m\mathcal {E}(S^mh)_x$
for all
![]() $x\in \Delta ^n_r$
. Since
$x\in \Delta ^n_r$
. Since
![]() $\mathfrak {E}\subset \mathcal {S}^m\mathcal {E}(S^mh)$
, it is enough to show that
$\mathfrak {E}\subset \mathcal {S}^m\mathcal {E}(S^mh)$
, it is enough to show that
![]() $\mathcal {S}^m\mathcal {E}(S^mh)_x\subset \mathfrak {E}_x$
.
$\mathcal {S}^m\mathcal {E}(S^mh)_x\subset \mathfrak {E}_x$
.
Take an arbitrary element
![]() $f\in \mathcal {S}^m\mathcal {E}(S^mh)_x$
. When
$f\in \mathcal {S}^m\mathcal {E}(S^mh)_x$
. When
![]() $x\neq o$
, we take a cutoff function
$x\neq o$
, we take a cutoff function
![]() $\theta $
around x. Here,
$\theta $
around x. Here,
![]() $\theta $
is a smooth function with compact support such that
$\theta $
is a smooth function with compact support such that
![]() $0\leq \theta \leq 1$
and
$0\leq \theta \leq 1$
and
![]() $\theta \equiv 1$
on an open neighborhood of x. We may assume that f is defined on a small open neighborhood
$\theta \equiv 1$
on an open neighborhood of x. We may assume that f is defined on a small open neighborhood
![]() $U\Subset \Delta ^n_r\setminus \{ o\}$
of x such that
$U\Subset \Delta ^n_r\setminus \{ o\}$
of x such that
![]() $\int _U|f|^2_{S^mh}\mathrm {d}\lambda <+\infty $
and
$\int _U|f|^2_{S^mh}\mathrm {d}\lambda <+\infty $
and
![]() $\mathrm {supp}(\theta )\Subset U$
. Hence,
$\mathrm {supp}(\theta )\Subset U$
. Hence,
![]() $\theta f$
is defined globally. Set
$\theta f$
is defined globally. Set
![]() $u:=\overline {\partial }(\theta f\mathrm {d}z )$
, where
$u:=\overline {\partial }(\theta f\mathrm {d}z )$
, where
![]() $\mathrm {d}z=\mathrm {d}z_1\wedge \cdots \wedge \mathrm {d}z_n$
. Note that
$\mathrm {d}z=\mathrm {d}z_1\wedge \cdots \wedge \mathrm {d}z_n$
. Note that
 $$ \begin{align*} \int_{\Delta^n_r}|u|^2_{S^mh}\mathrm{d}\lambda=\int_U |\overline{\partial} \theta|^2|f|^2_{S^mh}\mathrm{d}\lambda<+\infty. \end{align*} $$
$$ \begin{align*} \int_{\Delta^n_r}|u|^2_{S^mh}\mathrm{d}\lambda=\int_U |\overline{\partial} \theta|^2|f|^2_{S^mh}\mathrm{d}\lambda<+\infty. \end{align*} $$
Moreover, we have that
 $$ \begin{align*} \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\log |z-x|^2-|z|^2}\mathrm{d}\lambda=\int_U |\overline{\partial} \theta|^2|f|^2_{S^mh}e^{-\log \det h^\star -(n+k)\log |z-x|^2- |z|^2}\mathrm{d}\lambda <+\infty \end{align*} $$
$$ \begin{align*} \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\log |z-x|^2-|z|^2}\mathrm{d}\lambda=\int_U |\overline{\partial} \theta|^2|f|^2_{S^mh}e^{-\log \det h^\star -(n+k)\log |z-x|^2- |z|^2}\mathrm{d}\lambda <+\infty \end{align*} $$
for any
![]() $k\in \mathbb {N}$
since
$k\in \mathbb {N}$
since
![]() $\log \det h^\star $
is bounded on U and
$\log \det h^\star $
is bounded on U and
![]() $\overline {\partial }\theta $
is identically zero around x. Set
$\overline {\partial }\theta $
is identically zero around x. Set
![]() $\eta _\delta :=\log (|z-x|^2+\delta ^2)$
and
$\eta _\delta :=\log (|z-x|^2+\delta ^2)$
and
![]() $\eta =\log |z-x|^2$
. We have that
$\eta =\log |z-x|^2$
. We have that
![]() $\sqrt {-1}\partial \overline {\partial }((n+k)\eta _\delta +|z|^2)\geq \sqrt {-1}\sum _i \mathrm {d}z_i\wedge \mathrm {d}\bar {z}_i$
. Applying Theorem 2.3, we get a solution
$\sqrt {-1}\partial \overline {\partial }((n+k)\eta _\delta +|z|^2)\geq \sqrt {-1}\sum _i \mathrm {d}z_i\wedge \mathrm {d}\bar {z}_i$
. Applying Theorem 2.3, we get a solution
![]() $\alpha _\delta $
of
$\alpha _\delta $
of
![]() $\overline {\partial }( \alpha _\delta \mathrm {d}z) =u$
satisfying
$\overline {\partial }( \alpha _\delta \mathrm {d}z) =u$
satisfying
 $$ \begin{align*} \int_{\Delta^n_r}|\alpha_\delta|^2_{S^mh}\det h e^{-(n+k)\eta_\delta-|z|^2}\mathrm{d}\lambda &\leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\eta_\delta-|z|^2}\mathrm{d}\lambda\\ &\leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\eta-|z|^2}\mathrm{d}\lambda<+\infty. \end{align*} $$
$$ \begin{align*} \int_{\Delta^n_r}|\alpha_\delta|^2_{S^mh}\det h e^{-(n+k)\eta_\delta-|z|^2}\mathrm{d}\lambda &\leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\eta_\delta-|z|^2}\mathrm{d}\lambda\\ &\leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\eta-|z|^2}\mathrm{d}\lambda<+\infty. \end{align*} $$
Since the upper bound is independent of
![]() $\delta $
, thanks to the standard
$\delta $
, thanks to the standard
![]() $L^2$
theory of the
$L^2$
theory of the
![]() $\overline {\partial }$
-equation (cf. the proof of Theorem 3.1 or [Reference Hosono and Inayama11, Th. 2.3]), we get a sequence
$\overline {\partial }$
-equation (cf. the proof of Theorem 3.1 or [Reference Hosono and Inayama11, Th. 2.3]), we get a sequence
![]() $\{ \delta _j\}_{j\in \mathbb {N}}$
decreasing to
$\{ \delta _j\}_{j\in \mathbb {N}}$
decreasing to
![]() $0$
, a sequence
$0$
, a sequence
![]() $\{ \alpha _{\delta _j}\}_{j\in \mathbb {N}}$
converging weakly with respect to
$\{ \alpha _{\delta _j}\}_{j\in \mathbb {N}}$
converging weakly with respect to
![]() $S^mh\det he^{-(n+k)\eta _{\delta _j}-|z|^2}$
for all
$S^mh\det he^{-(n+k)\eta _{\delta _j}-|z|^2}$
for all
![]() $j\in \mathbb {N}$
and the limit
$j\in \mathbb {N}$
and the limit
![]() $\alpha $
satisfying
$\alpha $
satisfying
![]() $\overline {\partial } (\alpha \mathrm {d}z)=u$
and
$\overline {\partial } (\alpha \mathrm {d}z)=u$
and
 $$ \begin{align*} \int_{\Delta^n_r}|\alpha|^2_{S^mh}\det h e^{-(n+k)\eta-|z|^2}\mathrm{d}\lambda \leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\eta-|z|^2}\mathrm{d}\lambda. \end{align*} $$
$$ \begin{align*} \int_{\Delta^n_r}|\alpha|^2_{S^mh}\det h e^{-(n+k)\eta-|z|^2}\mathrm{d}\lambda \leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\eta-|z|^2}\mathrm{d}\lambda. \end{align*} $$
Note that
![]() $\log \det h^\star $
,
$\log \det h^\star $
,
![]() $\eta $
, and
$\eta $
, and
![]() $|z|^2$
are bounded above on
$|z|^2$
are bounded above on
![]() $\Delta ^n_r$
. Thus,
$\Delta ^n_r$
. Thus,
 $$ \begin{align*} \int_{\Delta^n_r} |\alpha|^2_{S^mh}\mathrm{d}\lambda<+\infty \text{ and } \int_{\Delta^n_r} \frac{|\alpha|^2_{S^mh}}{|z-x|^{2(n+k)}}\mathrm{d}\lambda<+\infty. \end{align*} $$
$$ \begin{align*} \int_{\Delta^n_r} |\alpha|^2_{S^mh}\mathrm{d}\lambda<+\infty \text{ and } \int_{\Delta^n_r} \frac{|\alpha|^2_{S^mh}}{|z-x|^{2(n+k)}}\mathrm{d}\lambda<+\infty. \end{align*} $$
Then
![]() $\alpha _x\in \mathcal {S}^m\mathcal {E}(S^mh)_x$
. Since
$\alpha _x\in \mathcal {S}^m\mathcal {E}(S^mh)_x$
. Since
![]() $S^mh$
is Griffiths semipositive, there exists a positive constant
$S^mh$
is Griffiths semipositive, there exists a positive constant
![]() $C>0$
such that
$C>0$
such that
![]() $|\alpha |^2_{S^mh} \geq C|\alpha |^2=C(|\alpha _1|^2+\cdots +|\alpha _{r_m}|^2)$
on
$|\alpha |^2_{S^mh} \geq C|\alpha |^2=C(|\alpha _1|^2+\cdots +|\alpha _{r_m}|^2)$
on
![]() $\Delta ^n_r$
, where
$\Delta ^n_r$
, where
![]() $r_m=\mathrm {rank}(S^mE)$
and
$r_m=\mathrm {rank}(S^mE)$
and
![]() $\alpha ={}^t(\alpha _1, \cdots , \alpha _{r_m})$
. Thus,
$\alpha ={}^t(\alpha _1, \cdots , \alpha _{r_m})$
. Thus,
 $$ \begin{align*} \int_{\Delta^n_r} \frac{|\alpha_i|^2}{|z-x|^{2(n+k)}}\mathrm{d}\lambda<+\infty, \end{align*} $$
$$ \begin{align*} \int_{\Delta^n_r} \frac{|\alpha_i|^2}{|z-x|^{2(n+k)}}\mathrm{d}\lambda<+\infty, \end{align*} $$
for each i. Set
![]() $F:=\alpha -\theta f$
. Then
$F:=\alpha -\theta f$
. Then
![]() $F\in H^0_{2, S^mh}(\Delta ^n_r, S^mE)$
and
$F\in H^0_{2, S^mh}(\Delta ^n_r, S^mE)$
and
![]() $\alpha _{i, x}\in \mathfrak {m}_x^{k+1}$
, where
$\alpha _{i, x}\in \mathfrak {m}_x^{k+1}$
, where
![]() $\mathfrak {m}_x$
is the maximal ideal of
$\mathfrak {m}_x$
is the maximal ideal of
![]() $\mathcal {O}_{\Delta ^n_r, x}$
.
$\mathcal {O}_{\Delta ^n_r, x}$
.
When
![]() $x=o$
, the situation changes. Let
$x=o$
, the situation changes. Let
![]() $\theta $
be a cutoff function around the origin, which is identically
$\theta $
be a cutoff function around the origin, which is identically
![]() $1$
around o. Take
$1$
around o. Take
![]() $f\in \mathcal {S}^m\mathcal {E}(S^mh)_o$
, U, and u in the same way. We only need to verify that the following integral is finite:
$f\in \mathcal {S}^m\mathcal {E}(S^mh)_o$
, U, and u in the same way. We only need to verify that the following integral is finite:
 $$ \begin{align*} \int_U |\overline{\partial} \theta|^2|f|^2_{S^mh}e^{-\log \det h^\star -(n+k)\log |z|^2- |z|^2}\mathrm{d}\lambda, \end{align*} $$
$$ \begin{align*} \int_U |\overline{\partial} \theta|^2|f|^2_{S^mh}e^{-\log \det h^\star -(n+k)\log |z|^2- |z|^2}\mathrm{d}\lambda, \end{align*} $$
since
![]() $\log \det h^\star $
is not bounded on U. Note that the support of
$\log \det h^\star $
is not bounded on U. Note that the support of
![]() $\overline {\partial } \theta $
is a compact subset in
$\overline {\partial } \theta $
is a compact subset in
![]() $U\setminus \{ o\}$
. We also see that
$U\setminus \{ o\}$
. We also see that
![]() $\log \det h^\star $
and
$\log \det h^\star $
and
![]() $\log |z|^2$
are bounded on the support of
$\log |z|^2$
are bounded on the support of
![]() $\overline {\partial } \theta $
. Hence, the above integral is finite. Then, repeating the above argument, we get a solution
$\overline {\partial } \theta $
. Hence, the above integral is finite. Then, repeating the above argument, we get a solution
![]() $\alpha $
of
$\alpha $
of
![]() $\overline {\partial } (\alpha \mathrm {d}z)=u$
satisfying
$\overline {\partial } (\alpha \mathrm {d}z)=u$
satisfying
 $$ \begin{align*} \int_{\Delta^n_r}|\alpha|^2_{S^mh}\det h e^{-(n+k)\log |z|^2-|z|^2}\mathrm{d}\lambda \leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\log |z|^2-|z|^2}\mathrm{d}\lambda. \end{align*} $$
$$ \begin{align*} \int_{\Delta^n_r}|\alpha|^2_{S^mh}\det h e^{-(n+k)\log |z|^2-|z|^2}\mathrm{d}\lambda \leq \int_{\Delta^n_r}|u|^2_{S^mh}\det h e^{-(n+k)\log |z|^2-|z|^2}\mathrm{d}\lambda. \end{align*} $$
The rest is the same.
Eventually, in both cases, we obtain that
![]() $\theta f=\alpha -F$
, that is,
$\theta f=\alpha -F$
, that is,
![]() $f_x=\alpha _x-F_x$
for
$f_x=\alpha _x-F_x$
for
![]() $x\in \Delta ^n_r$
. The above argument implies that
$x\in \Delta ^n_r$
. The above argument implies that
![]() $\alpha _x\in \mathfrak {m}_x^{k+1}\cdot \mathcal {O}_{\Delta ^n_r}(S^mE)_x\cap \mathcal {S}^m\mathcal {E}(S^mh)_x$
for all
$\alpha _x\in \mathfrak {m}_x^{k+1}\cdot \mathcal {O}_{\Delta ^n_r}(S^mE)_x\cap \mathcal {S}^m\mathcal {E}(S^mh)_x$
for all
![]() $k\in \mathbb {N}$
. Hence,
$k\in \mathbb {N}$
. Hence,
Thanks to the Artin–Rees lemma, there exists a positive integer
![]() $\ell $
such that, for any
$\ell $
such that, for any
![]() $k\geq \ell -1$
,
$k\geq \ell -1$
,
Thus, for
![]() $k\geq \ell $
,
$k\geq \ell $
,
 $$ \begin{align*} \mathcal{S}^m\mathcal{E}(S^mh)_x&=\mathfrak{m}_x^{k+1}\cdot \mathcal{O}_{\Delta^n_r}(S^mE)_x\cap \mathcal{S}^m\mathcal{E}(S^mh)_x+ \mathfrak{E}_x\\ &=\mathfrak{m}_x^{k-\ell+1}(\mathfrak{m}_x^{\ell}\cdot \mathcal{O}_{\Delta^n_r}(S^mE)_x\cap \mathcal{S}^m\mathcal{E}(S^mh)_x)+ \mathfrak{E}_x\\ &\subset \mathfrak{m}_x \cdot\mathcal{S}^m\mathcal{E}(S^mh)_x+ \mathfrak{E}_x\\ &\subset \mathcal{S}^m\mathcal{E}(S^mh)_x. \end{align*} $$
$$ \begin{align*} \mathcal{S}^m\mathcal{E}(S^mh)_x&=\mathfrak{m}_x^{k+1}\cdot \mathcal{O}_{\Delta^n_r}(S^mE)_x\cap \mathcal{S}^m\mathcal{E}(S^mh)_x+ \mathfrak{E}_x\\ &=\mathfrak{m}_x^{k-\ell+1}(\mathfrak{m}_x^{\ell}\cdot \mathcal{O}_{\Delta^n_r}(S^mE)_x\cap \mathcal{S}^m\mathcal{E}(S^mh)_x)+ \mathfrak{E}_x\\ &\subset \mathfrak{m}_x \cdot\mathcal{S}^m\mathcal{E}(S^mh)_x+ \mathfrak{E}_x\\ &\subset \mathcal{S}^m\mathcal{E}(S^mh)_x. \end{align*} $$
Nakayama’s lemma says that
![]() $\mathcal {S}^m\mathcal {E}(S^mh)_x=\mathfrak {E}_x$
, which completes the proof.
$\mathcal {S}^m\mathcal {E}(S^mh)_x=\mathfrak {E}_x$
, which completes the proof.
We then give a proof of Corollary 1.3 as an application of the main theorem.
Proof of Corollary 1.3
First, we prove that
![]() $\det h$
is radial if h is spherically symmetric. Since
$\det h$
is radial if h is spherically symmetric. Since
![]() $E=\mathbb {B}^n\times \mathbb {C}^r$
is trivial, taking a global holomorphic frame, we write
$E=\mathbb {B}^n\times \mathbb {C}^r$
is trivial, taking a global holomorphic frame, we write
![]() $h=(h_{i\bar {j}})_{1\leq i,j\leq r}$
. Akin to [Reference Păun and Takayama20], we compute each element
$h=(h_{i\bar {j}})_{1\leq i,j\leq r}$
. Akin to [Reference Păun and Takayama20], we compute each element
![]() $h_{i\bar {j}}$
. For
$h_{i\bar {j}}$
. For
![]() $v_1={}^t(1, 0, \ldots , 0)$
,
$v_1={}^t(1, 0, \ldots , 0)$
,
![]() $|v_1|^2_h=h_{1\bar {1}}$
is a radial plurisubharmonic function with
$|v_1|^2_h=h_{1\bar {1}}$
is a radial plurisubharmonic function with
![]() $h_{1\bar {1}}(z)\in [0, +\infty )$
. We also have that
$h_{1\bar {1}}(z)\in [0, +\infty )$
. We also have that
![]() $|v_2|_h=h_{2\bar {2}}$
is a radial plurisubharmonic function for
$|v_2|_h=h_{2\bar {2}}$
is a radial plurisubharmonic function for
![]() $v_2={}^t(0,1,0,\ldots ,0)$
. For
$v_2={}^t(0,1,0,\ldots ,0)$
. For
![]() $v={}^t(1,1,0,\ldots , 0)$
and
$v={}^t(1,1,0,\ldots , 0)$
and
![]() $v'={}^t(1,\sqrt {-1},0,\ldots ,0)$
, we get
$v'={}^t(1,\sqrt {-1},0,\ldots ,0)$
, we get
![]() $|v|^2_h=h_{1\bar {1}}+h_{2\bar {2}}+2\mathrm {Re}(h_{1\bar {2}})$
and
$|v|^2_h=h_{1\bar {1}}+h_{2\bar {2}}+2\mathrm {Re}(h_{1\bar {2}})$
and
![]() $|v'|^2_{h}=h_{1\bar {1}}+h_{2\bar {2}}-2\mathrm {Im}(h_{1\bar {2}})$
, respectively. We have that
$|v'|^2_{h}=h_{1\bar {1}}+h_{2\bar {2}}-2\mathrm {Im}(h_{1\bar {2}})$
, respectively. We have that
![]() $|v|^2_h$
and
$|v|^2_h$
and
![]() $|v'|^2_h$
are also radial due to the assumption of h. Thus,
$|v'|^2_h$
are also radial due to the assumption of h. Thus,
![]() $h_{1\bar {2}}$
is spherically symmetric. Consequently, we can say that every element
$h_{1\bar {2}}$
is spherically symmetric. Consequently, we can say that every element
![]() $h_{i\bar {j}}$
is spherically symmetric, and so is
$h_{i\bar {j}}$
is spherically symmetric, and so is
![]() $\log \det h$
.
$\log \det h$
.
Therefore, it is enough to give a proof in the case that
![]() $\log \det h$
is a radial plurisubharmonic function. The rest part follows due to the standard argument below (cf. [Reference Demailly6, Chap. I, §5]). Set
$\log \det h$
is a radial plurisubharmonic function. The rest part follows due to the standard argument below (cf. [Reference Demailly6, Chap. I, §5]). Set
![]() $H:=\{ w\in \mathbb {C} \mid \mathrm {Re}(w)<0 \}$
. Define the map
$H:=\{ w\in \mathbb {C} \mid \mathrm {Re}(w)<0 \}$
. Define the map
![]() $\exp :H\to \mathbb {B}^n\setminus \{o\}$
by
$\exp :H\to \mathbb {B}^n\setminus \{o\}$
by
![]() $w\mapsto (e^{w},0, \ldots , 0)$
. Then
$w\mapsto (e^{w},0, \ldots , 0)$
. Then
![]() $\log \det h \circ \exp $
is a plurisubharmonic function on H, which is independent of
$\log \det h \circ \exp $
is a plurisubharmonic function on H, which is independent of
![]() $\mathrm {Im}(w)$
. Thus,
$\mathrm {Im}(w)$
. Thus,
![]() $x\in (-\infty , 0)\mapsto \log \det h(e^{x},0,\ldots ,0)$
is a convex function. We denote this map by
$x\in (-\infty , 0)\mapsto \log \det h(e^{x},0,\ldots ,0)$
is a convex function. We denote this map by
![]() $\mu $
. We then have that
$\mu $
. We then have that
![]() $\log \det h(z)=\mu (\log |z|)$
for
$\log \det h(z)=\mu (\log |z|)$
for
![]() $z\in \mathbb {B}^n\setminus \{ o\}$
. We can conclude that
$z\in \mathbb {B}^n\setminus \{ o\}$
. We can conclude that
![]() $L(\log \det h)\subset \{ o\}$
. Since the unbounded locus
$L(\log \det h)\subset \{ o\}$
. Since the unbounded locus
![]() $L(\det h)$
of
$L(\det h)$
of
![]() $\det h$
is isolated or empty, this corollary holds.
$\det h$
is isolated or empty, this corollary holds.
At the last of this section, we introduce an example satisfying the condition in Corollary 1.3. This type of example was introduced in [Reference Inayama12].
Example 3.2. Let h be a singular Hermitian metric on
![]() $E=\mathbb {B}^n\times \mathbb {C}^2$
defined by
$E=\mathbb {B}^n\times \mathbb {C}^2$
defined by
 $$ \begin{align*} h= \left(\kern-4pt \begin{array}{cc} |z_1|^2 + |z|^{N} & z_1 \\ \overline{z}_1 & 1 \end{array}\kern-6pt \right) \end{align*} $$
$$ \begin{align*} h= \left(\kern-4pt \begin{array}{cc} |z_1|^2 + |z|^{N} & z_1 \\ \overline{z}_1 & 1 \end{array}\kern-6pt \right) \end{align*} $$
for sufficiently large
![]() $N>0$
. Then h is Griffiths seminegative since for any local holomorphic section
$N>0$
. Then h is Griffiths seminegative since for any local holomorphic section
![]() $u={}^t(u_1, u_2)$
,
$u={}^t(u_1, u_2)$
,
We have that
![]() $\det h=|z|^N$
. Thus,
$\det h=|z|^N$
. Thus,
![]() $\mathcal {S}^m\mathcal {E}^\star (S^mh^\star )$
is coherent for every
$\mathcal {S}^m\mathcal {E}^\star (S^mh^\star )$
is coherent for every
![]() $m\in \mathbb {N}$
thanks to Corollary 1.3. Note that
$m\in \mathbb {N}$
thanks to Corollary 1.3. Note that
![]() $\mathcal {E}^\star (h^\star )\neq \mathcal {O}_{\mathbb {B}^2}(E^\star )$
due to the assumption of N.
$\mathcal {E}^\star (h^\star )\neq \mathcal {O}_{\mathbb {B}^2}(E^\star )$
due to the assumption of N.
Acknowledgment
Takahiro Inayama would like to thank Prof. Shin-ichi Matsumura and Dr. Genki Hosono for valuable discussions and helpful comments.
Appendix. On Riemann surfaces
In this appendix, we discuss singular Hermitian metrics on a holomorphic vector bundle over a Riemann surface. If
![]() $\dim X=1$
, the situation is quite different. Actually, on Riemann surfaces, Griffiths positivity is equivalent to Nakano positivity by definition. Repeating the argument in the proof of Theorem 3.1, we have the following result.
$\dim X=1$
, the situation is quite different. Actually, on Riemann surfaces, Griffiths positivity is equivalent to Nakano positivity by definition. Repeating the argument in the proof of Theorem 3.1, we have the following result.
Theorem A.1 (cf. [Reference Inayama14, Prop. 5.2]).
Let
![]() $(M, \omega )$
be a noncompact Riemann surface. We also let
$(M, \omega )$
be a noncompact Riemann surface. We also let
![]() $(E=M\times \mathbb {C}^r, h)$
be the trivial vector bundle with a Griffiths semipositive singular Hermitian metric, and let
$(E=M\times \mathbb {C}^r, h)$
be the trivial vector bundle with a Griffiths semipositive singular Hermitian metric, and let
![]() $\psi $
be a smooth strictly plurisubharmonic function with
$\psi $
be a smooth strictly plurisubharmonic function with
![]() $\sqrt {-1}\partial \overline {\partial } \psi \geq \varepsilon \omega $
for some positive constant
$\sqrt {-1}\partial \overline {\partial } \psi \geq \varepsilon \omega $
for some positive constant
![]() $\varepsilon>0$
. Then, for any E-valued
$\varepsilon>0$
. Then, for any E-valued
![]() $(1,1)$
-form u with finite
$(1,1)$
-form u with finite
![]() $L^2$
-norm, there exists an E-valued
$L^2$
-norm, there exists an E-valued
![]() $(1,0)$
-form
$(1,0)$
-form
![]() $\alpha $
such that
$\alpha $
such that
![]() $\overline {\partial } \alpha =u$
and
$\overline {\partial } \alpha =u$
and
 $$ \begin{align*} \int_M |\alpha|^2_{\omega,h}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{\varepsilon}\int_M |u|^2_{\omega,h}e^{-\psi}\mathrm{d}V_\omega. \end{align*} $$
$$ \begin{align*} \int_M |\alpha|^2_{\omega,h}e^{-\psi}\mathrm{d}V_\omega\leq \frac{1}{\varepsilon}\int_M |u|^2_{\omega,h}e^{-\psi}\mathrm{d}V_\omega. \end{align*} $$
This
![]() $L^2$
-estimate immediately implies the following theorem.
$L^2$
-estimate immediately implies the following theorem.
Theorem A.2. Let
![]() $(E,h)\to S$
be a holomorphic vector bundle with a Griffiths semipositive singular Hermitian metric h over a Riemann surface S. Then
$(E,h)\to S$
be a holomorphic vector bundle with a Griffiths semipositive singular Hermitian metric h over a Riemann surface S. Then
![]() $\mathcal {E}(h)$
is coherent.
$\mathcal {E}(h)$
is coherent.
This theorem may be already known for some experts. However, to emphasize the case that
![]() $\dim X=1$
is special, we want to note the above result explicitly.
$\dim X=1$
is special, we want to note the above result explicitly.