1 Introduction
1.1 A wug-shaped curve
Traditional generative theories of linguistics tend to focus on categorical generalisations, assuming that the grammar makes only dichotomous distinctions between grammatical and ungrammatical forms. This assumption is often made clear in syntactic research in which the grammaticality distinction is taken to be binary (e.g. Chomsky Reference Chomsky1957, Schütze Reference Schütze1996, Sprouse Reference Sprouse2007). The same approach is apparent in early work in generative phonological research, in which the crucial distinction is between impossible forms (e.g. bnick) and possible/existing forms (e.g. brick or blick) (Chomsky & Halle Reference Chomsky and Halle1968, Halle Reference Halle, Halle, Bresnan and Miller1978). Probabilistic or stochastic generalisations were rarely the focus of formal phonological analyses, although, in practice, exceptions to phonological generalisations were usually acknowledged, and handled by some means (e.g. Kisseberth Reference Kisseberth1970).
On the other hand, probabilistic generalisations regarding phonological variations have been a central topic of sociolinguistic research (e.g. Labov Reference Labov1966, Guy Reference Guy2011), in which it has been claimed that variation is ‘the central problem of linguistics’ (Labov Reference Labov, Ammon, Dittmar, Mattheier and Trudgill2004: 6). For example, it is not uncommon for the same word to be produced differently in different social or discourse contexts. Some phonological processes can apply with different probabilities in different contexts, and these probabilities can be predicted on the basis of the interaction of various (morpho-)phonological and social factors (e.g. t/d-deletion in English: Guy Reference Guy1991), an observation which has been modelled in various formal frameworks (e.g. Cedergren & Sankoff Reference Cedergren and Sankoff1974, Guy Reference Guy1991, Johnson Reference Johnson2009). Syntactic variations and their historical changes also seem to exhibit systematic quantitative patterns (Kroch Reference Kroch1989, Zimmermann Reference Zimmermann2017); these have also been analysed from formal perspectives (e.g. Featherston Reference Featherston, Kepser and Reis2005, Bresnan & Hay Reference Bresnan and Hay2008).
In harmony with these views, a growing body of recent studies has shown that phonological knowledge is deeply stochastic in nature (e.g. Boersma & Hayes Reference Boersma and Hayes2001, Pierrehumbert Reference Pierrehumbert2001, Cohn Reference Cohn, Fanselow, Féry, Vogel and Schlesewsky2006, Hayes & Londe Reference Hayes and Londe2006, Coetzee & Pater Reference Coetzee, Pater, Goldsmith, Riggle and Yu2011, Daland et al. Reference Daland, Hayes, White, Garellek, Davis and Norrmann2011). Some phonotactic sequences are neither completely grammatical nor ungrammatical, but intermediate; indeed, controlled phonotactic judgement experiments typically reveal a continuous gradient pattern (e.g. Daland et al. Reference Daland, Hayes, White, Garellek, Davis and Norrmann2011).
The field of phonology has recently witnessed a rise of interest in formal grammatical models which can account for such stochastic phonological generalisations. Among these, the three most widely employed frameworks are (i) Stochastic Optimality Theory (Boersma Reference Boersma1998, Boersma & Hayes Reference Boersma and Hayes2001), (ii) Noisy Harmonic Grammar (Coetzee & Kawahara Reference Coetzee and Kawahara2013, Boersma & Pater Reference Boersma, Pater, McCarthy and Pater2016, Hayes Reference Hayes2017) and (iii) Maximum Entropy Harmonic Grammar (henceforth MaxEnt) (Goldwater & Johnson Reference Goldwater, Johnson, Spenader, Eriksson and Dahl2003, Zuraw & Hayes Reference Zuraw and Hayes2017). How these stochastic models of phonology should be teased apart is currently a topic of debate in phonological studies (Jäger & Rosenbach Reference Jäger and Rosenbach2006, Jäger Reference Jäger, Zaenen, Simpson, King, Grimshaw, Maling and Manning2007, Hayes Reference Hayes2017, Reference Hayes2020, Zuraw & Hayes Reference Zuraw and Hayes2017, Anttila & Magri Reference Anttila and Magri2018, Breiss Reference Breiss2020, among many others).
In order to distinguish between these theoretical frameworks, Hayes (Reference Hayes2020), building upon a body of previous studies on probabilistic linguistic patterns (Kroch Reference Kroch1989, McPherson & Hayes Reference McPherson and Hayes2016, Zimmermann Reference Zimmermann2017, Zuraw & Hayes Reference Zuraw and Hayes2017), proposes an abstract, top-down approach, asking the following question: if we take the MaxEnt grammar framework seriously, what predictions does it make for its quantitative signature, i.e. the probabilistic pattern that it typically generates? More specifically, suppose that there is a scalar constraint, S, that is gradiently violable – i.e. its violations can be assessed on a numerical scale – and a binary constraint, B.Footnote 1 Further suppose that these constraints are in direct conflict with each other; i.e. the satisfaction of S entails the violation B, and vice versa. When we simulate the probabilities of the candidate that obeys B and violates S as a function of the number of violations of S, we get a sigmoid (s-shaped) curve, as shown in Fig. 1. In reality, the constraint-violation profile of S is discrete (ranging from 1 to 7 in Fig. 1), but for the sake of illustration, Fig. 1 continuously plots for all values, not just the integers. This curve is characterised by the fact that the y-axis values do not change very much when the x-axis values are small (from 1 to 3) or large (from 5 to 7), but display radical change in the middle range (from 3 to 5).

Figure 1 A sigmoid curve predicted by the MaxEnt grammar with a scalar constraint S and a binary constraint B, whose violations conflict. Based on Hayes (2020: 5). The mathematical equation which derives this curve is y = 1 / (1+e −H), where H directly correlates with the number of violations of S. See Jurafsky & Martin (2019) and McPherson & Hayes (2016), as well as §5.1.
Hayes also considers a case in which two sets of inputs are relevant – each set consists of outputs with the constraint-violation profiles that are identical to those in Fig. 1, but the two sets differ in terms of whether they violate an additional ‘perturber’ constraint (P) or not. This scenario creates two identical sigmoid curves, shifted from one another on the horizontal axis, as in Fig. 2a. Hayes (Reference Hayes2020) calls these ‘wug-shaped curves’, because, as illustrated in Fig. 2b, they are reminiscent of the beloved animal familiar to the general linguistic community since the classic work of Berko (Reference Berko1958).

Figure 2 Wug-shaped curves with two sigmoid functions. Adapted from Hayes (2020: 7).
Studying whether wug-shaped curves are observed in linguistic patterns is important, because they are natural outcomes of MaxEnt grammars, and are also predicted under some versions of Noisy Harmonic Grammar, but not in Stochastic Optimality Theory. This top-down approach to examining quantitative signatures of linguistic generalisations therefore offers a possible strategy for distinguishing among three competing stochastic models of grammar. If we find wug-shaped curves in linguistic patterns, this provides support for MaxEnt or Noisy Harmonic Grammar over Stochastic Optimality Theory. Hayes (Reference Hayes2020), building upon McPherson & Hayes (Reference McPherson and Hayes2016) and Zuraw & Hayes (Reference Zuraw and Hayes2017), argues that such wug-shaped curves are commonly observed in probabilistic phonology, as well as in other domains of linguistic patterns, such as categorical perception of speech sounds (Liberman et al. Reference Liberman, Harris, Hoffman and Griffith1957) and diachronic changes in syntax (Kroch Reference Kroch1989, Zimmermann Reference Zimmermann2017).
Building on these studies, this paper asks whether we can identify wug-shaped curves in the patterns of sound symbolism, i.e. systematic/iconic associations between sounds and meanings (Hinton et al. Reference Hinton, Nichols and Ohala2006). If the answer to this question turns out to be positive, this provides support for the idea that MaxEnt is suited to model the knowledge that lies behind sound symbolism (Kawahara et al. Reference Kawahara, Katsuda and Kumagai2019, Kawahara Reference Kawahara2020a). Moreover, to the extent that MaxEnt is appropriate as a model of phonological knowledge (Hayes & Wilson Reference Hayes and Wilson2008, McPherson & Hayes Reference McPherson and Hayes2016, Zuraw & Hayes Reference Zuraw and Hayes2017, among many others), it implies that the same mechanism may lie behind phonological patterns and sound-symbolic patterns; i.e. that there is a non-trivial parallel between phonological patterns and sound-symbolic patterns.
1.2 Cumulativity
One general theoretical issue that lies behind wug-shaped curves is that of cumulativity. This is a topic that has been addressed in recent linguistic theorisation, because it potentially helps us to distinguish Optimality Theory with ranked constraints (Prince & Smolensky Reference Prince and Smolensky1993) from constraint-based theories with numerically weighted constraints, such as Harmonic Grammar (Jäger & Rosenbach Reference Jäger and Rosenbach2006, Jäger Reference Jäger, Zaenen, Simpson, King, Grimshaw, Maling and Manning2007, Pater Reference Pater2009, Potts et al. Reference Potts, Pater, Jesney, Bhatt and Becker2010, Hayes et al. Reference Hayes, Wilson and Shisko2012, McPherson & Hayes Reference McPherson and Hayes2016, Zuraw & Hayes Reference Zuraw and Hayes2017, Breiss Reference Breiss2020).
It is convenient to distinguish two types of cumulativity, counting cumulativity and ganging-up cumulativity (Jäger & Rosenbach Reference Jäger and Rosenbach2006, Jäger Reference Jäger, Zaenen, Simpson, King, Grimshaw, Maling and Manning2007), because they present different types of challenges to Optimality Theory. In the context of OT, we find counting cumulativity when two or more violations of a lower-ranked constraint take precedence over the violation of a higher-ranked constraint. Consider the schematic case of counting cumulativity in (1a). As (1a.i) shows, Constraint A dominates Constraint B. However, as in (1a.ii), two violations of Constraint B are considered to be more important than a single violation of Constraint A.
If Constraint A dominates Constraint B in an OT analysis, then a single violation of Constraint A should take precedence over any number of violations of Constraint B – this is a consequence of the strict domination of constraint rankings, a central tenet of OT (Prince & Smolensky Reference Prince and Smolensky1993). In reality, however, it is not uncommon for a language to tolerate one violation of a particular constraint, but not two violations, instantiating a case of counting cumulativity. For instance, the native phonology of Japanese allows one voiced obstruent within a morpheme, but not two (Lyman's Law; Itô & Mester Reference Itô and Mester1986, Reference Ito and Mester2003). Such observations are commonly accounted for in OT by positing OCP constraints (Leben Reference Leben1973, Itô & Mester Reference Itô and Mester1986, Myers Reference Myers1997) or self-conjoined constraints, which are violated if and only if there are two instances of the same structure (Alderete Reference Alderete1997, Ito & Mester Reference Ito and Mester2003). Grammatical frameworks related to OT, which use numerical weights instead of rankings, can account for counting cumulativity without positing any additional mechanism (e.g. McPherson & Hayes Reference McPherson and Hayes2016).Footnote 2
-
(1)

Ganging-up cumulativity is illustrated by the set of tableaux in (1b). In (1b.i) and (1b.ii) Constraint A dominates Constraint B and Constraint C respectively. Ganging-up cumulativity is said to hold when the simultaneous violation of Constraint B and Constraint C takes precedence over a single violation of Constraint A, as in (1b.iii); i.e. violations of Constraint B and Constraint C ‘gang up’ to take precedence over a violation of Constraint A. To analyse a ganging-up cumulativity pattern, OT generally requires local conjunction of Constraints B and C (Smolensky Reference Smolensky1995, Crowhurst Reference Crowhurst2011). For example, the loanword phonology of Japanese tolerates voiced obstruent geminates in isolation, as well as two voiced obstruent singletons. However, voiced obstruent geminates undergo devoicing when they co-occur with another voiced obstruent. In order to account for this pattern, Nishimura (Reference Nishimura2006) proposes the local conjunction of *VoicedObsGem and OCP[voice] within the stem domain. Frameworks with numerically weighted constraints can account for this ganging-up cumulativity pattern in Japanese without stipulating a complex locally conjoined constraint (Pater Reference Pater2009; see also Potts et al. Reference Potts, Pater, Jesney, Bhatt and Becker2010).
In short, whether phonological patterns show counting or ganging-up cumulativity bears on the issue of whether the grammatical model should be based on rankings or weights. More generally, the question is whether the optimisation algorithm deployed in the linguistic system is based on lexicographic ordering or numeric ordering (Tesar Reference Tesar2007).
In this paper I attempt to shed new light on this debate by examining a pattern that has hitherto hardly been analysed from this perspective, namely, sound symbolism. The primary question that is addressed in this study is whether sound symbolism shows counting cumulativity effects and/or ganging-up cumulativity effects, and if so, how.
This is an empirical question that is important to address for its own sake, because only a few studies have directly considered the (non-)cumulative nature of sound symbolism, and this is one aspect of sound symbolism that is only poorly understood. There are some impressionistic reports regarding counting cumulativity in the literature which suggest that more segments of the same kind evoke stronger sound-symbolic images (e.g. Martin Reference Martin and Poppe1962, McCarthy Reference McCarthy, Richardson, Marks and Chukerman1983, Hamano Reference Hamano, Shinohara and Uno2013). Thompson & Estes (Reference Thompson and Estes2011) carried out experiments to establish whether sound symbolism is categorical or gradient, and found some evidence for cumulativity in their results. A recent experimental study by Kawahara & Kumagai (Reference Kawahara and Kumagaito appear) found evidence for counting cumulativity in various sound-symbolic values of voiced obstruents in Japanese. D'Onofrio (Reference D'Onofrio2014) examined the bouba-kiki effect (Ramachandran & Hubbard Reference Ramachandran and Hubbard2001), in which certain classes of sounds are associated with round figures and other classes with angular figures. She found that vowel backness, consonant voicing and consonant labiality all contribute to the perception of roundness, instantiating a case of ganging-up cumulativity.Footnote 3 To the best of my knowledge, there have been no studies that have addressed the question of whether counting cumulativity and ganging-up cumulativity can coexist in the same sound-symbolic system, as predicted by MaxEnt (though see Kawahara, Suzuki & Kumagai Reference Kawahara, Suzuki and Kumagai2020, which is discussed in some detail in §2).
In a sense, this question – whether the same pattern can show counting cumulativity and ganging-up cumulativity at the same time – is the one addressed by Hayes (Reference Hayes2020): each of the two sigmoid curves in a wug-shaped curve can arise when there is counting cumulativity, and the separation between the two curves is a sign of ganging-up cumulativity. It is important to note, however, that cumulativity is a necessary, but not sufficient, condition for a wug-shaped curve. A sigmoid curve, a crucial component of a wug-shaped curve, entails counting cumulativity, but not vice versa. Counting cumulativity, for example, can be manifested as a linear function, rather than a sigmoid function. See §5.3 for further elaboration on this point.
In domains other than sound symbolism, Breiss (Reference Breiss2020) shows that we observe both counting and ganging-up cumulativity in phonotactic learning patterns in an artificial language learning experiment. Case studies of phonological alternation patterns reported in McPherson & Hayes (Reference McPherson and Hayes2016) and Zuraw & Hayes (Reference Zuraw and Hayes2017) can also be understood as simultaneously involving counting and ganging-up cumulativity. There have not been many other case studies that have directly addressed this question, especially in the domain of sound symbolism. Since the coexistence of counting cumulativity and ganging-up cumulativity is a natural consequence of MaxEnt, one aim of this paper is to address this gap in the literature.
The issue of cumulativity in sound symbolism is interesting to address from a more general theoretical perspective as well. To the extent that cumulativity is a general property of phonological patterns (McPherson & Hayes Reference McPherson and Hayes2016, Zuraw & Hayes Reference Zuraw and Hayes2017, Breiss Reference Breiss2020, Hayes Reference Hayes2020), and if sound-symbolic effects show similar cumulative properties, then we may conclude that there exists a non-trivial parallel between phonological patterns and sound-symbolic patterns (Kawahara Reference Kawahara2020a). This parallel would lend some credibility to the hypothesis that sound symbolism is a part of ‘core’ linguistic knowledge, as has recently been argued (Alderete & Kochetov Reference Alderete and Kochetov2017, Kumagai Reference Kumagai2019, Jang Reference Jang2020, Kawahara Reference Kawahara2020a, b, Shih Reference Shih2020). This is a rather radical conclusion, given the fact that sound symbolism has long been considered as being outside the purview of theoretical linguistics.
1.3 Pokémonastics
In addition to addressing the issue of cumulativity in sound symbolism, this study can also be considered as a case study of the Pokémonastics research paradigm, within which researchers explore the nature of sound symbolism using Pokémon names (Kawahara et al. Reference Kawahara, Noto and Kumagai2018, Shih et al. Reference Shih, Ackerman, Hermalin, Inkelas, Jang, Johnson, Kavitskaya, Kawahara, Oh, Starr and Yu2019). I refer the readers to Shih et al. (Reference Shih, Ackerman, Hermalin, Inkelas, Jang, Johnson, Kavitskaya, Kawahara, Oh, Starr and Yu2019) for discussion of this research paradigm, and provide minimal background information necessary for what follows.
Pokémon is a game series which was first released by Nintendo Inc. in 1996, and has become very popular worldwide. In this game series, players collect and train fictional creatures called Pokémons (Pokémon is a truncation of poketto monsutaa ‘pocket monster’). One feature that will be crucial in what follows is that some Pokémon characters undergo evolution, and when they do so, they generally become larger, heavier and stronger. When they evolve, moreover, they acquire a different name: for instance, Iwaaku becomes Haganeeru.
Kawahara et al. (Reference Kawahara, Noto and Kumagai2018) show that when we systematically examine their names from the perspectives of sound symbolism, post-evolution characters have longer names than pre-evolution characters. They attribute this observation to a previously formulated sound-symbolic principle, ‘the iconicity of quantity’ (Haiman Reference Haiman1980, Reference Haiman1984), in which larger quantity is expressed by longer phonological material. They also show that post-evolution Pokémon characters are more likely than pre-evolution characters to have names with voiced obstruents. This is likely to be related to the observation that Japanese voiced obstruents often sound-symbolically denote large quantity and/or strength (Hamano Reference Hamano1998, Kawahara Reference Kawahara2017). Both of these sound-symbolic effects can be seen in the pair Iwaaku vs. Haganeeru: evolved Haganeeru has five moras and contains a voiced obstruent [g], while unevolved Iwaaku has only four moras and no voiced obstruents. The experiment below examines these two sound-symbolic effects in further detail.
The rest of this paper proceeds as follows. §2 reports the methods of the experiment, which was designed to address the question of whether we observe a wug-shaped curve in sound symbolism. The results of the experiment demonstrate that sound symbolism shows both counting and ganging-up cumulativity, and that these two types of cumulativity can coexist within a single sound-symbolic system (§3 and §4). These cumulative patterns result in a wug-shaped curve, which can naturally be modelled using MaxEnt (§5). §6 discusses several attempts to use Stochastic OT to model the current results, which shows that this framework requires additional tweaks to fit the wug-shaped pattern observed in the experiment. §7 offers concluding remarks, arguing that formal phonology and research on sound symbolism can inform one another.
2 Methods
One precursor of the current experiment is Kawahara, Suzuki & Kumagai (Reference Kawahara, Suzuki and Kumagai2020), who carried out a judgement experiment on the strengths of Pokémon move names (moves are what Pokémons use when they battle with each other). Kawahara, Suzuki & Kumagai manipulated mora count from two to seven moras, and showed that the longer the nonce names, the stronger they were judged to be. They also manipulated the presence/absence of a voiced obstruent in word-initial position, and found that nonce move names with voiced obstruents were judged to be stronger. Their results are reproduced in Fig. 3, which instantiates both counting cumulativity (the effect of mora count) and ganging-up cumulativity (the additive effects of the two factors). However, their experiment is not suitable for addressing the question of whether we observe wug-shaped curves in sound symbolism, nor were their results amenable to a MaxEnt analysis, because the judged values were continuous – what we need instead is the probability distributions of categorical outcomes.

Figure 3 The effects of mora count and word-initial voiced obstruents on judged attack values in nonce Pokémon move names. The y-axis shows standardised judged attack values, which are continuous. Adapted from Kawahara, Suzuki & Kumagai (2020: Fig. 4).
The current study builds upon Kawahara, Suzuki & Kumagai (Reference Kawahara, Suzuki and Kumagai2020), but in order to obtain a binary categorical response, participants in the experiment were asked to judge whether each stimulus name was better suited for a pre-evolution or post-evolution character. To obtain more reliable estimates of each condition, more items were included for each condition. Moreover, in this study responses were collected from many more participants.
2.1 Stimuli
The stimuli used in the experiment are listed in Table I. Building on the two studies reviewed above (Kawahara et al. Reference Kawahara, Noto and Kumagai2018, Kawahara, Suzuki & Kumagai Reference Kawahara, Suzuki and Kumagai2020), two variables were manipulated: mora count and the presence of a voiced obstruent in word-initial position. The mora count was varied, in order to investigate counting cumulativity and, relatedly, to examine whether varying the mora count would result in a sigmoid curve. Mora counts varied from two to six, corresponding to minimum and maximum lengths for Pokémon names. The experiment manipulated mora counts rather than segment or syllable counts, because mora counts were identified as most important in the previous studies (Kawahara et al. Reference Kawahara, Noto and Kumagai2018, Shih et al. Reference Shih, Ackerman, Hermalin, Inkelas, Jang, Johnson, Kavitskaya, Kawahara, Oh, Starr and Yu2019, Kawahara, Suzuki & Kumagai Reference Kawahara, Suzuki and Kumagai2020); moreover, the mora is the most psycholinguistically salient prosodic counting unit in Japanese (Otake et al. Reference Otake, Hatano, Cutler and Mehler1993). The perturbing factor (see §1.1) was the presence or absence of a voiced obstruent in name-initial position.
Table I The stimuli used in the experiment. Mora boundaries are represented as dots.

As shown in Table I, there were six items in each cell. All the names were created using a nonce-name generator, which randomly combines Japanese moras to create new names.Footnote 4 This random generator was used to preclude potential bias by the experimenter to select the stimuli that were likely to support their hypothesis (Westbury Reference Westbury2005). All voiced obstruents appeared word-initially, because a previous study had shown that the strength of sound-symbolic values of voiced obstruents in Japanese may vary depending on word position (Kawahara et al. Reference Kawahara, Shinohara and Uchimoto2008). No geminates, long vowels or coda nasals appeared anywhere in the stimuli; i.e. all syllables were open. Moreover, because of its potentially salient sound-symbolic values, such as cuteness (Kumagai Reference Kumagai2019), [p] was excluded from the stimuli.
2.2 Procedure
The experiment was distributed as an online experiment using SurveyMonkey.Footnote 5 Within each trial, participants were given one nonce name at a time, and asked to judge whether that name was better for a pre-evolution character or a post-evolution character, i.e. the task was to make a binary decision. The stimuli were presented in the Japanese katakana orthography, which is used to represent real Pokémon names. The participants were asked to base their decision on their intuition, without thinking too much about ‘right’ or ‘wrong’ answers. The order of the stimuli was randomised for each participant.
2.3 Participants
The experiment was advertised on a Pokémon fan website.Footnote 6 A total of 857 participants completed the experiment over a single night. Some previous Pokémonastics experiments had been advertised on the same website (e.g. Kawahara, Godoy & Kumagai Reference Kawahara, Godoy and Kumagai2020), and 124 participants reported that they had either taken part in another Pokémonastics experiment or had studied sound symbolism before. Three participants were non-native speakers of Japanese. The data from these speakers was excluded, and the data from the remaining 730 participants entered into the subsequent analysis.
2.4 Analysis
For statistical analysis, a logistic linear mixed-effects model was fitted, with response (pre-evolution vs. post-evolution) as the dependent variable (Jaeger Reference Jaeger2008). The fixed independent variables included mora count and the presence of a voiced obstruent as well as its interaction. Mora count was centred, because it is a continuous variable (Winter Reference Winter2019). Participants and items were random factors. The model with maximum random structure with both slopes and intercepts (Barr et al. Reference Barr, Levy, Scheepers and Tilly2013) did not converge; hence a simpler model with only random intercepts was interpreted.
3 Results
Figure 4 shows the results. Figure 4a plots ‘post-evolution response ratios’ for each item, averaged over all the participants. The items for the condition with a voiced obstruent are shown with black squares and the items for the condition without a voiced obstruent are shown with grey circles. A logistic curve is superimposed for each voicing condition.

Figure 4 (a) The by-participant averages for each item. The items with a voiced obstruent are shown with black squares and those without a voiced obstruent with grey circles. To avoid overlap, the points are horizontally jittered. Logistic curves are superimposed — the dashed black line represents the condition with a voiced obstruent, and the solid grey line represents the condition without a voiced obstruent. (b) The line plots, with grand averages for each condition.
These results look like the wug-shaped curves illustrated schematically in Fig. 2, consisting of two sigmoid curves separated from each other on the horizontal axis. The relationships between the x-axis and y-axis appear to be closer to sigmoid curves than to a linear function, in that the slope is clearly steepest in the middle range. This is also clear in Fig. 4b, which illustrates the overall pattern by presenting grand averages for each condition – this analysis does not presuppose that sigmoid curves would fit the data points well. The slopes between the 3-mora condition and the 5-mora condition are rather steep. On the other hand, they are not very steep between the 2-mora and 3-mora conditions or between the 5-mora and 6-mora conditions. As Hayes (Reference Hayes2020: 3) puts it, ‘certainty is evidentially expensive’ – we require very strong evidence to be certain that a particular name is that of a pre-evolution or a post-evolution character. A more elaborate defence of using a wug-shaped curve to fit the data is provided in §5.3, once we have developed a full MaxEnt analysis of the data.
A model summary of the linear mixed-effects model appears in Table II. It shows that the two main factors are statistically significant: both longer names and names with voiced obstruents are more likely to be judged better for post-evolution characters. The interaction between the two main factors was not significant.
Table II Summary of the logistic linear mixed-effects model.

4 Discussion
The effect of mora count is an example of counting cumulativity, in that each increase in the mora-count scale contributes to the probability that a name will be judged to be that of a post-evolution character. This effect is evident both with and without a name-initial voiced obstruent. The effect of a voiced obstruent in name-initial position is manifested as a shift between the two sigmoid curves. The two effects together are an example of ganging-up cumulativity – both factors contribute to the judgement of evolvedness. Overall, the results show that counting cumulativity and ganging-up cumulativity can coexist within a single sound-symbolic system. This conclusion is compatible with the results of an artificial language learning experiment on phonotactic learning reported by Breiss (Reference Breiss2020), as well as with the probabilistic phonological alternation patterns discussed by McPherson & Hayes (Reference McPherson and Hayes2016), Zuraw & Hayes (Reference Zuraw and Hayes2017) and Hayes (Reference Hayes2020). See also Breiss (Reference Breiss2020) and Kawahara (Reference Kawahara2020a) for summaries of cumulative effects in phonological alternations and in well-formedness judgement patterns of surface phonotactics.
While the results in Fig. 4 seem to provide a clear case of ‘wug-shaped’ curves, we might wonder if the results could have been different. The answer is positive, as multiple alternative patterns could have arisen from the experimental design. For example, the mora-count effect could have been cumulative, but linear rather than sigmoidal. Indeed, the effect of mora count in the existing Pokémon names actually looks more linear than sigmoidal (see the Appendix for discussion).
Alternatively, the results could have been non-cumulative. For example, there could have been a ‘length threshold’, such that any names shorter than that threshold were judged to be pre-evolution; however, the actual results did not follow such a pattern. Nor did the presence of a voiced obstruent make a name post-evolution in all cases. Instead, both mora counts and voiced obstruents gradiently increased the probabilities of each name being judged to be a post-evolution name.Footnote 7 This point is related to another important aspect of sound symbolism, its stochastic nature (Dingemanse Reference Dingemanse2018, Kawahara et al. Reference Kawahara, Katsuda and Kumagai2019). More generally, Gigerenzer & Gaissmaier (Reference Gigerenzer and Gaissmaier2011) discuss a number of cases in which people making decision adopt ‘a fast and frugal decision heuristics’ approach – they take into account only the most important information, and disregard other information (just as OT with strict domination would do). If people had applied such a fast and frugal heuristics decision-making approach in the current experiment, the results would have been neither stochastic nor cumulative.
Finally, the stochastic nature of sound symbolism provides a parallel to a growing body of evidence that many, but perhaps not all, phonological generalisations have to be stated in a stochastic or probabilistic way; for example, some structures tend to be preferred over others, and some alternations occur with different probabilities in different environments (see §1.1). The current results thus reveal an intriguing parallel between phonological patterns and sound-symbolic patterns.
5 A MaxEnt analysis
The experimental results reported in §3 seem to instantiate a wug-shaped curve, a quantitative signature of the MaxEnt grammar model; the results thus appear to lend support for this grammatical model from the perspective of sound symbolism.Footnote 8 To provide more concrete support for the MaxEnt grammar model, this section develops an analysis of the experimental results using MaxEnt, equipped with the sorts of constraints that have been used in the optimality-theoretic tradition (Prince & Smolensky Reference Prince and Smolensky1993).Footnote 9 A fundamental idea behind this analysis is that sound-symbolic connections – mapping between sounds and meanings – can be understood as involving essentially the same mechanism as phonological input–output mappings (Kawahara et al. Reference Kawahara, Katsuda and Kumagai2019, Kawahara Reference Kawahara2020a). The model deploys the kind of constraints familiar from the OT tradition (Prince & Smolensky Reference Prince and Smolensky1993). To underscore the parallel between phonological analyses and the analysis of sound symbolism developed in this paper, I adopt a particular formalism that has been used to define constraints in the OT research tradition, that of McCarthy (Reference McCarthy2003).
5.1 A brief review of MaxEnt
This section briefly reviews how MaxEnt works in the context of linguistic analyses.Footnote 10 The MaxEnt grammar is similar to OT, in that a set of candidates is evaluated against a set of constraints. Unlike OT, however, constraints are weighted rather than ranked. Consider the toy example in (2). The set of candidates to be evaluated are listed in the leftmost column, and the top row gives the relevant constraints; each constraint is assigned a particular weight (w). The tableau shows the violation profiles of each constraint – how many times each candidate violates a particular constraint.
-
(2)

Based on the constraint-violation profiles, the Harmony score of each candidate x (ℋ-score(x)) is calculated using the formula in (3), where N is the number of relevant constraints, wi is the weight of the ith constraint and Ci(x) is the number of times candidate x violates the ith constraint.
-
(3)

For example, Candidate 2 in tableau (2) violates Constraint B twice and Constraint C once; its ℋ-score is therefore 2 × 2 + 1 × 1 = 5.
The ℋ-scores are negatively exponentiated (eHarmony, represented as e ―H or 1 / eH; according to Hayes Reference Hayes2020, the term was introduced by Colin Wilson in a tutorial presentation at MIT), which is proportional to the probability of each candidate. Intuitively, the more constraint violations a candidate incurs, the higher the ℋ-score, and hence the lower the eHarmony (e ―H). Therefore, more constraint violations lead to that candidate having lower probability. The eHarmony values are relativised against the sum of the eHarmony values of all the candidates, Z, as in (4), where M is the number of candidates.
-
(4)

In the example in (2), Z is 0.0498 + 0.0067 = 0.0565. The predicted probability of each candidate xj, p(xj), is eHarmony(xj) / Z.
5.2 A MaxEnt analysis of the results of the experiment
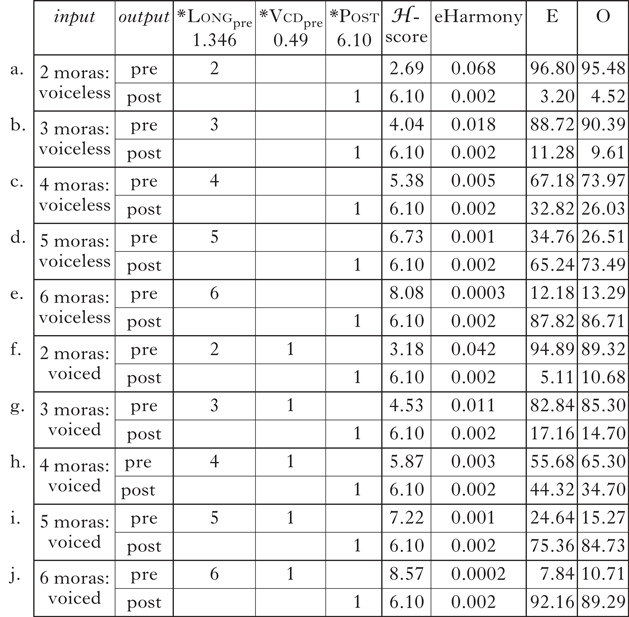
Like most phonological analyses in OT and other related frameworks, a MaxEnt analysis of sound symbolism consists of inputs, outputs and constraints that evaluate the mapping between these two levels of representations. The inputs are phonological forms and the outputs are their sound-symbolic meanings, here either pre-evolution or post-evolution character names. The set of constraints employed in the current analysis is given in (5).Footnote 11 These constraints essentially correspond to OT markedness constraints, in that they evaluate the well-formedness of output structures. The definition of the constraints follows the format in McCarthy (Reference McCarthy2003).
-
(5)

*Longpre-ev prevents long names from being used for pre-evolution characters. This constraint is a formal expression of ‘the longer the stronger’ principle (Kawahara et al. Reference Kawahara, Noto and Kumagai2018) or ‘the iconicity of quantity’ (Haiman Reference Haiman1980, Reference Haiman1984). It is a single gradient/scalar constraint (McPherson & Hayes Reference McPherson and Hayes2016), in that it is a reflection of a single principle, whose violations can be assessed on a numerical scale.Footnote 12 This constraint corresponds to the scalar constraint S used to illustrate the wug-shaped curves in §1.1. *Vcdpre-ev is a formal expression of the preference that character names with voiced obstruents should be used for post-evolution names; this corresponds to the perturber constraint P in §1.1. *Post is a *Struc constraint (Prince & Smolensky Reference Prince and Smolensky1993), which penalises post-evolution character names in general, and corresponds to the binary constraint B discussed in §1.1. We need this constraint because there has to be some constraint that favours pre-evolution character names. All three constraints are statistically motivated by a log-likelihood ratio test, to be presented below in Table III.
Table III The results of the log-likelihood ratio tests. The loglikelihood of the best-fitting model with the three constraints was −432.30. See Supplementary Materials A.

Hayes (Reference Hayes2020) recommends that we conceive of constraint violations as providing evidence for which candidate should be chosen. The constraints posited in (5) do precisely this: the first two constraints offer sound-symbolic evidence to decide on post-evolution names when the candidates are long (*Longpre-ev) or when they contain a voiced obstruent (*Vcdpre-ev), and *Post helps us to decide on a pre-evolution name in general. The weights associated with each constraint reflect the strengths, or cogency, of each piece of evidence.
-
(6)

MaxEnt tableaux for all types of inputs are shown in (6). The leftmost column shows each phonological form, and the second column shows how each phonological form is mapped onto two meanings: pre-evolution character names vs. post-evolution character names. The observed percentages of each condition, shown in the rightmost column, were taken from the grand averages obtained in the experiment. Based on the constraint profiles and the observed percentages of each output form, the optimal weights of these constraints were calculated using the Solver function of Excel (see Supplementary Materials A). The weights obtained by this analysis are shown in the top row of the tableaux. These weights, together with the constraint profiles, allow us to calculate ℋ-scores, eHarmony scores and predicted percentages, using the procedure reviewed in §5.1.
The observed and predicted values are very similar. Figure 5 plots the correlation between the probabilities obtained in the experiment and the probabilities predicted by the MaxEnt model. The figure shows a good fit between the two measures, demonstrating the success of the MaxEnt analysis.

Figure 5 The correlation between the observed and the predicted percentages obtained from the MaxEnt analysis in (6).
One general advantage of MaxEnt is that it allows us to assess the necessity of each constraint using a well-established statistical method, i.e. a log-likelihood ratio test (see e.g. Wasserman Reference Wasserman2004 and Winter Reference Winter2020; also Hayes et al. Reference Hayes, Wilson and Shisko2012 and Breiss & Hayes Reference Breiss and Hayes2020 for applications of this test in linguistic analyses). We can do this by comparing two grammatical models – for the current analysis, we compare the full model incorporating all three constraints with smaller models incorporating two of the three constraints. By removing one of the three constraints, we obtain three simpler two-constraint models. We then compare their log-likelihood values by examining their ratios, which tell us whether the full model fits the data better than the simpler models to a statistically significant degree.
The results of these log-likelihood ratio tests are shown in Table III, which demonstrates that there is statistical justification for all three constraints playing a role in the explanation of the data (see Breiss & Hayes Reference Breiss and Hayes2020: Appendix).
Next, a more complex model was tested, with a fourth constraint representing the interaction term between *Longpre-ev and *Vcdpre-ev, equivalent to the locally conjoined version of these two constraints (cf. Shih Reference Shih2017). The results show that addition of this constraint did not improve the model fit. The Solver actually assigned zero weight to the conjoined constraint. Even when constraint weights were allowed to be negative, the Solver assigned a weight that is very close to zero (―0.13). This is a welcome result, since the interaction of the effects of voiced obstruents and those of mora count followed directly from the architecture of the MaxEnt model itself, obviating the need to posit a specific constraint to capture the interaction between the two factors (see Zuraw & Hayes Reference Zuraw and Hayes2017).
5.3 MaxEnt and wug-shaped curves revisited
Having fully developed the MaxEnt analysis, we can now address a general question regarding wug-shaped curves: whether it is possible to objectively assess if given data is best fitted with a wug-shaped curve. To reiterate, a wug-shaped curve generated by MaxEnt is a mathematical object consisting of two identical sigmoid curves separated on the x-axis. It thus has three essential features: (i) it consists of two sigmoid curves, (ii) the two curves are identical and (iii) they are separate. No real data would perfectly fit this mathematical definition, because it involves some natural variability. Therefore, the question boils down to the issue of how well wug-shaped curves fit the observed data.
Testing whether the two curves are separated on the x-axis is relatively straightforward: it can be assessed by examining the effect of the perturber. In the current analysis, the perturber corresponds to the constraint *Vcdpre-ev, which was significant in the MaxEnt analysis developed in §5.2. Whether the two curves are identical can be addressed by examining the interaction term, because the interaction term represents whether – and how much – the slope should be adjusted from one curve to the other (Winter Reference Winter2019: 138). If the interaction term between *Longpre-ev and *Vcdpre-ev were significant, we could reasonably have concluded that the two curves were not identical to each other. Since the inclusion of the interaction term did not improve the fit of the model, we cannot reject the null hypothesis that the two curves are identical.
In reality, however, it is improbable that we can obtain two curves that are literally identical, because the data in the real world is subject to natural variability. To what extent we allow the two sigmoid curves to be different is a matter that should be examined by empirical investigation, rather than being determined a priori. Two similar, but not identical, sigmoid curves would result in a slightly ‘distorted’ wug-shaped curve. This issue, however, is not just about two lines on a graph; it must instead be understood as a question of whether we should allow interaction terms – or conjoined constraints – to play a substantial role in a MaxEnt grammar. McPherson & Hayes (Reference McPherson and Hayes2016) and Zuraw & Hayes (Reference Zuraw and Hayes2017) posit no interaction terms for their analyses; Shih (Reference Shih2017), on the other hand, argues that constraint conjunction is required even in a MaxEnt grammar. More quantitative studies are necessary to settle this issue.
A final challenge is how to decide whether the pattern is best modelled using a sigmoid curve, which concerns the general issue of which mathematical function to use to fit the data. One useful heuristic is to make use of log-likelihood, the log probability of the observed data being generated by the model (see Zuraw & Hayes Reference Zuraw and Hayes2017, who use this measure to compare different linguistic models). For example, fitting linear functions to the current data yields p(evolved) = ―0.51 + 0.228 × Mora + 0.067 × Voiced obstruent. The log-likelihood of this linear model is ―501.0,Footnote 13 which is worse than the sigmoidal MaxEnt model, which has a log-likelihood of ―432.3. Log-likelihood represents summed log probabilities, so they are always negative. The higher the log-likelihood (i.e. the closer it is to 0), the more likely that the data is generated by the model (i.e. the data is better fitted by the model).
However, relying on log-likelihood alone does not allow us to conclude that the sigmoid function is the function that underlies the actual data. In principle, we can posit a mathematical function with high complexity to achieve the perfect fit to the data; in fact, a function that fits the data perfectly would intersect every data point. However, such functions would be non-restrictive, non-predictive and non-generalisable; i.e. they would suffer from the general problem of overfitting (Good & Hardin Reference Good and Hardin2006). In order to balance the goodness of the fit to the data and model complexity, additional statistical measures, such as the Akaike Information Criterion (AIC; Akaike Reference Akaike, Petov and Caski1973), which take into account the number of free parameters, may prove to be useful (see Shih Reference Shih2017, as well as §6).
Comparing the different sorts of mathematical functions, of which there are many, is beyond the scope of the present paper; in general, however, the choice of mathematical functions to fit linguistic data should be guided by cross-linguistic quantitative observations. For now, I am reasonably confident that mathematical functions generated by MaxEnt are suited to model cross-linguistic quantitative patterns, as reviewed in §1.1.
To conclude this discussion, the current MaxEnt analysis makes specific predictions for forms that contain two voiced obstruents. One of the experiments reported by Kawahara & Kumagai (to appear) shows that nonce names with two voiced obstruents are more likely to be judged as post-evolution character names than nonce names with one voiced obstruent. This result suggests that the effects of voiced obstruents are cumulative, just like the effects of mora count. The definition of *Vcdpre-ev in (5) actually predicts this cumulative behaviour, since forms with two voiced obstruents are assigned two violation marks when they are mapped onto a pre-evolution character. Since the weights of the constraints are already calculated and the constraint-violation profiles are known, the MaxEnt model makes specific quantitative predictions.Footnote 14 These predictions are illustrated in Fig. 6, an example of a ‘stripey wug’ consisting of three sigmoid curves (McPherson & Hayes Reference McPherson and Hayes2016, Zimmermann Reference Zimmermann2017, Zuraw & Hayes Reference Zuraw and Hayes2017, Hayes Reference Hayes2020). While the current experiment was limited to items containing only one voiced obstruent, these predicted values can be tested in future experiments.

Figure 6 Predictions of the current MaxEnt model for forms with two voiced obstruents, instantiating a ‘stripey wug’. See Supplementary Materials B.
This analysis serves to illustrate one strength of explicit constraint formulation in a MaxEnt grammar: it makes specific quantitative predictions about forms that have not yet been seen. As discussed above, choosing a relatively simple model avoids overfitting, and is more likely to generate good predictions for new data.
5.4 Some notes on MaxEnt and logistic regression
I note at this point that MaxEnt is mathematically equivalent to a (multinomial) logistic regression (see in particular Jurafsky & Martin Reference Jurafsky and Martin2019: ch. 5, as well as Shih Reference Shih2017 and Breiss & Hayes Reference Breiss and Hayes2020). A mixed-effects logistic regression analysis was reported in §3 as a means to test the experimental results without any particular linguistic theories or analyses in mind. On the other hand, in this section a MaxEnt analysis has been developed as an explicit, formal analysis within generative grammar to model the knowledge that may underlie the patterns that were identified in the experiment. In order to emphasise that this MaxEnt analysis is indeed a generative phonological analysis, I employed McCarthy's (Reference McCarthy2003) OT constraint schema.
The fact that logistic regression, a general statistical tool, is so well suited to model linguistic patterns is an interesting and thought-provoking observation. As the associate editor notes, one way to understand this convergence is that since MaxEnt (or logistic regression) demonstrably offers a useful tool to discern causes and meanings in data in general, it would not be too surprising if children use logistic regression (or something akin to it) in order to find patterns in the grammar that they are learning. On this view, UG employs some form of logistic regression to learn patterns in the ambient data (see in particular Hayes & Wilson Reference Hayes and Wilson2008, as well as Smolensky Reference Smolensky, Rumelhart and McClelland1986).
Another way to understand MaxEnt within the current phonological research is to consider it as a stochastic extension of OT (Prince & Smolensky Reference Prince and Smolensky1993; see also Breiss & Hayes Reference Breiss and Hayes2020), which invites the interesting question of whether UG can be reduced to a domain-general statistical tool. Providing a full answer to this question is beyond the scope of this paper. However, even if the mapping between two linguistic representations is mediated by a general statistical device, there can be other aspects of UG that remain domain-specific; these include, but are most likely not limited to, (i) the content of the constraints (i.e. Con), (ii) the nature of the vocabulary that this constraint set refers to (e.g. distinctive features such as [+sonorant] and [+voiced], as well as the levels in prosodic hierarchy such as moras and syllables), (iii) how constraint violations can and cannot be assessed (e.g. whether constraints can reward a candidate) and (iv) whether constraints can be conjoined, and if so, to what extent (Potts & Pullum Reference Potts and Pullum2002, McCarthy Reference McCarthy2003, de Lacy Reference de Lacy2006, Crowhurst Reference Crowhurst2011, Coetzee & Kawahara Reference Coetzee and Kawahara2013, among many others). Restricting Con may be necessary to explain cases in which speakers’ behaviour diverges substantially from what is predicted by the statistical patterns in the lexicon (e.g. Becker et al. Reference Becker, Ketrez and Nevins2011, Jarosz Reference Jarosz2017, Garcia Reference Garcia2019). Additionally, UG may impose particular biases toward, for example, phonetically natural patterns, which can be formalised in the MaxEnt framework in terms of biases on constraint weights (Wilson Reference Wilson2006, Hayes et al. Reference Hayes, Zuraw, Siptár and Londe2009, Hayes & White Reference Hayes and White2013). In short, UG can be a metatheory of constraints. Since MaxEnt allows us to statistically access the necessity of each constraint by way of log-likelihood tests, it may prove to be a useful tool to explore in a quantitatively rigorous manner what Con consists of (Shih Reference Shih2017).
6 Analyses with Stochastic Optimality Theory
Although Zuraw & Hayes (Reference Zuraw and Hayes2017) and Hayes (Reference Hayes2020) argue that patterns with wug-shaped curves cannot be modelled well with Stochastic OT (Boersma Reference Boersma1998, Boersma & Hayes Reference Boersma and Hayes2001), this section reports several attempts to fit a Stochastic OT model to the current data. In Stochastic OT, each constraint is assigned a particular ranking value, which is perturbed by Gaussian noise at each evaluation. Just as in Classic OT, each evaluation is computed with strict domination, predicting a single winner in each evaluation trial. The probability distributions of variable outputs are calculated over multiple evaluation cycles.
To analyse the current experimental results using Stochastic OT, the same data structure that was used for the MaxEnt analysis in (6) was fed to OTSoft (Hayes et al. Reference Hayes, Tesar and Zuraw2014), using the Gradual Learning Algorithm (Boersma & Hayes Reference Boersma and Hayes2001). The initial ranking values of all constraints were set at 100 (the default value). The initial plasticity and the final plasticity were set at 0.01 and 0.001 respectively. There were 1,000,000 learning trials, and the grammar was tested for 1,000,000 cycles in order to obtain the predicted probability distribution. The results of all the learning simulations presented in this section are available in Supplementary Materials D.
This learning simulation yielded the following ranking values: *Longpre-ev = 99.6, *Vcdpre-ev = 98.1, *Post = 100.4. All the constraints were active in at least one of the evaluation trials. A problem with this Stochastic OT analysis is that it was not able to model the effects of mora count at all; indeed, Stochastic OT does not handle counting cumulativity effects well in general (Jäger Reference Jäger, Zaenen, Simpson, King, Grimshaw, Maling and Manning2007, Hayes Reference Hayes2020). For all the conditions without voiced obstruents, regardless of the mora counts, post-evolution candidates were predicted to win in 40% of the cases and pre-evolution candidates in 60%. For all the conditions with voiced obstruents, post-evolution characters were predicted to win in 46.6% of the cases and pre-evolution characters in 53.4%. Stochastic OT was thus able to model the effect of voiced obstruents (40% vs. 46.6%), which seems to reflect the actual observed post-evolution response values averaged across all the mora-count conditions (40.1% vs. 46.8%). However, it was unable to learn the mora-count effects.
The failure to model the counting cumulativity effects of mora count is due to the fact that Stochastic OT is no different from Classic OT (Prince & Smolensky Reference Prince and Smolensky1993) at each time of evaluation. OT does not distinguish between, for example, one violation mark vs. two violation marks on the one hand and one violation mark vs. four violation marks on the other. Therefore, if *Post dominates *Longpre-ev at a particular time of evaluation, then the pre-evolution candidate is predicted to win at that particular time of evaluation, no matter how many violations of *Longpre-ev the pre-evolution candidate incurs. Similarly, if *Longpre-ev dominates *Post, the post-evolution candidate wins, no matter how long the pre-evolution candidate is. The number of violations is irrelevant in Classic OT or Stochastic OT, because of strict domination. For these reasons, it was not able to account for the counting cumulativity effects of mora counts.
A (partial) solution to this problem involves splitting up *Longpre-ev into a set of separate constraints which each penalise a pre-evolution name with a particular mora count; i.e. *Long(3μ)pre-ev, *Long(4μ)pre-ev, *Long(5μ)pre-ev and *Long(6μ)pre-ev (see McPherson & Hayes Reference McPherson and Hayes2016: n. 21, as well as Boersma Reference Boersma1998, Gouskova Reference Gouskova2004 and de Lacy Reference de Lacy2006). A new learning simulation was run with the same parameter settings. With the expanded set of constraints, it learned the following values: *Long(3μ)pre-ev = 97.2, *Long(4μ)pre-ev = 99.7, *Long(5μ)pre-ev = 103.7, *Long(6μ)pre-ev = 103.2, *Vcdpre-ev = 98.7, *Post = 101.6. Plotting the predicted probabilities based on these ranking values results in two separate curves for the two voicing conditions, as shown in Fig. 7. However, these curves formed an ‘open jaw’ pattern, in which we observe the convergence of the two curves at one end and divergence at the other end, with the difference between the two curves increasing monotonically toward the left (compare this pattern with Fig. 4b).

Figure 7 The probability patterns predicted by the GLA when *Longpre-ev is split into a family of different constraints.
The problem comes from the fact that the ranking value of the perturber constraint – *Vcdpre-ev – differs too much from the ranking values of *Long(5μ)pre-ev, *Long(6μ)pre-ev and *Post, resulting in ‘near strict domination’. As a result, *Vcdpre-ev does not have a visible influence on 5-mora and 6-mora names. This problem is a general one (Hayes Reference Hayes2020): the perturber constraint can have only one ranking value, and hence has a hard time exerting its influence across the whole x-axis range when it is placed near one end of the constraint-value continuum.
This aspect of Stochastic OT was identified by Zuraw & Hayes (Reference Zuraw and Hayes2017) in their quantitative analysis of French liaison. Indeed, the general constraint profiles for the current analysis are similar to those for their analysis of French. The set of *Long(nμ)pre-ev constraints and *Vcdpre-ev are synergistic, in that they both favour post-evolution names, while the other constraint, *Post, favours pre-evolution names. Zuraw & Hayes (Reference Zuraw and Hayes2017: 530) offer an intuitive explanation of how this type of constraint-violation profile results in a pattern like the one in Fig. 7. Citing unpublished work by Giorgio Magri, they characterise this pattern as ‘[two curves] will be uniformly converging in one direction and diverging in the other … where [the] differences … grow monotonically toward the right of the plot’. The pattern in Fig. 7 looks precisely like what Zuraw & Hayes describe, with the very minor difference that the divergence is larger on the left of the plot in Fig. 7, rather than on the right.
Bruce Hayes (personal communication) points out that Stochastic OT may perform better if the perturber constraint (*Vcdpre-ev) is reformulated in such a way that it penalises the same candidate as the binary constraint (*Post). Following this suggestion, I reformulated *Vcdpre-ev as a constraint that penalises a post-evolution name which does not start with a voiced obstruent, as in (7).
-
(7)

This new constraint is reminiscent of a positional markedness constraint, which for example, requires a low-sonority segment in onset positions (Smith Reference Smith2002). Unlike *Vcdpre-ev, it penalises a post-evolution name (rather than a pre-evolution name) when it does not have a particular property. The ranking values that the General Learning Algorithm learned with the constraint in (7) are *Long(3μ)pre-ev = 64.6, *Long(4μ)pre-ev = 65.9, *Long(5μ)pre-ev = 69.9, *Long(6μ)pre-ev = 70.4, InitialC=Vcdpost-ev = 66.6, *Post = 67.5, which yields the two curves shown in Fig. 8.

Figure 8 The probability patterns predicted by the GLA with the perturber constraint in (7).
The two curves are better separated in Fig. 8 than in Fig. 7, because the ranking value of the perturber constraint, InitialC=Vcdpost-ev, is in the middle of the constraint-ranking continuum in this analysis. We can see that the difference between the two curves is largest for 4-mora names, and becomes smaller as the name gets shorter or longer. If we had a larger range of x-axis values, the separation of the two curves should eventually disappear at both ends, predicting a ‘cucumber curve’, in which the difference between the two curves monotonically become larger as we move toward the middle of the horizontal axis.
As demonstrated in this section, Stochastic OT requires that we split the scalar constraint (*Longpre-ev) into a set of multiple constraints (Boersma Reference Boersma1998, McPherson & Hayes Reference McPherson and Hayes2016) to account for the counting cumulativity effect, thus requiring the greater number of free parameters. In addition, the problem identified by Hayes (Reference Hayes2020), also observed in the analyses here, is a general one: the perturber constraint can have only one ranking value, so its influence is localised. When it is placed in the middle of the ranking-value continuum, as in Fig. 8, we observe a global separation of the two curves, as long as the x-axis range is sufficiently limited. If the x-axis has a wider range, however, it is predicted that the perturber cannot influence the whole x-axis range.
The log-likelihood – a measure of deviation between the observed data and the model predictions – of the Stochastic OT analyses was calculated. The values for the two analyses were ―459.6 (Fig. 7) and ―546.8 (Fig. 8).Footnote 15 These values are lower than that of the MaxEnt model (―432.3) (recall that log-likelihood values that are closer to 0 are better). Moreover, the Stochastic OT models and the MaxEnt model differ in terms of the number of free parameters (i.e. the number of constraints): six vs. three. The AIC was therefore calculated for each model, yielding 931.2 and 1105.5 for the two Stochastic OT models and 870.7 for the MaxEnt model (a model with a lower AIC makes a better prediction).Footnote 16
7 Concluding remarks
7.1 Summary
The current project was largely inspired by the research programme proposed by Hayes (Reference Hayes2020). In order to compare various stochastic linguistic models, it is useful to think abstractly about what quantitative predictions the competing theories make. Taking MaxEnt as an example, Hayes (Reference Hayes2020) shows that we should be able to identify wug-shaped curves under certain circumstances. The experiment in this paper addressed this prediction in the domain of sound symbolism, and showed that we can indeed identify wug-shaped curves when certain variables are systematically manipulated for the judgement of evolvedness in Pokémon names. To the extent that wug-shaped curves are typical quantitative signatures of MaxEnt, this shows that MaxEnt is a grammatical framework that is suitable for modelling sound-symbolic patterns in natural languages (Kawahara et al. Reference Kawahara, Katsuda and Kumagai2019, Kawahara Reference Kawahara2020a). To put the results in a more theory-neutral fashion, Japanese speakers take into account different sources of information (mora counts and voiced obstruents) in a cumulative way, more specifically, in a way that is naturally predicted by MaxEnt.
Viewed from a slightly different – albeit related – perspective, the experiment addressed the general issue of cumulativity in sound symbolism. The effects of mora counts were an example of counting cumulativity, in that each mora count contributed to the judgement of evolvedness in a sigmoidal fashion. The overall patterns also instantiated ganging-up cumulativity, in that the effects of voiced obstruents and of mora counts additively contributed to the judgement of evolvedness. Such cumulative patterns are a natural consequence of MaxEnt.
7.2 Phonological patterns and sound-symbolic patterns
To the extent that MaxEnt is a useful tool for modelling phonological patterns such as input–output mappings and surface phonotactics judgements, as many previous studies have already shown (e.g. Hayes & Wilson Reference Hayes and Wilson2008, McPherson & Hayes Reference McPherson and Hayes2016, Zuraw & Hayes Reference Zuraw and Hayes2017), the overall results point to an intriguing parallel between phonological patterns and sound-symbolic patterns. Traditionally, sound symbolism received hardly any serious attention from formal phonologists (but see Alderete & Kochetov Reference Alderete and Kochetov2017, Kawahara Reference Kawahara2020b). However, the results suggest that there may be non-negligible similarities between sound–meaning mappings and phonological input–output mappings (as well as well-formedness judgements of surface phonotactic patterns). Phonological patterns and sound-symbolic patterns share two important properties, stochasticity and cumulativity, both of which follow naturally from a MaxEnt grammar. This conclusion in turn implies that sound symbolism may not be as irrelevant to formal phonological theory as has been assumed in the past, echoing the claim recently made by several researchers (Alderete & Kochetov Reference Alderete and Kochetov2017, Kumagai Reference Kumagai2019, Jang Reference Jang2020, Kawahara Reference Kawahara2020b, Shih Reference Shih2020).Footnote 17
If this hypothesis is on the right track, one question that arises is how closely these two systems are related to one another. I am unable to offer a full answer to this general question here, but can address it partially by asking a more concrete question: whether sound-symbolic constraints of the sort used in this paper can trigger phonological changes. Alderete & Kochetov (Reference Alderete and Kochetov2017) argue that such patterns do exist. Patterns of expressive palatalisation, often found in baby-talk registers, exhibit properties that are different from ‘regular’ phonological palatalisation processes; for example, the former can target all the coronal segments in a word without a clear trigger like a high front vowel (e.g. Japanese /osakana-saɴ/ → [oɕakaɲa-ɕaɴ] ‘fish-y’). They thus argue that expressive palatalisation patterns are caused by sound-symbolic requirements, instead of constraints that are purely phonological, and propose a family of Express(X) constraints, which demands that a particular meaning is expressed by a particular sound. Expressive palatalisation may thus instantiate a case in which sound-symbolic constraints coerce phonological changes. See Kumagai (Reference Kumagai2019) and Jang (Reference Jang2020) for other possible examples.
7.3 Closing remarks
I would like to close this paper by putting forward the following methodological thesis: phonological theory can inform research on sound symbolism. Although there is a great deal of current work on sound symbolism, most of this research has been conducted by psychologists, cognitive scientists and cognitive linguists, and few formal phonologists have paid serious attention to sound symbolism. However, the research reported in this paper has revealed important aspects of sound symbolism – its cumulative nature and how it can be modelled using MaxEnt. Hayes (Reference Hayes2020) offers an abstract ‘top-down’ approach, which takes one theory seriously and considers its consequences. The research discussed here would not have been possible without this approach. More generally, then, phonological theory can inform research on sound symbolism in important ways. In addition, I hope to have shown that sound symbolism can offer a new testing ground for the examination of how the cumulative nature of linguistic patterns is manifested, and of how sound symbolism can inform phonological theories. More generally, the case study in this paper has shown that phonological theories and research on sound symbolism can and should mutually inform each other.
Appendix: Patterns in existing Pokémon names
We might wonder how the existing patterns of Pokémon names behave with respect to the issues discussed in the main text. To address this question, I used the dataset compiled by Kawahara et al. (Reference Kawahara, Noto and Kumagai2018), which includes all the data up to the sixth generation, about 700 characters. Some Pokémon characters do not undergo evolution at all, and those were removed from the analysis. Some others were ‘baby’ Pokémons, introduced as a pre-evolution version of an already existing character in a later series. While there were not many (N = 16), they were also excluded. Pokémons can undergo evolution twice; in the current analysis, as long as they had evolved once, they were counted as post-evolution. There was only one 6-mora name, so this data point has to be interpreted with caution. The total N was 585 in this analysis.
In order to examine whether we observe a sigmoid curve in the analysis of existing Pokémon names, Fig. 9a plots the relationship between the mora counts and the averaged probabilities of the names being used for post-evolution characters. Both a linear function (solid line) and a sigmoid curve (dashed line) were fitted to the data. There does not seem to be any good reason to believe that the sigmoid curve fits the data better than the linear function. The analysis reported by Kawahara et al. (Reference Kawahara, Noto and Kumagai2018), which makes use of a four-way distinction in terms of evolution – baby Pokémon, no-evolution, evolved once and evolved twice (coded as ―1, 0, 1, 2 respectively) – shows a similar linear trend, as shown as Fig. 9b (based on Kawahara et al. Reference Kawahara, Noto and Kumagai2018: Fig. 7).

Figure 9 (a) The relationship between the mora count and the averaged probabilities of post-evolution in the existing names, in which evolution is coded as a binary variable. (b) The correlation between the number of moras and the average evolution levels, in which evolution is coded as a four-way variable.
We may tentatively conclude from Fig. 9 that sigmoid curves (and hence wug-shaped curves) emerged as a result of the experimental settings, despite the absence of such patterns in the existing names.
An anonymous reviewer raises the question of where this difference between the real names and experimental results comes from, asking if MaxEnt would force a linear pattern in the input to be converted to a sigmoidal pattern in the output. The answer is positive. Because of the mathematics that underlies MaxEnt, a scalar constraint has to result in a sigmoid curve, not a linear curve (McPherson & Hayes Reference McPherson and Hayes2016, Zuraw & Hayes Reference Zuraw and Hayes2017, Jurafsky & Martin Reference Jurafsky and Martin2019, Winter Reference Winter2019).
A question that arises is why we observe a linear pattern in the existing names, rather than a sigmoid curve. My tentative hypothesis is that, since the experiment focused on sound symbolism using nonce names, it was able to tap into how sound-symbolic knowledge is revealed in a more pure and direct form than would be the case if we had looked at the set of existing names. Sound symbolism is not the only factor that determines existing Pokémon names; other factors are also taken into consideration, such as the occasional use of real words to describe a character; e.g. hitokage ‘fire lizard’ is a kind of a lizard (tokage) which spits out fire (hi). Another complication is that the Pokémon lexicon has evolved over a number of generations, with new characters added in each generation. The question of why the existing names show a linear pattern requires further scrutiny, but the experimental results reported here nevertheless remain encouraging, because, as we have seen, MaxEnt can have a linear input, but has to return a sigmoidal output, as confirmed by the current experiment.