Hostname: page-component-5c6d5d7d68-pkt8n Total loading time: 0 Render date: 2024-08-19T23:19:01.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Improving Poisson Approximations

Published online by Cambridge University Press:  27 July 2009

Erol A. Peköz  and
Sheldon M. Ross
Erol A. Peköz
Affiliation:
Department of Industrial Engineering and Operations Research, University of California, Berkeley Berkeley, California 94720
Sheldon M. Ross
Affiliation:
Department of Industrial Engineering and Operations Research, University of California, Berkeley Berkeley, California 94720
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X1,…, Xn, be indicator random variables, and set 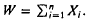We present a method for estimating the distribution of W in settings where W has an approximately Poisson distribution. Our method is shown to yield estimates significantly better than straight Poisson estimates when applied to Bernoulli convolutions, urn models, the circular k of n: F system, and a matching problem. Error bounds are given.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 8 , Issue 4 , October 1994 , pp. 449 - 462
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Aldous, D. (1989). The harmonic mean formula for probabilities of unions: Applications to sparse random graphs. Discrete Mathematics 76: 167–176.CrossRefGoogle Scholar
2.Barbour, A.D., Hoist, L., & Janson, S. (1992). Poisson approximation. Oxford: Oxford University Press.CrossRefGoogle Scholar
3.Peköz, E. & Ross, S.M. (1994). A simple derivation of exact reliability formulas for linear and circular consecutive k-of-n:F systems. Journal of Applied Probability (to appear).Google Scholar
4.Ross, S.M. (1994). Estimating a convolution tail probability by simulation. Probability, Statistics, and Optimization: A Tribute to Peter Whittle. New York: Wiley.Google Scholar
5.Ross, S.M. (to appear). A new simulation estimator of system reliability. Journal of Applied Mathematics and Stochastic Analysis.Google Scholar
6.Stein, C. (1986). Approximate computation of expectations. IMS Lecture Notes, Hayward, CA.CrossRefGoogle Scholar