Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Peköz, Erol A.
and
Ross, Sheldon M.
1995.
A simple derivation of exact reliability formulas for linear and circular consecutive-k-of-n: F systems.
Journal of Applied Probability,
Vol. 32,
Issue. 02,
p.
554.
Peköz, Erol A.
and
Ross, Sheldon M.
1995.
A simple derivation of exact reliability formulas for linear and circular consecutive-k-of-n: F systems.
Journal of Applied Probability,
Vol. 32,
Issue. 2,
p.
554.
Peköz, Erol A.
1996.
Stein's method for geometric approximation.
Journal of Applied Probability,
Vol. 33,
Issue. 3,
p.
707.
Peköz, Erol A.
1996.
Stein's method for geometric approximation.
Journal of Applied Probability,
Vol. 33,
Issue. 3,
p.
707.
Yue, Peng
Forrest, William F.
Kaminker, Joshua S.
Lohr, Scott
Zhang, Zemin
and
Cavet, Guy
2010.
Inferring the functional effects of mutation through clusters of mutations in homologous proteins.
Human Mutation,
Vol. 31,
Issue. 3,
p.
264.


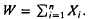 We present a method for estimating the distribution of
We present a method for estimating the distribution of 