Hostname: page-component-77c89778f8-vpsfw Total loading time: 0 Render date: 2024-07-19T10:29:25.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Product-Type Probability Bounds of Higher Order

Published online by Cambridge University Press:  27 July 2009

Hentry W. Block ,
Tim Costigan  and
Allan R. Sampson
Hentry W. Block
Affiliation:
Department of Mathematics and StaatisticsUniversity of Pittsburgh Pittsburgh, Pennsylvania 15260
Tim Costigan
Affiliation:
Department of StatisticsThe Ohio State University, 141 Cockins Hall 1958 Neil Avenue Columbus, Ohio 43210-1247
Allan R. Sampson
Affiliation:
Department of Mathematics and StatisticsUniversity of Pittsburgh Pittsburgh, Pennsylvania 15260
Get access Rights & Permissions [Opens in a new window]

Abstract

GIaz and Johnson [14] introduce ith-order product-type approximations, βi, i =1,…n − 1, for Pn = P(X1 ≤c1, X2 ≤ c2,…Xn≤ cn) and show that Pn≥ βn−1 ≥ βn−2 ≥… ≥ β2 ≥ β1 when X is MTP2. In this article, it is shown that

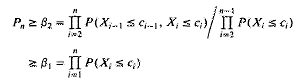
under weaker positive dependence conditions. For multivariate normal distributions, these conditions reduce to cov(Xi,Xj) ≥ 0 for 1 ≤ i < j ≤ n and cov(Xi,Xj| Xj−1) ≥ 0 for 1 ≤ i < j − 1, j = 3,…,n. This is applied to group sequential analysis with bivariate normal responses. Conditions for Pn ≥ β3 ≥ β2 ≥β1 are also derived. Bound conditions are also obtained that ensure that product-type approximations are nested lower bounds to upper orthant probabilities P(X1 > C1,…,Xn > cn). It is shown that these conditions are satisfied for the multivariate exponential distribution of Marshall and Olkin [20].

Type
Articles
Information
Probability in the Engineering and Informational Sciences , Volume 6 , Issue 3 , July 1992 , pp. 349 - 370
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, T.W. (1984). An introduction to multivariate statistical analysis. New York: Wiley.Google Scholar
Barlow, R.E. & Proschan, F. (1981). Statistical theory of reliability and life testing probability models. Silver Springs, MD: To Begin With.Google Scholar
Bauer, P. (1986). Two stage testing for simultaneously testing main and side effects in clinical trials. Biometrical Journal 28: 871–879.CrossRefGoogle Scholar
Bauer, P. & Hackl, P. (1985). The application of Hunter's inequality in simultaneous testing. Biometrical Journal 27: 25–38.CrossRefGoogle Scholar
Block, H.W. & Sampson, A.R. (1988). Conditionally ordered distributions. Journal of Multivan ate Analysis 27: 91–104.CrossRefGoogle Scholar
Block, H.W. & Ting, M.L. (1981). Some concepts of multivariate dependence. Communtcations in Statistics, Series A 10: 749–762.Google Scholar
Bolviken, E. (1982). Probability inequalities for the multivariate normal with non-negative partial correlations. Scandinavian Journal of Statistics 9: 49–58.Google Scholar
Chhetry, D. (1983). Some concepts of setwise positive dependence. Ph.D. dissertation, University of Texas at Dallas.Google Scholar
Chhetry, D., Kimeldorf, G., & Sampson, A.R. (1989). Concepts of setwise dependence. Probability in the Engineering and Informational Sciences 3: 367–380.CrossRefGoogle Scholar
Cornish, E.A. (1954). The multivariate t-distribution associated with a set of normal deviates. Australian Journal of Physics 7: 531–542.CrossRefGoogle Scholar
Coostigan, T.M. (1988). Product-type probability bounds. Ph.D. dissertation, University of Pittsburgh.Google Scholar
Dunnett, C.W. & Sobel, M. (1954). A bivariate generalization of student's t-distribution, with tables for certain special cases. Biometrika 41: 153–169.CrossRefGoogle Scholar
Esary, J.D., Proschan, F., & Walkup, D. (1967). Association of random variables with applications. Annals of Mathematical Statistics 38: 1466–1474.CrossRefGoogle Scholar
Glaz, J. & Johnson, Mck, B.. (1984). Probability inequalities for multivariate distributions with dependence structures. Journal of the American Statistical Association 79: 436–441.CrossRefGoogle Scholar
Glaz, J. & Johnson, B. McK. (1986). Approximating boundary crossing probabilities with application.to sequential tests. SequenlialAnalysis 5 (No. 1): 37–72.Google Scholar
Karlin, S. & Rinott, Y. (1980). Classes of orderings of measures and related correlation inequalities- 1: Multivariate totally positive distributions. Journal of Multivariate Analysis 10: 476–498.Google Scholar
Karlin, S. & Rinott, Y. (1983). M-matrices as covariance matrices of multinormal distributions. Linear Algebra and Its Applications 52/53: 419–438.CrossRefGoogle Scholar
Kenyon, J.R. (1987). Bounds and approximations for multivariate probabilities: Their calculation and applications. Ph.D. dissertation, University of Connecticut, Storrs.Google Scholar
Lee, M. L. Ting (1985). Dependence by total positivity. Annals of Probability 13: 572–582.CrossRefGoogle Scholar
Marshall, A. & Olkin, I. (1967). A multivariate exponential distribution. Journal of the American Statistical Association 62: 30–44.CrossRefGoogle Scholar
Milhako, D. (1987). Repeated significance testing in survival analysis using litter-matched design. Biometrics 43: 115–125.CrossRefGoogle Scholar
Nauss, J. I. (1982). Approximations for distributions of scan statistics. Journal of the American Statistical Association 77: 177–183.CrossRefGoogle Scholar
Sampson, A.R. (1983). Positive dependence properties of elliptically symmetric distributions. Journal of Multivariate Analysis 13: 375–381.CrossRefGoogle Scholar
Sarkar, S.K. & Smith, W. (1986). Probability inequalities for ordered MTP2 random variables. Sankya 48 (Ser. A. Pt. 2): 119–135.Google Scholar
Sidak, Z. (1967). Rectangular confidence regions for means of multivariate normal distributions. Journal of the American Statistical Association 62: 626–633.Google Scholar
Slepian, D. (1962). On one-sided barrier problem for Gaussian noise. Bell System Technical Journal 41: 463–501.CrossRefGoogle Scholar
Thall, P.F., Simon, R., & Ellenberg, S.S. (1988). Designs for comparative clinical trials. Biometrika 75: 303–310.CrossRefGoogle Scholar
Tong, Y.L. (1980). Probability inequalities in multivariate distributions. New York: Academic Press.Google Scholar