Hostname: page-component-5c6d5d7d68-qks25 Total loading time: 0 Render date: 2024-08-31T23:01:20.817Z Has data issue: false hasContentIssue false
  • English
  • Français

A SPECTRUM OF SERIES–PARALLEL GRAPHS WITH MULTIPLE EDGE EVOLUTION

Part of: Limit theorems Operations research and management science Combinatorial probability Graph theory

Published online by Cambridge University Press:  26 January 2019

Hosam M. Mahmoud
Hosam M. Mahmoud*
Affiliation:
Department of Statistics, The George Washington University, Washington, D.C., 20052, USA E-mail: hosam@gwu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We discuss a rich family of directed series–parallel (SP) graphs grown by the simultaneous random series or parallel development of multiple edges. The family portrays a spectrum that spans a wide range of SP graphs: from simple models, where only as few as one edge is chosen for evolution at each discrete point in time, to complex hierarchical lattice networks grown by a take-all strategy, where all the edges in the existing network are developed.

The family of SP graphs we discuss is grown from an initial seed graph with τ0 edges under an arbitrary building sequence, 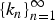$\{k_{n}\}_{n=1}^{\infty}$, of nonnegative integers (with 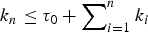$k_n \le \tau _0 + \sum\nolimits_{i = 1}^n {k_i} $, for arbitrary τ0 ≥ 1), that specifies the number of edges subjected to evolution at time n. We study the average north polar degree and show that we can go beyond averages to strong laws. We also find the exact average number of critical edges. The asymptotics of the critical edges are facilitated under the regularity condition that 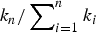$k_n/\sum\nolimits_{i = 1}^n {k_i} $ converges to a constant (as n → ∞), a natural condition easily met by practical strategies, such as single-edge evolution and take-all choice, and much in between.

Keywords

flow in graphmartingalenetworkrandom graphrecurrence

MSC classification

Primary: 60C05: Combinatorial probability 05C80: Random graphs 90B15: Network models, stochastic
Secondary: 60F15: Strong theorems 05C21: Flows in graphs
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 33 , Issue 4 , October 2019 , pp. 487 - 499
Copyright
Copyright © Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barabási, A. (2016). Network science. Cambridge, UK: Cambridge University Press.Google Scholar
2.Bernasconi, N., Panagiotou, K., & Steger, A. (2008). On the degree sequences of random outerplanar and series-parallel graphs. Lecture Notes in Computer Science 5171: 303–316.Google Scholar
3.Drmota, M. (2008). Random trees: an interplay between combinatorics and probability. Springer.Google Scholar
4.Drmota, M., Giménez, O., & Noy, M. (2010). Vertices of given degree in series-parallel graphs. Random Structures & Algorithms 36: 273–314.Google Scholar
5.Feng, Y., Mahmoud, H., & Rüschendorf, L. (2016). Degree profile of hierarchical lattice networks. Probability in the Engineering and Informational Sciences 31: 60–82.Google Scholar
6.Hall, P. & Heyde, C. (1980). Martingale limit theory and its application. New York: Academic Press Inc.Google Scholar
7.Hambly, B. & Jordan, J. (2004). A random hierarchical lattice: the series-parallel graph and its properties. Advances in Applied Probability 36: 824–838.Google Scholar
8.Hibbard, T. (1962). Some combinatorial properties of certain trees with applications to searching and sorting. Journal of the ACM 9: 13–28.Google Scholar
9.Hofri, M. & Mahmoud, H. (2016). Algorithmics of nonuniformity: tools and paradigms. Boca Raton, FL: Chapman-Hall.Google Scholar
10.Hofri, M., Li, C., & Mahmoud, H. (2016). On the combinatorics of binary series-parallel graphs. Probability in the Engineering and Informational Sciences 30: 224–260.Google Scholar
11.Kendall, M., Stuart, A., & Ord, K. (1987). Advanced theory of statistics. Vol. I. Distribution Theory. Oxford University Press.Google Scholar
12.Knuth, D. (1973). The art of computer programming. Vol. 3. Reading, MA: Addison-Wesley.Google Scholar
13.Mahmoud, H. (1992). Evolution of random search trees. New York: John Wiley & Sons.Google Scholar
14.Mahmoud, H. (2013). Some node degree properties of series-parallel graphs evolving under a stochastic growth model. Probability in the Engineering and Informational Sciences 27: 297–307.Google Scholar
15.Mahmoud, H. (2014). Some properties of binary series-parallel graphs. Probability in the Engineering and Informational Sciences 28: 565–572.Google Scholar
16.Ross, S. (1996). Stochastic processes. New York: Wiley.Google Scholar
17.Szpankowski, W. (2011). Average case analysis of algorithms on sequences. New York: Wiley.Google Scholar
18.Van der Hofstad, R. (2017). Random graphs and complex networks. Vol. 1. Cambridge, UK: Cambridge University Press.Google Scholar