No CrossRef data available.
Article contents
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
Part of:
Harmonic analysis in several variables
Exponential sums and character sums
Additive number theory; partitions
Published online by Cambridge University Press: 15 March 2024
Abstract
We consider spectral projectors associated to the Euclidean Laplacian on the two-dimensional torus, in the case where the spectral window is narrow. Bounds for their L2 to Lp operator norm are derived, extending the classical result of Sogge; a new question on the convolution kernel of the projector is introduced. The methods employed include 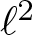 $\ell^2$ decoupling, small cap decoupling and estimates of exponential sums.
$\ell^2$ decoupling, small cap decoupling and estimates of exponential sums.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
Blair, M. D., Huang, X. and Sogge, C. D., Improved spectral projection estimates, (2022), preprint, arXiv:2211.17266.Google Scholar
Bombieri, E. and Bourgain, J., A problem on sums of two squares, Int. Math. Res. Not. 2015(11) (2015), 3343–3407.Google Scholar
Bombieri, E. and Pila, J., The number of integral points on arcs and ovals, Duke Math. J. 58(1) (1989), 337–357.Google Scholar
Bourgain, J., Eigenfunction bounds for the Laplacian on the n-torus, Int. Math. Res. Not. 1993(3) (1993), 61–66.CrossRefGoogle Scholar
Bourgain, J., Moment inequalities for trigonometric polynomials with spectrum in curved hypersurfaces, Isr. J. Math. 193(1) (2013), 441–458.CrossRefGoogle Scholar
Bourgain, J., Burq, N. and Zworski, M., Control for Schrödinger operators on 2-tori: rough potentials, J. Eur. Math. Soc. 15(5) (2013), 1597–1628.CrossRefGoogle Scholar
Bourgain, J. and Demeter, C., Improved estimates for the discrete Fourier restriction to the higher dimensional sphere, Isr. J. Math. 57(1) (2013), 213–227.Google Scholar
Bourgain, J. and Demeter, C., New bounds for the discrete Fourier restriction to the sphere in 4D and 5D, Int. Math. Res. Not. IMRN 2015(11) (2015), 3150–3184.Google Scholar
Bourgain, J. and Demeter, C., The proof of the l 2 decoupling conjecture, Ann. Math. 182 (2015), 351–389.CrossRefGoogle Scholar
Bourgain, J., Shao, P., Sogge, C. and Yao, X., On lp-resolvent estimates and the density of eigenvalues for compact Riemannian manifolds, Commun. Math. Phys. 333(3) (2015), 1483–1527.CrossRefGoogle Scholar
Cooke, R., A Cantor–Lebesgue theorem in two dimensions, Proc. Am. Math. Soc. 30(3) (1971), 547–550.CrossRefGoogle Scholar
Demeter, C., Guth, L. and Wang, H., Small cap decouplings, Geom. Funct. Anal. 30(4) (2020), 989–1062. With an appendix by D. R. Heath-Brown.CrossRefGoogle Scholar
Fu, Y., Guth, L. and Maldague, D., Sharp superlevel set estimates for small cap decouplings for the parabola. https://arxiv.org/pdf/2107.13139.pdf.Google Scholar
Germain, P. and Myerson, S., Bounds for spectral projectors on the euclidean cylinder, C. R. Math. 360(G11) (2022), 1257–1262.CrossRefGoogle Scholar
Germain, P. and Myerson, S. L. R., Bounds for spectral projectors on tori. In Forum of Mathematics, Sigma, Volume 10, (Cambridge University Press, 2022).Google Scholar
Germain, P. and Rydin Myerson, S. L., Bounds for spectral projectors on generic tori, Math. Ann. 388 (2022), 1–37.Google ScholarPubMed
Guo, J., On lattice points in large convex bodies, Acta Arith. 151 (2012), 83–108.CrossRefGoogle Scholar
Hickman, J., Uniform lp resolvent estimates on the torus, Math. Res. Reports 1 (2020), 31–45.CrossRefGoogle Scholar
Huxley, M. N., Area, Lattice points, and Exponential sums, Volume 13, (Clarendon Press, 1996).CrossRefGoogle Scholar
Huxley, M. N., Exponential sums and lattice points iii, Proc. London Math. Soc. 87(3) (2003), 591–609.CrossRefGoogle Scholar
Krishnapur, M., Kurlberg, P. and Wigman, I., Nodal length fluctuations for arithmetic random waves, Ann. Math. 177 (2013), 699–737.CrossRefGoogle Scholar
Müller, W., Lattice points in large convex bodies, Monatsh. fur Math. 128(4) (1999), 315–330.Google Scholar
Sogge, C. D., Fourier Integrals in Classical analysis, Volume 210, (Cambridge University Press, 2017).CrossRefGoogle Scholar
Stein, E. M., Harmonic analysis: real-Variable methods, orthogonality, and Oscillatory integrals, Volume 3, (Princeton University Press, 1993).Google Scholar
Tomas, P., A restriction theorem for the Fourier transform, Bull. Amer. Math. Soc. 81 (1975), 477–478.CrossRefGoogle Scholar
Zygmund, A., On Fourier coefficients and transforms of functions of two variables, Stud. Math. 50(2) (1974), 189–201.CrossRefGoogle Scholar


