Hostname: page-component-84b7d79bbc-tsvsl Total loading time: 0 Render date: 2024-07-25T14:40:17.242Z Has data issue: false hasContentIssue false
  • English
  • Français

An algebraic filtration of H*(MO;ℤ2)

Published online by Cambridge University Press:  20 January 2009

Stanley O. Kochman
Stanley O. Kochman
Affiliation:
Department of MathematicsThe University of Western OntarioLondon, Ontario, CanadaN6A 5B7
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 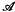2* denote the dual of the mod two Steenrod algebra. In [5] an algebraic filtration B*(n) of H*(BO; ℤ2) was constructed such that each B*(n) is a bipolynomial sub Hopf algebra and sub 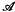2*-comodule of H*(BO; ℤ2). In Lemma 3.1 we prove that the Thom isomorphism determines a corresponding filtration of H*(MO;ℤ2) by polynomial subalgebras and sub 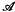2*-comodules M*(n). Let 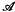(n) denote the subalgebra of 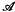2 generated by Sq2k, 0 ≦ k < n, and let 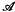*(n) be its dual, a quotient Hopf algebra of 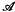2*. In Section 3 we construct a polynomial algebra and 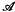*(n)-comodule R(n) such that M*(n)≃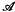2*□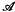*(n)R(n) as algebras and 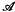2*-comodules. Here □ denotes the cotensor product defined in [9, §2]. Dually it will follow that M*(n) has a sub 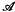(n)-module and subcoalgebra T(n) such that M*(n)≃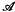2⊗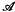n)T(n) as coalgebras and 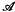2-modules. We also show that M*(n) can not be realised as the homology of a spectrum for n≧4. Of course M*(0)=H*(MO;ℤ2), M*(1)=H*(MSO;ℤ2), M*(2)=H* (MSpin;ℤ2) and M*(3)=H*(MO<8>;ℤ2). Moreover, it follows from [4; Thm. 2.10, Cor. 2.11] that M*(n)=Images[H*(MO<ϕ(n)>;ℤ2)→H*(MO;ℤ2)] and M*(n) ≃ Image [H*(MO;ℤ2)→ H*(MO<ϕ(n)>;ℤ2)]. Here MO<k> id the Thom spectrum of BO<k>, the (k−1)-connected covering of BO, and ϕ(n)=8s + 2t where n = 4s + t, 0≦t≦3. In Section 4 we sketch the odd primary analogue—a filtration pM*(n) of H*(MUp, 0;ℤp) for p an odd prime. MUp, 0 is the Thom spectrum of the (2p-3)-connected factor of the Adams splitting [2] of BU(p).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 26 , Issue 3 , October 1983 , pp. 313 - 317
Copyright
Copyright © Edinburgh Mathematical Society 1983

References

REFERENCES

1.Adams, J. F., On the non-existence of elements of Hopf invariant one, Annals of Math. 72 (1960), 20–104.CrossRefGoogle Scholar
2.Adams, J. F., Lectures on generalised cohomology, Category Theory, Homology Theory and their Applications III, Battelle Institute Conference, Seattle, Wash., 1968, vol. 3 (Lecture Notes in Math., no. 99, Springer-Verlag, Berlin, 1969), 1–138.Google Scholar
3.Brown, E. H. and Peterson, F. P., H*(MO) as an algebra over the Steenrod algebra, Conference on Homotopy Theory, Northwestern U., Evanston, Ill., 1974 (Serie Notas de Matemática y Simposia, Sociedad Matemática Mexicana, 1975), 11–19.Google Scholar
4.Kane, R. M., Operations in connective K-theory (Memoirs Amer. Math. Soc. no. 254, 1981).Google Scholar
5.Kochman, S. O., An algebraic filtration of H*BO, Proceedings of the Northwestern Homotopy Theory Conference (Contemporary Math. Series of the Amer. Math. Soc. 19, (1983)), 115–144.CrossRefGoogle Scholar
6.Liulevicius, A., The factorization of cyclic reduced powers by secondary cohomology operations (Memoirs Amer. Math. Soc. No. 42, 1962).CrossRefGoogle Scholar
7.Liulevtcius, A., A proof of Thom's theorem, Comment. Math. Helv. 37 (1962), 121–131.Google Scholar
8.Milnor, J. W. and Moore, J. C., On the structure of Hopf algebras, Annals of Math. 81 (1965), 211–264.Google Scholar
10.Penoelley, D. J., The -algebra structure of Thom spectra: MSO as an example, Current Trends in Algebraic Topology (Can. Math. Soc. Conference Proceedings 2, Part 1, (1982)), 511–513.Google Scholar
11.Pengelley, D. J., H *,(MO<8>;z2) is an extended 2-coalgebra, Proc. Amer. Math. Soc. 87 (1983), 355–356.Google Scholar
12.Thom, R., Quelques propriétés globales des variétés differentiables, Comm. Math. Helv. 28 (1954), 17–86.CrossRefGoogle Scholar