A set 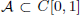is shy or Haar null (in the sense of Christensen) if there exists a Borel set 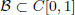and a Borel probability measure μ on C[0, 1] such that 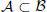and 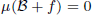for all f ∈ C[0, 1]. The complement of a shy set is called a prevalent set. We say that a set is Haar ambivalent if it is neither shy nor prevalent.

The main goal of the paper is to answer the following question: what can we say about the topological properties of the level sets of the prevalent/non-shy many f ∈ C[0, 1]?

The classical Bruckner–Garg theorem characterizes the level sets of the generic (in the sense of Baire category) f ∈ C[0, 1] from the topological point of view. We prove that the functions f ∈ C[0, 1] for which the same characterization holds form a Haar ambivalent set.

In an earlier paper, Balka et al. proved that the functions f ∈ C[0, 1] for which positively many level sets with respect to the Lebesgue measure λ are singletons form a non-shy set in C[0, 1]. The above result yields that this set is actually Haar ambivalent. Now we prove that the functions f ∈ C[0, 1] for which positively many level sets with respect to the occupation measure λ ◦ f–1 are not perfect form a Haar ambivalent set in C[0, 1].

We show that for the prevalent f ∈ C[0, 1] for the generic y ∈ f([0, 1]) the level set f–1(y) is perfect. Finally, we answer a question of Darji and White by showing that the set of functions f ∈ C[0, 1] for which there exists a perfect set Pf ⊂ [0, 1] such that fʹ(x) = ∞ for all x ∈ Pf is Haar ambivalent.