Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-17T02:30:00.503Z Has data issue: false hasContentIssue false
  • English
  • Français

A Chebyshev-type alternation theorem for best approximation by a sum of two algebras

Part of: Approximations and expansions Normed linear spaces and Banach spaces; Banach lattices Linear function spaces and their duals

Published online by Cambridge University Press:  01 September 2023

Aida KH. Asgarova ,
Ali A. Huseynli  and
Vugar E. Ismailov
Aida KH. Asgarova
Affiliation:
Department of Function Theory, Institute of Mathematics and Mechanics, Baku, AZ1141, Azerbaijan (aidaasgarova@gmail.com; aidaasgarova@gmail.com)
Ali A. Huseynli
Affiliation:
Department of Function Theory, Institute of Mathematics and Mechanics, Baku, AZ1141, Azerbaijan (aidaasgarova@gmail.com; aidaasgarova@gmail.com) Department of Mathematics, Khazar University, Baku, AZ1096, Azerbaijan (alihuseynli@gmail.com)
Vugar E. Ismailov
Affiliation:
Department of Function Theory, Institute of Mathematics and Mechanics, Baku, AZ1141, Azerbaijan (aidaasgarova@gmail.com; aidaasgarova@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a compact metric space, C(X) be the space of continuous real-valued functions on X and 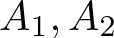$A_{1},A_{2}$ be two closed subalgebras of C(X) containing constant functions. We consider the problem of approximation of a function 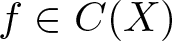$f\in C(X)$ by elements from 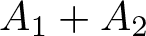$A_{1}+A_{2}$. We prove a Chebyshev-type alternation theorem for a function 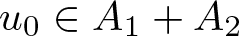$u_{0} \in A_{1}+A_{2}$ to be a best approximation to f.

Keywords

Chebyshev alternation theorembest approximationboltweak* convergenceBanach–Alaoglu theorem

MSC classification

Primary: 41A30: Approximation by other special function classes 41A50: Best approximation, Chebyshev systems 46B50: Compactness in Banach (or normed) spaces 46E15: Banach spaces of continuous, differentiable or analytic functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 971 - 978
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I., On functions of three variables, (Russian), Dokl. Akad. Nauk SSSR 114(2) (1957), 679–681. English transl. in Amer. Math. Soc. Transl. 28 (1963), 51–54.Google Scholar
Asgarova, A. K. and Ismailov, V. E., A Chebyshev-type theorem characterizing best approximation of a continuous function by elements of the sum of two algebras, (Russian, Mat. Zametki 109(1) (2021), 19–26).Google Scholar
Brosowski, B. and da Silva, A. R., A general alternation theorem, approximation theory (Memphis, TN, 1991), 137–150. Lecture Notes in Pure and Applied Mathematics, Volume 138 (Dekker, New York, 1992).Google Scholar
Buck, R. C., Alternation theorems for functions of several variables, J. Approx. Theory 1(3) (1968), 325–334.CrossRefGoogle Scholar
Cowsik, R. C., Klopotowski, A. and Nadkarni, M. G., When is ${f(x,y)=u(x)+v(y)}$?, Proc. Indian Acad. Sci. Math. Sci. 109(1) (1999), 57–64.CrossRefGoogle Scholar
Diliberto, S. P. and Straus, E. G., On the approximation of a function of several variables by the sum of functions of fewer variables, Pacific J. Math. 1(2) (1951), 195–210.CrossRefGoogle Scholar
Herman, R. A., Quotients of metric spaces (A.B. Grinnell College, 1966).Google Scholar
Ismailov, V. E., Ridge functions and applications in neural networks. Mathematical Surveys and Monographs 263, , (American Mathematical Society, 2021).CrossRefGoogle Scholar
Havinson, S. J., A Chebyshev theorem for the approximation of a function of two variables by sums of the type $\varphi \left( {x}\right) +\psi \left( {y}\right)$, Izv. Acad. Nauk. SSSR Ser. Mat. 33(3) (1969), 650–666. English transl. in Math. USSR Izv. 3 (1969), 617–632.Google Scholar
Khavinson, S. Y., Best approximation by linear superpositions (approximate nomography), Translated from the Russian manuscript, Khavinson, D. (ed) Translations of mathematical monographs, Volume 159, (American Mathematical Society, Providence, RI, 1997).Google Scholar
Light, W. A. and Cheney, E. W., On the approximation of a bivariate function by the sum of univariate functions, J. Approx. Theory 29(4) (1980), 305–322.CrossRefGoogle Scholar
Marshall, D. E. and O’Farrell, A. G., Uniform approximation by real functions, Fund. Math. 104(3) (1979), 203–211.CrossRefGoogle Scholar
Marshall, D. E. and O’Farrell, A. G., Approximation by a sum of two algebras. The lightning bolt principle, J. Funct. Anal. 52(3) (1983), 353–368.CrossRefGoogle Scholar
Natanson, I. P., Constructive function theory, Vol. I. Uniform approximation, Obolensky, A. N. (ed), Translated from the Russian, (Frederick Ungar Publishing Co., New York, 1964).Google Scholar
Rudin, W., Functional analysis, McGraw-Hill Series in Higher Mathematics, (McGraw-Hill Book Co, 1973).Google Scholar
Singer, I.. The theory of best approximation and functional analysis, Conference Board of the Mathematical Sciences Regional Conference Series in Applied Mathematics, No. 13. Society for Industrial and Applied Mathematics, Philadelphia, PA, (SIAM Publications Library, 1974).Google Scholar
Sternfeld, Y., Uniform separation of points and measures and representation by sums of algebras, Israel J. Math. 55(3) (1986), 350–362.CrossRefGoogle Scholar
Stone, A. H., Metrizability of decomposition spaces, Proc. Amer. Math. Soc. 7(4) (1956), 690–700.CrossRefGoogle Scholar
Stone, M. H., Applications of the theory of Boolean rings to gneral topology, Trans. Amer. Math. Soc. 41(3) (1937), 375–481.CrossRefGoogle Scholar
Stone, M. H., The generalized Weierstrass approximation theorem, Math. Mag. 21(4) (1948), .CrossRefGoogle Scholar