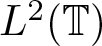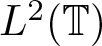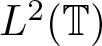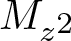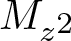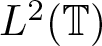1. Introduction
Suppose T is a bounded linear operator on a separable Hilbert space ![]() $\mathcal{H}$. Then, the commutant of T is usually denoted by
$\mathcal{H}$. Then, the commutant of T is usually denoted by ![]() $\{T\}^\prime$ and defined by
$\{T\}^\prime$ and defined by ![]() $\{T\}^\prime :=\{S\in \mathcal{B}(\mathcal{H}): ST=TS\}$, where
$\{T\}^\prime :=\{S\in \mathcal{B}(\mathcal{H}): ST=TS\}$, where ![]() $\mathcal{B}(\mathcal{H})$ is the space of all bounded linear operators on
$\mathcal{B}(\mathcal{H})$ is the space of all bounded linear operators on ![]() $\mathcal{H}$. Given a bounded linear operator T, it is always interesting to find the commutant
$\mathcal{H}$. Given a bounded linear operator T, it is always interesting to find the commutant ![]() $\{T\}^\prime$ since it plays an important role in determining the structure of the operator. Another strong reason for identifying the commutant of an operator T is to recognize all reducing subspaces of T. In this direction, there are various nice works available in the literature, specially for analytic multiplication operators on some well-known function spaces like the Hardy space, the Bergman space and also for reproducing kernel Hilbert spaces. The details can be found in [Reference Douglas, Putinar and Wang13, Reference Guo and Huang23, Reference Guo, Sun, Zheng and Zhong24, Reference Stessin and Zhu35, Reference Zhu39].
$\{T\}^\prime$ since it plays an important role in determining the structure of the operator. Another strong reason for identifying the commutant of an operator T is to recognize all reducing subspaces of T. In this direction, there are various nice works available in the literature, specially for analytic multiplication operators on some well-known function spaces like the Hardy space, the Bergman space and also for reproducing kernel Hilbert spaces. The details can be found in [Reference Douglas, Putinar and Wang13, Reference Guo and Huang23, Reference Guo, Sun, Zheng and Zhong24, Reference Stessin and Zhu35, Reference Zhu39].
Let ![]() $\mathbb{D}=\{z\in \mathbb{C}:~|z| \lt 1\}$ denote the unit disc in the complex plane and
$\mathbb{D}=\{z\in \mathbb{C}:~|z| \lt 1\}$ denote the unit disc in the complex plane and ![]() $\mathbb{T}=\{z\in \mathbb{C}:~|z|=1\}$ be the unit circle. Let us denote by
$\mathbb{T}=\{z\in \mathbb{C}:~|z|=1\}$ be the unit circle. Let us denote by ![]() $L^2 (\mathbb{T})$ (or simply L 2) the space of all square-integrable functions over the unit circle
$L^2 (\mathbb{T})$ (or simply L 2) the space of all square-integrable functions over the unit circle ![]() $\mathbb{T}$. The Banach space of all essentially bounded functions on the unit circle
$\mathbb{T}$. The Banach space of all essentially bounded functions on the unit circle ![]() $\mathbb{T}$ is denoted by
$\mathbb{T}$ is denoted by ![]() $L^\infty(\mathbb{T})$ (or
$L^\infty(\mathbb{T})$ (or ![]() $L^\infty$ in short). Therefore, if
$L^\infty$ in short). Therefore, if ![]() $f\in L^2(\mathbb{T})$, then the function f can be expressed as:
$f\in L^2(\mathbb{T})$, then the function f can be expressed as:
 \begin{equation*}f(z)=\sum_{n=-\infty}^{\infty}\hat{f}(n)z^n,\end{equation*}
\begin{equation*}f(z)=\sum_{n=-\infty}^{\infty}\hat{f}(n)z^n,\end{equation*} where  $\hat{f}(n)$ denotes the nth Fourier coefficient of f and
$\hat{f}(n)$ denotes the nth Fourier coefficient of f and  $\sum\limits_{n=-\infty}^{\infty}|\hat{f}(n)|^2 \lt \infty$. For
$\sum\limits_{n=-\infty}^{\infty}|\hat{f}(n)|^2 \lt \infty$. For ![]() $\phi\in L^{\infty}$, let Mϕ denote the multiplication operator on L 2 defined as:
$\phi\in L^{\infty}$, let Mϕ denote the multiplication operator on L 2 defined as: ![]() $M_{\phi}(f)=\phi f,\quad f\in L^2.$
$M_{\phi}(f)=\phi f,\quad f\in L^2.$
Recall that the classical Hardy space over the unit disc ![]() $\mathbb{D}$ is denoted by
$\mathbb{D}$ is denoted by ![]() $H^2(\mathbb{D})$ and defined by:
$H^2(\mathbb{D})$ and defined by:
 \begin{equation*}
H^2(\mathbb{D}):=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n:~\|f\|_{H^2(\mathbb{D})}^2:=\sum_{n=0}^{\infty}|a_n|^2,~z\in \mathbb{D},~a_n\in \mathbb{C}\Big\}.
\end{equation*}
\begin{equation*}
H^2(\mathbb{D}):=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n:~\|f\|_{H^2(\mathbb{D})}^2:=\sum_{n=0}^{\infty}|a_n|^2,~z\in \mathbb{D},~a_n\in \mathbb{C}\Big\}.
\end{equation*} For ![]() $f\in H^2(\mathbb{D})$, the non-tangential boundary limit (radial limit)
$f\in H^2(\mathbb{D})$, the non-tangential boundary limit (radial limit) ![]() $\tilde{f}(e^{i\theta})=\lim_{r\to 1-}f(re^{i\theta})$ exists almost everywhere on
$\tilde{f}(e^{i\theta})=\lim_{r\to 1-}f(re^{i\theta})$ exists almost everywhere on ![]() $\mathbb{T}$ [Reference Fricain and Mashreghi14, Reference Fricain and Mashreghi15, Reference Martínez-Avendaño and Rosenthal28]. Therefore,
$\mathbb{T}$ [Reference Fricain and Mashreghi14, Reference Fricain and Mashreghi15, Reference Martínez-Avendaño and Rosenthal28]. Therefore, ![]() $H^2(\mathbb{D})$ can be embedded isometrically as a closed subspace of
$H^2(\mathbb{D})$ can be embedded isometrically as a closed subspace of ![]() $L^2(\mathbb{T})$ by identifying
$L^2(\mathbb{T})$ by identifying ![]() $H^2(\mathbb{D})$ through the non-tangential boundary limits of the
$H^2(\mathbb{D})$ through the non-tangential boundary limits of the ![]() $H^2(\mathbb{D})$ functions. In other words, we can recognize the Hardy space
$H^2(\mathbb{D})$ functions. In other words, we can recognize the Hardy space ![]() $H^2(\mathbb{D})$ as a closed subspace of
$H^2(\mathbb{D})$ as a closed subspace of ![]() $L^2(\mathbb{T})$, say H 2, consisting of L 2 functions having negative Fourier coefficients zero. We denote by
$L^2(\mathbb{T})$, say H 2, consisting of L 2 functions having negative Fourier coefficients zero. We denote by ![]() $H^{\infty}$ the space of all bounded analytic functions on
$H^{\infty}$ the space of all bounded analytic functions on ![]() $\mathbb{D}$ that can be identified with a closed subspace of
$\mathbb{D}$ that can be identified with a closed subspace of ![]() $L^{\infty}$, that is
$L^{\infty}$, that is ![]() $H^\infty:= L^\infty \cap H^2$. An inner function θ is an element in
$H^\infty:= L^\infty \cap H^2$. An inner function θ is an element in ![]() $H^\infty$ such that
$H^\infty$ such that ![]() $|\theta | =1$ almost everywhere on
$|\theta | =1$ almost everywhere on ![]() $\mathbb{T}$. For
$\mathbb{T}$. For ![]() $\phi\in L^{\infty}$, define the Toeplitz operator
$\phi\in L^{\infty}$, define the Toeplitz operator ![]() $T_{\phi}:H^2\to H^2$ by
$T_{\phi}:H^2\to H^2$ by ![]() $T_{\phi}f=P(\phi f),$ where P is the orthogonal projection from L 2 onto H 2. Recall that the unilateral shift S on H 2 is defined by
$T_{\phi}f=P(\phi f),$ where P is the orthogonal projection from L 2 onto H 2. Recall that the unilateral shift S on H 2 is defined by ![]() $Sf(z)=zf(z), f\in H^2$, a restriction of the bilateral shift Mz on L 2. A well-known theorem due to Beurling characterizes all the S-invariant subspaces of H 2. In other words, any S-invariant subspace of H 2 is of the form
$Sf(z)=zf(z), f\in H^2$, a restriction of the bilateral shift Mz on L 2. A well-known theorem due to Beurling characterizes all the S-invariant subspaces of H 2. In other words, any S-invariant subspace of H 2 is of the form ![]() $\theta H^2$, where θ is an inner function. For any inner function θ, the model space Kθ is defined by
$\theta H^2$, where θ is an inner function. For any inner function θ, the model space Kθ is defined by ![]() $K_\theta := H^2\ominus \theta H^2$, which is
$K_\theta := H^2\ominus \theta H^2$, which is ![]() $S^*$ invariant. For more on model spaces and related stuff, we refer the reader to [Reference Fricain and Mashreghi14, Reference Fricain and Mashreghi15, Reference Garcia, Mashreghi and Ross17, Reference Martínez-Avendaño and Rosenthal28].
$S^*$ invariant. For more on model spaces and related stuff, we refer the reader to [Reference Fricain and Mashreghi14, Reference Fricain and Mashreghi15, Reference Garcia, Mashreghi and Ross17, Reference Martínez-Avendaño and Rosenthal28].
The commutant of S in H 2 is ![]() $\{T_{\phi}:~\phi\in H^{\infty}\}$ and the commutant of Mz in L 2 is
$\{T_{\phi}:~\phi\in H^{\infty}\}$ and the commutant of Mz in L 2 is ![]() $\{M_{\phi}:~\phi\in L^{\infty}\}$ [Reference Martínez-Avendaño and Rosenthal28, Reference Radjavi and Rosenthal32]. In general, it is highly non-trivial to describe the commutant of a given bounded linear operator. In this direction, the commutant of more general shift operators and Toeplitz operators in various function spaces has been studied by many authors [Reference Abkar, Cao and Zhu1, Reference Cowen6–Reference Cowen and Douglas8, Reference Deddens and Wong12, Reference Khani Robati25, Reference Khani Robati and Vaezpour26, Reference Nordgren30, Reference Seddighi and Vaezpour33].
$\{M_{\phi}:~\phi\in L^{\infty}\}$ [Reference Martínez-Avendaño and Rosenthal28, Reference Radjavi and Rosenthal32]. In general, it is highly non-trivial to describe the commutant of a given bounded linear operator. In this direction, the commutant of more general shift operators and Toeplitz operators in various function spaces has been studied by many authors [Reference Abkar, Cao and Zhu1, Reference Cowen6–Reference Cowen and Douglas8, Reference Deddens and Wong12, Reference Khani Robati25, Reference Khani Robati and Vaezpour26, Reference Nordgren30, Reference Seddighi and Vaezpour33].
For a finite Blaschke product B, let MB be the operator of multiplication by B in ![]() $L^2(\mathbb{T})$. The commutants of finite Blaschke product Toeplitz operators TB are ‘well known’ for the Hardy space H 2 [Reference Cowen6]. So in some sense, we can say that these are the ‘same’ operators that commute with MB on other Hilbert spaces. In 2015, Cowen and Wahl [Reference Cowen and Wahl5] gave a detailed independent description of the operators on the Hilbert space
$L^2(\mathbb{T})$. The commutants of finite Blaschke product Toeplitz operators TB are ‘well known’ for the Hardy space H 2 [Reference Cowen6]. So in some sense, we can say that these are the ‘same’ operators that commute with MB on other Hilbert spaces. In 2015, Cowen and Wahl [Reference Cowen and Wahl5] gave a detailed independent description of the operators on the Hilbert space ![]() $\mathcal{H}$ of analytic functions defined on
$\mathcal{H}$ of analytic functions defined on ![]() $\mathbb{D}$ that commutes with MB. Abkar et al. [Reference Abkar, Cao and Zhu1] gives a complete description of the commutant of
$\mathbb{D}$ that commutes with MB. Abkar et al. [Reference Abkar, Cao and Zhu1] gives a complete description of the commutant of ![]() $M_{z^n}$ on a family of analytic function spaces on
$M_{z^n}$ on a family of analytic function spaces on ![]() $\mathbb{D}$, which include the Bergman space, the Hardy space and the Dirichlet space. Note that these are shift operators of higher multiplicity, in other words, special multiplication operator by particular finite Blaschke. More explicitly, the authors in [Reference Abkar, Cao and Zhu1] provide the description regarding the commutant of
$\mathbb{D}$, which include the Bergman space, the Hardy space and the Dirichlet space. Note that these are shift operators of higher multiplicity, in other words, special multiplication operator by particular finite Blaschke. More explicitly, the authors in [Reference Abkar, Cao and Zhu1] provide the description regarding the commutant of ![]() $M_{z^n}$ by identifying with n copies of the multiplier algebra of the underlying function spaces. Recently, Gallardo and Partington [Reference Gallardo-Gutiérrez and Partington16] provide a characterization of the commutant of TB extending the work on the weighted Bergman spaces.
$M_{z^n}$ by identifying with n copies of the multiplier algebra of the underlying function spaces. Recently, Gallardo and Partington [Reference Gallardo-Gutiérrez and Partington16] provide a characterization of the commutant of TB extending the work on the weighted Bergman spaces.
Our primary goal in this paper is to characterize the commutant of MB independently in the ![]() $L^2(\mathbb{T})$-space and obtain a detailed description of the commutant in terms of
$L^2(\mathbb{T})$-space and obtain a detailed description of the commutant in terms of ![]() $L^\infty$-functions. As a consequence, by using the precise structure of the commutator, we will obtain some applications towards characterizing conjugations in
$L^\infty$-functions. As a consequence, by using the precise structure of the commutator, we will obtain some applications towards characterizing conjugations in ![]() $L^2(\mathbb{T})$.
$L^2(\mathbb{T})$.
Now, the study of conjugations and complex symmetric operators has become a widely interested research area because of its significance in the fields of operator theory, complex analysis and physics. Recently, several authors have been interested in non-Hermitian quantum mechanics and the spectral analysis of certain complex symmetric operators (for more details, see [Reference Bender, Fring, Günther and Jones2, Reference Garcia, Prodan and Putinar18]). One of the motivations for studying conjugations comes from the study of complex symmetric operators. The study of complex symmetric (in short, C-symmetric) operators was initiated by Garcia et al. [Reference Garcia and Putinar19–Reference Garcia and Wogen22]. Technically speaking, a conjugation C is an antilinear and isometric involution on ![]() $\mathcal{H}$. In other words, a conjugate-linear operator
$\mathcal{H}$. In other words, a conjugate-linear operator ![]() $C:\mathcal{H} \to \mathcal{H}$ is said to be a conjugation if it satisfies the following two conditions:
$C:\mathcal{H} \to \mathcal{H}$ is said to be a conjugation if it satisfies the following two conditions:
(a)
 $C^2 =I_{\mathcal{H}}$, (the identity operator on
$C^2 =I_{\mathcal{H}}$, (the identity operator on  $\mathcal{H}$);
$\mathcal{H}$);(b)
 $\langle Cf,Cg \rangle = \langle g,f \rangle , \forall f,g \in \mathcal{H}$.
$\langle Cf,Cg \rangle = \langle g,f \rangle , \forall f,g \in \mathcal{H}$.
It is interesting to observe that the conjugation is a straightforward generalization of the conjugate-linear map ![]() $z\mapsto \bar{z}$ on the one-dimensional Hilbert space
$z\mapsto \bar{z}$ on the one-dimensional Hilbert space ![]() $\mathbb{C}$. Moreover, we can also interpret conjugation as a special kind of antilinear operator and note that the antilinear operator is the only type of nonlinear operator that is important in the field of quantum mechanics (for more details, see [Reference Messiah29, Reference Sobrino34, Reference Weinberg38]). In this connection, it is remarkable to mention that Garcia and Putinar have shown in [Reference Garcia and Putinar19] that for any given conjugation C on
$\mathbb{C}$. Moreover, we can also interpret conjugation as a special kind of antilinear operator and note that the antilinear operator is the only type of nonlinear operator that is important in the field of quantum mechanics (for more details, see [Reference Messiah29, Reference Sobrino34, Reference Weinberg38]). In this connection, it is remarkable to mention that Garcia and Putinar have shown in [Reference Garcia and Putinar19] that for any given conjugation C on ![]() $\mathcal{H}$, there exists an orthonormal basis
$\mathcal{H}$, there exists an orthonormal basis ![]() $\{e_n: n\in \mathbb{N}_0\}$ such that
$\{e_n: n\in \mathbb{N}_0\}$ such that ![]() $Ce_n=e_n$ for all
$Ce_n=e_n$ for all ![]() $n\in \mathbb{N}_0$, where
$n\in \mathbb{N}_0$, where ![]() $\mathbb{N}_0$ denotes the set of all non-negative integers.
$\mathbb{N}_0$ denotes the set of all non-negative integers.
Definition 1.1. An operator ![]() $T\in \mathcal{B}(\mathcal{H})$ is called C-symmetric if there exists a conjugation C on
$T\in \mathcal{B}(\mathcal{H})$ is called C-symmetric if there exists a conjugation C on ![]() $\mathcal{H}$ such that
$\mathcal{H}$ such that ![]() $CTC=T^*$, where
$CTC=T^*$, where ![]() $T^*$ is the adjoint of T. If T is C-symmetric for some conjugation C, then T is called complex symmetric.
$T^*$ is the adjoint of T. If T is C-symmetric for some conjugation C, then T is called complex symmetric.
The class of complex symmetric operators includes all normal operators, Hankel operators, truncated Toeplitz operators and Volterra integration operators. For more on complex symmetric operators and related topics, including historical comments, we refer the reader to [Reference Garcia and Putinar19–Reference Garcia and Wogen22, Reference Ko and Lee27, Reference Waleed Noor37] and the references cited therein. We denote by ![]() $\mathcal{B}A(\mathcal{H})$ the space of all bounded antilinear operators on
$\mathcal{B}A(\mathcal{H})$ the space of all bounded antilinear operators on ![]() $\mathcal{H}$. Recall that for
$\mathcal{H}$. Recall that for ![]() $A \in \mathcal{B}A(\mathcal{H})$ there exists a unique antilinear operator
$A \in \mathcal{B}A(\mathcal{H})$ there exists a unique antilinear operator ![]() $A^\sharp$, known as the antilinear adjoint of A, defined by the equality:
$A^\sharp$, known as the antilinear adjoint of A, defined by the equality:
It is important to observe that ![]() $C^\sharp=C$ for any conjugation C,
$C^\sharp=C$ for any conjugation C, ![]() $(AB)^{\sharp}=B^*A^{\sharp}$ and
$(AB)^{\sharp}=B^*A^{\sharp}$ and ![]() $(BA)^{\sharp}=A^{\sharp}B^*$ for
$(BA)^{\sharp}=A^{\sharp}B^*$ for ![]() $A \in \mathcal{B}A(\mathcal{H})$,
$A \in \mathcal{B}A(\mathcal{H})$, ![]() $B\in\mathcal{B}(\mathcal{H})$ (see e.g., [Reference Câmara, Kliś-Garlicka and Ptak9]).
$B\in\mathcal{B}(\mathcal{H})$ (see e.g., [Reference Câmara, Kliś-Garlicka and Ptak9]).
Two natural conjugations J and ![]() $J^\star$ on
$J^\star$ on ![]() $L^2(\mathbb{T})$ are defined as follows:
$L^2(\mathbb{T})$ are defined as follows:
It is important to observe that the conjugation J intertwines the operators Mz and ![]() $M_{\bar{z}}$. In other words Mz is J-symmetric, that is
$M_{\bar{z}}$. In other words Mz is J-symmetric, that is ![]() $JM_zJ =M_{\bar{z}}$. Moreover,
$JM_zJ =M_{\bar{z}}$. Moreover, ![]() $JH^2 = \overline{H^2}$, that is J maps an analytic function to a co-analytic function. On the other hand, the conjugation
$JH^2 = \overline{H^2}$, that is J maps an analytic function to a co-analytic function. On the other hand, the conjugation ![]() $J^\star$ has different nature in comparison to J. For example,
$J^\star$ has different nature in comparison to J. For example, ![]() $J^\star M_z =M_zJ^\star$ and it preserves the Hardy space H 2. Furthermore, it is worth mentioning that the map
$J^\star M_z =M_zJ^\star$ and it preserves the Hardy space H 2. Furthermore, it is worth mentioning that the map ![]() $J^\star$ has a connection with model spaces [Reference Cima, Garcia, Ross and Wogen4] and Hankel operators [Reference Martínez-Avendaño and Rosenthal28]. In this connection, recently, Câmara-Garlicka-Łanucha-Ptak raised a natural question in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10] regarding the characterization of conjugations that possess similar kinds of properties as J and
$J^\star$ has a connection with model spaces [Reference Cima, Garcia, Ross and Wogen4] and Hankel operators [Reference Martínez-Avendaño and Rosenthal28]. In this connection, recently, Câmara-Garlicka-Łanucha-Ptak raised a natural question in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10] regarding the characterization of conjugations that possess similar kinds of properties as J and ![]() $J^\star$. More precisely, they characterize the class of conjugations that commute with Mz and also classify the class of conjugations intertwining the operators Mz and
$J^\star$. More precisely, they characterize the class of conjugations that commute with Mz and also classify the class of conjugations intertwining the operators Mz and ![]() $M_{\bar{z}}$ in scalar-valued
$M_{\bar{z}}$ in scalar-valued ![]() $L^2(\mathbb{T})$ space [Reference Câmara, Kliś-Garlicka and Ptak9, Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10] as well as in vector-valued
$L^2(\mathbb{T})$ space [Reference Câmara, Kliś-Garlicka and Ptak9, Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10] as well as in vector-valued ![]() $L^2(\mathcal{H})$ space [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak11] over the unit circle
$L^2(\mathcal{H})$ space [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak11] over the unit circle ![]() $\mathbb{T}$. Therefore it is natural to study the complex symmetry of MB in
$\mathbb{T}$. Therefore it is natural to study the complex symmetry of MB in ![]() $L^2(\mathbb{T})$, where B is a finite Blaschke product. To this end, we begin with the study of the complex symmetry of
$L^2(\mathbb{T})$, where B is a finite Blaschke product. To this end, we begin with the study of the complex symmetry of ![]() $M_{z^2}$ in
$M_{z^2}$ in ![]() $L^2(\mathbb{T})$ since it will help to complement the study of MB. It is important to observe that the commutant of Mz is properly contained in the commutant of
$L^2(\mathbb{T})$ since it will help to complement the study of MB. It is important to observe that the commutant of Mz is properly contained in the commutant of ![]() $M_{z^2}$ and also the class of conjugations intertwining the operators
$M_{z^2}$ and also the class of conjugations intertwining the operators ![]() $M_{z^2}$,
$M_{z^2}$, ![]() $M_{\bar{z}^2}$ in L 2 is bigger than the class of conjugations intertwining the operators Mz,
$M_{\bar{z}^2}$ in L 2 is bigger than the class of conjugations intertwining the operators Mz, ![]() $M_{\bar{z}}$ in L 2. In this direction, we begin with the following two questions.
$M_{\bar{z}}$ in L 2. In this direction, we begin with the following two questions.
Question 1. Which class of conjugations commute with ![]() $M_{z^2}$ in
$M_{z^2}$ in ![]() $L^2(\mathbb{T})$ but not with Mz
$L^2(\mathbb{T})$ but not with Mz
Question 2. Which class of conjugations makes the operator ![]() $M_{z^2}$ complex symmetric in
$M_{z^2}$ complex symmetric in ![]() $L^2(\mathbb{T}) $ but does not possess the same characteristic with Mz?
$L^2(\mathbb{T}) $ but does not possess the same characteristic with Mz?
Later in ![]() $\S$ 4, we provide appropriate answers to the above questions. Note that our work mainly focus on the case for
$\S$ 4, we provide appropriate answers to the above questions. Note that our work mainly focus on the case for ![]() $only~M_{z^2}$commuting conjugations and
$only~M_{z^2}$commuting conjugations and ![]() $M_{z^2},M_{\bar{z}^2}$-intertwining (but not
$M_{z^2},M_{\bar{z}^2}$-intertwining (but not ![]() $M_{z},M_{\bar{z}}$-intertwining ) conjugations throughout this article. Note that the operator Mz in
$M_{z},M_{\bar{z}}$-intertwining ) conjugations throughout this article. Note that the operator Mz in ![]() $\mathbb{C}^n$-valued L 2 space over
$\mathbb{C}^n$-valued L 2 space over ![]() $\mathbb{T}$ is unitary equivalent to MB in the classical L 2 space over
$\mathbb{T}$ is unitary equivalent to MB in the classical L 2 space over ![]() $\mathbb{T}$, where B is a finite Blaschke product of degree n. Since the characterization of the class of conjugations that commute with Mz and also the class of conjugations intertwining the operators Mz and
$\mathbb{T}$, where B is a finite Blaschke product of degree n. Since the characterization of the class of conjugations that commute with Mz and also the class of conjugations intertwining the operators Mz and ![]() $M_{\bar{z}}$ have been studied in the vector-valued
$M_{\bar{z}}$ have been studied in the vector-valued ![]() $L^2(\mathcal{H})$ space in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak11], then in some sense such characterization results regarding
$L^2(\mathcal{H})$ space in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak11], then in some sense such characterization results regarding ![]() $M_{z^2}$ can also be given in
$M_{z^2}$ can also be given in ![]() $L^2(\mathbb{T})$ space. But the novelty of our characterization results lies in the fact that we have the precise structure of such conjugations, which cannot be achieved easily using the above-mentioned unitary equivalence. Moreover, a further benefit of our description is that one can independently classify the conjugations in
$L^2(\mathbb{T})$ space. But the novelty of our characterization results lies in the fact that we have the precise structure of such conjugations, which cannot be achieved easily using the above-mentioned unitary equivalence. Moreover, a further benefit of our description is that one can independently classify the conjugations in ![]() $L^2(\mathbb{T})$, which do not possess similar properties with Mz.
$L^2(\mathbb{T})$, which do not possess similar properties with Mz.
In other words, the precise (or major) contributions in this article are the following:
• We identify the commutant of MB in L 2, where B is a finite Blaschke product.
• Using the above characterization, we classify the set of conjugations that commute with
 $M_{z^2}$ but fail to commute with Mz.
$M_{z^2}$ but fail to commute with Mz.• Class of conjugations intertwining the operators
 $M_{z^2}$ and
$M_{z^2}$ and  $M_{\bar{z}^2}$ but not necessarily intertwining the operators Mz and
$M_{\bar{z}^2}$ but not necessarily intertwining the operators Mz and  $M_{\bar{z}}$ has been identified.
$M_{\bar{z}}$ has been identified.• As a consequence of our main results, we investigate the properties of the above classes of conjugations keeping the whole Hardy space, model space and Beurling-type subspaces invariant.
• At the end, we extend our discussions in connection to MB, where B is a finite Blaschke product.
The paper is organized as follows: In ![]() $\S$ 2, we characterize the commutant of the multiplication operator MB in
$\S$ 2, we characterize the commutant of the multiplication operator MB in ![]() $L^2(\mathbb{T})$ for any finite Blaschke product B. Some new conjugations in
$L^2(\mathbb{T})$ for any finite Blaschke product B. Some new conjugations in ![]() $L^2(\mathbb{T})$ have been introduced as a generalization of some well-known conjugations, in
$L^2(\mathbb{T})$ have been introduced as a generalization of some well-known conjugations, in ![]() $\S$ 3. Next, we provide the answer to Question 1 and Question 2 in
$\S$ 3. Next, we provide the answer to Question 1 and Question 2 in ![]() $\S$ 4. In
$\S$ 4. In ![]() $\S$ 5, we discuss the properties of such conjugations that keep invariant the entire Hardy space, model space and Beurling-type subspaces. Section 6 is devoted to studying the related results in the case of finite Blaschke product B and, in particular, for
$\S$ 5, we discuss the properties of such conjugations that keep invariant the entire Hardy space, model space and Beurling-type subspaces. Section 6 is devoted to studying the related results in the case of finite Blaschke product B and, in particular, for ![]() $B(z)=z^n$.
$B(z)=z^n$.
2. Commutant of MB in  $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
In this section, we provide a characterization of commutants of the multiplication operator MB having symbol B, where B is a finite Blaschke product. It is worth mentioning that, in [Reference Abkar, Cao and Zhu1, Reference Cowen and Wahl5, Reference Gallardo-Gutiérrez and Partington16], the authors obtained the commutant of MB in various reproducing kernel Hilbert spaces of analytic functions. In contrast with the existing results, we obtain the commutant of MB { in ![]() $L^2(\mathbb{T})$, and our characterization result is different from the existing ones. We denote
$L^2(\mathbb{T})$, and our characterization result is different from the existing ones. We denote ![]() $\{M_B\}^\prime$ to be the set of all bounded linear operators on
$\{M_B\}^\prime$ to be the set of all bounded linear operators on ![]() $L^2(\mathbb{T})$ that commutes with MB. In other words, if
$L^2(\mathbb{T})$ that commutes with MB. In other words, if ![]() $T\in \{M_B\}^\prime$, then
$T\in \{M_B\}^\prime$, then ![]() $T:L^2(\mathbb{T})\to L^2(\mathbb{T})$ is a bounded linear operator such that
$T:L^2(\mathbb{T})\to L^2(\mathbb{T})$ is a bounded linear operator such that ![]() $TM_B=M_BT$. Our main aim is to characterize the set
$TM_B=M_BT$. Our main aim is to characterize the set ![]() $\{M_B\}^\prime$, and to achieve our goal; we need the following useful lemma.
$\{M_B\}^\prime$, and to achieve our goal; we need the following useful lemma.
Lemma 2.1. Let ![]() $\phi \in L^2(\mathbb{T})$ be such that
$\phi \in L^2(\mathbb{T})$ be such that ![]() $\phi f \in L^2(\mathbb{T})$ for all
$\phi f \in L^2(\mathbb{T})$ for all ![]() $f\in L^2(\mathbb{T})$, then
$f\in L^2(\mathbb{T})$, then ![]() $\phi \in L^\infty (\mathbb{T})$.
$\phi \in L^\infty (\mathbb{T})$.
Proof. By the Closed-Graph theorem, we can show that the multiplication operator Mϕ on ![]() $L^2(\mathbb{T})$, defined by:
$L^2(\mathbb{T})$, defined by:
is a well-defined bounded linear operator. Then using similar argument as in [Reference Partington31, Theorem 1.6.2], one can show that ![]() $\phi \in L^\infty (\mathbb{T})$.
$\phi \in L^\infty (\mathbb{T})$.
Before going to the main theorem in this section, we need to recall some basic facts. For any inner function θ, by Wold-type Decomposition [Reference Sz.-Nagy, Foias, Bercovici and Kérchy36], we can view ![]() $L^2(\mathbb{T})$ as follows:
$L^2(\mathbb{T})$ as follows:
 \begin{equation}
L^2(\mathbb{T}) =\bigoplus _{k=-\infty}^{\infty}\theta ^k K_\theta.
\end{equation}
\begin{equation}
L^2(\mathbb{T}) =\bigoplus _{k=-\infty}^{\infty}\theta ^k K_\theta.
\end{equation} The proof of the above decomposition (2.1) is easily obtained from the fact that the corresponding Toeplitz operator Tθ is a pure isometry and using the decomposition  $L^2(\mathbb{T})=H^2 \oplus \overline{H^2_0}$. For reader convenience, we briefly discuss the proof of the above decomposition. Applying the classical Von Neumann-Wold Decomposition theorem on H 2 associated with the shift operator Tθ we obtain the following:
$L^2(\mathbb{T})=H^2 \oplus \overline{H^2_0}$. For reader convenience, we briefly discuss the proof of the above decomposition. Applying the classical Von Neumann-Wold Decomposition theorem on H 2 associated with the shift operator Tθ we obtain the following:  $H^2 (\mathbb{T}) =\bigoplus\limits _{k=0}^{\infty}\theta ^k K_\theta .$ Therefore, for any
$H^2 (\mathbb{T}) =\bigoplus\limits _{k=0}^{\infty}\theta ^k K_\theta .$ Therefore, for any ![]() $h\in H^2(\mathbb{T})$, there exists a sequence
$h\in H^2(\mathbb{T})$, there exists a sequence ![]() $\{h_k\}_{k=0}^\infty$ in Kθ such that
$\{h_k\}_{k=0}^\infty$ in Kθ such that  $h=\sum\limits_{k=0}^{\infty}h_k\theta^k$ and
$h=\sum\limits_{k=0}^{\infty}h_k\theta^k$ and  $\|h\lVert^2=\sum\limits_{k=0}^{\infty}\|h_k\lVert^2$. Note that,
$\|h\lVert^2=\sum\limits_{k=0}^{\infty}\|h_k\lVert^2$. Note that, ![]() $\theta^k K_\theta \perp \theta^m K_\theta$ for any
$\theta^k K_\theta \perp \theta^m K_\theta$ for any ![]() $k\neq m\in \mathbb{Z}$. As a consequence, we have
$k\neq m\in \mathbb{Z}$. As a consequence, we have  $\bigoplus\limits _{k=-\infty}^{\infty}\theta ^k K_\theta \subseteq L^2(\mathbb{T}).$ Let
$\bigoplus\limits _{k=-\infty}^{\infty}\theta ^k K_\theta \subseteq L^2(\mathbb{T}).$ Let  $f\in L^2(\mathbb{T})=H^2\oplus \overline{H^2_0}$, then there exist
$f\in L^2(\mathbb{T})=H^2\oplus \overline{H^2_0}$, then there exist ![]() $f_1\in H^2$ and
$f_1\in H^2$ and  $f_2 \in \overline{H^2_0}$ such that
$f_2 \in \overline{H^2_0}$ such that ![]() $f=f_1\oplus f_2$. Again,
$f=f_1\oplus f_2$. Again,  $f_1=\sum\limits_{k=0}^{\infty}\tilde{f}_k\theta^k$, where
$f_1=\sum\limits_{k=0}^{\infty}\tilde{f}_k\theta^k$, where  $\{\tilde{f}_k\}_{k=0}^\infty \in K_\theta$ and
$\{\tilde{f}_k\}_{k=0}^\infty \in K_\theta$ and ![]() $f_2=\overline{zg}$ for some
$f_2=\overline{zg}$ for some ![]() $g\in H^2$. Moreover, we have
$g\in H^2$. Moreover, we have  $g=\sum\limits_{k=0}^{\infty}g_k\theta^k$, where
$g=\sum\limits_{k=0}^{\infty}g_k\theta^k$, where ![]() $\{g_k\}_{k=0}^\infty \in K_\theta$ and hence,
$\{g_k\}_{k=0}^\infty \in K_\theta$ and hence,
 \begin{align*}
f_2 = \sum_{k=0}^{\infty}\overline{zg_k}{\theta}^{-k} =\sum_{k=0}^{\infty}\overline{zg_k}\theta \theta^{-(k+1)}=\sum_{k=0}^{\infty}(c_\theta g_k)\theta^{-(k+1)}
&= \sum_{k=-\infty}^{-1}\tilde{g}_k\theta^k,
\end{align*}
\begin{align*}
f_2 = \sum_{k=0}^{\infty}\overline{zg_k}{\theta}^{-k} =\sum_{k=0}^{\infty}\overline{zg_k}\theta \theta^{-(k+1)}=\sum_{k=0}^{\infty}(c_\theta g_k)\theta^{-(k+1)}
&= \sum_{k=-\infty}^{-1}\tilde{g}_k\theta^k,
\end{align*} where ![]() $\tilde{g}_k=c_\theta g_k \in K_\theta $. Finally, combining all the above facts, we conclude,
$\tilde{g}_k=c_\theta g_k \in K_\theta $. Finally, combining all the above facts, we conclude,  $f=\sum\limits_{k=-\infty}^{\infty}f_k\theta^k,$ where
$f=\sum\limits_{k=-\infty}^{\infty}f_k\theta^k,$ where ![]() $f_k= \tilde{f}_k$ for
$f_k= \tilde{f}_k$ for ![]() $k\geq 0$ and
$k\geq 0$ and ![]() $f_k= \tilde{g}_k$ for k < 0.
$f_k= \tilde{g}_k$ for k < 0.
We know that for a finite Blaschke product B, the dimension of the model space ![]() $K_B:= H^2\ominus BH^2$ is finite. In fact, if the degree of B is a finite natural number n, then
$K_B:= H^2\ominus BH^2$ is finite. In fact, if the degree of B is a finite natural number n, then ![]() $dim(K_B)=n$. Let
$dim(K_B)=n$. Let ![]() $\{h_1,h_2,\ldots,h_n \}$ be an orthonormal basis of KB. Now, due to Wold-type decomposition as discussed above, the space
$\{h_1,h_2,\ldots,h_n \}$ be an orthonormal basis of KB. Now, due to Wold-type decomposition as discussed above, the space ![]() $L^2(\mathbb{T})$ can be viewed as follows:
$L^2(\mathbb{T})$ can be viewed as follows:
 \begin{equation*}
L^2(\mathbb{T})= \bigoplus_{k=-\infty}^{\infty}B^k K_B.
\end{equation*}
\begin{equation*}
L^2(\mathbb{T})= \bigoplus_{k=-\infty}^{\infty}B^k K_B.
\end{equation*} Using the above decomposition we identify ![]() $L^2(\mathbb{T})$ as orthogonal direct sum of n-closed subspaces, that is:
$L^2(\mathbb{T})$ as orthogonal direct sum of n-closed subspaces, that is:
where
 \begin{equation*}
\mathcal{H}_1(h_1,B):=\bigvee_{k=-\infty}^\infty \{h_1 B^k\}, ~\mathcal{H}_2(h_2,B):=\bigvee_{k=-\infty}^\infty \{h_2 B^k\},\ldots ,\mathcal{H}_n(h_n,B):=\bigvee_{k=-\infty}^\infty \{h_nB^k\}.
\end{equation*}
\begin{equation*}
\mathcal{H}_1(h_1,B):=\bigvee_{k=-\infty}^\infty \{h_1 B^k\}, ~\mathcal{H}_2(h_2,B):=\bigvee_{k=-\infty}^\infty \{h_2 B^k\},\ldots ,\mathcal{H}_n(h_n,B):=\bigvee_{k=-\infty}^\infty \{h_nB^k\}.
\end{equation*} Therefore, for any ![]() $f\in L^2(\mathbb{T}) $ can be represented as
$f\in L^2(\mathbb{T}) $ can be represented as ![]() $f=f_1+f_2+ \cdots +f_n$, where
$f=f_1+f_2+ \cdots +f_n$, where ![]() $f_i \in \mathcal{H}_i(h_i,B)$ for
$f_i \in \mathcal{H}_i(h_i,B)$ for ![]() $i\in \{1,2,\ldots ,n\}$. For a finite sequence
$i\in \{1,2,\ldots ,n\}$. For a finite sequence ![]() $\{\lambda_k \}_{1\leq k \leq n}$ (maybe repeating) in
$\{\lambda_k \}_{1\leq k \leq n}$ (maybe repeating) in ![]() $\mathbb{D}$, we consider the following finite Blaschke product:
$\mathbb{D}$, we consider the following finite Blaschke product:
 \begin{equation}
B(z)=\prod_{k=1}^n\dfrac{\lambda_k -z}{1-\bar{\lambda}_k z},quad z\in \overline{\mathbb{D}}.
\end{equation}
\begin{equation}
B(z)=\prod_{k=1}^n\dfrac{\lambda_k -z}{1-\bar{\lambda}_k z},quad z\in \overline{\mathbb{D}}.
\end{equation} For ![]() $1\leq j\leq n$, consider the following functions:
$1\leq j\leq n$, consider the following functions:
 \begin{align}
e_j(z) = &\Big(\prod_{k=1}^{j-1}\dfrac{\lambda_k -z}{1-\bar{\lambda}_k z}\Big)\dfrac{\sqrt{1-|\lambda_j|^2}}{1-\bar{\lambda}_j z},
\end{align}
\begin{align}
e_j(z) = &\Big(\prod_{k=1}^{j-1}\dfrac{\lambda_k -z}{1-\bar{\lambda}_k z}\Big)\dfrac{\sqrt{1-|\lambda_j|^2}}{1-\bar{\lambda}_j z},
\end{align} then it is easy to observe that ![]() $\{e_1,e_2,\ldots ,e_n \}$ forms an orthonormal basis of KB. In fact, this is a standard orthonormal basis of KB, and for more details, we refer to [[Reference Fricain and Mashreghi14], Theorem: 14.7]. It is worth mentioning some nice properties of ej as follows:
$\{e_1,e_2,\ldots ,e_n \}$ forms an orthonormal basis of KB. In fact, this is a standard orthonormal basis of KB, and for more details, we refer to [[Reference Fricain and Mashreghi14], Theorem: 14.7]. It is worth mentioning some nice properties of ej as follows:
(i)
 $e_j \in H^\infty (\mathbb{T})$ for
$e_j \in H^\infty (\mathbb{T})$ for  $1\leq j\leq n$.
$1\leq j\leq n$.(ii) For
 $1\leq j\leq n$, each ej is invertible in
$1\leq j\leq n$, each ej is invertible in  $L^\infty (\mathbb{T})$, and
$L^\infty (\mathbb{T})$, and
 \begin{equation*}
e_j ^{-1}(z)=\Big(\prod_{k=1}^{j-1}\dfrac{1-\bar{\lambda}_k z}{\lambda_k -z}\Big)\dfrac{1-\bar{\lambda}_j z}{\sqrt{1-|\lambda_j|^2}}.
\end{equation*}
\begin{equation*}
e_j ^{-1}(z)=\Big(\prod_{k=1}^{j-1}\dfrac{1-\bar{\lambda}_k z}{\lambda_k -z}\Big)\dfrac{1-\bar{\lambda}_j z}{\sqrt{1-|\lambda_j|^2}}.
\end{equation*}
Now, we proceed to find the commutant of MB. To this end, we use the decomposition of ![]() $L^2(\mathbb{T})$ as an orthogonal direct sum of n-subspaces given in (2.2), along with the fact that B is of the form (2.3) and
$L^2(\mathbb{T})$ as an orthogonal direct sum of n-subspaces given in (2.2), along with the fact that B is of the form (2.3) and ![]() $\{e_1,e_2,\ldots ,e_n \}$ is the required orthonormal basis as mentioned in (2.4). Therefore, for any
$\{e_1,e_2,\ldots ,e_n \}$ is the required orthonormal basis as mentioned in (2.4). Therefore, for any ![]() $f\in L^2(\mathbb{T}) \big(= \mathcal{H}_1 (e_1,B) \oplus \mathcal{H}_2(e_2,B) \oplus \cdots \oplus \mathcal{H}_n(e_n,B)\big)$ can be written as
$f\in L^2(\mathbb{T}) \big(= \mathcal{H}_1 (e_1,B) \oplus \mathcal{H}_2(e_2,B) \oplus \cdots \oplus \mathcal{H}_n(e_n,B)\big)$ can be written as ![]() $f=f_1\oplus f_2\oplus\cdots \oplus f_n$, where
$f=f_1\oplus f_2\oplus\cdots \oplus f_n$, where ![]() $f_i \in \mathcal{H}_i(e_i,B) $ for each
$f_i \in \mathcal{H}_i(e_i,B) $ for each ![]() $i\in \{1,2,\ldots ,n \}$. Let
$i\in \{1,2,\ldots ,n \}$. Let ![]() $S\in \{M_B \}^\prime$, then S is a bounded linear operator on
$S\in \{M_B \}^\prime$, then S is a bounded linear operator on ![]() $L^2(\mathbb{T})$ such that
$L^2(\mathbb{T})$ such that ![]() $M_BS=SM_B$. Since
$M_BS=SM_B$. Since ![]() $f_j\in \mathcal{H}_j(e_j,B) $, then there exists
$f_j\in \mathcal{H}_j(e_j,B) $, then there exists  $g_j=\sum\limits_{k=-\infty}^{\infty}a^j_kB^k \in L^2(\mathbb{T})$ such that
$g_j=\sum\limits_{k=-\infty}^{\infty}a^j_kB^k \in L^2(\mathbb{T})$ such that ![]() $f_j=e_jg_j$ for
$f_j=e_jg_j$ for ![]() $j\in \{1,2, \ldots ,n \}$. Since
$j\in \{1,2, \ldots ,n \}$. Since  $e_j^{-1}\in L^\infty(\mathbb{T})$, then by using the fact that S commutes with MB we have:
$e_j^{-1}\in L^\infty(\mathbb{T})$, then by using the fact that S commutes with MB we have:
 \begin{align*}
Sf_j &= (Se_j)g_j
=(Se_j)e_j^{-1}e_j g_j
=(Se_j)e_j^{-1}f_j=\phi_jf_j,
\end{align*}
\begin{align*}
Sf_j &= (Se_j)g_j
=(Se_j)e_j^{-1}e_j g_j
=(Se_j)e_j^{-1}f_j=\phi_jf_j,
\end{align*} where  $\phi_j = (Se_j)e_j^{-1} \in L^2(\mathbb{T})$. Next we claim that
$\phi_j = (Se_j)e_j^{-1} \in L^2(\mathbb{T})$. Next we claim that ![]() $\phi_j \in L^\infty (\mathbb{T})$ for
$\phi_j \in L^\infty (\mathbb{T})$ for ![]() $j\in \{1,2,\ldots ,n\}$. We already proved that
$j\in \{1,2,\ldots ,n\}$. We already proved that ![]() $\phi_jf_j =Sf_j\in L^2(\mathbb{T})$. Now for i ≠ j,
$\phi_jf_j =Sf_j\in L^2(\mathbb{T})$. Now for i ≠ j,
 \begin{align*}
\phi_jf_i & = \phi_j(e_ig_i)=e_j^{-1}e_j \phi_j(e_ig_i)=e_j^{-1}e_i(\phi_je_jg_i)=e_j^{-1}e_i S(h_j) \in L^2(\mathbb{T}),
\end{align*}
\begin{align*}
\phi_jf_i & = \phi_j(e_ig_i)=e_j^{-1}e_j \phi_j(e_ig_i)=e_j^{-1}e_i(\phi_je_jg_i)=e_j^{-1}e_i S(h_j) \in L^2(\mathbb{T}),
\end{align*} where ![]() $h_j= e_jg_i \in \mathcal{H}_j(e_j,B)$. Thus, we have
$h_j= e_jg_i \in \mathcal{H}_j(e_j,B)$. Thus, we have ![]() $\phi_jf=\phi_j f_1+\phi_jf_2+\cdots +\phi_jf_n\in L^2(\mathbb{T})$ for any
$\phi_jf=\phi_j f_1+\phi_jf_2+\cdots +\phi_jf_n\in L^2(\mathbb{T})$ for any ![]() $f\in L^2(\mathbb{T})$. Therefore by using Lemma 2.1 we conclude
$f\in L^2(\mathbb{T})$. Therefore by using Lemma 2.1 we conclude ![]() $\phi_j \in L^\infty(\mathbb{T})$ for
$\phi_j \in L^\infty(\mathbb{T})$ for ![]() $j\in \{1,2,\ldots ,n\}$. Since each
$j\in \{1,2,\ldots ,n\}$. Since each ![]() $\phi_j\in L^\infty(\mathbb{T})$, then for
$\phi_j\in L^\infty(\mathbb{T})$, then for ![]() $f\in L^2(\mathbb{T})$ the action of S is given as follows:
$f\in L^2(\mathbb{T})$ the action of S is given as follows:
 \begin{align*}
Sf = & \phi_1f_1 + \phi_2f_2 + \cdots +\phi_nf_n \\
= & M_{\phi_1}f_1 + M_{\phi_2}f_2 + \cdots + M_{\phi_n}f_n.
\end{align*}
\begin{align*}
Sf = & \phi_1f_1 + \phi_2f_2 + \cdots +\phi_nf_n \\
= & M_{\phi_1}f_1 + M_{\phi_2}f_2 + \cdots + M_{\phi_n}f_n.
\end{align*} From now onward, we use the notation ![]() $M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ to denote the bounded linear operator on
$M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ to denote the bounded linear operator on ![]() $L^2(\mathbb{T})$ such that:
$L^2(\mathbb{T})$ such that:
Summing up, we have the following main theorem in this section, and it is extremely useful in later sections to prove other characterization results. Moreover, we expect that the following theorem will have an independent interest in the future.
Theorem 2.2. Let B be a finite Blaschke product of degree n and ![]() $S\in \{M_B\}^\prime$ in
$S\in \{M_B\}^\prime$ in ![]() $L^2(\mathbb{T})$. Then there exist n-number of
$L^2(\mathbb{T})$. Then there exist n-number of ![]() $L^\infty(\mathbb{T})$ functions
$L^\infty(\mathbb{T})$ functions ![]() $\phi_1,\phi_2,\ldots ,\phi_n$ such that
$\phi_1,\phi_2,\ldots ,\phi_n$ such that ![]() $S=M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$.
$S=M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$.
One can find the classical theorem for the commutant of the shift operator on ![]() $L^2(\mathbb{T})$-space in [Reference Martínez-Avendaño and Rosenthal28](see Theorem: 2.2.5), which says that the commutant of Mz in
$L^2(\mathbb{T})$-space in [Reference Martínez-Avendaño and Rosenthal28](see Theorem: 2.2.5), which says that the commutant of Mz in ![]() $L^2(\mathbb{T})$ is
$L^2(\mathbb{T})$ is ![]() $\{M_\phi:\phi \in L^\infty(\mathbb{T})\}$. It is worth noticing that, if we consider
$\{M_\phi:\phi \in L^\infty(\mathbb{T})\}$. It is worth noticing that, if we consider ![]() $\phi_1=\phi_2=\cdots =\phi_n=\phi$ in (2.5), then
$\phi_1=\phi_2=\cdots =\phi_n=\phi$ in (2.5), then ![]() $M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ turns out to be the classical multiplication operator Mϕ. Therefore we have the following remark:
$M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ turns out to be the classical multiplication operator Mϕ. Therefore we have the following remark:
Remark 2.3. Suppose ![]() $B(z)=z^n$ and
$B(z)=z^n$ and ![]() $S\in \{M_{z^n}\}^\prime$. Since
$S\in \{M_{z^n}\}^\prime$. Since ![]() $\{M_z\}^\prime \subset \{M_{z^n}\}^\prime$, then
$\{M_z\}^\prime \subset \{M_{z^n}\}^\prime$, then
(i) for
 $S\in \{M_z\}^\prime$, there exists
$S\in \{M_z\}^\prime$, there exists  $\phi \in L^\infty$ such that
$\phi \in L^\infty$ such that  $S=M_{[\phi,\phi,\dots,\phi]}=M_{\phi}$,
$S=M_{[\phi,\phi,\dots,\phi]}=M_{\phi}$,(ii) for
 $S\notin \{M_z\}^\prime$, there exist
$S\notin \{M_z\}^\prime$, there exist  $\phi_1,\phi_2,\ldots ,\phi_n \in L^\infty$ with
$\phi_1,\phi_2,\ldots ,\phi_n \in L^\infty$ with  $\phi_i\neq\phi_j$ for some
$\phi_i\neq\phi_j$ for some  $i,j\in \{1,2, \ldots ,n\}$ such that
$i,j\in \{1,2, \ldots ,n\}$ such that  $S=M_{[\phi_1,\phi_2 , \ldots ,\phi_n]}$.
$S=M_{[\phi_1,\phi_2 , \ldots ,\phi_n]}$.
In a similar fashion, one can distinguish between the commutant of Mz and the commutant of MB, where B is a finite Blaschke product.
3. Conjugations in  $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
We begin the section by recalling two natural conjugations in ![]() $L^2(\mathbb{T})$ which have been mentioned earlier, namely J and
$L^2(\mathbb{T})$ which have been mentioned earlier, namely J and ![]() $J^\star$, where J is defined by
$J^\star$, where J is defined by ![]() $Jf=\bar{f}$ and
$Jf=\bar{f}$ and ![]() $J^\star$ is given by
$J^\star$ is given by ![]() $J^\star f= f^\sharp$, where
$J^\star f= f^\sharp$, where ![]() $f^\sharp(z)=\overline{f(\bar{z})}$. These two conjugations have some interesting properties. The bilateral shift Mz becomes complex symmetric in
$f^\sharp(z)=\overline{f(\bar{z})}$. These two conjugations have some interesting properties. The bilateral shift Mz becomes complex symmetric in ![]() $L^2(\mathbb{T})$ with respect to the conjugation J, and it maps the analytic functions space
$L^2(\mathbb{T})$ with respect to the conjugation J, and it maps the analytic functions space ![]() $H^2(\mathbb{T})$ into the co-analytic functions space
$H^2(\mathbb{T})$ into the co-analytic functions space ![]() $\overline{H^2}(\mathbb{T})$, that is,
$\overline{H^2}(\mathbb{T})$, that is, ![]() $J(H^2(\mathbb{T}))=\overline{H^2}(\mathbb{T})$. On the other hand, the conjugation
$J(H^2(\mathbb{T}))=\overline{H^2}(\mathbb{T})$. On the other hand, the conjugation ![]() $J^\star$ commutes with Mz and keeps the analytic function space
$J^\star$ commutes with Mz and keeps the analytic function space ![]() $H^2(\mathbb{T})$ invariant, that is,
$H^2(\mathbb{T})$ invariant, that is, ![]() $J^\star (H^2(\mathbb{T}))\subset H^2(\mathbb{T})$. As discussed earlier, we will introduce some conjugations in
$J^\star (H^2(\mathbb{T}))\subset H^2(\mathbb{T})$. As discussed earlier, we will introduce some conjugations in ![]() $L^2(\mathbb{T})$ as a generalization of these two conjugations J and
$L^2(\mathbb{T})$ as a generalization of these two conjugations J and ![]() $J^\star$ from a different point of view. Going further, for any inner function θ, the natural conjugation on
$J^\star$ from a different point of view. Going further, for any inner function θ, the natural conjugation on ![]() $K_\theta := H^2\ominus \theta H^2$ is given by:
$K_\theta := H^2\ominus \theta H^2$ is given by:
 \begin{align*}
c_\theta:& K_{\theta} \to K_{\theta}\\
& h\mapsto \overline{zh}\theta,
\end{align*}
\begin{align*}
c_\theta:& K_{\theta} \to K_{\theta}\\
& h\mapsto \overline{zh}\theta,
\end{align*}and it has a connection with the truncated Toeplitz operator in model spaces. For example, the truncated Toeplitz operator is cθ-symmetric (for more details, see [Reference Garcia, Mashreghi and Ross17, Reference Garcia and Putinar19]).
For any inner function θ, by Wold-type Decomposition (2.1) in ![]() $\S$ 2, we define conjugations extending the natural conjugation cθ from the model space Kθ to the entire
$\S$ 2, we define conjugations extending the natural conjugation cθ from the model space Kθ to the entire ![]() $L^2(\mathbb{T})$ space in two different ways. First, we define
$L^2(\mathbb{T})$ space in two different ways. First, we define ![]() $\mathscr{C}_\theta$ on
$\mathscr{C}_\theta$ on ![]() $L^2(\mathbb{T})$ as follows:
$L^2(\mathbb{T})$ as follows:
 \begin{align*}
\mathscr{C}_\theta: & L^2(\mathbb{T}) \to L^2(\mathbb{T})\\
& f \mapsto \sum_{k=-\infty}^{\infty}(c_\theta f_k) \theta ^{-k}, \quad \text{where}~ f=\sum_{k=-\infty}^{\infty}f_k\theta ^{k} ,f_k \in K_\theta, ~\text{that is}:
\end{align*}
\begin{align*}
\mathscr{C}_\theta: & L^2(\mathbb{T}) \to L^2(\mathbb{T})\\
& f \mapsto \sum_{k=-\infty}^{\infty}(c_\theta f_k) \theta ^{-k}, \quad \text{where}~ f=\sum_{k=-\infty}^{\infty}f_k\theta ^{k} ,f_k \in K_\theta, ~\text{that is}:
\end{align*} \begin{equation} \mathscr{C}_\theta(\sum_{k=-\infty}^{\infty}f_k\theta ^k )= \sum_{k=-\infty}^{\infty}\overline{zf_k}\theta ^{-k+1}.
\end{equation}
\begin{equation} \mathscr{C}_\theta(\sum_{k=-\infty}^{\infty}f_k\theta ^k )= \sum_{k=-\infty}^{\infty}\overline{zf_k}\theta ^{-k+1}.
\end{equation} It is easy to check that ![]() $\mathscr{C}_\theta$ is a conjugation on
$\mathscr{C}_\theta$ is a conjugation on ![]() $L^2(\mathbb{T})$. In particular, if
$L^2(\mathbb{T})$. In particular, if ![]() $\theta (z)=z$, then the action of
$\theta (z)=z$, then the action of ![]() $\mathscr{C}_z$ is given by:
$\mathscr{C}_z$ is given by:
 \begin{equation}
\mathscr{C}_z(\sum_{k=-\infty}^{\infty}a_kz^k)=\sum_{k=-\infty}^{\infty}\bar{a}_k\bar{z}^k.
\end{equation}
\begin{equation}
\mathscr{C}_z(\sum_{k=-\infty}^{\infty}a_kz^k)=\sum_{k=-\infty}^{\infty}\bar{a}_k\bar{z}^k.
\end{equation} Note that the action of ![]() $\mathscr{C}_\theta$ given in (3.1) can also be rewritten as:
$\mathscr{C}_\theta$ given in (3.1) can also be rewritten as:
and hence ![]() $\mathscr{C}_z(f)=\bar{f}$. In other words,
$\mathscr{C}_z(f)=\bar{f}$. In other words, ![]() $\mathscr{C}_z=J$, and we can think
$\mathscr{C}_z=J$, and we can think ![]() $\mathscr{C}_\theta $ is a generalization of the conjugation J. These types of conjugations (3.3) have already been introduced in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10], where they use it to characterize all Mz-commuting and Mz,
$\mathscr{C}_\theta $ is a generalization of the conjugation J. These types of conjugations (3.3) have already been introduced in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10], where they use it to characterize all Mz-commuting and Mz, ![]() $M_{\bar{z}}$-intertwining conjugations preserving model spaces.
$M_{\bar{z}}$-intertwining conjugations preserving model spaces.
Now we define another conjugation (different from ![]() $\mathscr{C}_\theta$ above) corresponding to an inner function θ, namely
$\mathscr{C}_\theta$ above) corresponding to an inner function θ, namely ![]() $\mathscr{C}_\theta ^\star :L^2(\mathbb{T})\to L^2(\mathbb{T})$ such that if
$\mathscr{C}_\theta ^\star :L^2(\mathbb{T})\to L^2(\mathbb{T})$ such that if  $f=\sum\limits_{k=-\infty}^{\infty}f_k\theta ^{k}$ with
$f=\sum\limits_{k=-\infty}^{\infty}f_k\theta ^{k}$ with ![]() $f_k \in K_\theta$, then
$f_k \in K_\theta$, then  $\mathscr{C}_\theta^\star(f)=\sum\limits_{k=-\infty}^{\infty}(c_\theta f_k) \theta ^{k},$ which implies that:
$\mathscr{C}_\theta^\star(f)=\sum\limits_{k=-\infty}^{\infty}(c_\theta f_k) \theta ^{k},$ which implies that:
 \begin{equation}
\mathscr{C}_\theta^\star(\sum_{k=-\infty}^{\infty}f_k\theta ^k )= \sum_{k=-\infty}^{\infty}\overline{zf_k}\theta ^{k-1}.
\end{equation}
\begin{equation}
\mathscr{C}_\theta^\star(\sum_{k=-\infty}^{\infty}f_k\theta ^k )= \sum_{k=-\infty}^{\infty}\overline{zf_k}\theta ^{k-1}.
\end{equation} In particular, for ![]() $\theta(z)=z$, we have
$\theta(z)=z$, we have ![]() $\mathscr{C}_z ^\star=J^\star$. These types of conjugations can also be found in [Reference Chattopadhyay, Das, Pradhan and Sarkar3].
$\mathscr{C}_z ^\star=J^\star$. These types of conjugations can also be found in [Reference Chattopadhyay, Das, Pradhan and Sarkar3].
In the beginning, we have already discussed certain properties of two natural conjugations J and ![]() $J^\star$. It is easy to observe that those properties also hold for
$J^\star$. It is easy to observe that those properties also hold for ![]() $\mathscr{C}_\theta$ and
$\mathscr{C}_\theta$ and ![]() $\mathscr{C}_\theta ^\star$. To be more specific,
$\mathscr{C}_\theta ^\star$. To be more specific, ![]() $\mathscr{C}_\theta M_\theta =M_{\bar{\theta}}\mathscr{C}_\theta $,
$\mathscr{C}_\theta M_\theta =M_{\bar{\theta}}\mathscr{C}_\theta $, ![]() $\mathscr{C}_\theta (H^2)=\overline{H^2}$,
$\mathscr{C}_\theta (H^2)=\overline{H^2}$, ![]() $\mathscr{C}_\theta^\star M_\theta =M_\theta \mathscr{C}_\theta^\star$, and
$\mathscr{C}_\theta^\star M_\theta =M_\theta \mathscr{C}_\theta^\star$, and ![]() $\mathscr{C}_\theta^\star (H^2)=H^2$. Moreover, the conjugation
$\mathscr{C}_\theta^\star (H^2)=H^2$. Moreover, the conjugation ![]() $\mathscr{C}_{z^2}^\star$ has one more extra property, namely
$\mathscr{C}_{z^2}^\star$ has one more extra property, namely ![]() $\mathscr{C}_{z^2}^\star M_z \neq M_z \mathscr{C}_{z^2}^\star$ and, in general,
$\mathscr{C}_{z^2}^\star M_z \neq M_z \mathscr{C}_{z^2}^\star$ and, in general, ![]() $\mathscr{C}_\theta^\star M_z \neq M_z \mathscr{C}_\theta^\star$ for an inner function θ.
$\mathscr{C}_\theta^\star M_z \neq M_z \mathscr{C}_\theta^\star$ for an inner function θ.
4. Conjugations intertwining  $M_{z^2}$,
$M_{z^2}$,  $M_{\bar{z}^2}$ and commuting with
$M_{\bar{z}^2}$ and commuting with  $M_{z^2}$ In L 2
$M_{z^2}$ In L 2
The definition of the conjugations J, ![]() $J^\star$ in L 2 (see (1.1)) and some of their properties have already been introduced in
$J^\star$ in L 2 (see (1.1)) and some of their properties have already been introduced in ![]() $\S$ 1. In [Reference Câmara, Kliś-Garlicka and Ptak9, Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10], the authors obtained the characterization of all conjugations C intertwining the operators Mz,
$\S$ 1. In [Reference Câmara, Kliś-Garlicka and Ptak9, Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10], the authors obtained the characterization of all conjugations C intertwining the operators Mz, ![]() $M_{\bar{z}}$ in terms J in L 2 (see [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10, Theorem 2.2]). Moreover, they also characterized all conjugations C that commute with the operator Mz in terms of
$M_{\bar{z}}$ in terms J in L 2 (see [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10, Theorem 2.2]). Moreover, they also characterized all conjugations C that commute with the operator Mz in terms of ![]() $J^\star$ in L 2 (see [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10, Theorem 2.4]). Motivated by the characterization results mentioned above, we raise Question 1 and Question 2 in
$J^\star$ in L 2 (see [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10, Theorem 2.4]). Motivated by the characterization results mentioned above, we raise Question 1 and Question 2 in ![]() $\S$ 1. Our main aim in this section is to provide appropriate answers of these questions. First, we characterize all conjugations C that satisfies the identity
$\S$ 1. Our main aim in this section is to provide appropriate answers of these questions. First, we characterize all conjugations C that satisfies the identity ![]() $CM_{z^2}=M_{\bar{z}^2}C$. One of the importance of our Theorem 4.1 below is that the class of conjugations C intertwining the operators
$CM_{z^2}=M_{\bar{z}^2}C$. One of the importance of our Theorem 4.1 below is that the class of conjugations C intertwining the operators ![]() $M_{z^2}$,
$M_{z^2}$, ![]() $M_{\bar{z}^2}$ in L 2 is bigger than the class of conjugations C intertwining the operators Mz,
$M_{\bar{z}^2}$ in L 2 is bigger than the class of conjugations C intertwining the operators Mz, ![]() $M_{\bar{z}}$ in L 2. Before going to the main theorems, we define:
$M_{\bar{z}}$ in L 2. Before going to the main theorems, we define:
 \begin{equation*}\phi^e(z)=\dfrac{\phi(z)+\phi(-z)}{2} \quad \text{and}\quad \phi^o(z)=\dfrac{\phi(z)-\phi(-z)}{2}, \quad \text{for}\quad\phi \in L^2(\mathbb{T}).\end{equation*}
\begin{equation*}\phi^e(z)=\dfrac{\phi(z)+\phi(-z)}{2} \quad \text{and}\quad \phi^o(z)=\dfrac{\phi(z)-\phi(-z)}{2}, \quad \text{for}\quad\phi \in L^2(\mathbb{T}).\end{equation*} Note that, ![]() $\phi^e \in \bigvee_{k=-\infty}^{\infty}\{z^{2k}\}=\mathcal{H}_1(1,z^2)$ and
$\phi^e \in \bigvee_{k=-\infty}^{\infty}\{z^{2k}\}=\mathcal{H}_1(1,z^2)$ and ![]() $\phi^o \in \bigvee_{k=-\infty}^{\infty}\{z^{2k+1}\}=\mathcal{H}_2(z,z^2)$. Next, we state and prove one of our main results in this section which involve the conjugation
$\phi^o \in \bigvee_{k=-\infty}^{\infty}\{z^{2k+1}\}=\mathcal{H}_2(z,z^2)$. Next, we state and prove one of our main results in this section which involve the conjugation ![]() $\mathscr{C}_{z^2}(f)=z\overline{f}$ for
$\mathscr{C}_{z^2}(f)=z\overline{f}$ for ![]() $f\in L^2$ (see (3.3)).
$f\in L^2$ (see (3.3)).
Theorem 4.1. Let ![]() $C:L^2(\mathbb{T})\to L^2(\mathbb{T})$ be an arbitrary conjugation such that
$C:L^2(\mathbb{T})\to L^2(\mathbb{T})$ be an arbitrary conjugation such that ![]() $CM_{z^2}=M_{\bar{z}^2}C$, then there exist
$CM_{z^2}=M_{\bar{z}^2}C$, then there exist ![]() $\phi_1,\phi_2\in L^\infty$ such that
$\phi_1,\phi_2\in L^\infty$ such that ![]() $C= M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}$, where
$C= M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}$, where ![]() $\phi_1,\phi_2$ satisfies
$\phi_1,\phi_2$ satisfies ![]() $|\phi_1|^2+|\phi_2|^2=2$ and
$|\phi_1|^2+|\phi_2|^2=2$ and ![]() $\phi_1^e= \phi_2^e$. Conversely, any conjugation C of the form
$\phi_1^e= \phi_2^e$. Conversely, any conjugation C of the form ![]() $M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}$ for
$M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}$ for ![]() $\phi_1, \phi_2 \in L^\infty$ satisfies
$\phi_1, \phi_2 \in L^\infty$ satisfies ![]() $CM_{z^2}=M_{\bar{z}^2}C$.
$CM_{z^2}=M_{\bar{z}^2}C$.
Proof. Suppose C is a conjugation on ![]() $L^2(\mathbb{T})$ such that
$L^2(\mathbb{T})$ such that ![]() $CM_{z^2}=M_{\bar{z}^2}C$. Then, it is easy to observe that the unitary operator
$CM_{z^2}=M_{\bar{z}^2}C$. Then, it is easy to observe that the unitary operator ![]() $C\circ\mathscr{C}_{z^2}$ commutes with
$C\circ\mathscr{C}_{z^2}$ commutes with ![]() $M_{z^2}$. Therefore by applying Theorem 2.2, we have:
$M_{z^2}$. Therefore by applying Theorem 2.2, we have:
and hence ![]() $C = M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2} $. By considering the decomposition
$C = M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2} $. By considering the decomposition ![]() $L^2(\mathbb{T})=\mathcal{H}_1(1,z^2) \oplus \mathcal{H}_2(z,z^2)$, we have the following block-matrix representation of
$L^2(\mathbb{T})=\mathcal{H}_1(1,z^2) \oplus \mathcal{H}_2(z,z^2)$, we have the following block-matrix representation of ![]() $M_{[\phi_1,\phi_2]}$:
$M_{[\phi_1,\phi_2]}$:
 \begin{equation*}
M_{[\phi_1,\phi_2]}=
\begin{bmatrix}
M_{\phi_1^e} && M_{\phi_2^o}\\
\\
M_{\phi_1^o} && M_{\phi_2^e}\\
\end{bmatrix} \text{,~and~hence~}
M_{[\phi_1,\phi_2]}^*=
\begin{bmatrix}
M_{\bar{\phi_1^e}} && M_{\bar{\phi_1^o}}\\
\\
M_{\bar{\phi_2^0}} && M_{\bar{\phi_2^e}}\\
\end{bmatrix}.
\end{equation*}
\begin{equation*}
M_{[\phi_1,\phi_2]}=
\begin{bmatrix}
M_{\phi_1^e} && M_{\phi_2^o}\\
\\
M_{\phi_1^o} && M_{\phi_2^e}\\
\end{bmatrix} \text{,~and~hence~}
M_{[\phi_1,\phi_2]}^*=
\begin{bmatrix}
M_{\bar{\phi_1^e}} && M_{\bar{\phi_1^o}}\\
\\
M_{\bar{\phi_2^0}} && M_{\bar{\phi_2^e}}\\
\end{bmatrix}.
\end{equation*} From (4.1) it follows that ![]() $M_{[\phi_1,\phi_2]}$ is a unitary operator, and therefore we obtain the following conditions on the symbols:
$M_{[\phi_1,\phi_2]}$ is a unitary operator, and therefore we obtain the following conditions on the symbols:
 \begin{equation}
\begin{cases}
|\phi_1^e|^2+|\phi_1^o|^2=1 ~,~ |\phi_1^e|^2+|\phi_1^o|^2=1,\\
|\phi_1^e|^2+|\phi_2^o|^2=1 ~,~ |\phi_1^o|^2 + |\phi_2^e|^2=1,\\
\bar{\phi_1^e}\phi_2^o+\bar{\phi_1^o}\phi_2^e=0 ~,~ \bar{\phi_1^o}\phi_1^e+\bar{\phi_2^e}\phi_2^o=0,
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\phi_1^e|^2+|\phi_1^o|^2=1 ~,~ |\phi_1^e|^2+|\phi_1^o|^2=1,\\
|\phi_1^e|^2+|\phi_2^o|^2=1 ~,~ |\phi_1^o|^2 + |\phi_2^e|^2=1,\\
\bar{\phi_1^e}\phi_2^o+\bar{\phi_1^o}\phi_2^e=0 ~,~ \bar{\phi_1^o}\phi_1^e+\bar{\phi_2^e}\phi_2^o=0,
\end{cases}
\end{equation}which by simplifying, reduces to:
 \begin{equation}
\begin{cases}
|\phi_1|^2+|\phi_2|^2=2\\
|\phi_1^o+\phi_2^e|^2+|\phi_1^e+\phi_2^o|^2=2.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\phi_1|^2+|\phi_2|^2=2\\
|\phi_1^o+\phi_2^e|^2+|\phi_1^e+\phi_2^o|^2=2.
\end{cases}
\end{equation}Moreover, due to the involutive property of the conjugation C, we have:
 \begin{equation*}
M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2}M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2} = I\implies \mathscr{C}_{z^2}M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2} = M_{[\phi_1,\phi_2]}^*,
\end{equation*}
\begin{equation*}
M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2}M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2} = I\implies \mathscr{C}_{z^2}M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2} = M_{[\phi_1,\phi_2]}^*,
\end{equation*} which by applying on the basis elements 1 or z yields ![]() $\phi_1^e= \phi_2^e$. Therefore, the conditions in (4.3) merged to
$\phi_1^e= \phi_2^e$. Therefore, the conditions in (4.3) merged to ![]() $|\phi_1|^2+|\phi_2|^2=2$.
$|\phi_1|^2+|\phi_2|^2=2$.
For the converse, suppose ![]() $C=M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}$ for
$C=M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}$ for ![]() $\phi_1, \phi_2 \in L^\infty$. Then for
$\phi_1, \phi_2 \in L^\infty$. Then for ![]() $f\in L^2(\mathbb{T})$, there exist
$f\in L^2(\mathbb{T})$, there exist ![]() $f^e \in \mathcal{H}_1(1,z^2)$ and
$f^e \in \mathcal{H}_1(1,z^2)$ and ![]() $f^o \in \mathcal{H}_2(z,z^2)$ such that
$f^o \in \mathcal{H}_2(z,z^2)$ such that ![]() $f=f^e\oplus f^o$. Since
$f=f^e\oplus f^o$. Since ![]() $\mathscr{C}_{z^2}(f)= z\overline{f}$, then we have:
$\mathscr{C}_{z^2}(f)= z\overline{f}$, then we have:
 \begin{align*}
CM_{z^2}(f)=C(z^2f^e\oplus z^2f^o)= & M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}(z^2f^e\oplus z^2f^o)\\ = & M_{[\phi_1,\phi_2]}(\overline{zf^o}\oplus\overline{zf^e})=\phi_1\overline{zf^o}+\phi_2\overline{zf^e}.
\end{align*}
\begin{align*}
CM_{z^2}(f)=C(z^2f^e\oplus z^2f^o)= & M_{[\phi_1,\phi_2]}\mathscr{C}_{z^2}(z^2f^e\oplus z^2f^o)\\ = & M_{[\phi_1,\phi_2]}(\overline{zf^o}\oplus\overline{zf^e})=\phi_1\overline{zf^o}+\phi_2\overline{zf^e}.
\end{align*} Similarly, we obtain  $M_{\bar{z}^2}C(f)=M_{\bar{z}^2}M_{[\phi_1,\phi_2]}(z\overline{f^o}\oplus z\overline{f^e}) = \phi_1\overline{zf^o}+\phi_2\overline{zf^e}$. This completes the proof.
$M_{\bar{z}^2}C(f)=M_{\bar{z}^2}M_{[\phi_1,\phi_2]}(z\overline{f^o}\oplus z\overline{f^e}) = \phi_1\overline{zf^o}+\phi_2\overline{zf^e}$. This completes the proof.
As a consequence of the above theorem, we characterize all conjugations C intertwining the operators ![]() $M_{z^2}$,
$M_{z^2}$, ![]() $M_{\bar{z}^2}$ in L 2 in terms of J as follows:
$M_{\bar{z}^2}$ in L 2 in terms of J as follows:
Corollary 4.2. Let C be a conjugation on L 2 such that ![]() $CM_{z^2}=M_{\bar{z}^2}C$, then
$CM_{z^2}=M_{\bar{z}^2}C$, then ![]() $C=M_{[\psi_1,\psi_2]}J$ for
$C=M_{[\psi_1,\psi_2]}J$ for ![]() $\psi_1,\psi_2\in L^\infty$ with
$\psi_1,\psi_2\in L^\infty$ with ![]() $\psi_1^o= \psi_2^o$ and
$\psi_1^o= \psi_2^o$ and ![]() $|\psi_1|^2+|\psi_2|^2=2$. Conversely, any conjugation C of the form
$|\psi_1|^2+|\psi_2|^2=2$. Conversely, any conjugation C of the form ![]() $M_{[\psi_1,\psi_2]}J$ for
$M_{[\psi_1,\psi_2]}J$ for ![]() $\psi_1,\psi_2 \in L^\infty$ satisfies
$\psi_1,\psi_2 \in L^\infty$ satisfies ![]() $CM_{z^2}=M_{\bar{z}^2}C$.
$CM_{z^2}=M_{\bar{z}^2}C$.
Proof. By definition of ![]() $\mathscr{C}_{z^2}$ it follows that
$\mathscr{C}_{z^2}$ it follows that ![]() $\mathscr{C}_{z^2} = M_z J$. Therefore, by using Theorem 4.1, we conclude
$\mathscr{C}_{z^2} = M_z J$. Therefore, by using Theorem 4.1, we conclude ![]() $C=M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2}$, where
$C=M_{[\phi_1,\phi_2]} \mathscr{C}_{z^2}$, where ![]() $\phi_1^e= \phi_2^e$ and
$\phi_1^e= \phi_2^e$ and ![]() $|\phi_1|^2+|\phi_2|^2=2$. Note that
$|\phi_1|^2+|\phi_2|^2=2$. Note that ![]() $M_{[\phi_1,\phi_2]}M_z= M_{[z\phi_2,z\phi_1]}$ and hence
$M_{[\phi_1,\phi_2]}M_z= M_{[z\phi_2,z\phi_1]}$ and hence ![]() $C=M_{[\psi_1,\psi_2]}J$, where
$C=M_{[\psi_1,\psi_2]}J$, where ![]() $\psi_1 (=z\phi_2) , \psi_2 (= z\phi_1)\in L^\infty$. Moreover, the involutive property of the conjugation C implies
$\psi_1 (=z\phi_2) , \psi_2 (= z\phi_1)\in L^\infty$. Moreover, the involutive property of the conjugation C implies ![]() $\psi_1^o= \psi_2^o$, and since
$\psi_1^o= \psi_2^o$, and since ![]() $M_{[\psi_1,\psi_2]}$ is unitary, then we have
$M_{[\psi_1,\psi_2]}$ is unitary, then we have ![]() $|\psi_1|^2+|\psi_2|^2=2$. The converse is straightforward.
$|\psi_1|^2+|\psi_2|^2=2$. The converse is straightforward.
Remark 4.3. Note that, the conditions (4.2) in Theorem 4.1 after substituting ![]() $\mathscr{C}_{z^2} = M_z J$ and
$\mathscr{C}_{z^2} = M_z J$ and ![]() $\psi_1 =z\phi_2 , \psi_2= z\phi_1$, change to:
$\psi_1 =z\phi_2 , \psi_2= z\phi_1$, change to:
 \begin{equation}
\begin{cases}
|\psi_2^o|^2+|\psi_2^e|^2=1 ~,~ |\psi_2^o|^2+|\psi_2^e|^2=1,\\
|\psi_2^o|^2+|\psi_1^e|^2=1 ~,~ |\psi_2^e|^2 + |\psi_1^o|^2=1,\\
\bar{\psi_2^o}\psi_1^e+\bar{\psi_2^e}\psi_1^o=0,~ \bar{\psi_2^e}\psi_2^o+\bar{\psi_1^o}\psi_1^e=0.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\psi_2^o|^2+|\psi_2^e|^2=1 ~,~ |\psi_2^o|^2+|\psi_2^e|^2=1,\\
|\psi_2^o|^2+|\psi_1^e|^2=1 ~,~ |\psi_2^e|^2 + |\psi_1^o|^2=1,\\
\bar{\psi_2^o}\psi_1^e+\bar{\psi_2^e}\psi_1^o=0,~ \bar{\psi_2^e}\psi_2^o+\bar{\psi_1^o}\psi_1^e=0.
\end{cases}
\end{equation} It should be noted that if we combine the above set of conditions, it reduces to the single condition ![]() $|\psi_1|^2+|\psi_2|^2=2$ obtained in Corollary 4.2. The usefulness of the conditions in (4.4) will be realized in a later section.
$|\psi_1|^2+|\psi_2|^2=2$ obtained in Corollary 4.2. The usefulness of the conditions in (4.4) will be realized in a later section.
Remark 4.4. It is important to note that if we assume ![]() $\psi_1 =\psi_2$ in Corollary (4.2), then
$\psi_1 =\psi_2$ in Corollary (4.2), then ![]() $C=M_{\psi_1}J$ intertwining the operators Mz,
$C=M_{\psi_1}J$ intertwining the operators Mz, ![]() $M_{\bar{z}}$ and hence intertwining the operators
$M_{\bar{z}}$ and hence intertwining the operators ![]() $M_{z^2}$,
$M_{z^2}$, ![]() $M_{\bar{z}^2}$ as well in L 2. On the other hand, if
$M_{\bar{z}^2}$ as well in L 2. On the other hand, if ![]() $\psi_1 \neq \psi_2$, then
$\psi_1 \neq \psi_2$, then ![]() $C=M_{[\psi_1,\psi_2]}J$ intertwining the operators
$C=M_{[\psi_1,\psi_2]}J$ intertwining the operators ![]() $M_{z^2}$,
$M_{z^2}$, ![]() $M_{\bar{z}^2}$ but not intertwining the operators Mz and
$M_{\bar{z}^2}$ but not intertwining the operators Mz and ![]() $M_{\bar{z}}$ in L 2.
$M_{\bar{z}}$ in L 2.
According to the previous discussion, our next aim is to characterize all the conjugations commuting with ![]() $M_{z^2}$. For instance, the conjugation
$M_{z^2}$. For instance, the conjugation ![]() $\mathscr{C}_{z^2}^\star$ (see (3.4)) commutes with
$\mathscr{C}_{z^2}^\star$ (see (3.4)) commutes with ![]() $M_{z^2}$. To be more specific, for
$M_{z^2}$. To be more specific, for  $f(z)=\sum\limits_{k=-\infty}^{\infty}a_nz^n\in L^2$, the action of
$f(z)=\sum\limits_{k=-\infty}^{\infty}a_nz^n\in L^2$, the action of ![]() $\mathscr{C}_{z^2}^\star$ is given by:
$\mathscr{C}_{z^2}^\star$ is given by:
 \begin{align*}
\mathscr{C}_{z^2}^\star(\sum_{k=-\infty}^{\infty}a_nz^n)=& \sum_{k=-\infty}^{\infty}\bar{a}_{2n}z^{2n+1} + \sum_{k=-\infty}^{\infty}\bar{a}_{2n+1}z^{2n}~\implies~
\mathscr{C}_{z^2}^\star(f(z))\\ =& z\overline{f^e(\bar{z})} +\bar{z}\overline{f^o(\bar{z})}.
\end{align*}
\begin{align*}
\mathscr{C}_{z^2}^\star(\sum_{k=-\infty}^{\infty}a_nz^n)=& \sum_{k=-\infty}^{\infty}\bar{a}_{2n}z^{2n+1} + \sum_{k=-\infty}^{\infty}\bar{a}_{2n+1}z^{2n}~\implies~
\mathscr{C}_{z^2}^\star(f(z))\\ =& z\overline{f^e(\bar{z})} +\bar{z}\overline{f^o(\bar{z})}.
\end{align*} Now, we have the following theorem concerning ![]() $M_{z^2}$-commuting conjugations.
$M_{z^2}$-commuting conjugations.
Theorem 4.5. If C is a conjugation on ![]() $L^2(\mathbb{T})$ such that
$L^2(\mathbb{T})$ such that ![]() $CM_{z^2}=M_{z^2}C$, then there exist
$CM_{z^2}=M_{z^2}C$, then there exist ![]() $\zeta_1,\zeta_2 \in L^\infty$ satisfying
$\zeta_1,\zeta_2 \in L^\infty$ satisfying  $|\zeta_1|^2+|\zeta_2|^2=2,
|\bar{z}\zeta_1^o+z\zeta_2^e|^2+|\bar{z}\zeta_1^e+z\zeta_2^o|^2=2, \zeta_2^e(\bar{z})=\zeta_1^e(z), \zeta_2^o(\bar{z})=z^2\zeta_2^0(z), z^2\zeta_1^o(\bar{z})=\zeta_1^o(z)$ such that:
$|\zeta_1|^2+|\zeta_2|^2=2,
|\bar{z}\zeta_1^o+z\zeta_2^e|^2+|\bar{z}\zeta_1^e+z\zeta_2^o|^2=2, \zeta_2^e(\bar{z})=\zeta_1^e(z), \zeta_2^o(\bar{z})=z^2\zeta_2^0(z), z^2\zeta_1^o(\bar{z})=\zeta_1^o(z)$ such that:
Conversely, any conjugation C of the form ![]() $M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$ for
$M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$ for ![]() $\zeta_1,\zeta_2 \in L^\infty$ commutes with
$\zeta_1,\zeta_2 \in L^\infty$ commutes with ![]() $M_{z^2}$.
$M_{z^2}$.
Proof. Let C be a conjugation on ![]() $L^2(\mathbb{T})$ such that
$L^2(\mathbb{T})$ such that ![]() $CM_{z^2}=M_{z^2}C$. Since
$CM_{z^2}=M_{z^2}C$. Since ![]() $\mathscr{C}_{z^2}^\star M_{z^2}=M_{z^2}\mathscr{C}_{z^2}^\star$, then the unitary operator
$\mathscr{C}_{z^2}^\star M_{z^2}=M_{z^2}\mathscr{C}_{z^2}^\star$, then the unitary operator ![]() $C\circ \mathscr{C}_{z^2}^\star$ also commutes with
$C\circ \mathscr{C}_{z^2}^\star$ also commutes with ![]() $M_{z^2}$ in
$M_{z^2}$ in ![]() $L^2(\mathbb{T})$ . Therefore by applying Theorem 2.2, there exist
$L^2(\mathbb{T})$ . Therefore by applying Theorem 2.2, there exist ![]() $\zeta_1,\zeta_2\in L^\infty(\mathbb{T})$ such that
$\zeta_1,\zeta_2\in L^\infty(\mathbb{T})$ such that ![]() $C\circ \mathscr{C}_{z^2}^\star = M_{[\zeta_1,\zeta_2]}$. Now by considering the decomposition
$C\circ \mathscr{C}_{z^2}^\star = M_{[\zeta_1,\zeta_2]}$. Now by considering the decomposition ![]() $L^2(\mathbb{T})=\mathcal{H}_1(1,z^2) \oplus \mathcal{H}_2(z,z^2)$, we have the following block-matrix representation of
$L^2(\mathbb{T})=\mathcal{H}_1(1,z^2) \oplus \mathcal{H}_2(z,z^2)$, we have the following block-matrix representation of ![]() $M_{[\zeta_1,\zeta_2]}$:
$M_{[\zeta_1,\zeta_2]}$:
 \begin{equation*}
M_{[\zeta_1,\zeta_2]}=
\begin{bmatrix}
M_{\zeta_1^e} && M_{\zeta_2^o}\\
\\
M_{\zeta_1^o} && M_{\zeta_2^e}\\
\end{bmatrix} \text{,~and~hence~}
M_{[\zeta_1,\zeta_2]}^*=
\begin{bmatrix}
M_{\bar{\zeta_1^e}} && M_{\bar{\zeta_1^o}}\\
\\
M_{\bar{\zeta_2^0}} && M_{\bar{\zeta_2^e}}\\
\end{bmatrix}.
\end{equation*}
\begin{equation*}
M_{[\zeta_1,\zeta_2]}=
\begin{bmatrix}
M_{\zeta_1^e} && M_{\zeta_2^o}\\
\\
M_{\zeta_1^o} && M_{\zeta_2^e}\\
\end{bmatrix} \text{,~and~hence~}
M_{[\zeta_1,\zeta_2]}^*=
\begin{bmatrix}
M_{\bar{\zeta_1^e}} && M_{\bar{\zeta_1^o}}\\
\\
M_{\bar{\zeta_2^0}} && M_{\bar{\zeta_2^e}}\\
\end{bmatrix}.
\end{equation*} Using the fact that ![]() $M_{[\zeta_1,\zeta_2]}$ is a unitary operator we obtain the following conditions:
$M_{[\zeta_1,\zeta_2]}$ is a unitary operator we obtain the following conditions:
 \begin{equation}
\begin{cases}
|\zeta_1^e|^2+|\zeta_1^o|^2=1,~ |\zeta_1^e|^2+|\zeta_1^o|^2=1,\\
|\zeta_1^e|^2+|\zeta_2^o|^2=1,~ |\zeta_1^o|^2 + |\zeta_2^e|^2=1,\\
\bar{\zeta_1^e}\zeta_2^o+\bar{\zeta_1^o}\zeta_2^e=0,~ \bar{\zeta_1^o}\zeta_1^e+\bar{\zeta_2^e}\zeta_2^o=0,
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\zeta_1^e|^2+|\zeta_1^o|^2=1,~ |\zeta_1^e|^2+|\zeta_1^o|^2=1,\\
|\zeta_1^e|^2+|\zeta_2^o|^2=1,~ |\zeta_1^o|^2 + |\zeta_2^e|^2=1,\\
\bar{\zeta_1^e}\zeta_2^o+\bar{\zeta_1^o}\zeta_2^e=0,~ \bar{\zeta_1^o}\zeta_1^e+\bar{\zeta_2^e}\zeta_2^o=0,
\end{cases}
\end{equation}which by simplifying, becomes:
 \begin{equation*}
\begin{cases}
|\zeta_1|^2+|\zeta_2|^2=2,\\
|\bar{z}\zeta_1^o+z\zeta_2^e|^2+|\bar{z}\zeta_1^e+z\zeta_2^o|^2=2.
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
|\zeta_1|^2+|\zeta_2|^2=2,\\
|\bar{z}\zeta_1^o+z\zeta_2^e|^2+|\bar{z}\zeta_1^e+z\zeta_2^o|^2=2.
\end{cases}
\end{equation*}Moreover, the involutive property of the conjugation C implies:
 \begin{equation*}
\mathscr{C}_{z^2}^\star M_{[\zeta_1,\zeta_2]} \mathscr{C}_{z^2}^\star = M_{[\zeta_1,\zeta_2]}^*,
\end{equation*}
\begin{equation*}
\mathscr{C}_{z^2}^\star M_{[\zeta_1,\zeta_2]} \mathscr{C}_{z^2}^\star = M_{[\zeta_1,\zeta_2]}^*,
\end{equation*} which by applying on the basis vectors 1 and z, we get ![]() $\zeta_2^e(\bar{z})=\zeta_1^e(z)$,
$\zeta_2^e(\bar{z})=\zeta_1^e(z)$, ![]() $\zeta_2^o(\bar{z})=z^2\zeta_2^0(z)$ and
$\zeta_2^o(\bar{z})=z^2\zeta_2^0(z)$ and ![]() $z^2\zeta_1^o(\bar{z})=\zeta_1^o(z)$,
$z^2\zeta_1^o(\bar{z})=\zeta_1^o(z)$, ![]() $\zeta_1^e(\bar{z}) =\zeta_2^e(z)$, respectively.
$\zeta_1^e(\bar{z}) =\zeta_2^e(z)$, respectively.
Conversely, if ![]() $C=M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$ for
$C=M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$ for ![]() $\zeta_1,\zeta_2 \in L^\infty$ , then it is easy to verify that
$\zeta_1,\zeta_2 \in L^\infty$ , then it is easy to verify that ![]() $CM_{z^2}=M_{z^2}C$. This completes the proof.
$CM_{z^2}=M_{z^2}C$. This completes the proof.
Remark 4.6. It is interesting to note that the conjugation ![]() $\mathscr{C}_{z^2}^\star$ commutes with
$\mathscr{C}_{z^2}^\star$ commutes with ![]() $M_{z^2}$ but not with Mz. But in the above Theorem 4.5, we characterize
$M_{z^2}$ but not with Mz. But in the above Theorem 4.5, we characterize ![]() $M_{z^2}$-commuting conjugations in terms of
$M_{z^2}$-commuting conjugations in terms of ![]() $M_{[\zeta_1,\zeta_2]}$ and
$M_{[\zeta_1,\zeta_2]}$ and ![]() $\mathscr{C}_{z^2}^\star$, where the composition operator
$\mathscr{C}_{z^2}^\star$, where the composition operator ![]() $M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$ may commutes with Mz.
$M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$ may commutes with Mz.
In general, it is quite difficult to distinguish between the class of conjugations commuting with Mz and the class of conjugations not commuting with Mz inside ![]() $M_{z^2}$-commuting conjugations. To get a better understanding of the same, we revisit the study of
$M_{z^2}$-commuting conjugations. To get a better understanding of the same, we revisit the study of ![]() $M_{z^2}$-commuting conjugations in the following corollary.
$M_{z^2}$-commuting conjugations in the following corollary.
Corollary 4.7. Any ![]() $ M_{z^2}$-commuting conjugation C on L 2, there exist two
$ M_{z^2}$-commuting conjugation C on L 2, there exist two ![]() $L^\infty$-functions
$L^\infty$-functions ![]() $\xi_1,\xi_2$ on
$\xi_1,\xi_2$ on ![]() $\mathbb{T}$ such that
$\mathbb{T}$ such that ![]() $C=M_{[\xi_1,\xi_2]}J^\star$, where ξ 1 and ξ 2 satisfy
$C=M_{[\xi_1,\xi_2]}J^\star$, where ξ 1 and ξ 2 satisfy ![]() $|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \text{and}~ \xi_2^e(\bar{z})=\xi_2^e(z)$. Conversely, any conjugation C of the form
$|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \text{and}~ \xi_2^e(\bar{z})=\xi_2^e(z)$. Conversely, any conjugation C of the form ![]() $M_{[\xi_1,\xi_2]}J^\star$ for
$M_{[\xi_1,\xi_2]}J^\star$ for ![]() $\xi_1,\xi_2 \in L^\infty $ commutes with
$\xi_1,\xi_2 \in L^\infty $ commutes with ![]() $M_{z^2}$.
$M_{z^2}$.
Proof. Let ![]() $C:L^2(\mathbb{T})\to L^2(\mathbb{T})$ be a conjugation such that
$C:L^2(\mathbb{T})\to L^2(\mathbb{T})$ be a conjugation such that ![]() $CM_{z^2}=M_{z^2}C$. Then by using the above Theorem 4.5, we get two
$CM_{z^2}=M_{z^2}C$. Then by using the above Theorem 4.5, we get two ![]() $L^\infty$-functions
$L^\infty$-functions ![]() $\zeta_1,\zeta_2$ such that
$\zeta_1,\zeta_2$ such that ![]() $C= M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$, and
$C= M_{[\zeta_1,\zeta_2]}\mathscr{C}_{z^2}^\star$, and
 \begin{equation}
\begin{cases}
|\zeta_1|^2+|\zeta_2|^2=2,
|\bar{z}\zeta_1^o+z\zeta_2^e|^2+|\bar{z}\zeta_1^e+z\zeta_2^o|^2=2,\\
\zeta_2^e(\bar{z})=\zeta_1^e(z), \zeta_2^o(\bar{z})=z^2\zeta_2^0(z), z^2\zeta_1^o(\bar{z})=\zeta_1^o(z).
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\zeta_1|^2+|\zeta_2|^2=2,
|\bar{z}\zeta_1^o+z\zeta_2^e|^2+|\bar{z}\zeta_1^e+z\zeta_2^o|^2=2,\\
\zeta_2^e(\bar{z})=\zeta_1^e(z), \zeta_2^o(\bar{z})=z^2\zeta_2^0(z), z^2\zeta_1^o(\bar{z})=\zeta_1^o(z).
\end{cases}
\end{equation} Moreover, for any ![]() $f(=f^e\oplus f^o)\in L^2$ and
$f(=f^e\oplus f^o)\in L^2$ and ![]() $z\in \mathbb{T}$, we have
$z\in \mathbb{T}$, we have
 \begin{equation*}(\mathscr{C}_{z^2}^\star f) (z)= z\overline{f^e(\bar{z})}+\bar{z}\overline{f^o(\bar{z})}=\bar{z}\overline{f^o(\bar{z})} \oplus z\overline{f^e(\bar{z})} =(M_{[z,\bar{z}]}J^\star f)(z) ,\end{equation*}
\begin{equation*}(\mathscr{C}_{z^2}^\star f) (z)= z\overline{f^e(\bar{z})}+\bar{z}\overline{f^o(\bar{z})}=\bar{z}\overline{f^o(\bar{z})} \oplus z\overline{f^e(\bar{z})} =(M_{[z,\bar{z}]}J^\star f)(z) ,\end{equation*} and hence ![]() $\mathscr{C}_{z^2}^\star = M_{[z,\bar{z}]}J^\star $ which immediately implies:
$\mathscr{C}_{z^2}^\star = M_{[z,\bar{z}]}J^\star $ which immediately implies:
where ![]() $\xi_1=z\zeta_2$ and
$\xi_1=z\zeta_2$ and ![]() $\xi_2=\bar{z}\zeta_1$. Next by identifying the relation between
$\xi_2=\bar{z}\zeta_1$. Next by identifying the relation between ![]() $\{\zeta_1,\zeta_2\}$ and
$\{\zeta_1,\zeta_2\}$ and ![]() $\{\xi_1,\xi_2\}$ we obtain:
$\{\xi_1,\xi_2\}$ we obtain:
 \begin{equation}
\begin{cases}
\zeta_1^e = z\xi_2^o ,~ \zeta_1^o = z\xi_2^e,\\
\zeta_2^e = \bar{z}\xi_1^o ,~ \zeta_2^o = \bar{z}\xi_1^e.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
\zeta_1^e = z\xi_2^o ,~ \zeta_1^o = z\xi_2^e,\\
\zeta_2^e = \bar{z}\xi_1^o ,~ \zeta_2^o = \bar{z}\xi_1^e.
\end{cases}
\end{equation}Thus, the conditions in (4.6) becomes:
 \begin{equation}
\begin{cases}
|\xi_1|^2+|\xi_2|^2=2, |\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2, \\
z\xi_1^o(\bar{z})=z\xi_2^o(z), z\xi_1^e(\bar{z})=z^2\bar{z}\xi_1^e(z), z^2\bar{z}\xi_2^e(\bar{z})=z\xi_2^e(z),
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\xi_1|^2+|\xi_2|^2=2, |\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2, \\
z\xi_1^o(\bar{z})=z\xi_2^o(z), z\xi_1^e(\bar{z})=z^2\bar{z}\xi_1^e(z), z^2\bar{z}\xi_2^e(\bar{z})=z\xi_2^e(z),
\end{cases}
\end{equation}which by simple modification reduces to:
 \begin{equation}
\begin{cases}
|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2, \\
\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z).
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2, \\
\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z).
\end{cases}
\end{equation} For the converse, it is easy to verify that for any conjugation C on L 2 having the form ![]() $C=M_{[\xi_1,\xi_2]}J^\star$ commutes with
$C=M_{[\xi_1,\xi_2]}J^\star$ commutes with ![]() $M_{z^2}$. This completes the proof.
$M_{z^2}$. This completes the proof.
Remark 4.8. It is important to observe that the conditions ![]() $|\xi_1|^2+|\xi_2|^2=2$ and
$|\xi_1|^2+|\xi_2|^2=2$ and ![]() $|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2 $ in (4.10) of the above Corollary 4.7 can be reduced from the original conditions (4.5) of Theorem 4.5. Going further, one should always remember that the original explicit conditions behind the above two reduced conditions are:
$|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2 $ in (4.10) of the above Corollary 4.7 can be reduced from the original conditions (4.5) of Theorem 4.5. Going further, one should always remember that the original explicit conditions behind the above two reduced conditions are:
 \begin{equation}
\begin{cases}
|\xi_1^e|^2+|\xi_1^o|^2=1,~ |\xi_1^e|^2+|\xi_1^o|^2=1,\\
|\xi_1^e|^2+|\xi_2^o|^2=1,~ |\xi_1^o|^2 + |\xi_2^e|^2=1,\\
\bar{\xi_2^o}\xi_1^e+\bar{\xi_2^e}\xi_1^o=0,~ \bar{\xi_2^e}\xi_2^o+\bar{\xi_1^o}\xi_1^e=0.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
|\xi_1^e|^2+|\xi_1^o|^2=1,~ |\xi_1^e|^2+|\xi_1^o|^2=1,\\
|\xi_1^e|^2+|\xi_2^o|^2=1,~ |\xi_1^o|^2 + |\xi_2^e|^2=1,\\
\bar{\xi_2^o}\xi_1^e+\bar{\xi_2^e}\xi_1^o=0,~ \bar{\xi_2^e}\xi_2^o+\bar{\xi_1^o}\xi_1^e=0.
\end{cases}
\end{equation} Now, we are in a position to distinguish between the class of conjugations commuting with Mz and the class of conjugations not commuting with Mz inside ![]() $M_{z^2}$-commuting conjugations with the help of the above Corollary 4.7.
$M_{z^2}$-commuting conjugations with the help of the above Corollary 4.7.
• If the two
 $L^\infty$-functions ξ 1 and ξ 2 appearing in the representation of
$L^\infty$-functions ξ 1 and ξ 2 appearing in the representation of  $M_{z^2}$-commuting conjugation C as described in 4.7 becomes identical, that is, if
$M_{z^2}$-commuting conjugation C as described in 4.7 becomes identical, that is, if  $\xi_1=\xi_2$, then the conclusion can be drawn that C actually commutes with Mz. Conversely, if C commutes with Mz, then by using Corollary 4.7 and Remark 2.3, we conclude
$\xi_1=\xi_2$, then the conclusion can be drawn that C actually commutes with Mz. Conversely, if C commutes with Mz, then by using Corollary 4.7 and Remark 2.3, we conclude  $C=M_{[\xi,\xi]}J^\star$, where
$C=M_{[\xi,\xi]}J^\star$, where  $\xi \in L^\infty $ satisfying
$\xi \in L^\infty $ satisfying  $|\xi|^2+|\xi|^2=2,\xi^o(\bar{z})=\xi^o(z), \xi^e(\bar{z})=\xi^e(z), $ and
$|\xi|^2+|\xi|^2=2,\xi^o(\bar{z})=\xi^o(z), \xi^e(\bar{z})=\xi^e(z), $ and  $\xi^e(\bar{z})=\xi^e(z)$ which implies
$\xi^e(\bar{z})=\xi^e(z)$ which implies  $C=M_{\xi}J^\star$, where
$C=M_{\xi}J^\star$, where  $\xi \in L^\infty $ such that
$\xi \in L^\infty $ such that  $|\xi|=1$ and
$|\xi|=1$ and  $\xi(z)=\xi(\bar{z})$ and it is consistent with the condition obtained in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10].
$\xi(z)=\xi(\bar{z})$ and it is consistent with the condition obtained in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10].• As a matter of fact, if
 $\xi_1 \neq \xi_2$, then
$\xi_1 \neq \xi_2$, then  $C=M_{[\xi_1,\xi_2]}J^\star$ commutes with
$C=M_{[\xi_1,\xi_2]}J^\star$ commutes with  $M_{z^2}$ but not with Mz. Conversely, if C commutes only with
$M_{z^2}$ but not with Mz. Conversely, if C commutes only with  $M_{z^2}$, then there exist
$M_{z^2}$, then there exist  $\xi_1 \neq \xi_2$ satisfying:
$\xi_1 \neq \xi_2$ satisfying:
 \begin{align*}
\hspace{0.5in} |\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,
\xi_1^o(\bar{z})=&\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z),\\& ~\text{and}~ \xi_2^e(\bar{z})=\xi_2^e(z),
\end{align*}
\begin{align*}
\hspace{0.5in} |\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,
\xi_1^o(\bar{z})=&\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z),\\& ~\text{and}~ \xi_2^e(\bar{z})=\xi_2^e(z),
\end{align*}such that
 $C=M_{[\xi_1,\xi_2]}J^\star$ and we call such type of conjugations as
$C=M_{[\xi_1,\xi_2]}J^\star$ and we call such type of conjugations as  $only~M_{z^2}$-commuting conjugations.
$only~M_{z^2}$-commuting conjugations.
Therefore, the above discussions completely describe the class of conjugations that commute with ![]() $M_{z^2}$ in L 2-space.
$M_{z^2}$ in L 2-space.
5. The class of conjugations that keep invariant various subspaces of  $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
Our main aim in this section is to study the behaviour of two special classes of conjugations, namely ![]() $M_{z^2},M_{\bar{z}^2}$-intertwining, and
$M_{z^2},M_{\bar{z}^2}$-intertwining, and ![]() $M_{z^2}$-commuting conjugations that keep invariant various subspaces of L 2 like the Hardy space H 2, model spaces and shift-invariant subspaces. The study of
$M_{z^2}$-commuting conjugations that keep invariant various subspaces of L 2 like the Hardy space H 2, model spaces and shift-invariant subspaces. The study of ![]() $M_{z},M_{\bar{z}}$-intertwining, and Mz-commuting conjugations preserving H 2, model spaces and shift-invariant subspaces have been done recently in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10]. The significant difference between our study and the study in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10] is that we characterize
$M_{z},M_{\bar{z}}$-intertwining, and Mz-commuting conjugations preserving H 2, model spaces and shift-invariant subspaces have been done recently in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10]. The significant difference between our study and the study in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10] is that we characterize ![]() $only~M_{z^2}$-commuting and
$only~M_{z^2}$-commuting and ![]() $M_{z^2},M_{\bar{z}^2}$-intertwining (but not
$M_{z^2},M_{\bar{z}^2}$-intertwining (but not ![]() $M_{z},M_{\bar{z}}$-intertwining ) conjugations preserving the above mentioned subspaces.
$M_{z},M_{\bar{z}}$-intertwining ) conjugations preserving the above mentioned subspaces.
5.1. Hardy space preserving conjugations
We have already identified the class of conjugations that intertwine the operators ![]() $M_{z^2}$,
$M_{z^2}$, ![]() $M_{\bar{z}^2}$ and also the class of conjugations that commute with
$M_{\bar{z}^2}$ and also the class of conjugations that commute with ![]() $M_{z^2}$ in terms of known conjugations in the previous section. Note that the involutive property of a conjugation guarantees that if H 2 is invariant under any conjugation C in L 2, then
$M_{z^2}$ in terms of known conjugations in the previous section. Note that the involutive property of a conjugation guarantees that if H 2 is invariant under any conjugation C in L 2, then ![]() $C(H^2)=H^2$. Now, we will discuss the class of
$C(H^2)=H^2$. Now, we will discuss the class of ![]() $only~M_{z^2}-commuting$ conjugations that keep the Hardy space invariant.
$only~M_{z^2}-commuting$ conjugations that keep the Hardy space invariant.
Theorem 5.1. Let C be a ‘![]() $only~M_{z^2}-commuting$’ conjugation on L 2 such that
$only~M_{z^2}-commuting$’ conjugation on L 2 such that ![]() $C(H^2)\subset H^2$, then
$C(H^2)\subset H^2$, then ![]() $C=M_{[\xi_1,\xi_2]}J^\star$, where
$C=M_{[\xi_1,\xi_2]}J^\star$, where
(i)
 $\xi_1=a_0+a_1z$,
$\xi_1=a_0+a_1z$,  $\xi_2 =a_1\bar{z}+b_0$ for some
$\xi_2 =a_1\bar{z}+b_0$ for some  $a_0,a_1,b_0 \in \mathbb{C}, $ and
$a_0,a_1,b_0 \in \mathbb{C}, $ and(ii)
 $|a_0|^2+|a_1|^2=1,|b_0|^2+|a_1|^2=1,a_0\bar{a_1}+a_1\bar{b}_0=0.$
$|a_0|^2+|a_1|^2=1,|b_0|^2+|a_1|^2=1,a_0\bar{a_1}+a_1\bar{b}_0=0.$
Proof. Let C be a ![]() $only~M_{z^2}-commuting$ conjugation on L 2. Then by Corollary 4.7, there exist
$only~M_{z^2}-commuting$ conjugation on L 2. Then by Corollary 4.7, there exist ![]() $\xi_1,\xi_2\in L^\infty$ such that
$\xi_1,\xi_2\in L^\infty$ such that ![]() $C=M_{[\xi_1,\xi_2]}J^\star $, where
$C=M_{[\xi_1,\xi_2]}J^\star $, where ![]() $|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z)$. Moreover,
$|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z)$. Moreover, ![]() $C(1)\in H^2$ and
$C(1)\in H^2$ and ![]() $C(z)\in H^2$ implies
$C(z)\in H^2$ implies ![]() $\xi_1\in H^\infty$ and
$\xi_1\in H^\infty$ and ![]() $z\xi_2 \in H^\infty$ respectively. Suppose
$z\xi_2 \in H^\infty$ respectively. Suppose  $\xi_1=\sum\limits_{k=0}^{\infty}a_kz^k $ and
$\xi_1=\sum\limits_{k=0}^{\infty}a_kz^k $ and  $\xi_2 =\sum\limits_{k=-1}^{\infty}b_kz^k$. Now, combining the facts
$\xi_2 =\sum\limits_{k=-1}^{\infty}b_kz^k$. Now, combining the facts ![]() $\xi_1^e\in H^\infty$ and
$\xi_1^e\in H^\infty$ and ![]() $\xi_1^e(\bar{z})=\xi_1^e(z)$, we conclude
$\xi_1^e(\bar{z})=\xi_1^e(z)$, we conclude ![]() $ \xi_1^e= constant $. Moreover, the condition
$ \xi_1^e= constant $. Moreover, the condition ![]() $\xi_2^e(\bar{z})=\xi_2^e(z)$ implies
$\xi_2^e(\bar{z})=\xi_2^e(z)$ implies ![]() $\xi_2^e= constant $ and the condition
$\xi_2^e= constant $ and the condition ![]() $\xi_1^o(\bar{z})=\xi_2^o(z)$ implies
$\xi_1^o(\bar{z})=\xi_2^o(z)$ implies ![]() $\xi_1^o(z)=a_1z$ and
$\xi_1^o(z)=a_1z$ and ![]() $\xi_2^o(z)=b_{-1}\bar{z}$ with
$\xi_2^o(z)=b_{-1}\bar{z}$ with ![]() $a_1=b_{-1}$, which immediately yield
$a_1=b_{-1}$, which immediately yield ![]() $\xi_1=a_0+a_1z$ and
$\xi_1=a_0+a_1z$ and ![]() $\xi_2 =a_1\bar{z}+b_0$ for some
$\xi_2 =a_1\bar{z}+b_0$ for some ![]() $a_0,a_1,b_0 \in \mathbb{C} $. It is important to note that, we obtain the conditions
$a_0,a_1,b_0 \in \mathbb{C} $. It is important to note that, we obtain the conditions ![]() $|\xi_1|^2+|\xi_2|^2=2$ and
$|\xi_1|^2+|\xi_2|^2=2$ and ![]() $|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2$ by reducing the conditions listed in (4.11) in Remark 4.8 and hence we get the following relations between a 0, a 1 and b 0
$|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2$ by reducing the conditions listed in (4.11) in Remark 4.8 and hence we get the following relations between a 0, a 1 and b 0
This completes the proof.
5.2. Model space preserving conjugations
In this subsection, we characterize ![]() $M_{z^2}$-commuting and Mz,
$M_{z^2}$-commuting and Mz, ![]() $M_{\bar{z}}$-intertwining conjugations preserving model spaces in terms of
$M_{\bar{z}}$-intertwining conjugations preserving model spaces in terms of ![]() $\mathscr{C}_\theta$. The following two propositions will be useful to prove our main results.
$\mathscr{C}_\theta$. The following two propositions will be useful to prove our main results.
Proposition 5.2. If C is a conjugation on L 2 such that ![]() $CM_{z^2}=M_{\bar{z}^2}C$, then
$CM_{z^2}=M_{\bar{z}^2}C$, then ![]() $M_{z}CM_{\bar{z}}$ is also a conjugation on L 2 intertwining
$M_{z}CM_{\bar{z}}$ is also a conjugation on L 2 intertwining ![]() $M_{z^2}, M_{\bar{z}^2}$, and
$M_{z^2}, M_{\bar{z}^2}$, and  $M_{z}CM_{\bar{z}}=M_{[z^2\psi_2 , z^2\psi_1 ]}J$ for some
$M_{z}CM_{\bar{z}}=M_{[z^2\psi_2 , z^2\psi_1 ]}J$ for some ![]() $\psi_1,\psi_2 \in L^\infty$ satisfying
$\psi_1,\psi_2 \in L^\infty$ satisfying ![]() $\psi_1^o= \psi_2^o$ and
$\psi_1^o= \psi_2^o$ and ![]() $|\psi_1|^2+|\psi_2|^2=2$.
$|\psi_1|^2+|\psi_2|^2=2$.
Proof. Suppose C is a conjugation on L 2 such that ![]() $CM_{z^2}=M_{\bar{z}^2}C$, then by Corollary 4.2, there exist
$CM_{z^2}=M_{\bar{z}^2}C$, then by Corollary 4.2, there exist ![]() $\psi_1,\psi_2 \in L^\infty$ such that
$\psi_1,\psi_2 \in L^\infty$ such that ![]() $C=M_{[\psi_1,\psi_2]}J$, where
$C=M_{[\psi_1,\psi_2]}J$, where ![]() $\psi_1^o= \psi_2^o$ and
$\psi_1^o= \psi_2^o$ and ![]() $|\psi_1|^2+|\psi_2|^2=2$. It is easy to see that
$|\psi_1|^2+|\psi_2|^2=2$. It is easy to see that ![]() $M_{z}CM_{\bar{z}}$ is a conjugation on L 2 and
$M_{z}CM_{\bar{z}}$ is a conjugation on L 2 and ![]() $M_{z}CM_{\bar{z}}M_{z}=M_{\bar{z}}M_{z}CM_{\bar{z}}$. Therefore, by applying Corollary 4.2 again, we have
$M_{z}CM_{\bar{z}}M_{z}=M_{\bar{z}}M_{z}CM_{\bar{z}}$. Therefore, by applying Corollary 4.2 again, we have ![]() $M_{z}CM_{\bar{z}}=M_{[\vartheta_1,\vartheta_2]}J$ for some
$M_{z}CM_{\bar{z}}=M_{[\vartheta_1,\vartheta_2]}J$ for some ![]() $\vartheta_1,\vartheta_2\in L^\infty $. On the other hand, the following computation for any
$\vartheta_1,\vartheta_2\in L^\infty $. On the other hand, the following computation for any ![]() $f(=f^e\oplus f^o)\in L^2$ yields:
$f(=f^e\oplus f^o)\in L^2$ yields:
 \begin{align*}
M_{z}CM_{\bar{z}}(f) = M_{z}M_{[\psi_1,\psi_2]}JM_{\bar{z}}(f^e\oplus f^o)
=z^2\psi_2 \bar{f}^e + z^2\psi_1 \bar{f}^o
= M_{[z^2\psi_2 , z^2\psi_1 ]}J(f),
\end{align*}
\begin{align*}
M_{z}CM_{\bar{z}}(f) = M_{z}M_{[\psi_1,\psi_2]}JM_{\bar{z}}(f^e\oplus f^o)
=z^2\psi_2 \bar{f}^e + z^2\psi_1 \bar{f}^o
= M_{[z^2\psi_2 , z^2\psi_1 ]}J(f),
\end{align*} and hence  $ M_{z}CM_{\bar{z}} = M_{[z^2\psi_2 , z^2\psi_1 ]}J$. This completes the proof.
$ M_{z}CM_{\bar{z}} = M_{[z^2\psi_2 , z^2\psi_1 ]}J$. This completes the proof.
Proposition 5.3. Let C be a conjugation on L 2 intertwining ![]() $M_{z^2}$ and
$M_{z^2}$ and ![]() $M_{\bar{z}^2}$. Then
$M_{\bar{z}^2}$. Then ![]() $CJ=M_{[\psi_1,\psi_2]} $ for some
$CJ=M_{[\psi_1,\psi_2]} $ for some ![]() $\psi_1,\psi_2 \in L^\infty$ satisfying
$\psi_1,\psi_2 \in L^\infty$ satisfying ![]() $\psi_1^o= \psi_2^o$ and
$\psi_1^o= \psi_2^o$ and ![]() $|\psi_1|^2+|\psi_2|^2=2$. Furthermore, we also have
$|\psi_1|^2+|\psi_2|^2=2$. Furthermore, we also have ![]() $M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]}$.
$M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]}$.
Proof. Since ![]() $CM_{z^2}=M_{\bar{z}^2}C$, then by Corollary 4.2,
$CM_{z^2}=M_{\bar{z}^2}C$, then by Corollary 4.2, ![]() $C=M_{[\psi_1,\psi_2]}J $ for some
$C=M_{[\psi_1,\psi_2]}J $ for some ![]() $\psi_1,\psi_2 \in L^\infty$ with
$\psi_1,\psi_2 \in L^\infty$ with ![]() $\psi_1^o= \psi_2^o$ and
$\psi_1^o= \psi_2^o$ and ![]() $|\psi_1|^2+|\psi_2|^2=2$. Note that J is also a conjugation on L 2 and hence
$|\psi_1|^2+|\psi_2|^2=2$. Note that J is also a conjugation on L 2 and hence ![]() $CJ=M_{[\psi_1,\psi_2]}$. For the second part, we proceed similarly as Proposition 5.2 and obtain the following:
$CJ=M_{[\psi_1,\psi_2]}$. For the second part, we proceed similarly as Proposition 5.2 and obtain the following:
Consequently, ![]() $M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]} $. This completes the proof.
$M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]} $. This completes the proof.
Now, we are in a position to prove one of our main results related to [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10, Theorem 4.2].
Theorem 5.4. Let ![]() $\alpha, \theta $ be two non-constant inner functions and consider a
$\alpha, \theta $ be two non-constant inner functions and consider a ![]() $M_{z^2},M_{\bar{z}^2}$-intertwining conjugation C on L 2. If C satisfies the following conditions:
$M_{z^2},M_{\bar{z}^2}$-intertwining conjugation C on L 2. If C satisfies the following conditions:
(i)
 $C(K_\alpha) \subset K_\theta $ and also,
$C(K_\alpha) \subset K_\theta $ and also,  $M_zCM_z(K_\alpha) \subset K_\theta $,
$M_zCM_z(K_\alpha) \subset K_\theta $,(ii)
 $Re[(M_{z}CJM_{\bar{z}})^*(CJ)] =I$,
$Re[(M_{z}CJM_{\bar{z}})^*(CJ)] =I$,
then there exists an inner function γ such that ![]() $C+M_zCM_z = \sqrt{2}\mathscr{C}_\gamma$, where γ is divisible by α and γ divides θ, in other words,
$C+M_zCM_z = \sqrt{2}\mathscr{C}_\gamma$, where γ is divisible by α and γ divides θ, in other words, ![]() $\alpha \leq \gamma \leq \theta$.
$\alpha \leq \gamma \leq \theta$.
Proof. Since ![]() $CM_{z^2}=M_{\bar{z}^2}C$, then by Proposition 5.3 ,
$CM_{z^2}=M_{\bar{z}^2}C$, then by Proposition 5.3 , ![]() $C=M_{[\psi_1,\psi_2]}J$ and
$C=M_{[\psi_1,\psi_2]}J$ and ![]() $M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]} $ for some
$M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]} $ for some ![]() $\psi_1,\psi_2 \in L^\infty$ satisfying
$\psi_1,\psi_2 \in L^\infty$ satisfying ![]() $\psi_1^o= \psi_2^o$ and
$\psi_1^o= \psi_2^o$ and ![]() $|\psi_1|^2+|\psi_2|^2=2$. Next, we consider the reproducing kernel function at 0, that is
$|\psi_1|^2+|\psi_2|^2=2$. Next, we consider the reproducing kernel function at 0, that is ![]() $k^\alpha_0= 1-\overline{\alpha(0)}\alpha$ and its conjugate
$k^\alpha_0= 1-\overline{\alpha(0)}\alpha$ and its conjugate  $\tilde{k}^\alpha_0 =\mathscr{C}_\alpha k^\alpha_0 =\bar{z}( \alpha -\alpha(0))$ in Kα. Therefore by simple calculations, we get
$\tilde{k}^\alpha_0 =\mathscr{C}_\alpha k^\alpha_0 =\bar{z}( \alpha -\alpha(0))$ in Kα. Therefore by simple calculations, we get
 \begin{align*}
C(\tilde{k}^\alpha_0) = M_{[\psi_1,\psi_2]}J(\bar{z}( \alpha -\alpha(0)))
= M_{[\psi_1,\psi_2]}(zf^e+zf^o)
= \psi_1 zf^o + \psi_2 zf^e,
\end{align*}
\begin{align*}
C(\tilde{k}^\alpha_0) = M_{[\psi_1,\psi_2]}J(\bar{z}( \alpha -\alpha(0)))
= M_{[\psi_1,\psi_2]}(zf^e+zf^o)
= \psi_1 zf^o + \psi_2 zf^e,
\end{align*} where ![]() $f=\overline{(\alpha -\alpha(0))} $. Similarly, we also have,
$f=\overline{(\alpha -\alpha(0))} $. Similarly, we also have,
 \begin{align*}
M_z C M_z(\tilde{k}^\alpha_0) = M_z M_{[\psi_1,\psi_2]}J( \alpha -\alpha(0))
= M_z M_{[\psi_1,\psi_2]}\overline{(\alpha -\alpha(0))}
= \psi_1 zf^e + \psi_2 zf^o.
\end{align*}
\begin{align*}
M_z C M_z(\tilde{k}^\alpha_0) = M_z M_{[\psi_1,\psi_2]}J( \alpha -\alpha(0))
= M_z M_{[\psi_1,\psi_2]}\overline{(\alpha -\alpha(0))}
= \psi_1 zf^e + \psi_2 zf^o.
\end{align*} Since  $C(\tilde{k}^\alpha_0),M_zCM_z(\tilde{k}^\alpha_0) \in K_\theta $, then
$C(\tilde{k}^\alpha_0),M_zCM_z(\tilde{k}^\alpha_0) \in K_\theta $, then  $C(\tilde{k}^\alpha_0)+M_zCM_z(\tilde{k}^\alpha_0)\in K_\theta$. In other words,
$C(\tilde{k}^\alpha_0)+M_zCM_z(\tilde{k}^\alpha_0)\in K_\theta$. In other words, ![]() $(\psi_1 +\psi_2)zf \in K_\theta $ which implies that there exist
$(\psi_1 +\psi_2)zf \in K_\theta $ which implies that there exist ![]() $g\in K_\theta $ such that
$g\in K_\theta $ such that ![]() $g=(\psi_1 +\psi_2)z\overline{(\alpha -\alpha(0))}=(\psi_1 +\psi_2)z\bar{\alpha} (1-\bar{\alpha}(0)\alpha )$. Note that
$g=(\psi_1 +\psi_2)z\overline{(\alpha -\alpha(0))}=(\psi_1 +\psi_2)z\bar{\alpha} (1-\bar{\alpha}(0)\alpha )$. Note that ![]() $(1-\overline{\alpha(0)}\alpha)^{-1}$ is a bounded analytic function and hence,
$(1-\overline{\alpha(0)}\alpha)^{-1}$ is a bounded analytic function and hence,
which yields ![]() $z(\psi_1+\psi_2)\in H^\infty$. Our next aim is to show that
$z(\psi_1+\psi_2)\in H^\infty$. Our next aim is to show that  $\dfrac{z(\psi_1+\psi_2)}{2}=\gamma(say)$ is an inner function. Since
$\dfrac{z(\psi_1+\psi_2)}{2}=\gamma(say)$ is an inner function. Since ![]() $CJ=M_{[\psi_1,\psi_2]}$ and
$CJ=M_{[\psi_1,\psi_2]}$ and ![]() $M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]} $, then it follows that:
$M_{z}CJM_{\bar{z}}=M_{[\psi_2,\psi_1]} $, then it follows that:
 \begin{equation*}(M_{z}CJM_{\bar{z}})^*(CJ) = M_{[\psi_2,\psi_1]}^*M_{[\psi_1,\psi_2]}.\end{equation*}
\begin{equation*}(M_{z}CJM_{\bar{z}})^*(CJ) = M_{[\psi_2,\psi_1]}^*M_{[\psi_1,\psi_2]}.\end{equation*} By considering the decomposition ![]() $L^2(\mathbb{T})=\mathcal{H}_1(1,z^2) \oplus \mathcal{H}_2(z,z^2)$, we have the following block-matrix representation:
$L^2(\mathbb{T})=\mathcal{H}_1(1,z^2) \oplus \mathcal{H}_2(z,z^2)$, we have the following block-matrix representation:
 \begin{align*}
M_{[\psi_2,\psi_1]}^*M_{[\psi_1,\psi_2]} &=
\begin{bmatrix}
M_{\bar{\psi_2^e}\psi_1^e+\bar{\psi_2^o}\psi_1^o}&& M_{\bar{\psi_2^e}\psi_2^o+\bar{\psi_2^o}\psi_2^e}\\
\\
M_{\bar{\psi_1^o}\psi_1^e+\bar{\psi_1^e}\psi_1^o} && M_{\bar{\psi_1^o}\psi_2^o+\bar{\psi_1^e}\psi_2^e}\\
\end{bmatrix}.
\end{align*}
\begin{align*}
M_{[\psi_2,\psi_1]}^*M_{[\psi_1,\psi_2]} &=
\begin{bmatrix}
M_{\bar{\psi_2^e}\psi_1^e+\bar{\psi_2^o}\psi_1^o}&& M_{\bar{\psi_2^e}\psi_2^o+\bar{\psi_2^o}\psi_2^e}\\
\\
M_{\bar{\psi_1^o}\psi_1^e+\bar{\psi_1^e}\psi_1^o} && M_{\bar{\psi_1^o}\psi_2^o+\bar{\psi_1^e}\psi_2^e}\\
\end{bmatrix}.
\end{align*} Therefore, the condition ![]() $Re[(M_{z}CJM_{\bar{z}})^*(CJ)] =I$ boils down to
$Re[(M_{z}CJM_{\bar{z}})^*(CJ)] =I$ boils down to  $ Re\left[M_{[\psi_2,\psi_1]}^*M_{[\psi_1,\psi_2]}\right]=I$ which produces the following two conditions:
$ Re\left[M_{[\psi_2,\psi_1]}^*M_{[\psi_1,\psi_2]}\right]=I$ which produces the following two conditions:
 \begin{equation}
\begin{cases}
& Re[\bar{\psi_2^e}\psi_1^e+\bar{\psi_2^o}\psi_1^o] =1, \\
& \bar{\psi_2^e}\psi_2^o+\bar{\psi_2^o}\psi_2^e + \psi_1^o\bar{\psi_1^e}+\psi_1^e\bar{\psi_1^o}=0.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
& Re[\bar{\psi_2^e}\psi_1^e+\bar{\psi_2^o}\psi_1^o] =1, \\
& \bar{\psi_2^e}\psi_2^o+\bar{\psi_2^o}\psi_2^e + \psi_1^o\bar{\psi_1^e}+\psi_1^e\bar{\psi_1^o}=0.
\end{cases}
\end{equation} Recall that, to characterize the class of conjugations C intertwining ![]() $M_{z^2}$ and
$M_{z^2}$ and ![]() $M_{\bar{z}^2}$, we initially obtain the conditions (4.4) in Remark 4.3. Therefore, combining the conditions (5.1) and
$M_{\bar{z}^2}$, we initially obtain the conditions (4.4) in Remark 4.3. Therefore, combining the conditions (5.1) and ![]() $\bar{\psi_2^o}\psi_1^e+\bar{\psi_2^e}\psi_1^o=0$ in (4.4), we get,
$\bar{\psi_2^o}\psi_1^e+\bar{\psi_2^e}\psi_1^o=0$ in (4.4), we get,
Thus, ![]() $|\psi_1+\psi_2|^2=|\psi_1|^2+|\psi_2|^2+2Re[\psi_2\bar{\psi_1]}=4$, and hence
$|\psi_1+\psi_2|^2=|\psi_1|^2+|\psi_2|^2+2Re[\psi_2\bar{\psi_1]}=4$, and hence  $|\gamma|=|\dfrac{z(\psi_1+\psi_2)}{2}|=1$ a.e. on
$|\gamma|=|\dfrac{z(\psi_1+\psi_2)}{2}|=1$ a.e. on ![]() $\mathbb{T}$. Therefore,
$\mathbb{T}$. Therefore, ![]() $\bar{\alpha}\gamma\in H^2$ shows that γ is divisible by α. Moreover, we also obtain,
$\bar{\alpha}\gamma\in H^2$ shows that γ is divisible by α. Moreover, we also obtain,
 \begin{align*}
\mathscr{C}_\theta (C+M_zCM_z)(k^\alpha_0) & = \mathscr{C}_\theta (M_{[\psi_1,\psi_2]}J+M_zM_{[\psi_1,\psi_2]}JM_z)(1-\overline{\alpha(0)}\alpha)\\
& = \theta \overline{z(\psi_1+\psi_2)}(1-\overline{\alpha(0)}\alpha)\in K_\theta.
\end{align*}
\begin{align*}
\mathscr{C}_\theta (C+M_zCM_z)(k^\alpha_0) & = \mathscr{C}_\theta (M_{[\psi_1,\psi_2]}J+M_zM_{[\psi_1,\psi_2]}JM_z)(1-\overline{\alpha(0)}\alpha)\\
& = \theta \overline{z(\psi_1+\psi_2)}(1-\overline{\alpha(0)}\alpha)\in K_\theta.
\end{align*} Therefore, ![]() $\theta \bar{\gamma} \in H^2$ implies that θ is divisible by γ. Moreover, one can easily conclude that
$\theta \bar{\gamma} \in H^2$ implies that θ is divisible by γ. Moreover, one can easily conclude that ![]() $C+M_zCM_z=2\mathscr{C}_\gamma$.
$C+M_zCM_z=2\mathscr{C}_\gamma$.
Next, we discuss the relationship between ![]() $only~M_{z^2}-commuting$ conjugations and model spaces. Before we start, recall some useful facts obtained in [Reference Cima, Garcia, Ross and Wogen4] as follows:
$only~M_{z^2}-commuting$ conjugations and model spaces. Before we start, recall some useful facts obtained in [Reference Cima, Garcia, Ross and Wogen4] as follows:
 \begin{equation}
J^\star(K_\alpha)=K_{\alpha^\#},~
J^\star \mathscr{C}_\alpha = \mathscr{C}_{\alpha^\#}J^\star,~\quad \text{and} \quad
J^\star(\alpha H^2) = \alpha^\# H^2.
\end{equation}
\begin{equation}
J^\star(K_\alpha)=K_{\alpha^\#},~
J^\star \mathscr{C}_\alpha = \mathscr{C}_{\alpha^\#}J^\star,~\quad \text{and} \quad
J^\star(\alpha H^2) = \alpha^\# H^2.
\end{equation} Note that, for an antilinear operator T, ![]() $T^\sharp$ denotes the antilinear adjoint of T.
$T^\sharp$ denotes the antilinear adjoint of T.
Theorem 5.5. Let ![]() $\alpha, \theta $ be two non-constant inner functions and let C be a
$\alpha, \theta $ be two non-constant inner functions and let C be a ![]() $only~M_{z^2}-commuting$ conjugation C on L 2. If C satisfies the following conditions:
$only~M_{z^2}-commuting$ conjugation C on L 2. If C satisfies the following conditions:
(i)
 $J^\star C$ is
$J^\star C$ is  $\mathscr{C}_\alpha $-symmetric,
$\mathscr{C}_\alpha $-symmetric,(ii)
 $C(K_\alpha) \subset K_\theta $ and
$C(K_\alpha) \subset K_\theta $ and  $M_zCM_{\bar{z}}(K_\alpha) \subset K_\theta $,
$M_zCM_{\bar{z}}(K_\alpha) \subset K_\theta $,(iii)
 $Re\left[(M_{z}C\mathscr{C}_\alpha JM_{\bar{z}})^\sharp(C\mathscr{C}_\alpha J)\right] =I$,
$Re\left[(M_{z}C\mathscr{C}_\alpha JM_{\bar{z}})^\sharp(C\mathscr{C}_\alpha J)\right] =I$,
then there exists an inner function ψ satisfying ![]() $\alpha \leq \psi \leq \theta^\#$ such that
$\alpha \leq \psi \leq \theta^\#$ such that  $C+M_zCM_{\bar{z}} = J^\star M_{\frac{2\psi}{\alpha}}$.
$C+M_zCM_{\bar{z}} = J^\star M_{\frac{2\psi}{\alpha}}$.
Proof. Since C is a ![]() $only~M_{z^2}-commuting$ conjugation, then by Corollary 4.7, there exist
$only~M_{z^2}-commuting$ conjugation, then by Corollary 4.7, there exist ![]() $\xi_1,\xi_2\in L^\infty$ such that
$\xi_1,\xi_2\in L^\infty$ such that ![]() $C=M_{[\xi_1,\xi_2]}J^\star$ and
$C=M_{[\xi_1,\xi_2]}J^\star$ and ![]() $\xi_1,\xi_2$ satisfy
$\xi_1,\xi_2$ satisfy ![]() $|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z)$. Note that
$|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z)$. Note that  $J^\star C=M_{[\xi_1,\xi_2]}^*$ and by hypothesis, it is
$J^\star C=M_{[\xi_1,\xi_2]}^*$ and by hypothesis, it is ![]() $\mathscr{C}_\alpha$-symmetric. Next, we consider the antilinear operator
$\mathscr{C}_\alpha$-symmetric. Next, we consider the antilinear operator ![]() $J^\star C \mathscr{C}_\alpha $ on L 2, and we have the following observations:
$J^\star C \mathscr{C}_\alpha $ on L 2, and we have the following observations:
(i)
 $(J^\star C \mathscr{C}_\alpha)^2 =J^\star C \mathscr{C}_\alpha J^\star C \mathscr{C}_\alpha =M_{[\xi_1,\xi_2]}^*\mathscr{C}_\alpha M_{[\xi_1,\xi_2]}^*\mathscr{C}_\alpha=M_{[\xi_1,\xi_2]}^*M_{[\xi_1,\xi_2]}=I$,
$(J^\star C \mathscr{C}_\alpha)^2 =J^\star C \mathscr{C}_\alpha J^\star C \mathscr{C}_\alpha =M_{[\xi_1,\xi_2]}^*\mathscr{C}_\alpha M_{[\xi_1,\xi_2]}^*\mathscr{C}_\alpha=M_{[\xi_1,\xi_2]}^*M_{[\xi_1,\xi_2]}=I$,(ii)
 $\langle J^\star C \mathscr{C}_\alpha(f),J^\star C \mathscr{C}_\alpha(g)\rangle =\langle g,f\rangle $ for any
$\langle J^\star C \mathscr{C}_\alpha(f),J^\star C \mathscr{C}_\alpha(g)\rangle =\langle g,f\rangle $ for any  $f,g \in L^2$.
$f,g \in L^2$.
Therefore, ![]() $J^\star C \mathscr{C}_\alpha $ is a conjugation satisfying
$J^\star C \mathscr{C}_\alpha $ is a conjugation satisfying ![]() $J^\star C \mathscr{C}_\alpha M_{z^2} = M_{\bar{z}^2} J^\star C \mathscr{C}_\alpha $, but observe that
$J^\star C \mathscr{C}_\alpha M_{z^2} = M_{\bar{z}^2} J^\star C \mathscr{C}_\alpha $, but observe that ![]() $J^\star C \mathscr{C}_\alpha M_z \neq M_{\bar{z}}J^\star C \mathscr{C}_\alpha$. Moreover, using the hypothesis, we get:
$J^\star C \mathscr{C}_\alpha M_z \neq M_{\bar{z}}J^\star C \mathscr{C}_\alpha$. Moreover, using the hypothesis, we get:
and ![]() $M_zJ^\star C \mathscr{C}_\alpha M_z(K_\alpha)=J^\star M_zC M_{\bar{z}}\mathscr{C}_\alpha (K_\alpha)=J^\star M_zC M_{\bar{z}}(K_\alpha)\subset J^\star(K_\theta)=K_{\theta^{\#}} $. Furthermore,
$M_zJ^\star C \mathscr{C}_\alpha M_z(K_\alpha)=J^\star M_zC M_{\bar{z}}\mathscr{C}_\alpha (K_\alpha)=J^\star M_zC M_{\bar{z}}(K_\alpha)\subset J^\star(K_\theta)=K_{\theta^{\#}} $. Furthermore,
Finally, by applying Theorem 5.4 and using the fact ![]() $\mathscr{C}_\alpha M_z=M_{\bar{z}}\mathscr{C}_\alpha$ , there exists an inner function ψ satisfying
$\mathscr{C}_\alpha M_z=M_{\bar{z}}\mathscr{C}_\alpha$ , there exists an inner function ψ satisfying ![]() $\alpha \leq \psi \leq \theta ^{\#}$ such that:
$\alpha \leq \psi \leq \theta ^{\#}$ such that:
 \begin{align*}
& J^\star C \mathscr{C}_\alpha +M_z J^\star C \mathscr{C}_\alpha M_z =2\mathscr{C}_\psi
\implies J^\star C \mathscr{C}_\alpha + J^\star M_z C M_{\bar{z}}\mathscr{C}_\alpha = 2\mathscr{C}_\psi \\
& \implies C + M_z C M_{\bar{z}} =J^\star 2\mathscr{C}_\psi \mathscr{C}_\alpha
\implies C + M_z C M_{\bar{z}} = J^\star M_{\frac{2\psi}{\alpha}}.
\end{align*}
\begin{align*}
& J^\star C \mathscr{C}_\alpha +M_z J^\star C \mathscr{C}_\alpha M_z =2\mathscr{C}_\psi
\implies J^\star C \mathscr{C}_\alpha + J^\star M_z C M_{\bar{z}}\mathscr{C}_\alpha = 2\mathscr{C}_\psi \\
& \implies C + M_z C M_{\bar{z}} =J^\star 2\mathscr{C}_\psi \mathscr{C}_\alpha
\implies C + M_z C M_{\bar{z}} = J^\star M_{\frac{2\psi}{\alpha}}.
\end{align*}This completes the proof.
It is important to note that assumptions made in Theorem 5.4 and Theorem 5.5 above are fully consistent with the assumptions made in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10, Theorem 4.2] and [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10, Theorem 4.6], respectively.
5.3. S-invariant subspaces preserving conjugations
In this subsection, we characterize all conjugations C preserving shift invariant subspaces and intertwining ![]() $M_{z^2}$,
$M_{z^2}$, ![]() $M_{\bar{z}^2}$. Moreover, we also characterize all
$M_{\bar{z}^2}$. Moreover, we also characterize all ![]() $M_{z^2}$-commuting conjugations C that preserve shift-invariant subspaces.
$M_{z^2}$-commuting conjugations C that preserve shift-invariant subspaces.
Theorem 5.6. There exist no ![]() $M_{z^2}$ and
$M_{z^2}$ and ![]() $M_{\bar{z}^2}$ intertwining conjugations in L 2 that map any Beurling type subspace
$M_{\bar{z}^2}$ intertwining conjugations in L 2 that map any Beurling type subspace ![]() $\alpha H^2$ into another
$\alpha H^2$ into another ![]() $\theta H^2$ for any two inner functions α and θ.
$\theta H^2$ for any two inner functions α and θ.
Proof. Let C be a ![]() $M_{z^2},M_{\bar{z}^2}$-intertwining conjugation on L 2 such that
$M_{z^2},M_{\bar{z}^2}$-intertwining conjugation on L 2 such that ![]() $C(\alpha H^2)\subset \theta H^2$. Since C satisfies
$C(\alpha H^2)\subset \theta H^2$. Since C satisfies ![]() $CM_{z^2}=M_{\bar{z}^2}C$, then by Corollary (4.2), there exist
$CM_{z^2}=M_{\bar{z}^2}C$, then by Corollary (4.2), there exist ![]() $\psi_1,\psi_2 \in L^\infty$ such that
$\psi_1,\psi_2 \in L^\infty$ such that ![]() $C=M_{[\psi_1,\psi_2]}J$ and
$C=M_{[\psi_1,\psi_2]}J$ and ![]() $\psi_1^o= \psi_2^o$,
$\psi_1^o= \psi_2^o$, ![]() $|\psi_1|^2+|\psi_2|^2=2$. Since
$|\psi_1|^2+|\psi_2|^2=2$. Since ![]() $C(\alpha H^2)\subset \theta H^2$, then there exists
$C(\alpha H^2)\subset \theta H^2$, then there exists ![]() $f\in H^2$ such that:
$f\in H^2$ such that:
Similarly, for ![]() $n=2k,k\geq 0$, we get,
$n=2k,k\geq 0$, we get,
for some ![]() $h_n\in H^2$ and hence
$h_n\in H^2$ and hence ![]() $\bar{z}^n f = h _n
\in H^2$. Thus for any non-negative even integer n,
$\bar{z}^n f = h _n
\in H^2$. Thus for any non-negative even integer n,
Similarly, ![]() $\langle \bar{z}^nf, \bar{z}^2 \rangle =0$ implies
$\langle \bar{z}^nf, \bar{z}^2 \rangle =0$ implies ![]() $f^e =0$ and hence we conclude that f = 0. Thus
$f^e =0$ and hence we conclude that f = 0. Thus ![]() $C(\alpha)=0$, a contradiction.
$C(\alpha)=0$, a contradiction.
Now, we move to the characterization of ![]() $M_{z^2}$-commuting conjugations that map a shift-invariant subspace
$M_{z^2}$-commuting conjugations that map a shift-invariant subspace ![]() $\alpha H^2$ into another one, say
$\alpha H^2$ into another one, say ![]() $\theta H^2$.
$\theta H^2$.
Theorem 5.7. Let α and β be two inner functions, and let C be any ![]() $M_{z^2}$-commuting conjugation on L 2 satisfying
$M_{z^2}$-commuting conjugation on L 2 satisfying ![]() $Re[(M_{\bar
z}CJ^\star M_z)^*(CJ^\star)]=I$. If
$Re[(M_{\bar
z}CJ^\star M_z)^*(CJ^\star)]=I$. If ![]() $C(\alpha H^2)\subset \beta H^2$, then
$C(\alpha H^2)\subset \beta H^2$, then ![]() $\beta \beta^\# \leq \alpha \alpha^\#$ and
$\beta \beta^\# \leq \alpha \alpha^\#$ and ![]() $C+M_zCM_z =2\mathscr{C}_{\theta}J^*\mathscr{C}_{\alpha}$, where θ is an inner function such that
$C+M_zCM_z =2\mathscr{C}_{\theta}J^*\mathscr{C}_{\alpha}$, where θ is an inner function such that ![]() $\beta \leq \theta$,
$\beta \leq \theta$, ![]() $\theta \theta ^\# =\alpha \alpha^\#$ and
$\theta \theta ^\# =\alpha \alpha^\#$ and ![]() $\theta\overline{\alpha ^\#}$ is symmetric.
$\theta\overline{\alpha ^\#}$ is symmetric.
Proof. Since ![]() $CM_{z^2}=M_{z^2}C$, then by Corollary (4.2), there exist
$CM_{z^2}=M_{z^2}C$, then by Corollary (4.2), there exist ![]() $\xi_1,\xi_2\in L^\infty$ such that
$\xi_1,\xi_2\in L^\infty$ such that ![]() $C=M_{[\xi_1,\xi_2]}J^\star$ and
$C=M_{[\xi_1,\xi_2]}J^\star$ and ![]() $|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z)$. Now, by using the condition
$|\xi_1|^2+|\xi_2|^2=2,|\xi_2^e+\xi_1^o|^2+| \xi_2^o+\xi_1^e|^2=2,\xi_1^o(\bar{z})=\xi_2^o(z), \xi_1^e(\bar{z})=\xi_1^e(z), \xi_2^e(\bar{z})=\xi_2^e(z)$. Now, by using the condition ![]() $C(\alpha H^2)\subset \beta H^2$, we conclude that
$C(\alpha H^2)\subset \beta H^2$, we conclude that
 \begin{equation*}C(\alpha)=M_{[\xi_1,\xi_2]}J^\star (\alpha) = \xi_1 {\alpha^e}^{\#} +\xi_2 {\alpha^o}^{\#} \in \beta H^2.\end{equation*}
\begin{equation*}C(\alpha)=M_{[\xi_1,\xi_2]}J^\star (\alpha) = \xi_1 {\alpha^e}^{\#} +\xi_2 {\alpha^o}^{\#} \in \beta H^2.\end{equation*} Moreover, we also have ![]() $M_z C M_z (\alpha H^2)\subset M_zC(\alpha)\subset M_z(\beta H^2)\subset \beta H^2$. Similarly,
$M_z C M_z (\alpha H^2)\subset M_zC(\alpha)\subset M_z(\beta H^2)\subset \beta H^2$. Similarly,
 \begin{equation*}M_zCM_z(\alpha )= \xi_1 {\alpha^o}^{\#} +\xi_2 {\alpha^e}^{\#} \in \beta H^2.\end{equation*}
\begin{equation*}M_zCM_z(\alpha )= \xi_1 {\alpha^o}^{\#} +\xi_2 {\alpha^e}^{\#} \in \beta H^2.\end{equation*} Therefore, ![]() $\xi_1 {\alpha^e}^{\#} +\xi_2 {\alpha^o}^{\#} + \xi_1 {\alpha^o}^{\#} +\xi_2 {\alpha^e}^{\#} \in \beta H^2$ implies that there exists
$\xi_1 {\alpha^e}^{\#} +\xi_2 {\alpha^o}^{\#} + \xi_1 {\alpha^o}^{\#} +\xi_2 {\alpha^e}^{\#} \in \beta H^2$ implies that there exists ![]() $h\in H^2$ such that:
$h\in H^2$ such that:
On the other hand, ![]() $CJ^\star = M_{[\xi_1,\xi_2]}$ and
$CJ^\star = M_{[\xi_1,\xi_2]}$ and ![]() $M_{\bar
z} CJ^\star M_z = M_{[\xi_2,\xi_1]}$, and hence
$M_{\bar
z} CJ^\star M_z = M_{[\xi_2,\xi_1]}$, and hence ![]() $Re\left[(M_{\bar
z}CJ^\star M_z)^*(CJ^\star)\right]=I$, which yields the following conditions:
$Re\left[(M_{\bar
z}CJ^\star M_z)^*(CJ^\star)\right]=I$, which yields the following conditions:
 \begin{equation}
\begin{cases}
& Re\left[\bar{\xi_2^e}\xi_1^e+\bar{\xi_2^o}\xi_1^o\right] =1 , \\
& \bar{\xi_2^e}\xi_2^o+\bar{\xi_2^o}\xi_2^e + \xi_1^o\bar{\xi_1^e}+\xi_1^e\bar{\xi_1^o}=0.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
& Re\left[\bar{\xi_2^e}\xi_1^e+\bar{\xi_2^o}\xi_1^o\right] =1 , \\
& \bar{\xi_2^e}\xi_2^o+\bar{\xi_2^o}\xi_2^e + \xi_1^o\bar{\xi_1^e}+\xi_1^e\bar{\xi_1^o}=0.
\end{cases}
\end{equation}Next, by combining conditions obtained in (5.4) and (4.11), we conclude:
and hence ![]() $|\xi_1+\xi_2|^2=|\xi_1|^2 +|\xi_2|^2+ 2Re[\xi_2\bar{\xi_1}]=4$. Suppose
$|\xi_1+\xi_2|^2=|\xi_1|^2 +|\xi_2|^2+ 2Re[\xi_2\bar{\xi_1}]=4$. Suppose  $\psi = \dfrac{\xi_1 + \xi_2}{2}$, then
$\psi = \dfrac{\xi_1 + \xi_2}{2}$, then ![]() $|\psi|=1$. Therefore, from (5.3) we get
$|\psi|=1$. Therefore, from (5.3) we get ![]() $\psi\alpha^{\#} = \beta f$ for some
$\psi\alpha^{\#} = \beta f$ for some ![]() $f\in H^2$. On the other hand, ψ is a symmetric function since
$f\in H^2$. On the other hand, ψ is a symmetric function since  $\psi(\bar{z})=\frac{1}{2}[\xi_1(\bar{z})+\xi_2(\bar{z})]= \frac{1}{2}[(\xi_1^e(\bar{z})+\xi_1^o(\bar{z})+(\xi_2^e(\bar{z})+\xi_2^o(\bar{z})]=\frac{1}{2}[(\xi_1^e(z)+\xi_2^o(z)) + (\xi_2^e(z)+\xi_1^o(z))]= \frac{1}{2}[(\xi_1+\xi_2)(z)]=\psi(z)$. Let
$\psi(\bar{z})=\frac{1}{2}[\xi_1(\bar{z})+\xi_2(\bar{z})]= \frac{1}{2}[(\xi_1^e(\bar{z})+\xi_1^o(\bar{z})+(\xi_2^e(\bar{z})+\xi_2^o(\bar{z})]=\frac{1}{2}[(\xi_1^e(z)+\xi_2^o(z)) + (\xi_2^e(z)+\xi_1^o(z))]= \frac{1}{2}[(\xi_1+\xi_2)(z)]=\psi(z)$. Let ![]() $\theta = \beta f$, then
$\theta = \beta f$, then ![]() $\theta \overline{\alpha^{\#}}=\psi$ is symmetric. Moreover, θ is an inner function such that
$\theta \overline{\alpha^{\#}}=\psi$ is symmetric. Moreover, θ is an inner function such that ![]() $\beta \leq \theta$ and
$\beta \leq \theta$ and ![]() $\theta \theta^{\#}=\alpha \alpha^{\#}$ which immediately implies
$\theta \theta^{\#}=\alpha \alpha^{\#}$ which immediately implies ![]() $\beta \beta ^{\#} \leq \alpha \alpha^\#$. Furthermore, by simple calculations, one can also obtain the following identity:
$\beta \beta ^{\#} \leq \alpha \alpha^\#$. Furthermore, by simple calculations, one can also obtain the following identity:
This completes the proof.
Remark 5.8. Note that the converse of Theorem 5.7 may not be true in general. In other words, for the converse, if we assume ![]() $\beta \beta ^{\#} \leq \alpha \alpha^\#$, then by mimicking the proof of Theorem 5.2 in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10], one can show that
$\beta \beta ^{\#} \leq \alpha \alpha^\#$, then by mimicking the proof of Theorem 5.2 in [Reference Câmara, Kliś-Garlicka, Łanucha and Ptak10], one can show that ![]() $C+M_zCM_z =2\mathscr{C}_\theta J^* \mathscr{C}_\alpha$, which maps
$C+M_zCM_z =2\mathscr{C}_\theta J^* \mathscr{C}_\alpha$, which maps ![]() $\alpha H^2$ onto
$\alpha H^2$ onto ![]() $\theta H^2 \subset \beta H^2$ but not necessarily
$\theta H^2 \subset \beta H^2$ but not necessarily ![]() $C(\alpha H^2) \subset \beta H^2$.
$C(\alpha H^2) \subset \beta H^2$.
6. Conjugations related to MB
In this section, we want to investigate some of the earlier characterization results in the context of MB, where B is a finite Blaschke product. Let B be a finite Blaschke product of degree (or order, say) n, then the dimension of the model space ![]() $K_B:=H^2\ominus BH^2$ is n. Let
$K_B:=H^2\ominus BH^2$ is n. Let ![]() $\{e_1,e_2,\ldots e_n\}$ be an orthonormal basis of KB. Recall that (see
$\{e_1,e_2,\ldots e_n\}$ be an orthonormal basis of KB. Recall that (see ![]() $\S$ 3, (2.2)),
$\S$ 3, (2.2)),
For example, if ![]() $B(z)=z^2$, then for any
$B(z)=z^2$, then for any ![]() $f\in L^2(\mathbb{T})$, we have
$f\in L^2(\mathbb{T})$, we have ![]() $f=f^e\oplus f^o$, where
$f=f^e\oplus f^o$, where  $f^e \in \bigvee\limits_{k=-\infty}^{\infty}\{z^{2k}\} =\mathcal{H}_1(1,z^2)$ and
$f^e \in \bigvee\limits_{k=-\infty}^{\infty}\{z^{2k}\} =\mathcal{H}_1(1,z^2)$ and  $f^o \in \bigvee\limits_{k=-\infty}^{\infty}\{z^{2k+1}\}=\mathcal{H}_1(z,z^2)$, and we are already familiar with such factorization in earlier sections. Now if
$f^o \in \bigvee\limits_{k=-\infty}^{\infty}\{z^{2k+1}\}=\mathcal{H}_1(z,z^2)$, and we are already familiar with such factorization in earlier sections. Now if ![]() $B(z)=z^n$, then for any
$B(z)=z^n$, then for any  $f(z)=\sum\limits_{k=-\infty}^{\infty}a_kz^k \in L^2(\mathbb{T})$ has the following decomposition:
$f(z)=\sum\limits_{k=-\infty}^{\infty}a_kz^k \in L^2(\mathbb{T})$ has the following decomposition:
 \begin{equation}
f(z) = \sum_{k=-\infty}^{\infty}a_{nk}z^{nk} +\sum_{k=-\infty}^{\infty}a_{nk+1}z^{nk+1}+\cdots +\sum_{k=-\infty}^{\infty}a_{nk+n-1}z^{nk+n-1},
\end{equation}
\begin{equation}
f(z) = \sum_{k=-\infty}^{\infty}a_{nk}z^{nk} +\sum_{k=-\infty}^{\infty}a_{nk+1}z^{nk+1}+\cdots +\sum_{k=-\infty}^{\infty}a_{nk+n-1}z^{nk+n-1},
\end{equation} where  $f_i(z)=\sum\limits_{k=-\infty}^{\infty}a_{nk+i-1}z^{nk+i-1}\in \mathcal{H}_i(z^i,z^n)$ for
$f_i(z)=\sum\limits_{k=-\infty}^{\infty}a_{nk+i-1}z^{nk+i-1}\in \mathcal{H}_i(z^i,z^n)$ for ![]() $i\in\{0,1,\ldots ,n-1\}$. Recall the following two well-known facts:
$i\in\{0,1,\ldots ,n-1\}$. Recall the following two well-known facts:
The following theorem is one of the main results in this section, which generalize Theorem 4.1 and Theorem 4.5 of ![]() $\S$ 4.
$\S$ 4.
Theorem 6.1. Let ![]() $C:L^2(\mathbb{T}) \to L^2(\mathbb{T})$ be a conjugation.
$C:L^2(\mathbb{T}) \to L^2(\mathbb{T})$ be a conjugation.
(i) If
 $CM_B = M_{\bar{B}}C$, then there exist
$CM_B = M_{\bar{B}}C$, then there exist  $\phi_1,\phi_2,\ldots ,\phi_n \in L^{\infty}$ such that
$\phi_1,\phi_2,\ldots ,\phi_n \in L^{\infty}$ such that  $C=M_{[\phi_1,\phi_2,\ldots ,\phi_n]} \mathscr{C}_B $, where
$C=M_{[\phi_1,\phi_2,\ldots ,\phi_n]} \mathscr{C}_B $, where  $M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ is unitary and
$M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ is unitary and  $\mathscr{C}_B$-symmetric.
$\mathscr{C}_B$-symmetric.(ii) If
 $CM_{B} =M_BC$, then there exist
$CM_{B} =M_BC$, then there exist  $\psi_1,\psi_2,\ldots ,\psi_n \in L^{\infty}$ such that
$\psi_1,\psi_2,\ldots ,\psi_n \in L^{\infty}$ such that  $C=M_{[\psi_1,\psi_2,\ldots ,\psi_n]} \mathscr{C}_B^\star $, where
$C=M_{[\psi_1,\psi_2,\ldots ,\psi_n]} \mathscr{C}_B^\star $, where  $M_{[\psi_1,\psi_2,\ldots ,\psi_n]}$ is unitary and
$M_{[\psi_1,\psi_2,\ldots ,\psi_n]}$ is unitary and  $\mathscr{C}_B^\star$-symmetric.
$\mathscr{C}_B^\star$-symmetric.
(i) Let
 $C:L^2(\mathbb{T}) \to L^2(\mathbb{T})$ be a conjugation such that
$C:L^2(\mathbb{T}) \to L^2(\mathbb{T})$ be a conjugation such that  $CM_B = M_{\bar{B}}C$, then using (6.2), we conclude that
$CM_B = M_{\bar{B}}C$, then using (6.2), we conclude that  $C\circ \mathscr{C}_B$ is a unitary operator on L 2 satisfying
$C\circ \mathscr{C}_B$ is a unitary operator on L 2 satisfying  $C\circ \mathscr{C}_B M_B =M_B C\circ \mathscr{C}_B$. Therefore, from Theorem 2.2, we get
$C\circ \mathscr{C}_B M_B =M_B C\circ \mathscr{C}_B$. Therefore, from Theorem 2.2, we get  $\phi_1, \phi_2, \ldots, \phi_n\in L^\infty$ such that
$\phi_1, \phi_2, \ldots, \phi_n\in L^\infty$ such that  $C\circ \mathscr{C}_B = M_{[\phi_1,\phi_2,\cdots ,\phi_n]}$, and hence
$C\circ \mathscr{C}_B = M_{[\phi_1,\phi_2,\cdots ,\phi_n]}$, and hence  $C=M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B$. It is easy to observe that
$C=M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B$. It is easy to observe that  $M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ is a unitary operator and
$M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ is a unitary operator and
 \begin{equation*}
M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B =I,
\end{equation*}
\begin{equation*}
M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B =I,
\end{equation*}and hence
 \begin{equation*}
\mathscr{C}_B M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B = M^*_{[\phi_1,\phi_2,\ldots ,\phi_n]},
\end{equation*}
\begin{equation*}
\mathscr{C}_B M_{[\phi_1,\phi_2,\ldots ,\phi_n]}\mathscr{C}_B = M^*_{[\phi_1,\phi_2,\ldots ,\phi_n]},
\end{equation*}implying that
 $M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ is
$M_{[\phi_1,\phi_2,\ldots ,\phi_n]}$ is  $\mathscr{C}_B$-symmetric.
$\mathscr{C}_B$-symmetric.(ii) Let C be a conjugation on L 2 such that
 $CM_B=M_BC$. Then again, using (6.2), we conclude that the unitary operator
$CM_B=M_BC$. Then again, using (6.2), we conclude that the unitary operator  $C\circ \mathscr{C}_B^\star$ also commutes with MB, and hence by Theorem 2.2, there exist
$C\circ \mathscr{C}_B^\star$ also commutes with MB, and hence by Theorem 2.2, there exist  $\psi_1,\psi_2, \ldots , \psi_n \in L^\infty$ such that
$\psi_1,\psi_2, \ldots , \psi_n \in L^\infty$ such that
 \begin{equation*}C \circ \mathscr{C}^\star_B = M_{[\psi_1,\psi_2,\ldots ,\psi_n]}\end{equation*}
\begin{equation*}C \circ \mathscr{C}^\star_B = M_{[\psi_1,\psi_2,\ldots ,\psi_n]}\end{equation*}which implies
 $C = M_{[\psi_1,\psi_2,\ldots ,\psi_n]}\mathscr{C}^\star_B $. Similarly, as in (i),
$C = M_{[\psi_1,\psi_2,\ldots ,\psi_n]}\mathscr{C}^\star_B $. Similarly, as in (i),  $M_{[\psi_1,\psi_2,\ldots ,\psi_n]}$ is unitary and
$M_{[\psi_1,\psi_2,\ldots ,\psi_n]}$ is unitary and  $\mathscr{C}_B^\star$-symmetric.
$\mathscr{C}_B^\star$-symmetric.
Now, we turn our discussion to find the relations between MB-commuting conjugations and model spaces for ![]() $B(z)=z^n$. Observe that the actions of
$B(z)=z^n$. Observe that the actions of ![]() $\mathscr{C}_{B}$ and
$\mathscr{C}_{B}$ and ![]() $\mathscr{C}_B^\star$ are same on KB. The action of
$\mathscr{C}_B^\star$ are same on KB. The action of ![]() $\mathscr{C}_{z^n}$ on the set
$\mathscr{C}_{z^n}$ on the set ![]() $\{1,z,\ldots,z^{n-1}\}$ is given by
$\{1,z,\ldots,z^{n-1}\}$ is given by ![]() $\mathscr{C}_{z^n}(z^k)= z^{(n-1)-k}$ for
$\mathscr{C}_{z^n}(z^k)= z^{(n-1)-k}$ for ![]() $0\leq k \leq n-1$. Depending on n, we have the following two cases:
$0\leq k \leq n-1$. Depending on n, we have the following two cases:
(1) If n is odd, then the action of
 $\mathscr{C}_{z^n}$ is the following
(6.3)
$\mathscr{C}_{z^n}$ is the following
(6.3) \begin{align}
\begin{array}{|c| c| c| c| c| c| c| c| c|c|c|}
\hline
&&&&&&&&&&\\[-9pt]
1 & z & z^2 & \cdots & z^{\frac{n-3}{2}} & z^{\frac{n-1}{2}} & z^{\frac{n+1}{2}} & \cdots & z^{n-3} & z^{n-2} & z^{n-1} \\
\hline
&&&&&&&&&&\\[-9pt]
z^{n-1} & z^{n-2} & z^{n-3} & \cdots & z^{\frac{n+1}{2}} & z^{\frac{n-1}{2}} & z^{\frac{n-3}{2}} & \cdots & z^2 & z & 1 \\
\hline
\end{array},
\end{align}
\begin{align}
\begin{array}{|c| c| c| c| c| c| c| c| c|c|c|}
\hline
&&&&&&&&&&\\[-9pt]
1 & z & z^2 & \cdots & z^{\frac{n-3}{2}} & z^{\frac{n-1}{2}} & z^{\frac{n+1}{2}} & \cdots & z^{n-3} & z^{n-2} & z^{n-1} \\
\hline
&&&&&&&&&&\\[-9pt]
z^{n-1} & z^{n-2} & z^{n-3} & \cdots & z^{\frac{n+1}{2}} & z^{\frac{n-1}{2}} & z^{\frac{n-3}{2}} & \cdots & z^2 & z & 1 \\
\hline
\end{array},
\end{align}where the first row contains the basis elements and the second row contains their images, respectively.
(2) If n is even, then as above the action of
 $\mathscr{C}_{z^n}$ is as follows:
(6.4)
$\mathscr{C}_{z^n}$ is as follows:
(6.4) \begin{align}
\begin{array}{|c| c| c| c| c| c| c| c|c|c|}
\hline
&&&&&&&&&\\[-9pt]
1 & z & z^2 & \cdots & z^{\frac{n}{2}-1} & z^{\frac{n}{2}} & \cdots & z^{n-3} & z^{n-2} & z^{n-1} \\
\hline
&&&&&&&&&\\[-9pt]
z^{n-1} & z^{n-2} & z^{n-3} & \cdots & z^{\frac{n}{2}} & z^{\frac{n}{2}-1} & \cdots & z^2 & z & 1 \\
\hline
\end{array}.
\end{align}
\begin{align}
\begin{array}{|c| c| c| c| c| c| c| c|c|c|}
\hline
&&&&&&&&&\\[-9pt]
1 & z & z^2 & \cdots & z^{\frac{n}{2}-1} & z^{\frac{n}{2}} & \cdots & z^{n-3} & z^{n-2} & z^{n-1} \\
\hline
&&&&&&&&&\\[-9pt]
z^{n-1} & z^{n-2} & z^{n-3} & \cdots & z^{\frac{n}{2}} & z^{\frac{n}{2}-1} & \cdots & z^2 & z & 1 \\
\hline
\end{array}.
\end{align}
Also, note that ![]() $\mathscr{C}_{z^n}=M_{z^{n-1}}J$, and
$\mathscr{C}_{z^n}=M_{z^{n-1}}J$, and
 \begin{equation}
\mathscr{C}^\star_{z^n}=
\begin{cases}
M_{[z^{n-1},z^{n-3},\ldots ,z^2,1,\bar{z}^2, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star , ~\text{if~n~is ~odd,}\\
M_{[z^{n-1},z^{n-3},\ldots ,z,\bar{z}, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star , ~\text{if ~n ~is ~even}.
\end{cases}
\end{equation}
\begin{equation}
\mathscr{C}^\star_{z^n}=
\begin{cases}
M_{[z^{n-1},z^{n-3},\ldots ,z^2,1,\bar{z}^2, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star , ~\text{if~n~is ~odd,}\\
M_{[z^{n-1},z^{n-3},\ldots ,z,\bar{z}, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star , ~\text{if ~n ~is ~even}.
\end{cases}
\end{equation} The above two relations follow from the decomposition of ![]() $f\in L^2$ mentioned in (6.1) along with the action of
$f\in L^2$ mentioned in (6.1) along with the action of ![]() $\mathscr{C}_{z^n}$ and
$\mathscr{C}_{z^n}$ and ![]() $\mathscr{C}^\star_{z^n}$, respectively. Now we are in a position to state and prove our second main result in this section, which generalizes Theorem 5.1. Nevertheless, we have more explicit expressions of ξ 1 and ξ 2 in Theorem 5.1 for
$\mathscr{C}^\star_{z^n}$, respectively. Now we are in a position to state and prove our second main result in this section, which generalizes Theorem 5.1. Nevertheless, we have more explicit expressions of ξ 1 and ξ 2 in Theorem 5.1 for ![]() $B(z)=z^2$, in compare to the following theorem for the case
$B(z)=z^2$, in compare to the following theorem for the case ![]() $B(z)=z^n$,
$B(z)=z^n$, ![]() $n\geq 3$.
$n\geq 3$.
Theorem 6.2. Let C be a conjugation on L 2 such that ![]() $CM_{z^n} =M_{z^n} C$ and let C preserve the Hardy space H 2, then
$CM_{z^n} =M_{z^n} C$ and let C preserve the Hardy space H 2, then ![]() $C = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star$, where
$C = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star$, where ![]() $\xi_1 ,z\xi_2,z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty $ and
$\xi_1 ,z\xi_2,z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty $ and ![]() $M_{[\xi_1,\xi_2, \ldots ,\xi_n]}$ is a
$M_{[\xi_1,\xi_2, \ldots ,\xi_n]}$ is a ![]() $J^\star$-symmetric unitary operator.
$J^\star$-symmetric unitary operator.
Proof. By using Theorem 6.1, there exist ![]() $\psi_1, \psi_2 , \ldots , \psi_n \in
L^\infty$ such that
$\psi_1, \psi_2 , \ldots , \psi_n \in
L^\infty$ such that ![]() $C=M_{[\psi_1,\psi_2, \ldots ,\psi_n]}C^\star_{z^n}$. Now from (6.5), we get,
$C=M_{[\psi_1,\psi_2, \ldots ,\psi_n]}C^\star_{z^n}$. Now from (6.5), we get,
 \begin{equation*}
C=
\begin{cases}
M_{[\psi_1,\psi_2, \ldots ,\psi_n]}M_{[z^{n-1},z^{n-3},\ldots ,z^2,1,\bar{z}^2, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star ,~\text{if~n~is ~odd},\\
M_{[\psi_1,\psi_2, \ldots ,\psi_n]}M_{[z^{n-1},z^{n-3},\ldots ,z,\bar{z},\bar{z}^3, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star , ~\text{if ~n ~is ~even}.
\end{cases}
\end{equation*}
\begin{equation*}
C=
\begin{cases}
M_{[\psi_1,\psi_2, \ldots ,\psi_n]}M_{[z^{n-1},z^{n-3},\ldots ,z^2,1,\bar{z}^2, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star ,~\text{if~n~is ~odd},\\
M_{[\psi_1,\psi_2, \ldots ,\psi_n]}M_{[z^{n-1},z^{n-3},\ldots ,z,\bar{z},\bar{z}^3, \ldots ,\bar{z}^{n-3},\bar{z}^{n-1}]} J^\star , ~\text{if ~n ~is ~even}.
\end{cases}
\end{equation*}Next, we divide our analysis into the following two cases.
(i) Let n be an odd natural number.
Now, we rewrite C as follows:
 \begin{align*}
C & = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star,
\end{align*}
\begin{align*}
C & = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star,
\end{align*}where
 $\xi_1 = z^{n-1}\psi_n, \xi_2 = z^{n-3}\psi_{n-1} ,\ldots ,\xi_{\frac{n-1}{2}}= z^2 \psi_{\frac{n+3}{2}} ,\xi_{\frac{n+1}{2}} = \psi_{\frac{n+1}{2}} ,\xi_{\frac{n+3}{2}} = \bar{z}^2\psi_{\frac{n-1}{2}}, \ldots$,
$\xi_1 = z^{n-1}\psi_n, \xi_2 = z^{n-3}\psi_{n-1} ,\ldots ,\xi_{\frac{n-1}{2}}= z^2 \psi_{\frac{n+3}{2}} ,\xi_{\frac{n+1}{2}} = \psi_{\frac{n+1}{2}} ,\xi_{\frac{n+3}{2}} = \bar{z}^2\psi_{\frac{n-1}{2}}, \ldots$,  $ \xi_n = \bar{z}^{n-1}\psi_1 $. Therefore, by proceeding similarly as in Theorem 6.1, we conclude that
$ \xi_n = \bar{z}^{n-1}\psi_1 $. Therefore, by proceeding similarly as in Theorem 6.1, we conclude that  $M_{[\xi_1,\xi_2, \ldots ,\xi_n]}$ is a unitary operator and
$M_{[\xi_1,\xi_2, \ldots ,\xi_n]}$ is a unitary operator and  $J^\star$-symmetric. Since
$J^\star$-symmetric. Since  $C(H^2)\subset H^2$, then we conclude
$C(H^2)\subset H^2$, then we conclude  $\xi_1 ,z\xi_2,$
$\xi_1 ,z\xi_2,$  $z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty$.
$z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty$.(ii) Let n be an even natural number.
Like case (i), we again rewrite C as follows
 \begin{align*}
C & = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star,
\end{align*}
\begin{align*}
C & = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star,
\end{align*}where
 $\xi_1 = z^{n-1}\psi_n, \xi_2 = z^{n-3}\psi_{n-1} ,\ldots ,\xi_{\frac{n}{2}}= z \psi_{\frac{n}{2}+1} ,\xi_{\frac{n}{2}+1} = \bar{z}\psi_{\frac{n}{2}} ,\ldots$,
$\xi_1 = z^{n-1}\psi_n, \xi_2 = z^{n-3}\psi_{n-1} ,\ldots ,\xi_{\frac{n}{2}}= z \psi_{\frac{n}{2}+1} ,\xi_{\frac{n}{2}+1} = \bar{z}\psi_{\frac{n}{2}} ,\ldots$,  $ \xi_n = \bar{z}^{n-1}\psi_1 $. Similarly, using the invariance property
$ \xi_n = \bar{z}^{n-1}\psi_1 $. Similarly, using the invariance property  $C(H^2)\subset H^2$, we conclude
$C(H^2)\subset H^2$, we conclude  $\xi_1 ,z\xi_2,z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty $.
$\xi_1 ,z\xi_2,z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty $.
Therefore in both cases ![]() $C = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star$, where
$C = M_{[\xi_1,\xi_2, \ldots ,\xi_n]}J^\star$, where ![]() $\xi_1 ,z\xi_2,z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty $. Moreover, it is easy to check that
$\xi_1 ,z\xi_2,z^2\xi_3, \ldots ,z^{n-1}\xi_n \in H^\infty $. Moreover, it is easy to check that ![]() $M_{[\xi_1,\xi_2, \ldots ,\xi_n]}$ is a unitary operator and
$M_{[\xi_1,\xi_2, \ldots ,\xi_n]}$ is a unitary operator and ![]() $J^\star$-symmetric.
$J^\star$-symmetric.
Finally, we have the following interesting result.
Theorem 6.3. There is no conjugation C on L 2 for which ![]() $M_{z^n}$ is
$M_{z^n}$ is ![]() $C-$symmetric and
$C-$symmetric and ![]() $C(H^2)\subset H^2$.
$C(H^2)\subset H^2$.
Proof. Let C be a conjugation on L 2 such that ![]() $CM_{z^n}C =M_{\bar{z}^n} $ and
$CM_{z^n}C =M_{\bar{z}^n} $ and ![]() $C(H^2)\subset H^2$. Therefore by applying Theorem 6.1 we get,
$C(H^2)\subset H^2$. Therefore by applying Theorem 6.1 we get,
where ![]() $\zeta_1=z^{n-1} \phi_n ,\zeta_2 = z^{n-1} \phi_1 ,\zeta_3 = z^{n-1} \phi_2, \ldots ,\zeta_n =z^{n-1}\phi_{n-1} .$ Moreover, the fact
$\zeta_1=z^{n-1} \phi_n ,\zeta_2 = z^{n-1} \phi_1 ,\zeta_3 = z^{n-1} \phi_2, \ldots ,\zeta_n =z^{n-1}\phi_{n-1} .$ Moreover, the fact ![]() $C(H^2)\subset H^2$ implies
$C(H^2)\subset H^2$ implies ![]() $\zeta_1,\zeta_2, \ldots , \zeta_n \in H^\infty$. Now by using (6.6), we get for any
$\zeta_1,\zeta_2, \ldots , \zeta_n \in H^\infty$. Now by using (6.6), we get for any ![]() $k\geq 0$.
$k\geq 0$.
and hence ![]() $\zeta_1
=0$. By mimicking a similar kind of argument, we conclude
$\zeta_1
=0$. By mimicking a similar kind of argument, we conclude ![]() $\zeta_{i} = 0$ for
$\zeta_{i} = 0$ for ![]() $2\leq i \leq n$. On the other hand,
$2\leq i \leq n$. On the other hand, ![]() $ M_{[\zeta_1,\zeta_2,\ldots ,\zeta_n]}=CJ$ is an unitary operator, a contradiction. This completes the proof.
$ M_{[\zeta_1,\zeta_2,\ldots ,\zeta_n]}=CJ$ is an unitary operator, a contradiction. This completes the proof.
We end the article with the following question:
Question 3. What is the complete characterization for the class of conjugations that either commute with MB or intertwine the operators MB and ![]() $M_{\overline{B}}$ together with the invariant property of various subspaces of L 2 corresponding to any arbitrary finite Blaschke product B?
$M_{\overline{B}}$ together with the invariant property of various subspaces of L 2 corresponding to any arbitrary finite Blaschke product B?
Acknowledgements
The authors would like to thank Chandan Pradhan for the helpful discussions. We would also like to thank Srijan Sarkar for introducing this area to us. The research of the first-named author is supported by the Mathematical Research Impact Centric Support (MATRICS) grant, File No. MTR/2019/000640 , by the Science and Engineering Research Board (SERB), Department of Science & Technology (DST), Government of India. The second named author gratefully acknowledges the support provided by IIT Guwahati, Government of India. We sincerely thank the referee for several suggestions which considerably improved the presentation of this paper.