Article contents
A Derivation of Certain Variational Principles for Mixed Boundary Value Problems in Potential Theory
Published online by Cambridge University Press: 20 January 2009
Extract
We consider the following problem: A potential function φ satisfies Laplace's equation ∇2φ = φxx + φyy = 0 in a region R bounded by a closed curve C on which mixed boundary conditions are specified, i.e. φ = f(s) on a part A of the boundary and ∂φ/∂n = g(s) on a part B, where C = A + B and distance along C is denoted by s. Electrostatic problems of this type have been solved approximately in (1) and (2) by formulating them in terms of integral equations and then applying variational principles to the integral equations. In that approach, attention is concentrated on integrals over the boundary of the region R. The most common type of variational principle for potential problems involves integrals over the region R rather than integrals over the boundary of R. An example is given by the Rayleigh-Ritz method which depends on the stationary character of Dirichlet's integral
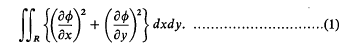
In this paper we show that the variational principles used in (1), (2), are closely connected with the more usual type of variational principles, by deriving the principles used in (1), (2) from inequalities deduced by considering integrals of type (1) over the region R.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1961
References
REFERENCES
- 2
- Cited by




