Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-24T10:14:30.862Z Has data issue: false hasContentIssue false
  • English
  • Français

The dynamics of linearized polynomials

Published online by Cambridge University Press:  20 January 2009

Stephen D. Cohen  and
Dirk Hachenberger
Stephen D. Cohen
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, UK (sdc@maths.gla.ac.uk)
Dirk Hachenberger
Affiliation:
Institut für Mathematik, Universität Augsburg, 86159 Augsburg, Germany (dirk.hachenberger@math.uni-augsburg.de)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F = GF(q). To any polynomial G ∈ F[x] there is associated a mapping Ĝ on the set IF of monic irreducible polynomials over F. We present a natural and effective theory of the dynamics of Ĝ for the case in which G is a monic q-linearized polynomial. The main outcome is the following theorem.

Assume that G is not of the form 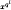, where l ≥ 0 (in which event the dynamics is trivial). Then, for every integer n ≥ 1 and for every integer k ≥ 0, there exist infinitely many μ ∈ IF. having preperiod k and primitive period n with respect to Ĝ.

Previously, Morton, by somewhat different means, had studied the primitive periods of Ĝ when G = xq – ax, α a non-zero element of F. Our theorem extends and generalizes Morton's result. Moreover, it establishes a conjecture of Morton for the class of q-linearized polynomials.

Keywords

finite fieldpolynomial dynamicslinearized polynomialperiod
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 43 , Issue 1 , February 2000 , pp. 113 - 128
Copyright
Copyright © Edinburgh Mathematical Society 2000

References

1.Batra, A. and Morton, P., Algebraic dynamics of polynomial maps on the algebraic closure of a finite field, I, Rocky Mountain J. Math. 24 (1994), 453–481.Google Scholar
2.Batra, A. and Morton, P., Algebraic dynamics of polynomial maps on the algebraic closure of a finite field, II, Rocky Mountain J. Math. 24 (1994), 905–932.Google Scholar
3.Carlitz, L., Sets of primitive roots, Compos. Math. 13 (1956), 65–70.Google Scholar
4.Cohen, S. D., Primitive roots and powers among values of polynomials over finite fields, J. Reine Angew. Math. 350 (1984), 137–151.Google Scholar
5.Cohen, S. D., Primitive elements and polynomials: existence results, in Proc. 1st Int. Conf. on Finite Fields and Applications (ed. Mullen, G. L. and Shiue, P. J.-S.), Lecture Notes in Pure and Applied Mathematics, vol. 141, pp. 43–55 (Dekker, 1993).Google Scholar
6.Hachenberger, D., Finite fields: normal bases and completely free elements (Kluwer, Boston, 1997).CrossRefGoogle Scholar
7.Hachenberger, D., Finite fields: algebraic closure and module structures (Forschungsbericht, Deutsche Forschungsgemeinschaft, 1997).CrossRefGoogle Scholar
8.Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, 5th edn (Oxford University Press, 1979).Google Scholar
9.Morton, P., Periods of maps on irreducible polynomials over finite fields, Finite Fields Applic. 3 (1997), 11–24.CrossRefGoogle Scholar
10.Ore, O., Contributions to the theory of finite fields, Trans. Am. Math. Soc. 36 (1934), 243–274.CrossRefGoogle Scholar
11.Lidl, R. and Niederreiter, H., Finite fields (Addison-Wesley, Reading, MA, 1983).Google Scholar
12.Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers, Illinois J. Math. 6 (1962), 64–94.CrossRefGoogle Scholar
13.Vivaldi, F., Dynamics over irreducible polynomials, Nonlinearity 5 (1992), 941–960.CrossRefGoogle Scholar