Hostname: page-component-7479d7b7d-q6k6v Total loading time: 0 Render date: 2024-07-09T22:23:38.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact formulae and Turán inequalities for Vafa–Witten invariants of 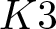$K3$ surfaces

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  08 August 2023

Daniel R. Johnston  and
Joshua Males Open the ORCID record for Joshua Males [Opens in a new window]
Daniel R. Johnston
Affiliation:
School of Science, The University of New South Wales, Canberra, ACT, Australia (daniel.johnston@adfa.edu.au)
Joshua Males
Affiliation:
Department of Mathematics, Machray Hall, University of Manitoba, Winnipeg, Canada (joshua.males@umanitoba.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider three different families of Vafa–Witten invariants of 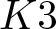$K3$ surfaces. In each case, the partition function that encodes the Vafa–Witten invariants is given by combinations of twisted Dedekind η-functions. By utilizing known properties of these η-functions, we obtain exact formulae for each of the invariants and prove that they asymptotically satisfy all higher-order Turán inequalities.

Keywords

Vafa–Witten invariantsexact formulaeasymptoticsTurán inequalities

MSC classification

Primary: 11F12: Automorphic forms, one variable 11F23: Relations with algebraic geometry and topology
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 3 , August 2023 , pp. 845 - 861
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, G. E., Askey, R. and Roy, R., Special functions, Volume 1 (Cambridge University Press, 1999).CrossRefGoogle Scholar
Apostol, T. M., Modular functions and Dirichlet series in number theory (Springer-Verlag, New York, 1990).CrossRefGoogle Scholar
Bringmann, K., Craig, W., Males, J. and Ono, K., Distributions on partitions arising from Hilbert schemes and hook lengths Forum Math. Sigma, 10 (2022), .CrossRefGoogle Scholar
Bringmann, K., Jennings-Shaffer, C., Mahlburg, K. and Rhoades, R., Peak positions of strongly unimodal sequences, Trans. Amer. Math. Soc. 372(10) (2019), 7087–7109.CrossRefGoogle Scholar
Bruinier, J. and Ono, K., Algebraic formulas for the coefficients of half-integral weight harmonic weak Maass forms, Adv. Math. 246 (2013), 198–219.CrossRefGoogle Scholar
Cesana, G., Craig, W. and Males, J., Asymptotic equidistribution for partition statistics and topological invariants, preprint.Google Scholar
Craig, W. and Pun, A., A note on the higher order Turán inequalities for k-regular partitions, Res. Number Theory 7(1) (2021), .CrossRefGoogle Scholar
DeSalvo, S. and Pak, I., Log-concavity of the partition function, Ramanujan J. 38(1) (2015), 61–73.CrossRefGoogle Scholar
Dimitrov, D., Higher order Turán inequalities, Proc. Amer. Math. Soc. 126(7) (1998), 2033–2037.CrossRefGoogle Scholar
Griffin, M., Ono, K., Rolen, K. L. and Zagier, D., Jensen polynomials for the Riemann zeta function and other sequences, Proc. Natl. Acad. Sci. USA 116(23) (2019), 11103–11110.CrossRefGoogle ScholarPubMed
Griffin, M., Ono, K., Rolen, L., Thorner, J., Tripp, Z. and Wagner, I., Jensen polynomials for the Riemann xi-function, Adv. Math. 397 (2022), .CrossRefGoogle Scholar
Iskander, J., Jain, V. and Talvola, V., Exact formulae for the fractional partition functions, Res. Number Theory 6(2) (2020), .CrossRefGoogle Scholar
Iwaniec, H., Topics in classical automorphic forms. Graduate Studies in Mathematics, Volume 17, (American Mathematical Society, Providence, RI, 1997).CrossRefGoogle Scholar
Jiang, Y., Counting twisted sheaves and S-duality, Adv. Math. 400 (2022), .CrossRefGoogle Scholar
Jiang, Y. and Kool, M., Twisted sheaves and $SU(r)/\mathbb{Z}_r$ Vafa–Witten theory, Math. Ann. 382(1–2) (2021), 719–743.CrossRefGoogle Scholar
Larson, H. and Wagner, I., Hyperbolicity of the partition Jensen polynomials, Res. Number Theory 5(2) (2019), .Google Scholar
Males, J., Asymptotic equidistribution and convexity for partition ranks, Ramanujan J. 54(2) (2021), 397–413.CrossRefGoogle Scholar
Pribitkin, W. and Williams, B., Short proof of Rademacher’s formula for partitions, Res. Number Theory 5(2) (2019), .CrossRefGoogle Scholar
Rademacher, H., A convergent series for the partition function p(n), Proc. Natl. Acad. Sci. USA 23(2) (1937), 78–84.CrossRefGoogle ScholarPubMed
Schur, J. and Pólya, G., Über zwei Arten von Faktorenfolgen in der Theorie der algebraischen Gleichungen, J. Reine Angew. Math. 144 (1914), 89–113.CrossRefGoogle Scholar
Szegö, G., On an inequality of P. Turán concerning Legendre polynomials, Bull. Amer. Math. Soc. 54 (1948), 401–405.CrossRefGoogle Scholar
Tanaka, Y. and Thomas, R., Vafa-Witten invariants for projective surfaces II: semistable case, Pure Appl. Math. Q. 13(3) (2017), 517–562.CrossRefGoogle Scholar
Thomas, R., Equivariant K-theory and refined Vafa-Witten invariants, Comm. Math. Phys. 378 (2020), .CrossRefGoogle Scholar
Vafa, C. and Witten, E., A strong coupling test of S-duality, Nuclear Phys. B 431(1–2) (1994), 3–77.CrossRefGoogle Scholar
Wagner, I., On a new class of Laguerre-Pólya type functions with applications in number theory, Pacific J. Math. 320(1) (2022), 177–192.CrossRefGoogle Scholar
Zuckerman, H., On the coefficients of certain modular forms belonging to subgroups of the modular group, Trans. Amer. Math. Soc. 45 (1939), 298–321.CrossRefGoogle Scholar