When a given frequency distribution is to be graduated, it is customary to express the constants of the fitted curve in terms of the moments of the frequency distribution. The rth moment of the distribution, in which the relative frequency of a measure x is φ(x) or, in the case of a continuous variable, the differential of frequency is φ(x)dx, is defined in the respective cases by

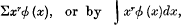
the summation or integration being taken over the whole range of possible values of x. In the present paper we make use of another kind of moment, the factorial moment, which has already been considered by several writers, and which is specially suited to the case when the frequencies of the distribution are given for discrete, equidistant values of the variable. The (r + 1)th factorial moment, for the case where x, measured from some arbitrary origin, can increase by increments h, 2h, 3h,.…, will be defined to be

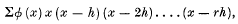
where the summation extends over all possible values of x; it will be denoted by m(r+1). By a suitable choice of scale the increments of x may be taken as equal to unity in any given case.