Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-08T03:08:57.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Factoriality and Type Classification of k-Graph von Neumann Algebras

Part of: Linear spaces and algebras of operators Selfadjoint operator algebras

Published online by Cambridge University Press:  02 November 2016

Dilian Yang
Dilian Yang*
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, ON N9B 3P4, Canada (dyang@uwindsor.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 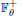be a single vertex k-graph and let 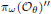be the von Neumann algebra induced from the Gelfand–Naimark–Segal (GNS) representation of a distinguished state ω of its k-graph C*-algebra 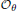. In this paper we prove the factoriality of 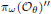, and furthermore determine its type when either 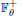has the little pullback property, or the intrinsic group of 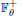has rank 0. The key step to achieving this is to show that the fixed-point algebra of the modular action corresponding to ω has a unique tracial state.

Keywords

k-graphk-graph C*-algebrak-graph von Neumann algebrafactorialitytype classificationintrinsic group

MSC classification

Secondary: 46L36: Classification of factors 47L65: Crossed product algebras (analytic crossed products) 46L10: General theory of von Neumann algebras 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 2 , May 2017 , pp. 499 - 518
Copyright
Copyright © Edinburgh Mathematical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)