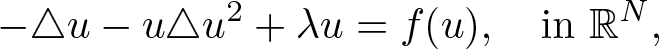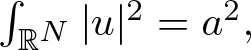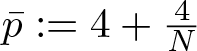1. Introduction and main results
In this paper,Footnote 1 we study the following quasilinear Schrödinger equation:
which is often referred as modified nonlinear Schrödinger equation. This kind of equations arise when ones are looking for standing waves ![]() $\psi(t,x)=e^{-i\lambda t}u(x)$ for the time-dependent quasilinear Schrödinger equation:
$\psi(t,x)=e^{-i\lambda t}u(x)$ for the time-dependent quasilinear Schrödinger equation:
 \begin{equation}
\left\{\begin{aligned}&i\partial_{t}\psi+\Delta\psi+\kappa\rho{'}(|\psi|^{2})\psi\Delta(\rho(|\psi|^{2}))+f(|\psi|^{2})\psi=0,\quad{\rm in}\ \mathbb{R}^{+}\times \mathbb{R}^{N},\\
&\psi(0,x)=\psi_{0}(x),\quad{\rm in}\ \mathbb{R}^{N},
\end{aligned}
\right.
\end{equation}
\begin{equation}
\left\{\begin{aligned}&i\partial_{t}\psi+\Delta\psi+\kappa\rho{'}(|\psi|^{2})\psi\Delta(\rho(|\psi|^{2}))+f(|\psi|^{2})\psi=0,\quad{\rm in}\ \mathbb{R}^{+}\times \mathbb{R}^{N},\\
&\psi(0,x)=\psi_{0}(x),\quad{\rm in}\ \mathbb{R}^{N},
\end{aligned}
\right.
\end{equation} where ![]() $\kappa\in\mathbb{R}$ is a constant, ρ and f are real functions. We would like to mention that quasilinear equation in form of (1.2) appears in many respects of mathematical physics. Moreover, (1.2) has been derived as models of several phenomena corresponding to the existence of various types of nonlinear term ρ. In particular, the case
$\kappa\in\mathbb{R}$ is a constant, ρ and f are real functions. We would like to mention that quasilinear equation in form of (1.2) appears in many respects of mathematical physics. Moreover, (1.2) has been derived as models of several phenomena corresponding to the existence of various types of nonlinear term ρ. In particular, the case ![]() $\rho(s)=s$ is used for the superfluid film equation in plasma physics by Kurihura [Reference Kurihura21].
$\rho(s)=s$ is used for the superfluid film equation in plasma physics by Kurihura [Reference Kurihura21].
The semilinear case κ = 0 has been widely studied in the past decades with general nonlinearity. Wei and Wu [Reference Wei and Wu42] studied normalized solutions for Schrodinger equations with critical Sobolev exponent and mixed nonlinearities, they proved the existence and non-existence of ground states and precisely asymptotic behaviours of ground states and mountain-pass type solutions as parameters go to their boundary, their studies answered some open questions proposed by Soave [Reference Soave37]. We also refer the reader to [Reference Ambrosetti, Badiale and Cingolani3, Reference Ao and Zou5, Reference Barstch and Wang7, Reference Barstch, Wang, Willem and Quittner8, Reference Rabinowitz32, Reference Tang39, Reference Tang40, Reference Zhang and Zhao46] and references therein for more valuable results. Compared to the semilinear case, the quasilinear case (κ = 1) becomes much more challenging due to the existence of the non-convex term ![]() $u\Delta u^{2}$. One of the main difficulties of (1.1) is that the energy functional is non-differentiable in
$u\Delta u^{2}$. One of the main difficulties of (1.1) is that the energy functional is non-differentiable in ![]() $W^{1,2}(\mathbb{R}^{N})$ when
$W^{1,2}(\mathbb{R}^{N})$ when ![]() $N\geq2$, see [Reference Poppenberg, Schmitt and Wang30]. In the past two decades, there are some ideas and approaches were developed to overcome this difficulty, such as the minimization methods [Reference Poppenberg, Schmitt and Wang30] where the non-differentiability of the energy functional does not come into play, the methods of a Nehari manifold argument, see [Reference Fang and Szulkin15, Reference Liu, Wang and Wang26, Reference Ruiz and Siciliano33], the methods of changing variables [Reference Colin and Jeanjean13, Reference Liu, Wang and Wang25] which reduced the quasilinear equation to a semilinear one and used an Orlicz space framework, and a perturbation method in a series of papers [Reference Liu and Wang27–Reference Liu, Liu and Wang29] which recovered the differentiability by considering a perturbed functional on a smaller function space. Recently, Dong and Mao in [Reference Dong and Mao31] applied perturbation method and Moser’s iteration technique to study a class of general quasilinear elliptic equations which admits infinitely many negative energy solutions by establishing a new convergence theorem and a weighted space to recover the compactness.
$N\geq2$, see [Reference Poppenberg, Schmitt and Wang30]. In the past two decades, there are some ideas and approaches were developed to overcome this difficulty, such as the minimization methods [Reference Poppenberg, Schmitt and Wang30] where the non-differentiability of the energy functional does not come into play, the methods of a Nehari manifold argument, see [Reference Fang and Szulkin15, Reference Liu, Wang and Wang26, Reference Ruiz and Siciliano33], the methods of changing variables [Reference Colin and Jeanjean13, Reference Liu, Wang and Wang25] which reduced the quasilinear equation to a semilinear one and used an Orlicz space framework, and a perturbation method in a series of papers [Reference Liu and Wang27–Reference Liu, Liu and Wang29] which recovered the differentiability by considering a perturbed functional on a smaller function space. Recently, Dong and Mao in [Reference Dong and Mao31] applied perturbation method and Moser’s iteration technique to study a class of general quasilinear elliptic equations which admits infinitely many negative energy solutions by establishing a new convergence theorem and a weighted space to recover the compactness.
When looking for the solution to (1.1), a possible choice is to consider ![]() $\lambda\in\mathbb{R}$ fixed in which case it is called fixed frequency problem, and find solutions as critical points of the energy functional:
$\lambda\in\mathbb{R}$ fixed in which case it is called fixed frequency problem, and find solutions as critical points of the energy functional:
 \begin{equation}
E_{\lambda}(u)=\frac{1}{2}\int_{\mathbb{R}^{N}}(|\nabla u|^{2}+\lambda|u|^{2})+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\int_{\mathbb{R}^{N}}F(u),
\end{equation}
\begin{equation}
E_{\lambda}(u)=\frac{1}{2}\int_{\mathbb{R}^{N}}(|\nabla u|^{2}+\lambda|u|^{2})+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\int_{\mathbb{R}^{N}}F(u),
\end{equation}on the space,
 \begin{equation*}\mathcal{H}=\left\{u\in W^{1,2}(\mathbb{R}^{N}): \int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2} \lt +\infty\right\},\end{equation*}
\begin{equation*}\mathcal{H}=\left\{u\in W^{1,2}(\mathbb{R}^{N}): \int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2} \lt +\infty\right\},\end{equation*} where  $F(u)=\int_{0}^{u}f(t)dt$. It is not difficult to check that u is a weak solution to (1.1) if and only if for any
$F(u)=\int_{0}^{u}f(t)dt$. It is not difficult to check that u is a weak solution to (1.1) if and only if for any ![]() $\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$,
$\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$,
 \begin{equation*}E_{\lambda}'(u)\varphi=\lim\limits_{t\rightarrow 0^{+}}\frac{E_{\lambda}(u+t\varphi)-E_{\lambda}(u)}{t}=0.\end{equation*}
\begin{equation*}E_{\lambda}'(u)\varphi=\lim\limits_{t\rightarrow 0^{+}}\frac{E_{\lambda}(u+t\varphi)-E_{\lambda}(u)}{t}=0.\end{equation*}In this case, the existence and multiplicity of solutions to (1.1) have been intensively studied during the past decades, see [Reference Colin and Jeanjean13, Reference Fang and Szulkin15, Reference Liu, Wang and Wang25–Reference Poppenberg, Schmitt and Wang30, Reference Ruiz and Siciliano33] and their references therein. We also refer to [Reference Adachi and Watanabe1, Reference Ambrosetti and Wang4, Reference Gladiali and Squassina16, Reference Selvitella34] for the uniqueness of ground states to (1.1).
Alternatively, one can search for solutions to (1.1) having a prescribed mass:
 \begin{equation}
\int_{\mathbb{R}^{N}}|u|^2 =a^2.
\end{equation}
\begin{equation}
\int_{\mathbb{R}^{N}}|u|^2 =a^2.
\end{equation} In this case ones aim at finding a real number ![]() $\lambda\in\mathbb{R}$ and
$\lambda\in\mathbb{R}$ and ![]() $u\in W^{1,2}(\mathbb{R}^{N})$ solving (1.1) and (1.4). Indeed,
$u\in W^{1,2}(\mathbb{R}^{N})$ solving (1.1) and (1.4). Indeed, ![]() $\lambda\in\mathbb{R}$ appears as a Lagrange multiplier. This approach seems to be particularly meaningful from the physical point of view, and often offers a good insight into the dynamical properties of the stationary solutions to (1.2). In this case, solutions to (1.1) and (1.4) are critical points of the energy functional:
$\lambda\in\mathbb{R}$ appears as a Lagrange multiplier. This approach seems to be particularly meaningful from the physical point of view, and often offers a good insight into the dynamical properties of the stationary solutions to (1.2). In this case, solutions to (1.1) and (1.4) are critical points of the energy functional:
 \begin{equation}
I(u)=\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}-\int_{\mathbb{R}^{N}}F(u),
\end{equation}
\begin{equation}
I(u)=\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}-\int_{\mathbb{R}^{N}}F(u),
\end{equation}on the smooth manifold:
 \begin{equation*}\widetilde{S}(a):=\left\{u\in\mathcal{H}: \int_{\mathbb{R}^{N}}|u|^{2}=a^{2}\right\},\end{equation*}
\begin{equation*}\widetilde{S}(a):=\left\{u\in\mathcal{H}: \int_{\mathbb{R}^{N}}|u|^{2}=a^{2}\right\},\end{equation*} that is, a normalized solution to (1.1) is a  $u\in\widetilde{S}(a)$ such that there exists a
$u\in\widetilde{S}(a)$ such that there exists a ![]() $\lambda\in\mathbb{R}$ satisfying:
$\lambda\in\mathbb{R}$ satisfying:
 \begin{equation*}\int_{\mathbb{R}^{N}}\nabla u\cdot\nabla\varphi+2\int_{\mathbb{R}^{N}}(u\varphi|\nabla u|^{2}+|u|^{2}\nabla u\cdot\nabla\varphi)
+\lambda\int_{\mathbb{R}^{N}}u\varphi-\int_{\mathbb{R}^{N}}f(u)\varphi=0,\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{N}}\nabla u\cdot\nabla\varphi+2\int_{\mathbb{R}^{N}}(u\varphi|\nabla u|^{2}+|u|^{2}\nabla u\cdot\nabla\varphi)
+\lambda\int_{\mathbb{R}^{N}}u\varphi-\int_{\mathbb{R}^{N}}f(u)\varphi=0,\end{equation*} for every ![]() $\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$. Meanwhile, using this approach, a critical exponent appears, the L 2-critical exponent
$\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$. Meanwhile, using this approach, a critical exponent appears, the L 2-critical exponent  $\bar{p}=4+\frac{4}{N},$ which is derived by using a Gagliardo–Nirenberg-type inequality:
$\bar{p}=4+\frac{4}{N},$ which is derived by using a Gagliardo–Nirenberg-type inequality:
 \begin{equation}
\int_{\mathbb{R}^{N}}|u|^{p}
\leq\frac{C(p,N)}{\|Q_{p}\|_{1}^{\frac{p-2}{N+2}}}\left(\int_{\mathbb{R}^{N}}|u|^{2}\right)^{\frac{4N-p(N-2)}{2(N+2)}}
\left(4\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(p-2)}{2(N+2)}}.
\end{equation}
\begin{equation}
\int_{\mathbb{R}^{N}}|u|^{p}
\leq\frac{C(p,N)}{\|Q_{p}\|_{1}^{\frac{p-2}{N+2}}}\left(\int_{\mathbb{R}^{N}}|u|^{2}\right)^{\frac{4N-p(N-2)}{2(N+2)}}
\left(4\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(p-2)}{2(N+2)}}.
\end{equation}The above inequality is related to a sharp Gagliardo–Nirenberg inequality [Reference Agueh2]:
 \begin{equation}
\int_{\mathbb{R}^{N}}|u|^{\frac{p}{2}}
\leq\frac{C(p,N)}{\|Q_{p}\|_{1}^{\frac{p-2}{N+2}}}\left(\int_{\mathbb{R}^{N}}|u|\right)^{\frac{4N-p(N-2)}{2(N+2)}}
\left(\int_{\mathbb{R}^{N}}|\nabla u|^{2}\right)^{\frac{N(p-2)}{2(N+2)}}, \quad \forall u\in \mathcal{E}^{1},
\end{equation}
\begin{equation}
\int_{\mathbb{R}^{N}}|u|^{\frac{p}{2}}
\leq\frac{C(p,N)}{\|Q_{p}\|_{1}^{\frac{p-2}{N+2}}}\left(\int_{\mathbb{R}^{N}}|u|\right)^{\frac{4N-p(N-2)}{2(N+2)}}
\left(\int_{\mathbb{R}^{N}}|\nabla u|^{2}\right)^{\frac{N(p-2)}{2(N+2)}}, \quad \forall u\in \mathcal{E}^{1},
\end{equation} where ![]() $2 \lt p \lt 2\cdot2^{*}$,
$2 \lt p \lt 2\cdot2^{*}$,
 \begin{equation*}C(p,N)=\frac{p(N+2)}{[4N-(N-2)p]^{\frac{4-N(p-2)}{2(N+2)}}[2N(p-2)]^{\frac{N(p-2)}{2(N+2)}}},\end{equation*}
\begin{equation*}C(p,N)=\frac{p(N+2)}{[4N-(N-2)p]^{\frac{4-N(p-2)}{2(N+2)}}[2N(p-2)]^{\frac{N(p-2)}{2(N+2)}}},\end{equation*} with the norm ![]() $\|u\|_{\mathcal{E}^{q}}:=|\nabla u|_{2}+|u|_{q}$ and Qp is the unique positive solution to the following equation [Reference Serrin and Tang35].
$\|u\|_{\mathcal{E}^{q}}:=|\nabla u|_{2}+|u|_{q}$ and Qp is the unique positive solution to the following equation [Reference Serrin and Tang35].
 \begin{equation*}-\Delta u+1=u^{\frac{p}{2}-1},\quad {\rm in}\ \mathbb{R}^{N}.\end{equation*}
\begin{equation*}-\Delta u+1=u^{\frac{p}{2}-1},\quad {\rm in}\ \mathbb{R}^{N}.\end{equation*} L 2-critical exponent ![]() $\bar{p}$ is the threshold exponent for many dynamical properties. From the variational point of view,
$\bar{p}$ is the threshold exponent for many dynamical properties. From the variational point of view, ![]() $\bar{p}$ decides that I(u) is bounded or unbounded from below on
$\bar{p}$ decides that I(u) is bounded or unbounded from below on  $\widetilde{S}(a)$.
$\widetilde{S}(a)$.
If ![]() $f(u)=|u|^{p-2}u$, for the L 2-subcritical case
$f(u)=|u|^{p-2}u$, for the L 2-subcritical case ![]() $2 \lt p \lt \bar{p}$, to avoid the non-differentiability of
$2 \lt p \lt \bar{p}$, to avoid the non-differentiability of  $\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}$, Colin et al. [Reference Colin, Jeanjean and Squassina14] studied the minimization problem
$\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}$, Colin et al. [Reference Colin, Jeanjean and Squassina14] studied the minimization problem
 \begin{equation}
\widetilde{m}(a)=\inf\limits_{u\in\widetilde{S}(a)}I(u) \gt -\infty,
\end{equation}
\begin{equation}
\widetilde{m}(a)=\inf\limits_{u\in\widetilde{S}(a)}I(u) \gt -\infty,
\end{equation}and proved the existence and some properties such as orbital stability or instability of the normalized solutions to (1.1). Inspired by [Reference Colin, Jeanjean and Squassina14], Jeanjean et al. [Reference Jeanjean and Luo20] also considered the minimization problem (1.8) and extended some results of Colin et al. [Reference Colin, Jeanjean and Squassina14]. After that, Zeng et al. [Reference Zeng and Zhang45] studied the existence and asymptotic behaviour of the minimizers to:
 \begin{equation*}\inf\limits_{u\in\widetilde{S}(a)}\left(I(u)+\frac{1}{2}\int_{\mathbb{R}^{N}}V(x)|u|^{2}\right),\end{equation*}
\begin{equation*}\inf\limits_{u\in\widetilde{S}(a)}\left(I(u)+\frac{1}{2}\int_{\mathbb{R}^{N}}V(x)|u|^{2}\right),\end{equation*} where V(x) is an infinite potential well. For the L 2-critical case ![]() $p=\bar{p}$, we refer to [Reference Li and Zou23, Reference Ye and Yu44]. In [Reference Ye and Yu44], Ye et al. proved that the minimization problem (1.8) has no minimizer for all a > 0 and they also proved that there exists a
$p=\bar{p}$, we refer to [Reference Li and Zou23, Reference Ye and Yu44]. In [Reference Ye and Yu44], Ye et al. proved that the minimization problem (1.8) has no minimizer for all a > 0 and they also proved that there exists a ![]() $a_{*} \gt 0$ such that for
$a_{*} \gt 0$ such that for ![]() $a \gt a_{*}$ and
$a \gt a_{*}$ and ![]() $N\leq3$, (1.1) has at least one radially symmetric positive normalized solution. Based on [Reference Ye and Yu44], Li and Zou [Reference Li and Zou23] obtained a radially symmetric positive normalized solution to (1.1) with
$N\leq3$, (1.1) has at least one radially symmetric positive normalized solution. Based on [Reference Ye and Yu44], Li and Zou [Reference Li and Zou23] obtained a radially symmetric positive normalized solution to (1.1) with ![]() $N\geq4$ and
$N\geq4$ and  $a_{*} \lt a \lt \left(\frac{N-2}{N-2-\frac{4}{N}}\right)^{\frac{N}{2}}a_{*}$, in the sense that they extended some results of [Reference Ye and Yu44]. For the L 2-supercritical case
$a_{*} \lt a \lt \left(\frac{N-2}{N-2-\frac{4}{N}}\right)^{\frac{N}{2}}a_{*}$, in the sense that they extended some results of [Reference Ye and Yu44]. For the L 2-supercritical case ![]() $p \gt \bar{p}$, to our best knowledge, there are few results on this direction, only [Reference Li and Zou23]. In [Reference Li and Zou23], by using some ingenious methods, Li and Zou obtained many interesting and important results which also enlightened our work. Firstly, by the perturbation method, Li and Zou proved the existence and multiplicity of normalized solutions to (1.1) by applying the index theory. It seems that no literatures involve the case of general nonlinearities, when it is non-homogeneous and L 2-supercritical. It is also blank even for the existence. Thus, it is natural to consider the work which involves the existence and some properties of the normalized solutions to (1.1) with L 2-supercritical general nonlinearities. And one of our goals is to make some progresses in these respects.
$p \gt \bar{p}$, to our best knowledge, there are few results on this direction, only [Reference Li and Zou23]. In [Reference Li and Zou23], by using some ingenious methods, Li and Zou obtained many interesting and important results which also enlightened our work. Firstly, by the perturbation method, Li and Zou proved the existence and multiplicity of normalized solutions to (1.1) by applying the index theory. It seems that no literatures involve the case of general nonlinearities, when it is non-homogeneous and L 2-supercritical. It is also blank even for the existence. Thus, it is natural to consider the work which involves the existence and some properties of the normalized solutions to (1.1) with L 2-supercritical general nonlinearities. And one of our goals is to make some progresses in these respects.
If ![]() $f(u)=\tau|u|^{q-2}u+|u|^{p-2}u$, where τ > 0,
$f(u)=\tau|u|^{q-2}u+|u|^{p-2}u$, where τ > 0,  $2 \lt q \lt 2+\frac{4}{N}$ and
$2 \lt q \lt 2+\frac{4}{N}$ and ![]() $p \gt \bar{p}$, one can see that the (1.1) has more general nonlinearities and the interplay between L 2-subcritical and L 2-supercritical nonlinearities strongly affects the geometry of the energy functional and the existence and properties of normalized solutions. So it is more difficult to study (1.1) than the pure homogeneous nonlinearities
$p \gt \bar{p}$, one can see that the (1.1) has more general nonlinearities and the interplay between L 2-subcritical and L 2-supercritical nonlinearities strongly affects the geometry of the energy functional and the existence and properties of normalized solutions. So it is more difficult to study (1.1) than the pure homogeneous nonlinearities ![]() $|u|^{p-2}u$. For the semilinear elliptic equations with combined nonlinearities:
$|u|^{p-2}u$. For the semilinear elliptic equations with combined nonlinearities:
where ![]() $\mu\in\mathbb{R}$,
$\mu\in\mathbb{R}$,  $2 \lt q \lt 2+\frac{4}{N}$ and
$2 \lt q \lt 2+\frac{4}{N}$ and  $2+\frac{4}{N} \lt p\leq 2^{*}$. Soave [Reference Soave36, Reference Soave37] studied the existence and some properties of the ground state normalized solutions to (1.9) in a smaller function space
$2+\frac{4}{N} \lt p\leq 2^{*}$. Soave [Reference Soave36, Reference Soave37] studied the existence and some properties of the ground state normalized solutions to (1.9) in a smaller function space ![]() $\mathcal{P}^{+}$ and
$\mathcal{P}^{+}$ and ![]() $\mathcal{P}^{-}$, where the Pohozaev manifold:
$\mathcal{P}^{-}$, where the Pohozaev manifold:
This strategy was used also by other authors in order to study other type of Schrodinger equation and, according to my knowledge, a pioneering article with this tool was [Reference Tarantello41] in which G. Tarantello studied a class of non-homogeneous elliptic equations involving critical Sobolev exponent. But for the quasilinear Schrödinger equations with combined nonlinearities, to be our best knowledge, there is no work which involves this respect. Motivated by [Reference Soave36, Reference Soave37, Reference Tarantello41], it is natural to consider whether we can prove the existence and some properties of the ground state normalized solutions to (1.1) with combined nonlinearities. Hence, the other goal of this paper is devoted to giving the proof in this respect.
Our main results read as follows.
Theorem 1.1. Assume that (F1) and (F2) holds:
(F1) ![]() $f\in C(\mathbb{R},\mathbb{R})$, f ≠ 0,
$f\in C(\mathbb{R},\mathbb{R})$, f ≠ 0, ![]() $f(t)=o(t)$ as
$f(t)=o(t)$ as ![]() $t\rightarrow0$ and there exist
$t\rightarrow0$ and there exist ![]() $\alpha, \beta\in\mathbb{R}$ satisfying:
$\alpha, \beta\in\mathbb{R}$ satisfying:
such that
(F2) The function defined by  $\widetilde{F}(t):=\frac{1}{2}f(t)t-F(t)$ is of class C 1 and
$\widetilde{F}(t):=\frac{1}{2}f(t)t-F(t)$ is of class C 1 and
 \begin{equation*}\widetilde{F}'(t)t\geq\alpha\widetilde{F}(t),\ \ \ \forall \ t\in\mathbb{R},\end{equation*}
\begin{equation*}\widetilde{F}'(t)t\geq\alpha\widetilde{F}(t),\ \ \ \forall \ t\in\mathbb{R},\end{equation*} where α is given by ![]() $(F1)$.
$(F1)$.
Then for any a > 0, there exists a radially symmetric positive normalized ground state solution ![]() $u\in W^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ to (1.1) in the sense that:
$u\in W^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ to (1.1) in the sense that:
 \begin{equation*}I(u)=\inf\left\{I(v): v\in \widetilde{S}(a), I|_{\widetilde{S}(a)}'(v)=0, v\neq 0\right\}.\end{equation*}
\begin{equation*}I(u)=\inf\left\{I(v): v\in \widetilde{S}(a), I|_{\widetilde{S}(a)}'(v)=0, v\neq 0\right\}.\end{equation*}Theorem 1.2. If ![]() $f(u)=\tau|u|^{q-2}u+|u|^{p-2}u$, τ > 0 and assume that one of the following conditions holds:
$f(u)=\tau|u|^{q-2}u+|u|^{p-2}u$, τ > 0 and assume that one of the following conditions holds:
(H1) ![]() $N=1,2$,
$N=1,2$,  $2 \lt q \lt 2+\frac{4}{N}$ and
$2 \lt q \lt 2+\frac{4}{N}$ and ![]() $p \gt \bar{p}$.
$p \gt \bar{p}$.
(H2) N = 3,  $2 \lt q \lt 2+\frac{4}{N}$ and
$2 \lt q \lt 2+\frac{4}{N}$ and ![]() $\bar{p} \lt p\leq2^{*}$.
$\bar{p} \lt p\leq2^{*}$.
Let us also assume that
 \begin{equation}
\begin{aligned}&\left(\tau a^{(1-\gamma_{q})q}\right)^{p\gamma_{p}-2}\left(a^{(1-\gamma_{p})p}\right)^{2-q\gamma_{q}}\\
& \lt \left(\frac{p(2-q\gamma_{q})}{2C_{N,p}^{p}(p\gamma_{p}-q\gamma_{q})}\right)^{2-q\gamma_{q}}
\left(\frac{q(p\gamma_{p}-2)}{2C_{N,q}^{q}(p\gamma_{p}-q\gamma_{q})}\right)^{p\gamma_{p}-2},
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}&\left(\tau a^{(1-\gamma_{q})q}\right)^{p\gamma_{p}-2}\left(a^{(1-\gamma_{p})p}\right)^{2-q\gamma_{q}}\\
& \lt \left(\frac{p(2-q\gamma_{q})}{2C_{N,p}^{p}(p\gamma_{p}-q\gamma_{q})}\right)^{2-q\gamma_{q}}
\left(\frac{q(p\gamma_{p}-2)}{2C_{N,q}^{q}(p\gamma_{p}-q\gamma_{q})}\right)^{p\gamma_{p}-2},
\end{aligned}
\end{equation} where  $\gamma_{p}:=\frac{N(p-2)}{2p},\ p \gt 2$,
$\gamma_{p}:=\frac{N(p-2)}{2p},\ p \gt 2$,  $2^{*}:=\frac{2N}{N-2}$ is the Sobolev critical exponent. If
$2^{*}:=\frac{2N}{N-2}$ is the Sobolev critical exponent. If ![]() $\bar{p} \lt p \lt 2^{*}$, then
$\bar{p} \lt p \lt 2^{*}$, then ![]() $C_{N,p}$ is the best constant in the Gagliardo–Nirenberg inequality [Reference Weinstein43]. If
$C_{N,p}$ is the best constant in the Gagliardo–Nirenberg inequality [Reference Weinstein43]. If ![]() $p=2^{*}$, then
$p=2^{*}$, then ![]() $C_{N,p}$ is the optimal constant in the Sobolev inequality [Reference Talenti38]. Then the following holds:
$C_{N,p}$ is the optimal constant in the Sobolev inequality [Reference Talenti38]. Then the following holds:
(i) ![]() $I(u)|_{\widetilde{S}}(a)$ has a critical point
$I(u)|_{\widetilde{S}}(a)$ has a critical point ![]() $\widehat{u}\in W^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ at level
$\widehat{u}\in W^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ at level ![]() $m(a,\tau) \lt 0$ which is an interior minimizer of I(u) on the set:
$m(a,\tau) \lt 0$ which is an interior minimizer of I(u) on the set:
 \begin{equation*}A_{k}:=\{u\in {\widetilde{S}}(a): |\nabla u|_{2}^{2} \lt k\},\end{equation*}
\begin{equation*}A_{k}:=\{u\in {\widetilde{S}}(a): |\nabla u|_{2}^{2} \lt k\},\end{equation*} for a suitable k > 0 small enough. Moreover, ![]() $\widehat{u}$ is a ground state normalized solution to (1.1).
$\widehat{u}$ is a ground state normalized solution to (1.1).
(ii) ![]() $I(u)|_{\widetilde{S}}(a)$ has a second critical point of mountain-pass type
$I(u)|_{\widetilde{S}}(a)$ has a second critical point of mountain-pass type ![]() $\overline{u}\in W^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ at level
$\overline{u}\in W^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ at level ![]() $\sigma(a,\tau) \gt 0$.
$\sigma(a,\tau) \gt 0$.
(iii) Both ![]() $\widehat{u}$ and
$\widehat{u}$ and ![]() $\overline{u}$ are radially symmetric positive functions.
$\overline{u}$ are radially symmetric positive functions.
Remark 1.1. It’s well known that quasilinear Schrödinger equation (1.1) is in contrast with semilinear Schrödinger equation [Reference Ambrosetti, Badiale and Cingolani3, Reference Barstch and Wang7, Reference Barstch, Wang, Willem and Quittner8, Reference Rabinowitz32, Reference Soave36, Reference Soave37, Reference Tang39–Reference Tarantello41, Reference Zhang and Zhao46]. (1.1) becomes much more complicated due to the existence of the term ![]() $u\Delta u^{2}$ which implies that the corresponding energy functional I(u) in case of
$u\Delta u^{2}$ which implies that the corresponding energy functional I(u) in case of ![]() $N\geq2$ is non-differentiable in Sobolev space
$N\geq2$ is non-differentiable in Sobolev space ![]() $\mathcal{H}$, in addition, the existence of the L 2-supercritical nonlinearities means the associated energy functional of (1.1) is unbounded from below on
$\mathcal{H}$, in addition, the existence of the L 2-supercritical nonlinearities means the associated energy functional of (1.1) is unbounded from below on  $\widetilde{S}(a)$ which prevents us using similar minimax variational argument to that used to semilinear Schrödinger equation. On the other hand, different from [Reference Li and Zou23] which studied the quasilinear equations in form of (1.1) with pure L 2-supercritical homogeneous nonlinearity
$\widetilde{S}(a)$ which prevents us using similar minimax variational argument to that used to semilinear Schrödinger equation. On the other hand, different from [Reference Li and Zou23] which studied the quasilinear equations in form of (1.1) with pure L 2-supercritical homogeneous nonlinearity ![]() $|u|^{p-2}u$, we here consider the combination case of L 2-subcritical and L 2-supercritical nonlinearities which forces us to find an ingenious function space which is smaller than the Pohozaev manifold on which we analyse the geometry of the energy functional and prove the multiplicity and properties of normalized solutions. Our work extends and develops some recent results in the literature.
$|u|^{p-2}u$, we here consider the combination case of L 2-subcritical and L 2-supercritical nonlinearities which forces us to find an ingenious function space which is smaller than the Pohozaev manifold on which we analyse the geometry of the energy functional and prove the multiplicity and properties of normalized solutions. Our work extends and develops some recent results in the literature.
Our proof is based on variational methods. Due to the existence of ![]() $u\Delta u^{2}$ and L 2-supercritical nonlinearities, the associated energy functional of (1.1) is non-smooth and unbounded from below on
$u\Delta u^{2}$ and L 2-supercritical nonlinearities, the associated energy functional of (1.1) is non-smooth and unbounded from below on  $\widetilde{S}(a)$. To get over this problem, we adopt perturbation methods and need to find appropriate condition and Pohozaev manifold which is a smaller function space and a natural constraint in
$\widetilde{S}(a)$. To get over this problem, we adopt perturbation methods and need to find appropriate condition and Pohozaev manifold which is a smaller function space and a natural constraint in  $\widetilde{S}(a)$ in which one may find some critical points of the energy functional. But for the combination of L 2-subcritical and L 2-supercritical nonlinearities, note that the interplay strongly affects the geometry of the energy functional, hence we need to not only find a certain subset of
$\widetilde{S}(a)$ in which one may find some critical points of the energy functional. But for the combination of L 2-subcritical and L 2-supercritical nonlinearities, note that the interplay strongly affects the geometry of the energy functional, hence we need to not only find a certain subset of ![]() $\mathbb{R}^{2}$ to which parameters pair (p, q) belongs but also build an ingenious function space which is smaller than the Pohozaev manifold (see (2.1) for more details) in order to prove the multiplicity and properties of normalized solutions. And we also need a additional condition, see (1.10). It’s worth noting that the dimensions in Theorems 1.1 and 1.2 are limited due to an important lemma which is used to control the Lagrange multipliers, see Lemma 2.2 for more details.
$\mathbb{R}^{2}$ to which parameters pair (p, q) belongs but also build an ingenious function space which is smaller than the Pohozaev manifold (see (2.1) for more details) in order to prove the multiplicity and properties of normalized solutions. And we also need a additional condition, see (1.10). It’s worth noting that the dimensions in Theorems 1.1 and 1.2 are limited due to an important lemma which is used to control the Lagrange multipliers, see Lemma 2.2 for more details.
The remainder of this paper is organized as follows. In ![]() $\S$ 2 we give the perturbation setting and collect some important preliminaries. Section 3 is devoted to give the proof of the compactness of P.S. sequences for
$\S$ 2 we give the perturbation setting and collect some important preliminaries. Section 3 is devoted to give the proof of the compactness of P.S. sequences for ![]() $I_{\mu}|_{S(a)}$. In
$I_{\mu}|_{S(a)}$. In ![]() $\S$ 4 we will consider the critical points of
$\S$ 4 we will consider the critical points of ![]() $I_{\mu}|_{S(a)}$ in Theorem 1.1. Section 5 is devoted to study the critical points of
$I_{\mu}|_{S(a)}$ in Theorem 1.1. Section 5 is devoted to study the critical points of ![]() $I_{\mu}|_{S(a)}$ in Theorem 1.2. Finally, in
$I_{\mu}|_{S(a)}$ in Theorem 1.2. Finally, in ![]() $\S$ 6 we give the proofs of Theorems 1.1 and 1.2.
$\S$ 6 we give the proofs of Theorems 1.1 and 1.2.
Regarding the notation, in this paper, the notation ![]() $|\cdot|_{p}$ denotes the L p-norm. The symbols
$|\cdot|_{p}$ denotes the L p-norm. The symbols ![]() $\rightharpoonup$ and
$\rightharpoonup$ and ![]() $\rightarrow$ denote weak convergence and strong convergence respectively. Capital latter C and K stand for positive constants which may depend on some parameters, whose precise value can change from line to line.
$\rightarrow$ denote weak convergence and strong convergence respectively. Capital latter C and K stand for positive constants which may depend on some parameters, whose precise value can change from line to line.
2. Preliminaries
2.1. Perturbation setting
Let I(u) be defined by (1.5). It is not difficult to show that the I(u) is of class C 1 in ![]() $W^{1,2}(\mathbb{R}^{N})$ if and only if N = 1 due to the existence of the term
$W^{1,2}(\mathbb{R}^{N})$ if and only if N = 1 due to the existence of the term  $\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}$. In order to deal with the dimensions
$\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}$. In order to deal with the dimensions ![]() $N\geq 2$, we need to overcome the non-differentiability at first. And here a perturbation method is used to solve this difficulty. Then for
$N\geq 2$, we need to overcome the non-differentiability at first. And here a perturbation method is used to solve this difficulty. Then for ![]() $N\geq2$ and any
$N\geq2$ and any ![]() $\mu\in(0,1]$, we introduce a perturbation problem:
$\mu\in(0,1]$, we introduce a perturbation problem:
 \begin{equation*}I_{\mu}(u):=\frac{\mu}{\theta}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+I(u),\end{equation*}
\begin{equation*}I_{\mu}(u):=\frac{\mu}{\theta}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+I(u),\end{equation*}where θ satisfies:
 \begin{equation*}\frac{4N}{N+2} \lt \theta \lt \min\left\{\frac{4N+4}{N+2},N\right\} \ \ \ {\rm if}\ N\geq3, \end{equation*}
\begin{equation*}\frac{4N}{N+2} \lt \theta \lt \min\left\{\frac{4N+4}{N+2},N\right\} \ \ \ {\rm if}\ N\geq3, \end{equation*}and,
We consider the corresponding space ![]() $\mathcal{X}:=W^{1,\theta}(\mathbb{R}^{N})\cap W^{1,2}(\mathbb{R}^{N})$. Then
$\mathcal{X}:=W^{1,\theta}(\mathbb{R}^{N})\cap W^{1,2}(\mathbb{R}^{N})$. Then ![]() $\mathcal{X}$ is a reflexive Banach space. We get from Lemma A.1 [Reference Li and Zou23] that
$\mathcal{X}$ is a reflexive Banach space. We get from Lemma A.1 [Reference Li and Zou23] that ![]() $I_{\mu}\in C^{1}(\mathcal{X})$. To find some critical points of
$I_{\mu}\in C^{1}(\mathcal{X})$. To find some critical points of ![]() $I_{\mu}|_{S(a)}$, where
$I_{\mu}|_{S(a)}$, where
 \begin{equation*}S(a):=\left\{u\in\mathcal{X}: \int_{\mathbb{R}^{N}}|u|^{2}=a^{2}\right\},\end{equation*}
\begin{equation*}S(a):=\left\{u\in\mathcal{X}: \int_{\mathbb{R}^{N}}|u|^{2}=a^{2}\right\},\end{equation*}we can recall the L 2-norm preserved transform [Reference Jeanjean18]:
 \begin{equation*}u\in S(a)\mapsto s*u(x)=e^{\frac{N}{2}s}u(e^{s}x)\in S(a).\end{equation*}
\begin{equation*}u\in S(a)\mapsto s*u(x)=e^{\frac{N}{2}s}u(e^{s}x)\in S(a).\end{equation*}And, we will study the fiber maps:
 \begin{align*}\Psi_{\mu}(s):=&I_{\mu}(s*u)\\
& =\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad -e^{-Ns}\int_{\mathbb{R}^{N}}F(e^{\frac{N}{2}s}u).
\end{align*}
\begin{align*}\Psi_{\mu}(s):=&I_{\mu}(s*u)\\
& =\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad -e^{-Ns}\int_{\mathbb{R}^{N}}F(e^{\frac{N}{2}s}u).
\end{align*}Define
 \begin{align*}Q_{\mu}(u):=&\frac{d}{ds}|_{s=0}I_{\mu}(s*u)\\
=&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad -\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)]\\
=&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}-N\int_{\mathbb{R}^{N}}\widetilde{F}(u).
\end{align*}
\begin{align*}Q_{\mu}(u):=&\frac{d}{ds}|_{s=0}I_{\mu}(s*u)\\
=&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad -\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)]\\
=&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}-N\int_{\mathbb{R}^{N}}\widetilde{F}(u).
\end{align*} Then, ![]() $Q_{\mu}\in C^{1}(\mathcal{X})$, see Lemma A.1 in [Reference Li and Zou23] for more details. We also define the Pohozaev manifold:
$Q_{\mu}\in C^{1}(\mathcal{X})$, see Lemma A.1 in [Reference Li and Zou23] for more details. We also define the Pohozaev manifold:
then we observed that critical points of ![]() $I_{\mu}(u)|_{S(a)}$ allow to project a function on
$I_{\mu}(u)|_{S(a)}$ allow to project a function on ![]() $\mathcal{Q}_{\mu}(a)$. In this direction, we will study the decomposition of
$\mathcal{Q}_{\mu}(a)$. In this direction, we will study the decomposition of ![]() $\mathcal{Q}_{\mu}(a)$ into the disjoint union:
$\mathcal{Q}_{\mu}(a)$ into the disjoint union:
 \begin{equation*}\mathcal{Q}_{\mu}(a)=\mathcal{Q}_{\mu}^{+}(a)\cup\mathcal{Q}_{\mu}^{0}(a)\cup\mathcal{Q}_{\mu}^{-}(a),\end{equation*}
\begin{equation*}\mathcal{Q}_{\mu}(a)=\mathcal{Q}_{\mu}^{+}(a)\cup\mathcal{Q}_{\mu}^{0}(a)\cup\mathcal{Q}_{\mu}^{-}(a),\end{equation*}where
 \begin{equation*}\mathcal{Q}_{\mu}^{+}(a):=\left\{u\in \mathcal{Q}_{\mu}(a): \Psi_{\mu}''(0) \gt 0\right\},\end{equation*}
\begin{equation*}\mathcal{Q}_{\mu}^{+}(a):=\left\{u\in \mathcal{Q}_{\mu}(a): \Psi_{\mu}''(0) \gt 0\right\},\end{equation*} \begin{equation}
\mathcal{Q}_{\mu}^{0}(a):=\left\{u\in \mathcal{Q}_{\mu}(a): \Psi_{\mu}''(0)=0\right\},
\end{equation}
\begin{equation}
\mathcal{Q}_{\mu}^{0}(a):=\left\{u\in \mathcal{Q}_{\mu}(a): \Psi_{\mu}''(0)=0\right\},
\end{equation} \begin{equation*}\mathcal{Q}_{\mu}^{-}(a):=\left\{u\in \mathcal{Q}_{\mu}(a): \Psi_{\mu}''(0) \lt 0\right\}.\end{equation*}
\begin{equation*}\mathcal{Q}_{\mu}^{-}(a):=\left\{u\in \mathcal{Q}_{\mu}(a): \Psi_{\mu}''(0) \lt 0\right\}.\end{equation*}Proposition 2.1. Let ![]() $u\in S(a)$. Then
$u\in S(a)$. Then ![]() $s\in\mathbb{R}$ is a critical point of
$s\in\mathbb{R}$ is a critical point of ![]() $\Psi_{\mu}(s)$ if and only if
$\Psi_{\mu}(s)$ if and only if ![]() $s*u\in\mathcal{Q}_{\mu}(a)$.
$s*u\in\mathcal{Q}_{\mu}(a)$.
Proof. For ![]() $u\in S(a)$ and
$u\in S(a)$ and ![]() $s\in \mathbb{R}$, we get:
$s\in \mathbb{R}$, we get:
 \begin{equation*}\begin{aligned}\Psi_{\mu}'(s)=&(1+\gamma_{\theta})\mu e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{2s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\frac{N}{2}e^{-Ns}\int_{\mathbb{R}^{N}}\left[f(e^{\frac{N}{2}s}u)u-2F(e^{\frac{N}{2}s}u)\right]\\
=&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla (s*u)|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla (s*u)|^{2}+(2+N)\int_{\mathbb{R}^{N}}|s*u|^{2}|\nabla (s*u)|^{2}\\
&-\frac{N}{2}\int_{\mathbb{R}^{N}}\left[f(s*u)(s*u)-2F(s*u)\right]=Q_{\mu}(s*u).
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}\Psi_{\mu}'(s)=&(1+\gamma_{\theta})\mu e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{2s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\frac{N}{2}e^{-Ns}\int_{\mathbb{R}^{N}}\left[f(e^{\frac{N}{2}s}u)u-2F(e^{\frac{N}{2}s}u)\right]\\
=&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla (s*u)|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla (s*u)|^{2}+(2+N)\int_{\mathbb{R}^{N}}|s*u|^{2}|\nabla (s*u)|^{2}\\
&-\frac{N}{2}\int_{\mathbb{R}^{N}}\left[f(s*u)(s*u)-2F(s*u)\right]=Q_{\mu}(s*u).
\end{aligned}
\end{equation*} Therefore, ![]() $s\in\mathbb{R}$ is a critical point of
$s\in\mathbb{R}$ is a critical point of ![]() $\Psi_{\mu}(s)$ if and only if
$\Psi_{\mu}(s)$ if and only if ![]() $s*u\in\mathcal{Q}_{\mu}(a)$.
$s*u\in\mathcal{Q}_{\mu}(a)$.
In particular, ![]() $u\in\mathcal{Q}_{\mu}(a)$ if and only if 0 is a critical point of
$u\in\mathcal{Q}_{\mu}(a)$ if and only if 0 is a critical point of ![]() $\Psi_{\mu}(s)$. By Lemma 3.5 in [Reference Barstch and Soave6], the map
$\Psi_{\mu}(s)$. By Lemma 3.5 in [Reference Barstch and Soave6], the map ![]() $(s,u)\in\mathbb{R}\times \mathcal{X}\mapsto s*u\in\mathcal{X}$ is continuous.
$(s,u)\in\mathbb{R}\times \mathcal{X}\mapsto s*u\in\mathcal{X}$ is continuous.
2.2. An essential lemma
The following lemma is used to control the values of the corresponding Lagrange multipliers in this paper.
Lemma 2.2. For any ![]() $0\leq\mu\leq1$, assume that u ≠ 0 is a critical of
$0\leq\mu\leq1$, assume that u ≠ 0 is a critical of ![]() $I_{\mu}|_{S(a)}$, it follows that there exists a
$I_{\mu}|_{S(a)}$, it follows that there exists a ![]() $\lambda\in\mathbb{R}$, such that
$\lambda\in\mathbb{R}$, such that
 \begin{equation*}I_{\mu}'(u)+\lambda u=0.\end{equation*}
\begin{equation*}I_{\mu}'(u)+\lambda u=0.\end{equation*}Suppose that one of the following conditions holds:
(a) f(u) satisfies (F1) and (F2), a > 0.
(b) ![]() $f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2), a > 0.
$f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2), a > 0.
Then λ > 0.
Proof. For the case (a), by applying ![]() $Q_{\mu}(u)=0$ and (1.1), we get
$Q_{\mu}(u)=0$ and (1.1), we get
 \begin{align*}\lambda a^{2}=&\mu\left(\frac{2(1+\gamma_{\theta})}{N}-1\right)\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}\\
&+\left(\frac{2}{N}-1\right)\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\left[\frac{2(2+N)}{N}-4\right]\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
+2\int_{\mathbb{R}^{N}}F(u).
\end{align*}
\begin{align*}\lambda a^{2}=&\mu\left(\frac{2(1+\gamma_{\theta})}{N}-1\right)\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}\\
&+\left(\frac{2}{N}-1\right)\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\left[\frac{2(2+N)}{N}-4\right]\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
+2\int_{\mathbb{R}^{N}}F(u).
\end{align*} So if condition (a) holds, in the sense that ![]() $N\leq2$, then we have λ > 0.
$N\leq2$, then we have λ > 0.
For the case (b), combining ![]() $Q_{\mu}(u)=0$ with (1.1), we have:
$Q_{\mu}(u)=0$ with (1.1), we have:
 \begin{align*}\lambda\gamma_{p}a^{2}=
&\mu(1+\gamma_{\theta}-\gamma_{p})\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}\\
&+(1-\gamma_{p})\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N-4\gamma_{p})\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
+\tau(\gamma_{p}-\gamma_{q})\int_{\mathbb{R}^{N}}|u|^{q}\\
=&\mu(1+\frac{N(\theta-p)}{\theta p})\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}\\
&+\frac{2N-(N-2)p}{2p}\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+\frac{4N-(N-2)p}{p}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
& \qquad\qquad +\tau(\gamma_{p}-\gamma_{q})\int_{\mathbb{R}^{N}}|u|^{q}.
\end{align*}
\begin{align*}\lambda\gamma_{p}a^{2}=
&\mu(1+\gamma_{\theta}-\gamma_{p})\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}\\
&+(1-\gamma_{p})\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N-4\gamma_{p})\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
+\tau(\gamma_{p}-\gamma_{q})\int_{\mathbb{R}^{N}}|u|^{q}\\
=&\mu(1+\frac{N(\theta-p)}{\theta p})\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}\\
&+\frac{2N-(N-2)p}{2p}\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+\frac{4N-(N-2)p}{p}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
& \qquad\qquad +\tau(\gamma_{p}-\gamma_{q})\int_{\mathbb{R}^{N}}|u|^{q}.
\end{align*}So if condition (b) holds, we immediately get λ > 0.
3. The compactness of P.S. sequence of  $I_{\mu}|_{S(a)}$
$I_{\mu}|_{S(a)}$
Lemma 3.1. Let ![]() $0 \lt \mu\leq1$,
$0 \lt \mu\leq1$, ![]() $N\geq2$, assume that one of the following conditions holds
$N\geq2$, assume that one of the following conditions holds
(a) f(u) satisfies (F1) and (F2).
(b) ![]() $f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2).
$f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2).
Let ![]() $\{u_{n}\}\subset S_{r}(a)$ be a P.S. sequence for
$\{u_{n}\}\subset S_{r}(a)$ be a P.S. sequence for ![]() $I_{\mu}|_{S(a)}$ at level c ≠ 0, and assume in addition that
$I_{\mu}|_{S(a)}$ at level c ≠ 0, and assume in addition that ![]() $Q_{\mu}(u_{n})\rightarrow0$ as
$Q_{\mu}(u_{n})\rightarrow0$ as ![]() $n\rightarrow\infty$. Then up to a subsequence
$n\rightarrow\infty$. Then up to a subsequence
 \begin{equation*}u_{n}\rightharpoonup u_{\mu} \ {\rm in}\ \mathcal{X} \ \ \ {\rm and}\ \ \
I_{\mu}'(u_{\mu})+\lambda_{\mu} u_{\mu}=0.\end{equation*}
\begin{equation*}u_{n}\rightharpoonup u_{\mu} \ {\rm in}\ \mathcal{X} \ \ \ {\rm and}\ \ \
I_{\mu}'(u_{\mu})+\lambda_{\mu} u_{\mu}=0.\end{equation*} Moreover, if ![]() $\lambda_{\mu}\neq0$, we have that:
$\lambda_{\mu}\neq0$, we have that:
Proof. The proof is divided into three steps.
Step 1. ![]() $\{u_{n}\}$ is bounded in
$\{u_{n}\}$ is bounded in ![]() $\mathcal{X}_{r}$.
$\mathcal{X}_{r}$.
We consider the case that f(u) satisfies (F1) and (F2) at first. Since ![]() $Q_{\mu}(u_{n})\rightarrow0$, it shows that:
$Q_{\mu}(u_{n})\rightarrow0$, it shows that:
 \begin{equation*}\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}\\
&-\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{n})u_{n}-2F(u_{n})]=o(1)\ \ \ \ {\rm as}\ n\rightarrow\infty.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}\\
&-\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{n})u_{n}-2F(u_{n})]=o(1)\ \ \ \ {\rm as}\ n\rightarrow\infty.
\end{aligned}
\end{equation*} We deduce from (F1) that ![]() $(\alpha-2)F(u)\leq f(u)u-2F(u)\leq(\beta-2)F(u)$, then
$(\alpha-2)F(u)\leq f(u)u-2F(u)\leq(\beta-2)F(u)$, then  $\widetilde{Q}_{\mu}(u_{n})\geq o(1)$, where
$\widetilde{Q}_{\mu}(u_{n})\geq o(1)$, where
 \begin{equation*}\widetilde{Q}_{\mu}(u_{n}):
=(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}
-\alpha\gamma_{\alpha}\int_{\mathbb{R}^{N}}F(u_{n}).\end{equation*}
\begin{equation*}\widetilde{Q}_{\mu}(u_{n}):
=(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}
-\alpha\gamma_{\alpha}\int_{\mathbb{R}^{N}}F(u_{n}).\end{equation*} Thus, for ![]() $\{u_{n}\}\subset S_{r}(a)$ with
$\{u_{n}\}\subset S_{r}(a)$ with ![]() $Q_{\mu}(u_{n})\rightarrow0$, there holds:
$Q_{\mu}(u_{n})\rightarrow0$, there holds:
 \begin{align*}I_{\mu}(u_{n})
&\geq I_{\mu}(u_{n})-\frac{1}{\alpha\gamma_{\alpha}}\widetilde{Q}_{\mu}(u_{n})\\
&=\frac{\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta}}{\theta\alpha\gamma_{\alpha}}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}
+\frac{\alpha\gamma_{\alpha}-2}{2\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\\
& \qquad\qquad +\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}+o(1).
\end{align*}
\begin{align*}I_{\mu}(u_{n})
&\geq I_{\mu}(u_{n})-\frac{1}{\alpha\gamma_{\alpha}}\widetilde{Q}_{\mu}(u_{n})\\
&=\frac{\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta}}{\theta\alpha\gamma_{\alpha}}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}
+\frac{\alpha\gamma_{\alpha}-2}{2\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\\
& \qquad\qquad +\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}+o(1).
\end{align*} Since ![]() $\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta} \gt 0$,
$\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta} \gt 0$, ![]() $\alpha\gamma_{\alpha}-2 \gt 0$,
$\alpha\gamma_{\alpha}-2 \gt 0$, ![]() $\alpha\gamma_{\alpha}-2-N \gt 0$ and
$\alpha\gamma_{\alpha}-2-N \gt 0$ and ![]() $I_{\mu}(u_{n})\rightarrow c \lt +\infty$, then there exists a constant
$I_{\mu}(u_{n})\rightarrow c \lt +\infty$, then there exists a constant ![]() $C_{1} \gt 0$ such that:
$C_{1} \gt 0$ such that:
 \begin{equation*}\sup\limits_{n\geq1}\max\left\{\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta},\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2},\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2} \right\}\leq C_{1} \lt +\infty,\end{equation*}
\begin{equation*}\sup\limits_{n\geq1}\max\left\{\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta},\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2},\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2} \right\}\leq C_{1} \lt +\infty,\end{equation*} this implies ![]() $\{u_{n}\}$ is bounded in
$\{u_{n}\}$ is bounded in ![]() $\mathcal{X}_{r}$.
$\mathcal{X}_{r}$.
If ![]() $f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2), then by
$f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2), then by ![]() $Q_{\mu}(u_{n})\rightarrow0$ and the Gagliardo–Nirenberg inequality, we have:
$Q_{\mu}(u_{n})\rightarrow0$ and the Gagliardo–Nirenberg inequality, we have:
 \begin{align*}
I_{\mu}(u_{n})=&I_{\mu}(u_{n})-\frac{1}{p\gamma_{p}}Q_{\mu}(u_{n})\\
=&\frac{p\gamma_{p}-\theta-\theta\gamma_{\theta}}{\theta p\gamma_{p}}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}
+\frac{p\gamma_{p}-2}{2p\gamma_{p}}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\\
& \quad+\frac{p\gamma_{p}-2-N}{p\gamma_{p}}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}
-\frac{\tau(p\gamma_{p}-q\gamma_{q})}{qp\gamma_{p}}\int_{\mathbb{R}^{N}}|u_{n}|^{q}+o(1)\\
\geq&\frac{p\gamma_{p}-\theta-\theta\gamma_{\theta}}{\theta p\gamma_{p}}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}
+\frac{p\gamma_{p}-2}{2p\gamma_{p}}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\\
& \quad+\frac{p\gamma_{p}-2-N}{p\gamma_{p}}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2} -\frac{\tau(p\gamma_{p}-q\gamma_{q})}{qp\gamma_{p}}C_{N,q}^{q}a^{(1-\gamma_{q})q}|\nabla u_{n}|_{2}^{q\gamma_{q}}+o(1).
\end{align*}
\begin{align*}
I_{\mu}(u_{n})=&I_{\mu}(u_{n})-\frac{1}{p\gamma_{p}}Q_{\mu}(u_{n})\\
=&\frac{p\gamma_{p}-\theta-\theta\gamma_{\theta}}{\theta p\gamma_{p}}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}
+\frac{p\gamma_{p}-2}{2p\gamma_{p}}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\\
& \quad+\frac{p\gamma_{p}-2-N}{p\gamma_{p}}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}
-\frac{\tau(p\gamma_{p}-q\gamma_{q})}{qp\gamma_{p}}\int_{\mathbb{R}^{N}}|u_{n}|^{q}+o(1)\\
\geq&\frac{p\gamma_{p}-\theta-\theta\gamma_{\theta}}{\theta p\gamma_{p}}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}
+\frac{p\gamma_{p}-2}{2p\gamma_{p}}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\\
& \quad+\frac{p\gamma_{p}-2-N}{p\gamma_{p}}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2} -\frac{\tau(p\gamma_{p}-q\gamma_{q})}{qp\gamma_{p}}C_{N,q}^{q}a^{(1-\gamma_{q})q}|\nabla u_{n}|_{2}^{q\gamma_{q}}+o(1).
\end{align*} Since ![]() $I_{\mu}(u_{n})\rightarrow c \lt +\infty$ as
$I_{\mu}(u_{n})\rightarrow c \lt +\infty$ as ![]() $n\rightarrow\infty$, then there exists a constant
$n\rightarrow\infty$, then there exists a constant ![]() $C_{2} \gt 0$ such that:
$C_{2} \gt 0$ such that:
 \begin{equation*}\frac{p\gamma_{p}-2}{2p\gamma_{p}}|\nabla u_{n}|_{2}^{2}
-\frac{\tau(p\gamma_{p}-q\gamma_{q})}{qp\gamma_{p}}C_{N,q}^{q}a^{(1-\gamma_{q})q}|\nabla u_{n}|_{2}^{q\gamma_{q}}\leq C_{2}.\end{equation*}
\begin{equation*}\frac{p\gamma_{p}-2}{2p\gamma_{p}}|\nabla u_{n}|_{2}^{2}
-\frac{\tau(p\gamma_{p}-q\gamma_{q})}{qp\gamma_{p}}C_{N,q}^{q}a^{(1-\gamma_{q})q}|\nabla u_{n}|_{2}^{q\gamma_{q}}\leq C_{2}.\end{equation*} Since ![]() $q\gamma_{q} \lt 2$, then there exists
$q\gamma_{q} \lt 2$, then there exists ![]() $C_{3} \gt 0$ such that for every
$C_{3} \gt 0$ such that for every ![]() $n\geq1$, we have
$n\geq1$, we have ![]() $|\nabla u_{n}|_{2}\leq C_{3}$. Recalling that
$|\nabla u_{n}|_{2}\leq C_{3}$. Recalling that ![]() $I_{\mu}(u_{n})\rightarrow c \lt +\infty$ as
$I_{\mu}(u_{n})\rightarrow c \lt +\infty$ as ![]() $n\rightarrow\infty$, we deduce that there exists a constant
$n\rightarrow\infty$, we deduce that there exists a constant ![]() $C_{4} \gt 0$ such that:
$C_{4} \gt 0$ such that:
 \begin{equation*}\sup\limits_{n\geq1}\max\left\{\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta},\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2},\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2} \right\}\leq C_{4} \lt +\infty,\end{equation*}
\begin{equation*}\sup\limits_{n\geq1}\max\left\{\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta},\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2},\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2} \right\}\leq C_{4} \lt +\infty,\end{equation*} it shows that ![]() $\{u_{n}\}$ is bounded in
$\{u_{n}\}$ is bounded in ![]() $\mathcal{X}_{r}$.
$\mathcal{X}_{r}$.
Step 2. ![]() $\{\lambda_{n}\}$ is bounded.
$\{\lambda_{n}\}$ is bounded.
Since ![]() $N\geq2$, the embedding
$N\geq2$, the embedding ![]() $\mathcal{X}_{r}\hookrightarrow L^{r}(\mathbb{R}^{N})$ is compact for
$\mathcal{X}_{r}\hookrightarrow L^{r}(\mathbb{R}^{N})$ is compact for ![]() $r\in(2,2^{*})$. We deduce from the boundedness of the P.S. sequence
$r\in(2,2^{*})$. We deduce from the boundedness of the P.S. sequence ![]() $\{u_{n}\}$ that, up to a subsequence, there exists a
$\{u_{n}\}$ that, up to a subsequence, there exists a ![]() $u_{\mu}\in \mathcal{X}_{r}$ such that:
$u_{\mu}\in \mathcal{X}_{r}$ such that:
 \begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm in} \ \mathcal{X} \ {\rm and}\ {\rm in}\ L^{2}(\mathbb{R}^{N}),\end{equation*}
\begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm in} \ \mathcal{X} \ {\rm and}\ {\rm in}\ L^{2}(\mathbb{R}^{N}),\end{equation*} \begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm in}\ L^{r}(\mathbb{R}^{N}),\ \forall r \in(2,2^{*}),\end{equation*}
\begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm in}\ L^{r}(\mathbb{R}^{N}),\ \forall r \in(2,2^{*}),\end{equation*} \begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm a.e.}\ {\rm on}\ \mathbb{R}^{N}.\end{equation*}
\begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm a.e.}\ {\rm on}\ \mathbb{R}^{N}.\end{equation*}Combining interpolation with the inequality (1.6), we have that:
 \begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm in}\ L^{r}(\mathbb{R}^{N}),\ \forall r \in(2,2\cdot2^{*}).\end{equation*}
\begin{equation*}u_{n}\rightarrow u_{\mu}\ \ \ {\rm in}\ L^{r}(\mathbb{R}^{N}),\ \forall r \in(2,2\cdot2^{*}).\end{equation*}Thus, if f(u) satisfies (a) or (b), we have:
 \begin{equation*}\int_{\mathbb{R}^{N}}f(u_{n})u_{n}\rightarrow\int_{\mathbb{R}^{N}}f(u_{\mu})u_{\mu}\quad {\rm and} \quad int_{\mathbb{R}^{N}}F(u_{n})\rightarrow\int_{\mathbb{R}^{N}}F(u_{\mu}).\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{N}}f(u_{n})u_{n}\rightarrow\int_{\mathbb{R}^{N}}f(u_{\mu})u_{\mu}\quad {\rm and} \quad int_{\mathbb{R}^{N}}F(u_{n})\rightarrow\int_{\mathbb{R}^{N}}F(u_{\mu}).\end{equation*} We claim that ![]() $u_{\mu}\neq0$. Suppose that
$u_{\mu}\neq0$. Suppose that ![]() $u_{\mu}=0$, then as
$u_{\mu}=0$, then as ![]() $n\rightarrow\infty$:
$n\rightarrow\infty$:
 \begin{equation*}\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}\\
&=Q_{\mu}(u_{n})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{n})u_{n}-2F(u_{n})]\rightarrow0,
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}\\
&=Q_{\mu}(u_{n})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{n})u_{n}-2F(u_{n})]\rightarrow0,
\end{aligned}
\end{equation*} which implies that ![]() $I_{\mu}(u_{n})\rightarrow0$, in contradiction with
$I_{\mu}(u_{n})\rightarrow0$, in contradiction with ![]() $I_{\mu}(u_{n})\rightarrow c\neq0$. So
$I_{\mu}(u_{n})\rightarrow c\neq0$. So ![]() $u_{\mu}\neq0$. By Lemma 3 in [Reference Berestycki and Lions9], it follows from
$u_{\mu}\neq0$. By Lemma 3 in [Reference Berestycki and Lions9], it follows from  $I_{\mu}|_{S(a)}'(u_{n})\rightarrow0$ that there exists a sequence
$I_{\mu}|_{S(a)}'(u_{n})\rightarrow0$ that there exists a sequence ![]() $\lambda_{n}\in\mathbb{R}$ such that:
$\lambda_{n}\in\mathbb{R}$ such that:
 \begin{equation}
I_{\mu}'(u_{n})+\lambda_{n} u_{n}=0\ \ \ {\rm in}\ \mathcal{X}^{*}.
\end{equation}
\begin{equation}
I_{\mu}'(u_{n})+\lambda_{n} u_{n}=0\ \ \ {\rm in}\ \mathcal{X}^{*}.
\end{equation} Hence  $\lambda_{n}=-\frac{1}{a^{2}}I_{\mu}'(u_{n})[u_{n}]+o_{n}(1)$ is bounded in
$\lambda_{n}=-\frac{1}{a^{2}}I_{\mu}'(u_{n})[u_{n}]+o_{n}(1)$ is bounded in ![]() $\mathbb{R}$, and up to a subsequence, there exists a
$\mathbb{R}$, and up to a subsequence, there exists a ![]() $\lambda_{\mu}\in \mathbb{R}$, such that
$\lambda_{\mu}\in \mathbb{R}$, such that ![]() $\lambda_{n}\rightarrow \lambda_{\mu}$.
$\lambda_{n}\rightarrow \lambda_{\mu}$.
Step 3. Conclusion.
By weak convergence, (3.1) shows that:
 \begin{equation}
I_{\mu}'(u_{\mu})+\lambda_{\mu} u_{\mu}=0\ \ \ {\rm in}\ \mathcal{X}^{*}.
\end{equation}
\begin{equation}
I_{\mu}'(u_{\mu})+\lambda_{\mu} u_{\mu}=0\ \ \ {\rm in}\ \mathcal{X}^{*}.
\end{equation} Then, testing (3.2) with ![]() $x\cdot\nabla u$ and u, we get
$x\cdot\nabla u$ and u, we get ![]() $Q_{\mu}(u_{\mu})=0$. That is,
$Q_{\mu}(u_{\mu})=0$. That is,
 \begin{equation*}Q_{\mu}(u_{n})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{n})u_{n}-2F(u_{n})]\rightarrow
Q_{\mu}(u_{\mu})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{\mu})u_{\mu}-2F(u_{\mu})].\end{equation*}
\begin{equation*}Q_{\mu}(u_{n})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{n})u_{n}-2F(u_{n})]\rightarrow
Q_{\mu}(u_{\mu})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{\mu})u_{\mu}-2F(u_{\mu})].\end{equation*}Then, combining the weak lower semi-continuous property, see Lemma 4.3 in [Reference Cingolani, Jeanjean and Squassina12], we have:
 \begin{equation*}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}\rightarrow\mu\int_{\mathbb{R}^{N}}|\nabla u_{\mu}|^{\theta},\end{equation*}
\begin{equation*}\mu\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{\theta}\rightarrow\mu\int_{\mathbb{R}^{N}}|\nabla u_{\mu}|^{\theta},\end{equation*} \begin{equation*}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|\nabla u_{\mu}|^{2},\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{N}}|\nabla u_{n}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|\nabla u_{\mu}|^{2},\end{equation*} \begin{equation*}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|u_{\mu}|^{2}|\nabla u_{\mu}|^{2}.\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{N}}|u_{n}|^{2}|\nabla u_{n}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|u_{\mu}|^{2}|\nabla u_{\mu}|^{2}.\end{equation*}Hence we get,
 \begin{equation}
I_{\mu}'(u_{n})[u_{n}]\rightarrow I_{\mu}'(u_{\mu})[u_{\mu}].
\end{equation}
\begin{equation}
I_{\mu}'(u_{n})[u_{n}]\rightarrow I_{\mu}'(u_{\mu})[u_{\mu}].
\end{equation} Combining with (3.1)-(3.3), there must be ![]() $\lambda_{n}|u_{n}|_{2}^{2}\rightarrow\lambda_{\mu}|u_{\mu}|_{2}^{2}$. So
$\lambda_{n}|u_{n}|_{2}^{2}\rightarrow\lambda_{\mu}|u_{\mu}|_{2}^{2}$. So ![]() $\lambda_{\mu}\neq0$ shows that
$\lambda_{\mu}\neq0$ shows that ![]() $u_{n}\rightarrow u_{\mu}$ in
$u_{n}\rightarrow u_{\mu}$ in ![]() $\mathcal{X}$.
$\mathcal{X}$.
In order to deal with the dimension N = 1, we need a variant of Lemma 3.1.
Lemma 3.2. Let ![]() $0 \lt \mu\leq1$,
$0 \lt \mu\leq1$, ![]() $N\geq1$, assume that one of the following conditions holds:
$N\geq1$, assume that one of the following conditions holds:
(a) f(u) satisfies (F1) and (F2).
(b) ![]() $f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2).
$f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2).
Let ![]() $\{u_{n}\}\subset S_{r}(a)$ be a P.S. sequence for
$\{u_{n}\}\subset S_{r}(a)$ be a P.S. sequence for ![]() $I_{\mu}|_{S(a)}$ at level c ≠ 0, and suppose in addition that:
$I_{\mu}|_{S(a)}$ at level c ≠ 0, and suppose in addition that:
(i) ![]() $Q_{\mu}(u_{n})\rightarrow0$ as
$Q_{\mu}(u_{n})\rightarrow0$ as ![]() $n\rightarrow\infty$.
$n\rightarrow\infty$.
(ii) There exists ![]() $\{v_{n}\}\subset S_{r}(a)$, with vn radially decreasing, such that
$\{v_{n}\}\subset S_{r}(a)$, with vn radially decreasing, such that ![]() $\|v_{n}-u_{n}\|\rightarrow0$ as
$\|v_{n}-u_{n}\|\rightarrow0$ as ![]() $n\rightarrow\infty$.
$n\rightarrow\infty$.
Then up to a subsequence
 \begin{equation*}u_{n}\rightharpoonup u_{\mu} \ {\rm in}\ \mathcal{X} \ \ \ {\rm and}\ \ \
I_{\mu}'(u_{\mu})+\lambda_{\mu} u_{\mu}=0.\end{equation*}
\begin{equation*}u_{n}\rightharpoonup u_{\mu} \ {\rm in}\ \mathcal{X} \ \ \ {\rm and}\ \ \
I_{\mu}'(u_{\mu})+\lambda_{\mu} u_{\mu}=0.\end{equation*} Moreover, if ![]() $\lambda_{\mu}\neq0$, we have that
$\lambda_{\mu}\neq0$, we have that
Proof. Similar to the proof of the Lemma 3.1, it is not difficult to modify the proof developed in dimensions ![]() $N\geq2$. For the case of N = 1,
$N\geq2$. For the case of N = 1, ![]() $\mathcal{X}_{r}$ does not embed compactly in
$\mathcal{X}_{r}$ does not embed compactly in ![]() $L^{r}(\mathbb{R}^{N})$. By Proposition 1.7.1 in [Reference Cazenave10], we see that the compactness holds for bounded sequence of radially decreasing functions. Here we omit the details.
$L^{r}(\mathbb{R}^{N})$. By Proposition 1.7.1 in [Reference Cazenave10], we see that the compactness holds for bounded sequence of radially decreasing functions. Here we omit the details.
4. The critical points of perturbed functional for Theorem 1.1
4.1. Properties of  $\mathcal{Q}_{\mu}(a)$
$\mathcal{Q}_{\mu}(a)$
Lemma 4.1. Let ![]() $0 \lt \mu\leq1$ and for any critical point of
$0 \lt \mu\leq1$ and for any critical point of ![]() $I_{\mu}|_{\mathcal{Q}_{\mu}(a)}$, if
$I_{\mu}|_{\mathcal{Q}_{\mu}(a)}$, if  $\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, then there exists
$\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, then there exists ![]() $\lambda\in\mathbb{R}$ such that:
$\lambda\in\mathbb{R}$ such that:
 \begin{equation*}I_{\mu}'(u)+\lambda u=0\ \ \ {\rm in}\ \mathcal{X}^{*}.\end{equation*}
\begin{equation*}I_{\mu}'(u)+\lambda u=0\ \ \ {\rm in}\ \mathcal{X}^{*}.\end{equation*}Proof. Let ![]() $0 \lt \mu\leq1$ and u is a critical point of
$0 \lt \mu\leq1$ and u is a critical point of ![]() $I_{\mu}|_{\mathcal{Q}_{\mu}(a)}$, then by the Lagrange multipliers rule there exist
$I_{\mu}|_{\mathcal{Q}_{\mu}(a)}$, then by the Lagrange multipliers rule there exist ![]() $\lambda,\ \nu\in\mathbb{R}$ such that:
$\lambda,\ \nu\in\mathbb{R}$ such that:
We only need to prove that ν = 0, to this end we get the Pohozaev identity:
 \begin{equation*}\Phi_{\mu}'(0)=\frac{d}{ds}\phi_{\mu}(s*u)|_{s=0}=0,\end{equation*}
\begin{equation*}\Phi_{\mu}'(0)=\frac{d}{ds}\phi_{\mu}(s*u)|_{s=0}=0,\end{equation*} where  $\phi_{\mu}(u):=I_{\mu}(u)+\frac{1}{2}\lambda|u|_{2}^{2}+\nu Q_{\mu}(u)$ is the corresponding energy functional to (4.1). Since
$\phi_{\mu}(u):=I_{\mu}(u)+\frac{1}{2}\lambda|u|_{2}^{2}+\nu Q_{\mu}(u)$ is the corresponding energy functional to (4.1). Since
 \begin{equation*}\Phi_{\mu}(s):=\phi_{\mu}(s*u)=I_{\mu}(s*u)+\frac{1}{2}\lambda|u|_{2}^{2}+\nu Q_{\mu}(s*u)
=\Psi_{\mu}(s)+\frac{1}{2}\lambda|u|_{2}^{2}+\nu\Psi_{\mu}'(s),\end{equation*}
\begin{equation*}\Phi_{\mu}(s):=\phi_{\mu}(s*u)=I_{\mu}(s*u)+\frac{1}{2}\lambda|u|_{2}^{2}+\nu Q_{\mu}(s*u)
=\Psi_{\mu}(s)+\frac{1}{2}\lambda|u|_{2}^{2}+\nu\Psi_{\mu}'(s),\end{equation*}then we have
 \begin{equation*}\Phi_{\mu}'(s):=\frac{d}{ds}\phi_{\mu}(s*u)
=\Psi_{\mu}'(s)+\nu \Psi_{\mu}''(s).\end{equation*}
\begin{equation*}\Phi_{\mu}'(s):=\frac{d}{ds}\phi_{\mu}(s*u)
=\Psi_{\mu}'(s)+\nu \Psi_{\mu}''(s).\end{equation*}Hence
 \begin{equation*}0=\Phi_{\mu}'(0)=(1+\nu)\Psi_{\mu}'(0)+\nu\Psi_{\mu}''(0)
=Q_{\mu}(u)+\nu\Psi_{\mu}''(0).\end{equation*}
\begin{equation*}0=\Phi_{\mu}'(0)=(1+\nu)\Psi_{\mu}'(0)+\nu\Psi_{\mu}''(0)
=Q_{\mu}(u)+\nu\Psi_{\mu}''(0).\end{equation*} Since  $\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, then
$\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, then ![]() $\Psi_{\mu}''(0)\neq0$, so ν = 0.
$\Psi_{\mu}''(0)\neq0$, so ν = 0.
Lemma 4.2. Under the assumption (F1),
 \begin{equation*}\mathcal{D}(a):=\inf\limits_{0 \lt \mu\leq1,u\in\mathcal{Q}_{\mu}(a)}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2} \gt 0,\end{equation*}
\begin{equation*}\mathcal{D}(a):=\inf\limits_{0 \lt \mu\leq1,u\in\mathcal{Q}_{\mu}(a)}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2} \gt 0,\end{equation*}is independent of µ.
Proof. For any ![]() $u\in\mathcal{Q}_{\mu}(a)$, we have:
$u\in\mathcal{Q}_{\mu}(a)$, we have:
 \begin{equation*}(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}-\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)]
=0,\end{equation*}
\begin{equation*}(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}-\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)]
=0,\end{equation*}then
 \begin{equation*}(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\leq\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)].\end{equation*}
\begin{equation*}(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\leq\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)].\end{equation*} We get from (F1) that ![]() $f(u)u-2F(u)\leq(\beta-2)F(u)$ and
$f(u)u-2F(u)\leq(\beta-2)F(u)$ and  $\int_{\mathbb{R}^{N}}F(u)\leq F(1)\int_{\mathbb{R}^{N}}\left(|u|^{\alpha}+|u|^{\beta}\right)$. By the inequality (1.6), there holds
$\int_{\mathbb{R}^{N}}F(u)\leq F(1)\int_{\mathbb{R}^{N}}\left(|u|^{\alpha}+|u|^{\beta}\right)$. By the inequality (1.6), there holds
 \begin{equation*}\begin{aligned}(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
\leq&\frac{N(\beta-2)}{2}F(1)\int_{\mathbb{R}^{N}}\left(|u|^{\alpha}+|u|^{\beta}\right)\\
\leq&\frac{N(\beta-2)}{2}F(1)K_{1}(\alpha,N)a^{\frac{4N-\alpha(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\alpha-2)}{2(N+2)}}\\
+&\frac{N(\beta-2)}{2}F(1)K_{2}(\beta,N)a^{\frac{4N-\beta(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\beta-2)}{2(N+2)}}.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
\leq&\frac{N(\beta-2)}{2}F(1)\int_{\mathbb{R}^{N}}\left(|u|^{\alpha}+|u|^{\beta}\right)\\
\leq&\frac{N(\beta-2)}{2}F(1)K_{1}(\alpha,N)a^{\frac{4N-\alpha(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\alpha-2)}{2(N+2)}}\\
+&\frac{N(\beta-2)}{2}F(1)K_{2}(\beta,N)a^{\frac{4N-\beta(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\beta-2)}{2(N+2)}}.
\end{aligned}
\end{equation*} Since  $\frac{N(\beta-2)}{2(N+2)} \gt \frac{N(\alpha-2)}{2(N+2)} \gt 1$, we have
$\frac{N(\beta-2)}{2(N+2)} \gt \frac{N(\alpha-2)}{2(N+2)} \gt 1$, we have ![]() $\mathcal{D}(a) \gt 0$.
$\mathcal{D}(a) \gt 0$.
Lemma 4.3. Let ![]() $0 \lt \mu\leq1$ and for any
$0 \lt \mu\leq1$ and for any ![]() $u\in\mathcal{Q}_{\mu}(a)$, if f(u) satisfies (F1) and (F2), then
$u\in\mathcal{Q}_{\mu}(a)$, if f(u) satisfies (F1) and (F2), then ![]() $\Psi_{\mu}''(0) \lt 0$ and
$\Psi_{\mu}''(0) \lt 0$ and ![]() $\mathcal{Q}_{\mu}(a)$ is a natural constraint of
$\mathcal{Q}_{\mu}(a)$ is a natural constraint of ![]() $I_{\mu}|_{S(a)}$.
$I_{\mu}|_{S(a)}$.
 \begin{align*}\Psi_{\mu}''(s)&=\theta(1+\gamma_{\theta})^{2}\mu e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+2e^{2s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
\qquad\qquad & +(2+N)^{2}e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\nonumber \\
&+N^{2}e^{-Ns}\int_{\mathbb{R}^{N}}\widetilde{F}(e^{\frac{N}{2}s}u)-\frac{N^{2}}{2}e^{-\frac{N}{2}s}\int_{\mathbb{R}^{N}}\widetilde{F}'(e^{\frac{N}{2}s}u)u.
\end{align*}
\begin{align*}\Psi_{\mu}''(s)&=\theta(1+\gamma_{\theta})^{2}\mu e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+2e^{2s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
\qquad\qquad & +(2+N)^{2}e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\nonumber \\
&+N^{2}e^{-Ns}\int_{\mathbb{R}^{N}}\widetilde{F}(e^{\frac{N}{2}s}u)-\frac{N^{2}}{2}e^{-\frac{N}{2}s}\int_{\mathbb{R}^{N}}\widetilde{F}'(e^{\frac{N}{2}s}u)u.
\end{align*}Thus
 \begin{equation*}\begin{aligned}
\Psi_{\mu}''(0)=&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&+N^{2}\int_{\mathbb{R}^{N}}\widetilde{F}(u)
-\frac{N^{2}}{2}\int_{\mathbb{R}^{N}}\widetilde{F}'(u)u.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
\Psi_{\mu}''(0)=&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&+N^{2}\int_{\mathbb{R}^{N}}\widetilde{F}(u)
-\frac{N^{2}}{2}\int_{\mathbb{R}^{N}}\widetilde{F}'(u)u.
\end{aligned}
\end{equation*} Then by the assumption ![]() $(F2)$ and
$(F2)$ and ![]() $Q_{\mu}(u)=0$,
$Q_{\mu}(u)=0$,
 \begin{equation*}\begin{aligned}
\Psi_{\mu}''(0)\leq&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&+N^{2}\int_{\mathbb{R}^{N}}\widetilde{F}(u)
-\frac{N^{2}}{2}\alpha\int_{\mathbb{R}^{N}}\widetilde{F}(u)\\
=&(1+\gamma_{\theta})\mu(\theta+\theta\gamma_{\theta}-\alpha\gamma_{\alpha})\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+(2-\alpha\gamma_{\alpha})\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
&+(2+N)(2+N-\alpha\gamma_{\alpha})\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
\Psi_{\mu}''(0)\leq&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&+N^{2}\int_{\mathbb{R}^{N}}\widetilde{F}(u)
-\frac{N^{2}}{2}\alpha\int_{\mathbb{R}^{N}}\widetilde{F}(u)\\
=&(1+\gamma_{\theta})\mu(\theta+\theta\gamma_{\theta}-\alpha\gamma_{\alpha})\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+(2-\alpha\gamma_{\alpha})\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
&+(2+N)(2+N-\alpha\gamma_{\alpha})\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}.
\end{aligned}
\end{equation*} Since ![]() $\alpha\gamma_{\alpha} \gt \theta+\theta\gamma_{\theta}$,
$\alpha\gamma_{\alpha} \gt \theta+\theta\gamma_{\theta}$, ![]() $\alpha\gamma_{\alpha} \gt 2$ and
$\alpha\gamma_{\alpha} \gt 2$ and ![]() $\alpha\gamma_{\alpha} \gt 2+N$ when
$\alpha\gamma_{\alpha} \gt 2+N$ when  $\alpha \gt 4+\frac{4}{N}$, then
$\alpha \gt 4+\frac{4}{N}$, then
 \begin{equation*}\Psi_{\mu}''(0)\leq(2+N)(2+N-\alpha\gamma_{\alpha})\mathcal{D}(a) \lt 0.\end{equation*}
\begin{equation*}\Psi_{\mu}''(0)\leq(2+N)(2+N-\alpha\gamma_{\alpha})\mathcal{D}(a) \lt 0.\end{equation*} Hence by Lemma 4.1 we have that ![]() $\mathcal{Q}_{\mu}(a)$ is a natural constraint of
$\mathcal{Q}_{\mu}(a)$ is a natural constraint of ![]() $I_{\mu}|_{S(a)}$.
$I_{\mu}|_{S(a)}$.
Lemma 4.4. For any ![]() $0 \lt \mu\leq1$ and any
$0 \lt \mu\leq1$ and any ![]() $u\in\mathcal{X}\setminus\{0\}$, if f(u) satisfies (F1) and (F2).
$u\in\mathcal{X}\setminus\{0\}$, if f(u) satisfies (F1) and (F2).
Then the following statements hold.
1) There exists a unique ![]() $s_{\mu}(u)\in\mathbb{R}$ such that
$s_{\mu}(u)\in\mathbb{R}$ such that ![]() $s_{\mu}(u)*u\in\mathcal{Q}_{\mu}(a)$, and
$s_{\mu}(u)*u\in\mathcal{Q}_{\mu}(a)$, and
 \begin{equation*}I_{\mu}(s_{\mu}(u)*u)=\max\limits_{s \gt 0}I_{\mu}(s*u).\end{equation*}
\begin{equation*}I_{\mu}(s_{\mu}(u)*u)=\max\limits_{s \gt 0}I_{\mu}(s*u).\end{equation*} 2) ![]() $I_{\mu}(s*u)$ is strictly increasing in
$I_{\mu}(s*u)$ is strictly increasing in ![]() $s\in(-\infty,s_{\mu}(u))$, is strictly decreasing in
$s\in(-\infty,s_{\mu}(u))$, is strictly decreasing in ![]() $s\in(s_{\mu}(u),+\infty)$,
$s\in(s_{\mu}(u),+\infty)$,
 \begin{equation*}\lim\limits_{s\rightarrow-\infty}I_{\mu}(s*u)=0^{+},\ \ \ \lim\limits_{s\rightarrow+\infty}I_{\mu}(s*u)=-\infty\ \ \ {\rm and}\ \ \ I_{\mu}(s_{\mu}(u)*u) \gt 0.\end{equation*}
\begin{equation*}\lim\limits_{s\rightarrow-\infty}I_{\mu}(s*u)=0^{+},\ \ \ \lim\limits_{s\rightarrow+\infty}I_{\mu}(s*u)=-\infty\ \ \ {\rm and}\ \ \ I_{\mu}(s_{\mu}(u)*u) \gt 0.\end{equation*} 3) ![]() $s_{\mu}(u) \lt 0$ if and only if
$s_{\mu}(u) \lt 0$ if and only if ![]() $Q_{\mu}(u) \lt 0$.
$Q_{\mu}(u) \lt 0$.
4) The map ![]() $u\in\mathcal{X}\setminus\{0\}\rightarrow s_{\mu}(u)\in\mathbb{R}$ is of class C 1.
$u\in\mathcal{X}\setminus\{0\}\rightarrow s_{\mu}(u)\in\mathbb{R}$ is of class C 1.
Proof. For any ![]() $0 \lt \mu\leq1$ and any
$0 \lt \mu\leq1$ and any ![]() $u\in S(a)$,
$u\in S(a)$, ![]() $|s*u|_{2}=a$ and
$|s*u|_{2}=a$ and ![]() $|\nabla (s*u)|_{2}=e^{s}|\nabla u|_{2}$. We deduce from (F1) that for all
$|\nabla (s*u)|_{2}=e^{s}|\nabla u|_{2}$. We deduce from (F1) that for all ![]() $t\in\mathbb{R}$,
$t\in\mathbb{R}$,
 \begin{equation*}\left\{\begin{aligned}
&s^{\beta}F(t)\leq F(ts) \leq s^{\alpha}F(t)\ \ \ {\rm if} \ s\leq1,\\
&s^{\alpha}F(t)\leq F(ts) \leq s^{\beta}F(t)\ \ \ {\rm if} \ s\geq1.
\end{aligned}
\right.\end{equation*}
\begin{equation*}\left\{\begin{aligned}
&s^{\beta}F(t)\leq F(ts) \leq s^{\alpha}F(t)\ \ \ {\rm if} \ s\leq1,\\
&s^{\alpha}F(t)\leq F(ts) \leq s^{\beta}F(t)\ \ \ {\rm if} \ s\geq1.
\end{aligned}
\right.\end{equation*}So for s < 0, we get:
 \begin{align*}
\Psi_{\mu}(s)=&I_{\mu}(s*u)\\
&=\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{-Ns}\int_{\mathbb{R}^{N}}F(e^{\frac{N}{2}s}u)\\
&\geq\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{-Ns}\cdot e^{\frac{N}{2}s\alpha}\int_{\mathbb{R}^{N}}F(u)\\
&=\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{\alpha\gamma_{\alpha}s}\int_{\mathbb{R}^{N}}F(u).
\end{align*}
\begin{align*}
\Psi_{\mu}(s)=&I_{\mu}(s*u)\\
&=\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{-Ns}\int_{\mathbb{R}^{N}}F(e^{\frac{N}{2}s}u)\\
&\geq\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{-Ns}\cdot e^{\frac{N}{2}s\alpha}\int_{\mathbb{R}^{N}}F(u)\\
&=\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{\alpha\gamma_{\alpha}s}\int_{\mathbb{R}^{N}}F(u).
\end{align*} Since ![]() $\alpha\gamma_{\alpha} \gt \theta+\theta\gamma_{\theta}$,
$\alpha\gamma_{\alpha} \gt \theta+\theta\gamma_{\theta}$, ![]() $\alpha\gamma_{\alpha} \gt 2$ and
$\alpha\gamma_{\alpha} \gt 2$ and ![]() $\alpha\gamma_{\alpha} \gt 2+N$ when
$\alpha\gamma_{\alpha} \gt 2+N$ when  $\alpha \gt 4+\frac{4}{N}$, then
$\alpha \gt 4+\frac{4}{N}$, then ![]() $\Psi_{\mu}(s)\rightarrow0^{+}$ as
$\Psi_{\mu}(s)\rightarrow0^{+}$ as ![]() $s\rightarrow-\infty$. For s > 1, we get:
$s\rightarrow-\infty$. For s > 1, we get:
 \begin{align*}
\Psi_{\mu}(s)=&I_{\mu}(s*u)\\
&\leq\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{\alpha\gamma_{\alpha}s}\int_{\mathbb{R}^{N}}F(u).
\end{align*}
\begin{align*}
\Psi_{\mu}(s)=&I_{\mu}(s*u)\\
&\leq\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\ & \qquad\qquad -e^{\alpha\gamma_{\alpha}s}\int_{\mathbb{R}^{N}}F(u).
\end{align*} In view of ![]() $\alpha\gamma_{\alpha} \gt \theta+\theta\gamma_{\theta}$,
$\alpha\gamma_{\alpha} \gt \theta+\theta\gamma_{\theta}$, ![]() $\alpha\gamma_{\alpha} \gt 2$ and
$\alpha\gamma_{\alpha} \gt 2$ and ![]() $\alpha\gamma_{\alpha} \gt 2+N$ when
$\alpha\gamma_{\alpha} \gt 2+N$ when  $\alpha \gt 4+\frac{4}{N}$, then
$\alpha \gt 4+\frac{4}{N}$, then ![]() $\Psi_{\mu}(s)\rightarrow-\infty$ as
$\Psi_{\mu}(s)\rightarrow-\infty$ as ![]() $s\rightarrow+\infty$. Therefore, there exists
$s\rightarrow+\infty$. Therefore, there exists ![]() $s_{1}\in\mathbb{R}$ such that:
$s_{1}\in\mathbb{R}$ such that:
 \begin{equation*}I_{\mu}(s_{1}*u)=\max\limits_{s \gt 0}I_{\mu}(s*u) \gt 0.\end{equation*}
\begin{equation*}I_{\mu}(s_{1}*u)=\max\limits_{s \gt 0}I_{\mu}(s*u) \gt 0.\end{equation*} Hence ![]() $\Psi_{\mu}'(s_{1})=0$ and by the Proposition 2.1, we get
$\Psi_{\mu}'(s_{1})=0$ and by the Proposition 2.1, we get ![]() $s_{1}*u\in\mathcal{Q}_{\mu}(a)$. Assume that there exists
$s_{1}*u\in\mathcal{Q}_{\mu}(a)$. Assume that there exists ![]() $s_{2}\in\mathbb{R}$ such that
$s_{2}\in\mathbb{R}$ such that ![]() $s_{2}*u\in\mathcal{Q}_{\mu}(a)$. Without loss of generality, suppose that
$s_{2}*u\in\mathcal{Q}_{\mu}(a)$. Without loss of generality, suppose that ![]() $s_{1} \lt s_{2}$, by Lemma 4.3, we have that s 1 and s 2 are strict local maximum of
$s_{1} \lt s_{2}$, by Lemma 4.3, we have that s 1 and s 2 are strict local maximum of ![]() $\Psi_{\mu}(s)$. Then there exists
$\Psi_{\mu}(s)$. Then there exists ![]() $s_{3}\in(s_{1},s_{2})$ such that:
$s_{3}\in(s_{1},s_{2})$ such that:
 \begin{equation*}\Psi_{\mu}(s_{3})=\min\limits_{s\in(s_{1},s_{2})}\Psi_{\mu}(s).\end{equation*}
\begin{equation*}\Psi_{\mu}(s_{3})=\min\limits_{s\in(s_{1},s_{2})}\Psi_{\mu}(s).\end{equation*} It follows that s 3 is a local minimum of ![]() $\Psi_{\mu}(s)$. So we get
$\Psi_{\mu}(s)$. So we get ![]() $\Psi_{\mu}'(s_{3})=0$ and
$\Psi_{\mu}'(s_{3})=0$ and ![]() $s_{3}*u\in\mathcal{Q}_{\mu}(a)$ with
$s_{3}*u\in\mathcal{Q}_{\mu}(a)$ with  $\Psi_{\mu,s_{3}*u}''(0)=I_{\mu}''(s_{3}*u)=\Psi_{\mu}''(s_{3})\geq0$, which is in contradiction with Lemma 4.3.
$\Psi_{\mu,s_{3}*u}''(0)=I_{\mu}''(s_{3}*u)=\Psi_{\mu}''(s_{3})\geq0$, which is in contradiction with Lemma 4.3.
By  $I_{\mu}(s_{\mu}(u)*u)=\max\limits_{s \gt 0}I_{\mu}(s*u) \gt 0$ and the uniqueness of
$I_{\mu}(s_{\mu}(u)*u)=\max\limits_{s \gt 0}I_{\mu}(s*u) \gt 0$ and the uniqueness of ![]() $s_{\mu}(u)$, we have that
$s_{\mu}(u)$, we have that ![]() $\Psi_{\mu}'(s) \gt 0$ in
$\Psi_{\mu}'(s) \gt 0$ in ![]() $s\in(-\infty,s_{\mu}(u))$ and
$s\in(-\infty,s_{\mu}(u))$ and ![]() $\Psi_{\mu}'(s) \lt 0$ in
$\Psi_{\mu}'(s) \lt 0$ in ![]() $s\in(s_{\mu}(u),+\infty)$. This implies that
$s\in(s_{\mu}(u),+\infty)$. This implies that ![]() $I_{\mu}(s*u)$ is strictly increasing in
$I_{\mu}(s*u)$ is strictly increasing in ![]() $s\in(-\infty,s_{\mu}(u))$ and is strictly decreasing in
$s\in(-\infty,s_{\mu}(u))$ and is strictly decreasing in ![]() $s\in(s_{\mu}(u),+\infty)$. So if
$s\in(s_{\mu}(u),+\infty)$. So if ![]() $s_{\mu}(u) \lt 0$ then
$s_{\mu}(u) \lt 0$ then ![]() $Q_{\mu}(u)=\Psi_{\mu}'(0) \lt 0$. On the other hand,
$Q_{\mu}(u)=\Psi_{\mu}'(0) \lt 0$. On the other hand, ![]() $Q_{\mu}(u)=\Psi_{\mu}'(0) \lt 0$, then
$Q_{\mu}(u)=\Psi_{\mu}'(0) \lt 0$, then ![]() $0\in(s_{\mu}(u),+\infty)$, so
$0\in(s_{\mu}(u),+\infty)$, so ![]() $s_{\mu}(u) \lt 0$.
$s_{\mu}(u) \lt 0$.
Now we prove that the map ![]() $u\in\mathcal{X}\setminus\{0\}\rightarrow s_{\mu}(u)\in\mathbb{R}$ is of class C 1. Let
$u\in\mathcal{X}\setminus\{0\}\rightarrow s_{\mu}(u)\in\mathbb{R}$ is of class C 1. Let ![]() $G_{\mu}(s):=\Psi_{\mu}'(s)$. Then
$G_{\mu}(s):=\Psi_{\mu}'(s)$. Then ![]() $G_{\mu}(s_{\mu}(u))=\Psi_{\mu}'(s_{\mu})=0$. Moreover, by Lemma 4.3 we have:
$G_{\mu}(s_{\mu}(u))=\Psi_{\mu}'(s_{\mu})=0$. Moreover, by Lemma 4.3 we have:
 \begin{equation*}G_{\mu}'(s_{\mu}(u))=\Psi_{\mu}''(s_{\mu}(u))=\Psi_{\mu,s_{\mu}(u)*u}''(0) \lt 0.\end{equation*}
\begin{equation*}G_{\mu}'(s_{\mu}(u))=\Psi_{\mu}''(s_{\mu}(u))=\Psi_{\mu,s_{\mu}(u)*u}''(0) \lt 0.\end{equation*} Then, the Implicit Function Theorem [Reference Chang11] implies that the map ![]() $u\in\mathcal{X}\setminus\{0\}\rightarrow s_{\mu}(u)\in\mathbb{R}$ is of class C 1.
$u\in\mathcal{X}\setminus\{0\}\rightarrow s_{\mu}(u)\in\mathbb{R}$ is of class C 1.
4.2. Ground state critical point of  $I_{\mu}|_{S(a)}$
$I_{\mu}|_{S(a)}$
In this subsection we study a minimization problem:
 \begin{equation*}m_{\mu}(a):=\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u).\end{equation*}
\begin{equation*}m_{\mu}(a):=\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u).\end{equation*} If ![]() $m_{\mu}(a)$ is achieved, we obtain a minimizer which is a ground state critical point of
$m_{\mu}(a)$ is achieved, we obtain a minimizer which is a ground state critical point of ![]() $I_{\mu}|_{S(a)}$.
$I_{\mu}|_{S(a)}$.
Lemma 4.5. For any ![]() $0 \lt \mu\leq1$, if f(u) satisfies (F1), we get:
$0 \lt \mu\leq1$, if f(u) satisfies (F1), we get:
 \begin{equation*}m_{\mu}(a)\geq\mathcal{D}_{0}(a):=\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\mathcal{D}(a) \gt 0.\end{equation*}
\begin{equation*}m_{\mu}(a)\geq\mathcal{D}_{0}(a):=\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\mathcal{D}(a) \gt 0.\end{equation*}Proof. Since ![]() $Q_{\mu}(u)=0$, then,
$Q_{\mu}(u)=0$, then,
 \begin{equation*}\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)]=0.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)]=0.
\end{aligned}
\end{equation*} We deduce from (F1) that ![]() $(\alpha-2)F(u)\leq f(u)u-2F(u)\leq(\beta-2)F(u)$, then
$(\alpha-2)F(u)\leq f(u)u-2F(u)\leq(\beta-2)F(u)$, then  $\widetilde{Q}_{\mu}(u)\geq 0$, where
$\widetilde{Q}_{\mu}(u)\geq 0$, where
 \begin{equation*}\widetilde{Q}_{\mu}(u)
=(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\alpha\gamma_{\alpha}\int_{\mathbb{R}^{N}}F(u).\end{equation*}
\begin{equation*}\widetilde{Q}_{\mu}(u)
=(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\alpha\gamma_{\alpha}\int_{\mathbb{R}^{N}}F(u).\end{equation*} Thus for any ![]() $u\in\mathcal{Q}_{\mu}(a)$, there is:
$u\in\mathcal{Q}_{\mu}(a)$, there is:
 \begin{equation*}\begin{aligned}I_{\mu}(u)
&\geq I_{\mu}(u)-\frac{1}{\alpha\gamma_{\alpha}}\widetilde{Q}_{\mu}(u)\\
&=\frac{\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta}}{\theta\alpha\gamma_{\alpha}}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\frac{\alpha\gamma_{\alpha}-2}{2\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}I_{\mu}(u)
&\geq I_{\mu}(u)-\frac{1}{\alpha\gamma_{\alpha}}\widetilde{Q}_{\mu}(u)\\
&=\frac{\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta}}{\theta\alpha\gamma_{\alpha}}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\frac{\alpha\gamma_{\alpha}-2}{2\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}.
\end{aligned}
\end{equation*} Since ![]() $\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta} \gt 0$,
$\alpha\gamma_{\alpha}-\theta-\theta\gamma_{\theta} \gt 0$, ![]() $\alpha\gamma_{\alpha}-2 \gt 0$ and
$\alpha\gamma_{\alpha}-2 \gt 0$ and ![]() $\alpha\gamma_{\alpha}-2-N \gt 0$, then
$\alpha\gamma_{\alpha}-2-N \gt 0$, then
 \begin{equation*}I_{\mu}(u)\geq\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
\geq\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\mathcal{D}(a) \gt 0.\end{equation*}
\begin{equation*}I_{\mu}(u)\geq\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
\geq\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\mathcal{D}(a) \gt 0.\end{equation*}Therefore
 \begin{equation*}m_{\mu}(a)\geq\mathcal{D}_{0}(a):=\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\mathcal{D}(a) \gt 0.\end{equation*}
\begin{equation*}m_{\mu}(a)\geq\mathcal{D}_{0}(a):=\frac{\alpha\gamma_{\alpha}-2-N}{\alpha\gamma_{\alpha}}\mathcal{D}(a) \gt 0.\end{equation*}Lemma 4.6. There exists a ρ > 0 which is small and is independent of µ such that for any ![]() $0 \lt \mu\leq1$, if f(u) satisfies (F1), then for any
$0 \lt \mu\leq1$, if f(u) satisfies (F1), then for any ![]() $u\in B_{\mu}(\rho,a)$, we get:
$u\in B_{\mu}(\rho,a)$, we get:
 \begin{equation*}0 \lt \sup\limits_{u\in B_{\mu}(\rho,a)}I_{\mu}(u) \lt \mathcal{D}_{0}(a) \ \ \ {\rm and} \ \ \ I_{\mu}(u),\ Q_{\mu}(u) \gt 0,\end{equation*}
\begin{equation*}0 \lt \sup\limits_{u\in B_{\mu}(\rho,a)}I_{\mu}(u) \lt \mathcal{D}_{0}(a) \ \ \ {\rm and} \ \ \ I_{\mu}(u),\ Q_{\mu}(u) \gt 0,\end{equation*}where
 \begin{equation*}B_{\mu}(\rho,a)=\left\{u\in S(a): \mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\leq\rho\right\}.\end{equation*}
\begin{equation*}B_{\mu}(\rho,a)=\left\{u\in S(a): \mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\leq\rho\right\}.\end{equation*}Proof. We get from the definition of ![]() $I_{\mu}(u)$ that:
$I_{\mu}(u)$ that:
 \begin{equation*}\sup\limits_{u\in B_{\mu}(\rho,a)}I_{\mu}(u)\leq\max\left\{\frac{1}{\theta},\frac{1}{2},1\right\}\rho \lt \mathcal{D}_{0}(a),\end{equation*}
\begin{equation*}\sup\limits_{u\in B_{\mu}(\rho,a)}I_{\mu}(u)\leq\max\left\{\frac{1}{\theta},\frac{1}{2},1\right\}\rho \lt \mathcal{D}_{0}(a),\end{equation*} where ρ > 0 is small and is not dependent of µ. For any ![]() $u\in\partial B_{\mu}(r,a)$ with
$u\in\partial B_{\mu}(r,a)$ with ![]() $0 \lt r \lt \rho$, by the inequality (1.6), we have,
$0 \lt r \lt \rho$, by the inequality (1.6), we have,
 \begin{equation*}\begin{aligned}\inf\limits_{u\in\partial B_{\mu}(r,a)}I_{\mu}(u)
\geq& \frac{\mu}{\theta}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-F(1)K_{1}(\alpha,N)a^{\frac{4N-\alpha(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\alpha-2)}{2(N+2)}}\\
&-F(1)K_{2}(\beta,N)a^{\frac{4N-\beta(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\beta-2)}{2(N+2)}}\\
\geq&\frac{\mu}{\theta}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+C\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
\geq& C_{1}(a,\theta,\alpha,\beta,N)r \gt 0.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}\inf\limits_{u\in\partial B_{\mu}(r,a)}I_{\mu}(u)
\geq& \frac{\mu}{\theta}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-F(1)K_{1}(\alpha,N)a^{\frac{4N-\alpha(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\alpha-2)}{2(N+2)}}\\
&-F(1)K_{2}(\beta,N)a^{\frac{4N-\beta(N-2)}{(N+2)}}
\left(\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\right)^{\frac{N(\beta-2)}{2(N+2)}}\\
\geq&\frac{\mu}{\theta}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+C\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
\geq& C_{1}(a,\theta,\alpha,\beta,N)r \gt 0.
\end{aligned}
\end{equation*}In the same way we also get:
 \begin{equation*}\inf\limits_{u\in\partial B_{\mu}(r,a)}Q_{\mu}(u)\geq C_{2}(a,\theta,\alpha,\beta,N)r \gt 0,\end{equation*}
\begin{equation*}\inf\limits_{u\in\partial B_{\mu}(r,a)}Q_{\mu}(u)\geq C_{2}(a,\theta,\alpha,\beta,N)r \gt 0,\end{equation*}we finish the proof.
To find a P.S. sequence, we study the augmented functional ![]() $\widetilde{I_{\mu}}$ which follows the strategy firstly introduced in [Reference Jeanjean18]
$\widetilde{I_{\mu}}$ which follows the strategy firstly introduced in [Reference Jeanjean18]
 \begin{align}
\widetilde{I_{\mu}}(s,u):=&I_{\mu}(s*u)\nonumber\\
=&\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta} + \frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\nonumber\\
& -e^{-Ns}\int_{\mathbb{R}^{N}}F(e^{\frac{N}{2}s}u),
\end{align}
\begin{align}
\widetilde{I_{\mu}}(s,u):=&I_{\mu}(s*u)\nonumber\\
=&\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta} + \frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\nonumber\\
& -e^{-Ns}\int_{\mathbb{R}^{N}}F(e^{\frac{N}{2}s}u),
\end{align} and look at the restriction  $\widetilde{I_{\mu}}|_{\mathbb{R}\times S(a)}$. We have that
$\widetilde{I_{\mu}}|_{\mathbb{R}\times S(a)}$. We have that ![]() $\widetilde{I_{\mu}}$ is of class C 1 and also a P.S. sequence for
$\widetilde{I_{\mu}}$ is of class C 1 and also a P.S. sequence for  $\widetilde{I_{\mu}}|_{\mathbb{R}\times S_{r}(a)}$ is a P.S. sequence for
$\widetilde{I_{\mu}}|_{\mathbb{R}\times S_{r}(a)}$ is a P.S. sequence for  $\widetilde{I_{\mu}}|_{\mathbb{R}\times S(a)}$ because
$\widetilde{I_{\mu}}|_{\mathbb{R}\times S(a)}$ because  $\widetilde{I_{\mu}}(u)$ is invariant under rotations.
$\widetilde{I_{\mu}}(u)$ is invariant under rotations.
Lemma 4.7. For ![]() $u\in S(a)$ and
$u\in S(a)$ and ![]() $s\in\mathbb{R}$, the map,
$s\in\mathbb{R}$, the map,
is a linear isomorphism with inverse ![]() $\psi\mapsto(-s)*\psi$, where
$\psi\mapsto(-s)*\psi$, where ![]() $T_{u}S(a)$ denotes the tangent space to S(a) in u.
$T_{u}S(a)$ denotes the tangent space to S(a) in u.
Proof. For any ![]() $u\in S(a)$ and
$u\in S(a)$ and ![]() $s\in\mathbb{R}$, by Lemma 3.6 in [Reference Barstch and Soave6], we can prove the map
$s\in\mathbb{R}$, by Lemma 3.6 in [Reference Barstch and Soave6], we can prove the map
is a linear isomorphism with inverse ![]() $\psi\mapsto(-s)*\psi$, here we omit it.
$\psi\mapsto(-s)*\psi$, here we omit it.
Denoting by ![]() $I_{\mu}^{c}$ the closed sublevel set
$I_{\mu}^{c}$ the closed sublevel set ![]() $\{u\in S(a): I_{\mu}(u)\leq c\}$, we introduce the minimax class:
$\{u\in S(a): I_{\mu}(u)\leq c\}$, we introduce the minimax class:
 \begin{equation*}\Gamma:=\{\gamma(\tau)=(\alpha,\beta)\in C([0,1],\mathbb{R}\times S_{r}(a));
\ \gamma(0)\in (0,B_{\mu}(\rho,a)),\ \gamma(1)\in (0,I_{\mu}^{0})\},\end{equation*}
\begin{equation*}\Gamma:=\{\gamma(\tau)=(\alpha,\beta)\in C([0,1],\mathbb{R}\times S_{r}(a));
\ \gamma(0)\in (0,B_{\mu}(\rho,a)),\ \gamma(1)\in (0,I_{\mu}^{0})\},\end{equation*}with the minimax level:
 \begin{equation*}\sigma_{\mu}(a):=\inf\limits_{\gamma\in \Gamma}\max\limits_{(s,u)\in \gamma([0,1])}\widetilde{I}_{\mu}(s,u).\end{equation*}
\begin{equation*}\sigma_{\mu}(a):=\inf\limits_{\gamma\in \Gamma}\max\limits_{(s,u)\in \gamma([0,1])}\widetilde{I}_{\mu}(s,u).\end{equation*}Lemma 4.8. For any ![]() $0 \lt \mu\leq1$,
$0 \lt \mu\leq1$, ![]() $m_{\mu}(a)=\sigma_{\mu}(a)$.
$m_{\mu}(a)=\sigma_{\mu}(a)$.
Proof. For any ![]() $0 \lt \mu\leq1$ and any
$0 \lt \mu\leq1$ and any ![]() $u\in S_{r}(a)$. Since
$u\in S_{r}(a)$. Since ![]() $I_{\mu}(s*u)\rightarrow0^{+}$, then there exists
$I_{\mu}(s*u)\rightarrow0^{+}$, then there exists ![]() $s_{0} \lt \lt -1$, such that
$s_{0} \lt \lt -1$, such that ![]() $s_{0}*u\in B_{\mu}(\rho,a)$,
$s_{0}*u\in B_{\mu}(\rho,a)$, ![]() $I_{\mu}(s_{0}*u) \gt 0$ and
$I_{\mu}(s_{0}*u) \gt 0$ and ![]() $Q_{\mu}(s_{0}*u) \gt 0$. By Lemma 4.4 there exists
$Q_{\mu}(s_{0}*u) \gt 0$. By Lemma 4.4 there exists ![]() $s_{1} \gt \gt 1$ such that
$s_{1} \gt \gt 1$ such that ![]() $I_{\mu}(s_{1}*u) \lt 0$. We deduce from the continuity of
$I_{\mu}(s_{1}*u) \lt 0$. We deduce from the continuity of ![]() $s\in \mathbb{R}\mapsto s*u\in S_{r}(a)$ that:
$s\in \mathbb{R}\mapsto s*u\in S_{r}(a)$ that:
is a path in Γ. Hence the minimax value ![]() $\sigma_{\mu}(a)$ is a real number.
$\sigma_{\mu}(a)$ is a real number.
We claim that ![]() $\forall \gamma\in \Gamma$, there exists
$\forall \gamma\in \Gamma$, there exists ![]() $\chi_{\gamma}\in (0,1)$ such that
$\chi_{\gamma}\in (0,1)$ such that ![]() $\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}(a)$. Indeed, since
$\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}(a)$. Indeed, since ![]() $\gamma(0)=(\alpha(0),\beta(0))\in (0,B_{\mu}(\rho,a))$, we have:
$\gamma(0)=(\alpha(0),\beta(0))\in (0,B_{\mu}(\rho,a))$, we have:
Also since  $I_{\mu}(\beta(1))=\widetilde{I}_{\mu}(\alpha(1),\beta(1))=\widetilde{I}_{\mu}(\gamma(1)) \lt 0$, we deduce from Proposition 2.1 and Lemma 4.4 that
$I_{\mu}(\beta(1))=\widetilde{I}_{\mu}(\alpha(1),\beta(1))=\widetilde{I}_{\mu}(\gamma(1)) \lt 0$, we deduce from Proposition 2.1 and Lemma 4.4 that ![]() $s_{\mu}(\beta(1)) \lt 0$, which implies that
$s_{\mu}(\beta(1)) \lt 0$, which implies that ![]() $Q_{\mu}(\beta(1)) \lt 0$. Moreover, the map
$Q_{\mu}(\beta(1)) \lt 0$. Moreover, the map ![]() $Q_{\mu}(\alpha(\chi)*\beta(\chi))$ is continuous in Γ. It follows that for any
$Q_{\mu}(\alpha(\chi)*\beta(\chi))$ is continuous in Γ. It follows that for any ![]() $\gamma\in \Gamma$, there exists
$\gamma\in \Gamma$, there exists ![]() $\chi_{\gamma}\in (0,1)$ such that
$\chi_{\gamma}\in (0,1)$ such that ![]() $Q_{\mu}(\alpha(\chi_{\gamma})*\beta(\chi_{\gamma}))=0$, in the sense that
$Q_{\mu}(\alpha(\chi_{\gamma})*\beta(\chi_{\gamma}))=0$, in the sense that ![]() $\alpha(\tau_{\gamma})*\beta(\tau_{\gamma})\in \mathcal{Q}_{\mu}(a)$.
$\alpha(\tau_{\gamma})*\beta(\tau_{\gamma})\in \mathcal{Q}_{\mu}(a)$.
For any ![]() $\gamma\in \Gamma$, we get from
$\gamma\in \Gamma$, we get from ![]() $\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}(a)$ that:
$\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}(a)$ that:
 \begin{equation*}\max\limits_{\gamma([0,1])}\widetilde{I}_{\mu}\geq\widetilde{I}_{\mu}(\gamma(\chi_{\gamma}))=I_{\mu}(\alpha(\chi_{\gamma})*\beta(\chi_{\gamma}))\geq \inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu},\end{equation*}
\begin{equation*}\max\limits_{\gamma([0,1])}\widetilde{I}_{\mu}\geq\widetilde{I}_{\mu}(\gamma(\chi_{\gamma}))=I_{\mu}(\alpha(\chi_{\gamma})*\beta(\chi_{\gamma}))\geq \inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu},\end{equation*} which deduces that  $\sigma_{\mu}(a)\geq \inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}$. On the other hand, if
$\sigma_{\mu}(a)\geq \inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}$. On the other hand, if ![]() $u\in \mathcal{Q}_{\mu}(a)\cap S_{r}(a)$, then γu defined in (4.3) is a path in Γ with:
$u\in \mathcal{Q}_{\mu}(a)\cap S_{r}(a)$, then γu defined in (4.3) is a path in Γ with:
 \begin{equation*}I_{\mu}(u)=\widetilde{I}_{\mu}(0,u)=\max\limits_{\gamma_{u}([0,1])}\widetilde{I}_{\mu}\geq \sigma_{\mu}(a),\end{equation*}
\begin{equation*}I_{\mu}(u)=\widetilde{I}_{\mu}(0,u)=\max\limits_{\gamma_{u}([0,1])}\widetilde{I}_{\mu}\geq \sigma_{\mu}(a),\end{equation*} which gives  $\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}\geq \sigma_{\mu}(a)$, thus
$\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}\geq \sigma_{\mu}(a)$, thus  $\sigma_{\mu}(a)=\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}.$ In order to prove the equality
$\sigma_{\mu}(a)=\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}.$ In order to prove the equality  $m_{\mu}(a)=\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}$, we only need to prove that:
$m_{\mu}(a)=\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}$, we only need to prove that:
 \begin{equation*}m_{\mu}(a)\geq\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}.\end{equation*}
\begin{equation*}m_{\mu}(a)\geq\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu}.\end{equation*}By the symmetric decreasing rearrangement [Reference Lieb and Loss22], we see that the above inequality can be achieved easily.
Existence of the ground state for ![]() $I_{\mu}|_{S(a)}$.
$I_{\mu}|_{S(a)}$.
When N = 1, we take µ = 0 and the process is similar to the case of ![]() $N\geq2$, so we focus on the case
$N\geq2$, so we focus on the case ![]() $N\geq2$. Firstly, for any
$N\geq2$. Firstly, for any ![]() $0 \lt \mu\leq1$, Lemma 4.4, Lemma 4.5 and Lemma 4.8 imply that:
$0 \lt \mu\leq1$, Lemma 4.4, Lemma 4.5 and Lemma 4.8 imply that:
 \begin{equation*}m_{\mu}(a)=\sigma_{\mu}(a)=\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu} \gt 0\geq
\sup\limits_{(\mathcal{Q}_{\mu}(a)\cup I_{\mu}^{0})\cap S_{r}(a)}I_{\mu}
=\sup\limits_{((0,\mathcal{Q}_{\mu}(a))\cup (0,I_{\mu}^{0}))\cap S_{r}(a)}I_{\mu}.\end{equation*}
\begin{equation*}m_{\mu}(a)=\sigma_{\mu}(a)=\inf\limits_{\mathcal{Q}_{\mu}(a)\cap S_{r}(a)}I_{\mu} \gt 0\geq
\sup\limits_{(\mathcal{Q}_{\mu}(a)\cup I_{\mu}^{0})\cap S_{r}(a)}I_{\mu}
=\sup\limits_{((0,\mathcal{Q}_{\mu}(a))\cup (0,I_{\mu}^{0}))\cap S_{r}(a)}I_{\mu}.\end{equation*} By using the terminology in Section 5 [Reference Ghoussoub17], we get that ![]() $\{\gamma([0,1]):\gamma\in\Gamma\}$ is a homotopic stable family with extended closed boundary
$\{\gamma([0,1]):\gamma\in\Gamma\}$ is a homotopic stable family with extended closed boundary  $(0,B_{\mu}(\rho,a))\cup(0,I_{\mu}^{0})$, where
$(0,B_{\mu}(\rho,a))\cup(0,I_{\mu}^{0})$, where ![]() $\gamma([0,1])$ is the compact subset of
$\gamma([0,1])$ is the compact subset of ![]() $\mathbb{R}\times S_{r}(a)$. We also deduce that the superlevel set
$\mathbb{R}\times S_{r}(a)$. We also deduce that the superlevel set  $\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a)\}$ is a dual set, in the sense that
$\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a)\}$ is a dual set, in the sense that  $\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a)\}$ satisfies the assumptions (F’1) and (F’2) in Theorem 5.2 [Reference Ghoussoub17]. Hence we can take any minimizing sequence
$\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a)\}$ satisfies the assumptions (F’1) and (F’2) in Theorem 5.2 [Reference Ghoussoub17]. Hence we can take any minimizing sequence ![]() $\{\gamma_{n}=(\alpha_{n},\beta_{n})\}\subset\Gamma$ for
$\{\gamma_{n}=(\alpha_{n},\beta_{n})\}\subset\Gamma$ for ![]() $\sigma_{\mu}(a),$ with the property that
$\sigma_{\mu}(a),$ with the property that ![]() $\alpha_{n}\equiv0$ and
$\alpha_{n}\equiv0$ and ![]() $\beta_{n}\geq0$ a.e. on
$\beta_{n}\geq0$ a.e. on ![]() $\mathbb{R}^{N}$ for every
$\mathbb{R}^{N}$ for every ![]() $\chi\in[0,1]$, there exists a P.S. sequence
$\chi\in[0,1]$, there exists a P.S. sequence ![]() $\{(s_{n},w_{n})\}\subset\mathbb{R}\times S_{r}(a)$ for
$\{(s_{n},w_{n})\}\subset\mathbb{R}\times S_{r}(a)$ for  $\widetilde{I}_{\mu}|_{\mathbb{R}\times S_{r}(a)}$ at level
$\widetilde{I}_{\mu}|_{\mathbb{R}\times S_{r}(a)}$ at level ![]() $\sigma_{\mu}(a)$, that is:
$\sigma_{\mu}(a)$, that is:
 \begin{equation}
\partial_{s}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0 \ \ \ {\rm and}\ \ \ \partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,
\end{equation}
\begin{equation}
\partial_{s}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0 \ \ \ {\rm and}\ \ \ \partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,
\end{equation}with the additional property that:
By (4.2) and (4.4), we have ![]() $Q_{\mu}(s_{n}*w_{n})\rightarrow0$ and
$Q_{\mu}(s_{n}*w_{n})\rightarrow0$ and
 \begin{equation*}\|\partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\|_{(T_{w_{n}}S_{r}(a))^{*}}\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,\end{equation*}
\begin{equation*}\|\partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\|_{(T_{w_{n}}S_{r}(a))^{*}}\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,\end{equation*} Since ![]() $\{s_{n}\}$ is bounded due to (4.5), this implies that:
$\{s_{n}\}$ is bounded due to (4.5), this implies that:
Let then ![]() $u_{n}:=s_{n}*w_{n}$. By Lemma 4.7 equation (4.6) establishes that
$u_{n}:=s_{n}*w_{n}$. By Lemma 4.7 equation (4.6) establishes that ![]() $\{u_{n}\}\subset S_{r}(a)$ is a P.S. sequence for
$\{u_{n}\}\subset S_{r}(a)$ is a P.S. sequence for ![]() $I_{\mu}|_{S_{r}(a)},$ at level
$I_{\mu}|_{S_{r}(a)},$ at level ![]() $\sigma_{\mu}(a) \gt 0$ with
$\sigma_{\mu}(a) \gt 0$ with ![]() $Q_{\mu}(u_{n})\rightarrow0$. Thus it is also a P.S. sequence for
$Q_{\mu}(u_{n})\rightarrow0$. Thus it is also a P.S. sequence for ![]() $I_{\mu}|_{S(a)}$ at level
$I_{\mu}|_{S(a)}$ at level ![]() $\sigma_{\mu}(a) \gt 0$ with
$\sigma_{\mu}(a) \gt 0$ with ![]() $Q_{\mu}(u_{n})\rightarrow0$ because the problem is invariant under rotations. We deduce from Lemma 3.1 that up to a subsequence such that
$Q_{\mu}(u_{n})\rightarrow0$ because the problem is invariant under rotations. We deduce from Lemma 3.1 that up to a subsequence such that ![]() $u_{n}\rightarrow u_{\mu}$ in
$u_{n}\rightarrow u_{\mu}$ in ![]() $\mathcal{X}$, where
$\mathcal{X}$, where ![]() $u_{\mu}\in S(a)$ is a radially symmetric and real function. From (4.5) we have that
$u_{\mu}\in S(a)$ is a radially symmetric and real function. From (4.5) we have that ![]() $u_{\mu}\geq0$ a.e. on
$u_{\mu}\geq0$ a.e. on ![]() $\mathbb{R}^{N}$, finally the strong maximum principle shows that
$\mathbb{R}^{N}$, finally the strong maximum principle shows that ![]() $u_{\mu} \gt 0$.
$u_{\mu} \gt 0$.
5. The critical points of perturbed functional for Theorem 1.1
5.1. Properties of  $\mathcal{Q}_{\mu}(a)$
$\mathcal{Q}_{\mu}(a)$
Lemma 5.1. Let ![]() $0 \lt \mu\leq1$, under the assumption of (1.10), then
$0 \lt \mu\leq1$, under the assumption of (1.10), then  $\mathcal{Q}_{\mu}^{0}(a)=\emptyset$.
$\mathcal{Q}_{\mu}^{0}(a)=\emptyset$.
Proof. Suppose that there exists  $u\in \mathcal{Q}_{\mu}^{0}(a)$, then we get
$u\in \mathcal{Q}_{\mu}^{0}(a)$, then we get ![]() $Q_{\mu}(u)=0$ and
$Q_{\mu}(u)=0$ and ![]() $\Psi_{\mu}''(u)=0$,
$\Psi_{\mu}''(u)=0$,
 \begin{equation}
\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau\gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q}
-\gamma_{p}\int_{\mathbb{R}^{N}}|u|^{p}=0,
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}&(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\int_{\mathbb{R}^{N}}|\nabla u|^{2}
+(2+N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau\gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q}
-\gamma_{p}\int_{\mathbb{R}^{N}}|u|^{p}=0,
\end{aligned}
\end{equation} \begin{equation}
\begin{aligned}&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau q\gamma_{q}^{2}\int_{\mathbb{R}^{N}}|u|^{q}-p\gamma_{p}^{2}\int_{\mathbb{R}^{N}}|u|^{p}=0.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau q\gamma_{q}^{2}\int_{\mathbb{R}^{N}}|u|^{q}-p\gamma_{p}^{2}\int_{\mathbb{R}^{N}}|u|^{p}=0.
\end{aligned}
\end{equation}Combining (5.1) with (5.2), we have:
 \begin{equation*}\begin{aligned}&(1+\gamma_{\theta})(p\gamma_{p}-\theta-\theta\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+(p\gamma_{p}-2)\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
&+(2+N)(p\gamma_{p}-2-N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})\int_{\mathbb{R}^{N}}|u|^{q}=0,\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}&(1+\gamma_{\theta})(p\gamma_{p}-\theta-\theta\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+(p\gamma_{p}-2)\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
&+(2+N)(p\gamma_{p}-2-N)\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})\int_{\mathbb{R}^{N}}|u|^{q}=0,\end{aligned}
\end{equation*} Since ![]() $p\gamma_{p} \gt \theta+\theta\gamma_{\theta}$,
$p\gamma_{p} \gt \theta+\theta\gamma_{\theta}$, ![]() $p\gamma_{p} \gt 2$,
$p\gamma_{p} \gt 2$, ![]() $p\gamma_{p} \gt 2+N$ and
$p\gamma_{p} \gt 2+N$ and ![]() $p\gamma_{p} \gt q\gamma_{q}$ when
$p\gamma_{p} \gt q\gamma_{q}$ when  $p \gt 4+\frac{4}{N}$, then we get:
$p \gt 4+\frac{4}{N}$, then we get:
 \begin{equation*}(p\gamma_{p}-2)|\nabla u|_{2}^{2}\leq\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})|u|_{q}^{q}.\end{equation*}
\begin{equation*}(p\gamma_{p}-2)|\nabla u|_{2}^{2}\leq\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})|u|_{q}^{q}.\end{equation*}We deduce from the Gagliardo–Nirenberg inequality that:
 \begin{equation}
\begin{aligned}|\nabla u|_{2}^{2}&\leq\frac{\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})}{p\gamma_{p}-2}|u|_{q}^{q}\\
&\leq\frac{\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})}{p\gamma_{p}-2}C_{N,q}^{q}|\nabla u|_{2}^{q\gamma_{q}}a^{(1-\gamma_{q})q}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}|\nabla u|_{2}^{2}&\leq\frac{\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})}{p\gamma_{p}-2}|u|_{q}^{q}\\
&\leq\frac{\tau\gamma_{q}(p\gamma_{p}-q\gamma_{q})}{p\gamma_{p}-2}C_{N,q}^{q}|\nabla u|_{2}^{q\gamma_{q}}a^{(1-\gamma_{q})q}.
\end{aligned}
\end{equation}In the same way we get,
 \begin{equation}
|\nabla u|_{2}^{2}\leq\frac{\gamma_{p}(p\gamma_{p}-q\gamma_{q})}{2-q\gamma_{q}}C_{N,p}^{p}|\nabla u|_{2}^{p\gamma_{p}}a^{(1-\gamma_{p})p}.
\end{equation}
\begin{equation}
|\nabla u|_{2}^{2}\leq\frac{\gamma_{p}(p\gamma_{p}-q\gamma_{q})}{2-q\gamma_{q}}C_{N,p}^{p}|\nabla u|_{2}^{p\gamma_{p}}a^{(1-\gamma_{p})p}.
\end{equation}From (5.3) and (5.4) we conclude that:
 \begin{equation*}\left(C_{N,p}^{p}\gamma_{p}\frac{p\gamma_{p}-q\gamma_{q}}{2-q\gamma_{q}}\right)^{\frac{1}{2-p\gamma_{p}}}
a^{-\frac{(1-\gamma_{p})p}{p\gamma_{p}-2}}
\leq\left(C_{N,q}^{q}\gamma_{q}\frac {p\gamma_{p}-q\gamma_{q}}{p\gamma_{p}-2}\right)^{\frac{1}{2-q\gamma_{q}}}
\left(\tau a^{(1-\gamma_{q})q}\right)^{\frac{1}{2-q\gamma_{q}}},\end{equation*}
\begin{equation*}\left(C_{N,p}^{p}\gamma_{p}\frac{p\gamma_{p}-q\gamma_{q}}{2-q\gamma_{q}}\right)^{\frac{1}{2-p\gamma_{p}}}
a^{-\frac{(1-\gamma_{p})p}{p\gamma_{p}-2}}
\leq\left(C_{N,q}^{q}\gamma_{q}\frac {p\gamma_{p}-q\gamma_{q}}{p\gamma_{p}-2}\right)^{\frac{1}{2-q\gamma_{q}}}
\left(\tau a^{(1-\gamma_{q})q}\right)^{\frac{1}{2-q\gamma_{q}}},\end{equation*}that is
 \begin{align}
& \left(\frac{2-q\gamma_{q}}{C_{N,p}^{p}\gamma_{p}(p\gamma_{p}-q\gamma_{q})}\right)^{2-q\gamma_{q}}
\left(\frac{p\gamma_{p}-2}{C_{N,q}^{q}\gamma_{q}(p\gamma_{p}-q\gamma_{q})}\right)^{p\gamma_{p}}\nonumber
\\& \qquad\qquad \leq\left(\tau a^{(1-\gamma_{q})q}\right)^{p\gamma_{p}-2}\left(a^{(1-\gamma_{p})p}\right)^{2-q\gamma_{q}}.
\end{align}
\begin{align}
& \left(\frac{2-q\gamma_{q}}{C_{N,p}^{p}\gamma_{p}(p\gamma_{p}-q\gamma_{q})}\right)^{2-q\gamma_{q}}
\left(\frac{p\gamma_{p}-2}{C_{N,q}^{q}\gamma_{q}(p\gamma_{p}-q\gamma_{q})}\right)^{p\gamma_{p}}\nonumber
\\& \qquad\qquad \leq\left(\tau a^{(1-\gamma_{q})q}\right)^{p\gamma_{p}-2}\left(a^{(1-\gamma_{p})p}\right)^{2-q\gamma_{q}}.
\end{align} It is easy to check that this is in contradiction with (1.10), this implies that  $\mathcal{Q}_{\mu}^{0}(a)=\emptyset$.
$\mathcal{Q}_{\mu}^{0}(a)=\emptyset$.
Lemma 5.2. Let ![]() $0 \lt \mu\leq1$, under the assumption of (1.10), then
$0 \lt \mu\leq1$, under the assumption of (1.10), then ![]() $\mathcal{Q}_{\mu}(a)$ is a C 1-submanifold of codimension 1 in S(a).
$\mathcal{Q}_{\mu}(a)$ is a C 1-submanifold of codimension 1 in S(a).
Proof. ![]() $\mathcal{Q}_{\mu}(a)$ is a subset of
$\mathcal{Q}_{\mu}(a)$ is a subset of ![]() $\mathcal{X}$ and defined by
$\mathcal{X}$ and defined by ![]() $G(u)=0$ and
$G(u)=0$ and ![]() $Q_{\mu}(u)=0$, where
$Q_{\mu}(u)=0$, where
 \begin{equation*}G(u)=a^{2}-\int_{\mathbb{R}^{N}}|u|^{2},\end{equation*}
\begin{equation*}G(u)=a^{2}-\int_{\mathbb{R}^{N}}|u|^{2},\end{equation*} clearly ![]() $G\in C^{1}(\mathcal{X})$. Then we only need to check that
$G\in C^{1}(\mathcal{X})$. Then we only need to check that
If ![]() $dQ_{\mu}$ and dG(u) are linearly dependent, in the sense that there exists
$dQ_{\mu}$ and dG(u) are linearly dependent, in the sense that there exists ![]() $\nu\in\mathbb{R}$ such that:
$\nu\in\mathbb{R}$ such that:
 \begin{align*}
2\nu\int_{\mathbb{R}^{N}}u\phi=
& \theta(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta-2}\nabla u\nabla \phi
+2\int_{\mathbb{R}^{N}}\nabla u\nabla \phi+(2+N)2\nonumber \\ & \quad \int_{\mathbb{R}^{N}}(|u|^{2}\nabla u\nabla \phi+u\phi|\nabla u|^{2}) -\tau q\gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q-2}u\phi-p\gamma_{p}\int_{\mathbb{R}^{N}}|u|^{p-2}u\phi,
\end{align*}
\begin{align*}
2\nu\int_{\mathbb{R}^{N}}u\phi=
& \theta(1+\gamma_{\theta})\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta-2}\nabla u\nabla \phi
+2\int_{\mathbb{R}^{N}}\nabla u\nabla \phi+(2+N)2\nonumber \\ & \quad \int_{\mathbb{R}^{N}}(|u|^{2}\nabla u\nabla \phi+u\phi|\nabla u|^{2}) -\tau q\gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q-2}u\phi-p\gamma_{p}\int_{\mathbb{R}^{N}}|u|^{p-2}u\phi,
\end{align*} for any ![]() $\phi\in\mathcal{X}$. Testing the above equality with
$\phi\in\mathcal{X}$. Testing the above equality with ![]() $\phi=x\cdot\nabla u$ and
$\phi=x\cdot\nabla u$ and ![]() $\phi=u$, we get:
$\phi=u$, we get:
 \begin{equation*}\begin{aligned}0=&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau q\gamma_{q}^{2}\int_{\mathbb{R}^{N}}|u|^{q}-p\gamma_{p}^{2}\int_{\mathbb{R}^{N}}|u|^{p},
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}0=&\theta(1+\gamma_{\theta})^{2}\mu\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}
+2\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)^{2}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau q\gamma_{q}^{2}\int_{\mathbb{R}^{N}}|u|^{q}-p\gamma_{p}^{2}\int_{\mathbb{R}^{N}}|u|^{p},
\end{aligned}
\end{equation*} it shows that  $u\in \mathcal{Q}_{\mu}^{0}(a)$, which is contradicts with
$u\in \mathcal{Q}_{\mu}^{0}(a)$, which is contradicts with  $\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, hence
$\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, hence
which finish the proof.
For any ![]() $0 \lt \mu\leq1$ and any
$0 \lt \mu\leq1$ and any ![]() $u\in S(a)$, we have,
$u\in S(a)$, we have,
 \begin{equation}
\begin{aligned}I_{\mu}(u)&\geq E(u)
=\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}-\frac{\tau}{q}\int_{\mathbb{R}^{N}}|u|^{q}-\frac{1}{p}\int_{\mathbb{R}^{N}}|u|^{p}\\
&\geq\frac{1}{2}|\nabla u|_{2}^{2}-\frac{\tau C_{N,q}^{q}}{q}a^{(1-\gamma_{q})q}|\nabla u|_{2}^{q\gamma_{q}}-\frac{C_{N,p}^{p}}{p}a^{(1-\gamma_{p})p}|\nabla u|_{2}^{p\gamma_{p}}.\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}I_{\mu}(u)&\geq E(u)
=\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}-\frac{\tau}{q}\int_{\mathbb{R}^{N}}|u|^{q}-\frac{1}{p}\int_{\mathbb{R}^{N}}|u|^{p}\\
&\geq\frac{1}{2}|\nabla u|_{2}^{2}-\frac{\tau C_{N,q}^{q}}{q}a^{(1-\gamma_{q})q}|\nabla u|_{2}^{q\gamma_{q}}-\frac{C_{N,p}^{p}}{p}a^{(1-\gamma_{p})p}|\nabla u|_{2}^{p\gamma_{p}}.\end{aligned}
\end{equation} Hence it is natural to study the function ![]() $h:\mathbb{R}^{+}\rightarrow\mathbb{R}$:
$h:\mathbb{R}^{+}\rightarrow\mathbb{R}$:
 \begin{equation*}h(t):=\frac{1}{2}t^{2}-\frac{\tau C_{N,q}^{q}}{q}a^{(1-\gamma_{q})q}t^{q\gamma_{q}}-\frac{C_{N,p}^{p}}{p}a^{(1-\gamma_{p})p}t^{p\gamma_{p}},\end{equation*}
\begin{equation*}h(t):=\frac{1}{2}t^{2}-\frac{\tau C_{N,q}^{q}}{q}a^{(1-\gamma_{q})q}t^{q\gamma_{q}}-\frac{C_{N,p}^{p}}{p}a^{(1-\gamma_{p})p}t^{p\gamma_{p}},\end{equation*} to understand the geometry of the functional ![]() $I_{\mu}|_{S(a)}$. Since τ > 0 and
$I_{\mu}|_{S(a)}$. Since τ > 0 and ![]() $q\gamma_{q} \lt 2 \lt p\gamma_{p}$, we see that
$q\gamma_{q} \lt 2 \lt p\gamma_{p}$, we see that ![]() $h(0^{+})=0^{-}$ and
$h(0^{+})=0^{-}$ and ![]() $h(+\infty)=-\infty$. Under the assumption (1.10), we deduce from Lemma 5.1 [Reference Soave36] that the function h has two extreme points, one is a local strict minimum at negative level, the other one is a global strict maximum at positive level. Moreover, there exist
$h(+\infty)=-\infty$. Under the assumption (1.10), we deduce from Lemma 5.1 [Reference Soave36] that the function h has two extreme points, one is a local strict minimum at negative level, the other one is a global strict maximum at positive level. Moreover, there exist ![]() $0 \lt R_{0} \lt R_{1}$, both depending on a and τ, such that
$0 \lt R_{0} \lt R_{1}$, both depending on a and τ, such that ![]() $h(R_{0})=0=h(R_{1})$ and
$h(R_{0})=0=h(R_{1})$ and ![]() $h(t) \gt 0$ if and only if
$h(t) \gt 0$ if and only if ![]() $t\in (R_{0},R_{1})$.
$t\in (R_{0},R_{1})$.
Lemma 5.3. For any ![]() $0 \lt \mu\leq1$ and any
$0 \lt \mu\leq1$ and any ![]() $u\in S(a)$, under the assumption of (1.10), the function
$u\in S(a)$, under the assumption of (1.10), the function ![]() $\Psi_{\mu}$ has exactly two critical points
$\Psi_{\mu}$ has exactly two critical points ![]() $s_{\mu}(u) \lt t_{\mu}(u)\in\mathbb{R}$ and two zeros
$s_{\mu}(u) \lt t_{\mu}(u)\in\mathbb{R}$ and two zeros ![]() $c_{\mu}(u) \lt d_{\mu}(u)\in\mathbb{R}$, with
$c_{\mu}(u) \lt d_{\mu}(u)\in\mathbb{R}$, with ![]() $s_{\mu}(u) \lt c_{\mu}(u) \lt t_{\mu}(u) \lt d_{\mu}(u)$. Moreover:
$s_{\mu}(u) \lt c_{\mu}(u) \lt t_{\mu}(u) \lt d_{\mu}(u)$. Moreover:
1) ![]() $s_{\mu}(u)*u\in\mathcal{Q}_{\mu}^{+}(a)$,
$s_{\mu}(u)*u\in\mathcal{Q}_{\mu}^{+}(a)$, ![]() $t_{\mu}(u)*u\in\mathcal{Q}_{\mu}^{-}(a)$, and
$t_{\mu}(u)*u\in\mathcal{Q}_{\mu}^{-}(a)$, and ![]() $s*u\in\mathcal{Q}_{\mu}(a)$ if and only if
$s*u\in\mathcal{Q}_{\mu}(a)$ if and only if ![]() $s=s_{\mu}(u)$ or
$s=s_{\mu}(u)$ or ![]() $s=t_{\mu}(u)$.
$s=t_{\mu}(u)$.
2) ![]() $|\nabla (s*u)|_{2}\leq R_{0}$ for any
$|\nabla (s*u)|_{2}\leq R_{0}$ for any ![]() $s\leq c_{\mu}(u)$, and
$s\leq c_{\mu}(u)$, and
3) We get
and ![]() $\Psi_{\mu}$ is strictly decreasing and concave on
$\Psi_{\mu}$ is strictly decreasing and concave on ![]() $(t_{\mu}(u),+\infty)$. In particular,
$(t_{\mu}(u),+\infty)$. In particular, ![]() $t_{\mu}(u) \lt 0$ if and only if
$t_{\mu}(u) \lt 0$ if and only if ![]() $Q_{\mu}(u) \lt 0$.
$Q_{\mu}(u) \lt 0$.
4) The maps ![]() $u\in S(a)\mapsto s_{\mu}(u)\in\mathbb{R}$ and
$u\in S(a)\mapsto s_{\mu}(u)\in\mathbb{R}$ and ![]() $u\in S(a)\mapsto t_{\mu}(u)\in\mathbb{R}$ are of class C 1.
$u\in S(a)\mapsto t_{\mu}(u)\in\mathbb{R}$ are of class C 1.
Proof. Let ![]() $0 \lt \mu\leq1$ and
$0 \lt \mu\leq1$ and ![]() $u\in S(a)$. By Proposition 2.1 we know that
$u\in S(a)$. By Proposition 2.1 we know that ![]() $s*u\in Q_{\mu}(a)$ if and only if
$s*u\in Q_{\mu}(a)$ if and only if ![]() $\Psi_{\mu}'(s)=0$. Thus we prove that
$\Psi_{\mu}'(s)=0$. Thus we prove that ![]() $\Psi_{\mu}$ has at least two critical points at first. Recalling (4.6), we get:
$\Psi_{\mu}$ has at least two critical points at first. Recalling (4.6), we get:
Hence the C 2 function ![]() $\Psi_{\mu}$ is positive on
$\Psi_{\mu}$ is positive on  $\left({\rm ln}\frac{R_{0}}{|\nabla u|_{2}},{\rm ln}\frac{R_{1}}{|\nabla u|_{2}}\right)$. Combining
$\left({\rm ln}\frac{R_{0}}{|\nabla u|_{2}},{\rm ln}\frac{R_{1}}{|\nabla u|_{2}}\right)$. Combining ![]() $\Psi_{\mu}(-\infty)=0^{-}$ with
$\Psi_{\mu}(-\infty)=0^{-}$ with ![]() $\Psi_{\mu}(+\infty)=-\infty$, we have that
$\Psi_{\mu}(+\infty)=-\infty$, we have that ![]() $\Psi_{\mu}$ has at least two critical points. One is a local minimum point
$\Psi_{\mu}$ has at least two critical points. One is a local minimum point ![]() $s_{\mu}(u)$ on
$s_{\mu}(u)$ on  $\left(-\infty,{\rm ln}\frac{R_{0}}{|\nabla u|_{2}}\right)$ with
$\left(-\infty,{\rm ln}\frac{R_{0}}{|\nabla u|_{2}}\right)$ with ![]() $\Psi_{\mu}(s_{\mu}(u)) \lt 0$. And the other one is a global maximum point
$\Psi_{\mu}(s_{\mu}(u)) \lt 0$. And the other one is a global maximum point ![]() $t_{\mu}(u)$ with
$t_{\mu}(u)$ with ![]() $t_{\mu}(u) \gt s_{\mu}(u)$ and
$t_{\mu}(u) \gt s_{\mu}(u)$ and ![]() $\Psi_{\mu}(t_{\mu}(u)) \gt 0$. Let us check that there are no other critical points of
$\Psi_{\mu}(t_{\mu}(u)) \gt 0$. Let us check that there are no other critical points of ![]() $\Psi_{\mu}(s)$. Indeed the equality
$\Psi_{\mu}(s)$. Indeed the equality ![]() $\Psi_{\mu}'(s)=0$ shows that:
$\Psi_{\mu}'(s)=0$ shows that:
 \begin{equation*}\begin{aligned}0=&Q_{\mu}(s*u)=\Psi_{\mu}'(s)\\
=&(1+\gamma_{\theta})\mu e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{2s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau \gamma_{q} e^{q\gamma_{q}s}\int_{\mathbb{R}^{N}}|u|^{q}-\gamma_{p}e^{p\gamma_{p}s}\int_{\mathbb{R}^{N}}|u|^{p}\\
=&e^{q\gamma_{q}s}\left((1+\gamma_{\theta})\mu e^{(\theta+\theta\gamma_{\theta}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{(2-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}\right)\\
&+e^{q\gamma_{q}s}\left((2+N)e^{(2+N-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\tau \gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q}-\gamma_{p}e^{(p\gamma_{p}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{p}\right).
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}0=&Q_{\mu}(s*u)=\Psi_{\mu}'(s)\\
=&(1+\gamma_{\theta})\mu e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{2s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+(2+N)e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\\
&-\tau \gamma_{q} e^{q\gamma_{q}s}\int_{\mathbb{R}^{N}}|u|^{q}-\gamma_{p}e^{p\gamma_{p}s}\int_{\mathbb{R}^{N}}|u|^{p}\\
=&e^{q\gamma_{q}s}\left((1+\gamma_{\theta})\mu e^{(\theta+\theta\gamma_{\theta}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{(2-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}\right)\\
&+e^{q\gamma_{q}s}\left((2+N)e^{(2+N-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\tau \gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q}-\gamma_{p}e^{(p\gamma_{p}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{p}\right).
\end{aligned}
\end{equation*} Since ![]() $q\gamma_{q} \lt \theta\gamma_{\theta}$,
$q\gamma_{q} \lt \theta\gamma_{\theta}$, ![]() $q\gamma_{q} \lt 2$ and
$q\gamma_{q} \lt 2$ and ![]() $q\gamma_{q} \lt p\gamma_{p}$ when
$q\gamma_{q} \lt p\gamma_{p}$ when  $2 \lt q \lt 2+\frac{4}{N}$ and
$2 \lt q \lt 2+\frac{4}{N}$ and  $4+\frac{4}{N} \lt p\leq2^{*}$, then
$4+\frac{4}{N} \lt p\leq2^{*}$, then ![]() $0=Q_{\mu}(s*u)=0$ if only and if
$0=Q_{\mu}(s*u)=0$ if only and if
 \begin{equation}
\tau \gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q}=f_{\mu}(s),
\end{equation}
\begin{equation}
\tau \gamma_{q}\int_{\mathbb{R}^{N}}|u|^{q}=f_{\mu}(s),
\end{equation}where
 \begin{equation*}\begin{aligned}f_{\mu}(s)=&(1+\gamma_{\theta})\mu e^{(\theta+\theta\gamma_{\theta}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{(2-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
&+(2+N)e^{(2+N-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\gamma_{p}e^{(p\gamma_{p}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{p}.\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}f_{\mu}(s)=&(1+\gamma_{\theta})\mu e^{(\theta+\theta\gamma_{\theta}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+e^{(2-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|\nabla u|^{2}\\
&+(2+N)e^{(2+N-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}
-\gamma_{p}e^{(p\gamma_{p}-q\gamma_{q})s}\int_{\mathbb{R}^{N}}|u|^{p}.\end{aligned}
\end{equation*} But ![]() $f_{\mu}(s)$ has a unique maximum point, thus equation (5.7) has at most two solutions.
$f_{\mu}(s)$ has a unique maximum point, thus equation (5.7) has at most two solutions.
Hence we know that ![]() $\Psi_{\mu}$ has exactly two critical points
$\Psi_{\mu}$ has exactly two critical points ![]() $s_{\mu}(u)$ and
$s_{\mu}(u)$ and ![]() $t_{\mu}(u)$. We deduce from Proposition 2.1 that
$t_{\mu}(u)$. We deduce from Proposition 2.1 that ![]() $s_{\mu}(u)*u$,
$s_{\mu}(u)*u$, ![]() $t_{\mu}(u)*u\in \mathcal{Q}_{\mu}(a)$. Meanwhile,
$t_{\mu}(u)*u\in \mathcal{Q}_{\mu}(a)$. Meanwhile, ![]() $s*u\in \mathcal{Q}_{\mu}(a)$ implies
$s*u\in \mathcal{Q}_{\mu}(a)$ implies ![]() $s\in\{s_{\mu}(u), t_{\mu}(u)\}$. We also get that
$s\in\{s_{\mu}(u), t_{\mu}(u)\}$. We also get that  $\Psi_{\mu, s_{\mu}(u)*u}''(0)=\Psi_{\mu}''(s_{\mu}(u))\geq0$ by using the property of minimality. Since
$\Psi_{\mu, s_{\mu}(u)*u}''(0)=\Psi_{\mu}''(s_{\mu}(u))\geq0$ by using the property of minimality. Since  $\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, then
$\mathcal{Q}_{\mu}^{0}(a)=\emptyset$, then ![]() $s_{\mu}(u)*u\in \mathcal{Q}_{\mu}^{+}(a)$. In the same way
$s_{\mu}(u)*u\in \mathcal{Q}_{\mu}^{+}(a)$. In the same way ![]() $t_{\mu}(u)*u\in \mathcal{Q}_{\mu}^{-}(a)$.
$t_{\mu}(u)*u\in \mathcal{Q}_{\mu}^{-}(a)$.
Recalling the behaviour at infinity and the monotonicity of ![]() $\Psi_{\mu}$, we have that
$\Psi_{\mu}$, we have that ![]() $\Psi_{\mu}$ has exactly two zeros
$\Psi_{\mu}$ has exactly two zeros ![]() $c_{\mu}(u) \lt d_{\mu}(u)$ with
$c_{\mu}(u) \lt d_{\mu}(u)$ with ![]() $s_{\mu}(u) \lt c_{\mu}(u) \lt t_{\mu}(u) \lt d_{\mu}(u)$. Since
$s_{\mu}(u) \lt c_{\mu}(u) \lt t_{\mu}(u) \lt d_{\mu}(u)$. Since ![]() $\Psi_{\mu}$ is a C 2 function, then there are at least two inflection points. In the same way as before, it is not difficult to see that
$\Psi_{\mu}$ is a C 2 function, then there are at least two inflection points. In the same way as before, it is not difficult to see that ![]() $\Psi_{\mu}$ has exactly two inflection points. In particular,
$\Psi_{\mu}$ has exactly two inflection points. In particular, ![]() $\Psi_{\mu}$ is concave on
$\Psi_{\mu}$ is concave on ![]() $[t_{\mu}(u),+\infty)$, so
$[t_{\mu}(u),+\infty)$, so ![]() $t_{\mu}(u) \lt 0$ if and only if
$t_{\mu}(u) \lt 0$ if and only if ![]() $Q_{\mu}(u)=\Psi_{\mu}'(0) \lt 0$.
$Q_{\mu}(u)=\Psi_{\mu}'(0) \lt 0$.
We can apply the implicit function theorem on the C 1 function ![]() $\Phi_{\mu}(s,u):=\Psi_{\mu}'(s)$ to show that
$\Phi_{\mu}(s,u):=\Psi_{\mu}'(s)$ to show that ![]() $u\in S(a)\mapsto s_{\mu}(u)\in\mathbb{R}$ and
$u\in S(a)\mapsto s_{\mu}(u)\in\mathbb{R}$ and ![]() $u\in S(a)\mapsto t_{\mu}(u)\in\mathbb{R}$ are of class C 1. Indeed,
$u\in S(a)\mapsto t_{\mu}(u)\in\mathbb{R}$ are of class C 1. Indeed,
 \begin{equation*}\Phi_{\mu}(s_{\mu}(u),u)=0,\ \ \ \partial\Phi_{\mu}(s_{\mu}(u),u)=\Psi_{\mu}''(s_{\mu}(u)) \gt 0 \ \ \ {\rm and}\ \ \
\mathcal{Q}_{\mu}^{0}(a)=\emptyset.\end{equation*}
\begin{equation*}\Phi_{\mu}(s_{\mu}(u),u)=0,\ \ \ \partial\Phi_{\mu}(s_{\mu}(u),u)=\Psi_{\mu}''(s_{\mu}(u)) \gt 0 \ \ \ {\rm and}\ \ \
\mathcal{Q}_{\mu}^{0}(a)=\emptyset.\end{equation*} Then, it is not possible to pass with continuity from ![]() $\mathcal{Q}_{\mu}^{+}(a)$ to
$\mathcal{Q}_{\mu}^{+}(a)$ to ![]() $\mathcal{Q}_{\mu}^{-}(a)$. Hence
$\mathcal{Q}_{\mu}^{-}(a)$. Hence ![]() $u\in S(a)\mapsto s_{\mu}(u)$ is of class C 1. In the same way
$u\in S(a)\mapsto s_{\mu}(u)$ is of class C 1. In the same way ![]() $u\in S(a)\mapsto t_{\mu}(u)$ is of class C 1.
$u\in S(a)\mapsto t_{\mu}(u)$ is of class C 1.
5.2. Ground state critical point of  $I_{\mu}|_{S(a)}$
$I_{\mu}|_{S(a)}$
For any k > 0, we define the set:
 \begin{equation*}A_{k}:=\{u\in S(a): |\nabla u|_{2} \lt k\}\ \ \ {\rm and}\ \ \ m_{\mu}(a,\tau):=\inf\limits_{u\in A_{R_{0}}}I_{\mu}(u),\end{equation*}
\begin{equation*}A_{k}:=\{u\in S(a): |\nabla u|_{2} \lt k\}\ \ \ {\rm and}\ \ \ m_{\mu}(a,\tau):=\inf\limits_{u\in A_{R_{0}}}I_{\mu}(u),\end{equation*}then we have the following corollary.
Corollary 5.4. For any ![]() $0 \lt \mu\leq1$, we see that
$0 \lt \mu\leq1$, we see that ![]() $\mathcal{Q}_{\mu}^{+}(a)$ is contained in
$\mathcal{Q}_{\mu}^{+}(a)$ is contained in ![]() $A_{R_{0}}$, and
$A_{R_{0}}$, and
 \begin{equation*}\sup\limits_{u\in\mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u)\leq0\leq\inf\limits_{u\in\mathcal{Q}_{\mu}^{-}(a)}I_{\mu}(u).\end{equation*}
\begin{equation*}\sup\limits_{u\in\mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u)\leq0\leq\inf\limits_{u\in\mathcal{Q}_{\mu}^{-}(a)}I_{\mu}(u).\end{equation*}Lemma 5.5. For any ![]() $0 \lt \mu\leq1$, we have that:
$0 \lt \mu\leq1$, we have that:
 \begin{equation*}m_{\mu}(a,\tau)=\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u)=\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u).\end{equation*}
\begin{equation*}m_{\mu}(a,\tau)=\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u)=\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u).\end{equation*} And, there exists a small ξ > 0 such that  $m_{\mu}(a,\tau) \lt \inf\limits_{u\in\overline{A_{R_{0}}}\setminus A_{R_{0}-\xi}}I_{\mu}(u)$.
$m_{\mu}(a,\tau) \lt \inf\limits_{u\in\overline{A_{R_{0}}}\setminus A_{R_{0}-\xi}}I_{\mu}(u)$.
Proof. For any ![]() $0 \lt \mu\leq1$ and
$0 \lt \mu\leq1$ and ![]() $u\in A_{R_{0}}$, we have:
$u\in A_{R_{0}}$, we have:
 \begin{equation*}I_{\mu}(u)\geq E(u)\geq h(|\nabla u|_{2})\geq \min\limits_{t\in[0,R_{0}]}h(t) \gt -\infty,\end{equation*}
\begin{equation*}I_{\mu}(u)\geq E(u)\geq h(|\nabla u|_{2})\geq \min\limits_{t\in[0,R_{0}]}h(t) \gt -\infty,\end{equation*} then ![]() $m_{\mu}(a,\tau) \gt -\infty$. On the other hand, we get
$m_{\mu}(a,\tau) \gt -\infty$. On the other hand, we get ![]() $|\nabla (s*u)|_{2} \lt R_{0}$ for
$|\nabla (s*u)|_{2} \lt R_{0}$ for ![]() $s \lt \lt -1$. It shows that
$s \lt \lt -1$. It shows that ![]() $I_{\mu}(s*u) \lt 0$. Hence
$I_{\mu}(s*u) \lt 0$. Hence ![]() $m_{\mu}(a,\tau) \lt 0$.
$m_{\mu}(a,\tau) \lt 0$.
By Corollary 5.4 we have ![]() $\mathcal{Q}_{\mu}^{+}(a)\subset A_{R_{0}}$, then,
$\mathcal{Q}_{\mu}^{+}(a)\subset A_{R_{0}}$, then,
 \begin{equation*}m_{\mu}(a,\tau)\leq\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u).\end{equation*}
\begin{equation*}m_{\mu}(a,\tau)\leq\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u).\end{equation*} By Lemma 5.3 we know that if ![]() $u\in A_{R_{0}}$, then
$u\in A_{R_{0}}$, then ![]() $s_{\mu}(u)*u\in \mathcal{Q}_{\mu}^{+}(a)\subset A_{R_{0}}$, and
$s_{\mu}(u)*u\in \mathcal{Q}_{\mu}^{+}(a)\subset A_{R_{0}}$, and
which shows that
 \begin{equation*}\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u)\leq m_{\mu}(a,\tau).\end{equation*}
\begin{equation*}\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u)\leq m_{\mu}(a,\tau).\end{equation*} We can prove  $\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u)=\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u)$ by using
$\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u)=\inf\limits_{u\in \mathcal{Q}_{\mu}^{+}(a)}I_{\mu}(u)$ by using ![]() $I_{\mu}(u) \gt 0$ on
$I_{\mu}(u) \gt 0$ on ![]() $\mathcal{Q}_{\mu}^{-}(a)$, see Corollary 5.4.
$\mathcal{Q}_{\mu}^{-}(a)$, see Corollary 5.4.
Finally, there exists ρ > 0 such that  $h(t)\geq \frac{m_{\mu}(a,\tau)}{2}$ if
$h(t)\geq \frac{m_{\mu}(a,\tau)}{2}$ if ![]() $t\in [R_{0}-\rho,R_{0}]$, due to the continuity of h. Therefore, for any
$t\in [R_{0}-\rho,R_{0}]$, due to the continuity of h. Therefore, for any ![]() $u\in S(a)$ with
$u\in S(a)$ with ![]() $R_{0}\leq|\nabla u|_{2}\leq R_{0}$, we get
$R_{0}\leq|\nabla u|_{2}\leq R_{0}$, we get
 \begin{equation*}I_{\mu}(u)\geq E(u)\geq h(|\nabla u|_{2})\geq \frac{m_{\mu}(a,\tau)}{2} \gt m_{\mu}(a,\tau).\end{equation*}
\begin{equation*}I_{\mu}(u)\geq E(u)\geq h(|\nabla u|_{2})\geq \frac{m_{\mu}(a,\tau)}{2} \gt m_{\mu}(a,\tau).\end{equation*} Existence of a local minimizer. When N = 1, we take µ = 0 and the process is similar to the case of ![]() $N\geq2$, so we focus on the case
$N\geq2$, so we focus on the case ![]() $N\geq2$. For any
$N\geq2$. For any ![]() $0 \lt \mu\leq1$, we study a minimizing sequence
$0 \lt \mu\leq1$, we study a minimizing sequence ![]() $\{v_{n}\}$ for
$\{v_{n}\}$ for  $I_{\mu}|_{A_{R_{0}}}$. It is natural to suppose that
$I_{\mu}|_{A_{R_{0}}}$. It is natural to suppose that ![]() $v_{n}\in S_{r}(a)$ is radially decreasing for every n. Indeed for every n, if this is not true, we can replace vn with
$v_{n}\in S_{r}(a)$ is radially decreasing for every n. Indeed for every n, if this is not true, we can replace vn with ![]() $|v_{n}|^{*}$, where
$|v_{n}|^{*}$, where ![]() $|v_{n}|^{*}$ is the Schwarz rearrangement of
$|v_{n}|^{*}$ is the Schwarz rearrangement of ![]() $|v_{n}|$. Hence
$|v_{n}|$. Hence ![]() $|v_{n}|^{*}$ is a new function in
$|v_{n}|^{*}$ is a new function in ![]() $A_{R_{0}}$. Moreover,
$A_{R_{0}}$. Moreover, ![]() $I_{\mu}(|v_{n}|^{*})\leq I_{\mu}(v_{n})$. For every n we also have
$I_{\mu}(|v_{n}|^{*})\leq I_{\mu}(v_{n})$. For every n we also have ![]() $s_{\mu}(v_{n})*v_{n}\in \mathcal{Q}_{\mu}^{+}(a)$. We combine Lemma 5.3 with Corollary 5.4, then
$s_{\mu}(v_{n})*v_{n}\in \mathcal{Q}_{\mu}^{+}(a)$. We combine Lemma 5.3 with Corollary 5.4, then ![]() $|\nabla (s_{\mu}(v_{n})*v_{n})|_{2} \lt R_{0}$ and,
$|\nabla (s_{\mu}(v_{n})*v_{n})|_{2} \lt R_{0}$ and,
So we get a new minimizing sequence ![]() $\{w_{n}=s_{\mu}(v_{n})*v_{n}\}$ with the property that
$\{w_{n}=s_{\mu}(v_{n})*v_{n}\}$ with the property that ![]() $w_{n}\in S_{r}(a)\cap \mathcal{Q}_{\mu}^{+}(a)$ is radially decreasing for any n. By Lemma 5.5 we get for every n,
$w_{n}\in S_{r}(a)\cap \mathcal{Q}_{\mu}^{+}(a)$ is radially decreasing for any n. By Lemma 5.5 we get for every n,
Hence the Ekeland’s variational principle implies the existence of a new minimizing sequence ![]() $u_{n}\subset A_{R_{0}}$ for
$u_{n}\subset A_{R_{0}}$ for ![]() $m_{\mu}(a,\tau)$ in a standard way. Meanwhile,
$m_{\mu}(a,\tau)$ in a standard way. Meanwhile, ![]() $\{u_{n}\}$ has the additional property:
$\{u_{n}\}$ has the additional property:
which is also a P.S. sequence for ![]() $I_{\mu}|_{S(a)}$. Since
$I_{\mu}|_{S(a)}$. Since ![]() $\{w_{n}\}$ is bounded, then
$\{w_{n}\}$ is bounded, then ![]() $Q_{\mu}(u_{n})\rightarrow0$. By Lemma 3.2, up to a subsequence un such that:
$Q_{\mu}(u_{n})\rightarrow0$. By Lemma 3.2, up to a subsequence un such that:
where ![]() $u_{\mu,1}$ is an interior local minimizer for
$u_{\mu,1}$ is an interior local minimizer for  $I_{\mu}|_{A_{R_{0}}}$. By the maximum principle,
$I_{\mu}|_{A_{R_{0}}}$. By the maximum principle, ![]() $u_{\mu,1}$ is a positive function. To prove that
$u_{\mu,1}$ is a positive function. To prove that ![]() $u_{\mu,1}$ is a ground state for
$u_{\mu,1}$ is a ground state for ![]() $I_{\mu}|_{S(a)}$, we only use the fact that any critical point of
$I_{\mu}|_{S(a)}$, we only use the fact that any critical point of ![]() $I_{\mu}|_{S(a)}$ lies in
$I_{\mu}|_{S(a)}$ lies in ![]() $\mathcal{Q}_{\mu}(a)$, and
$\mathcal{Q}_{\mu}(a)$, and  $m_{\mu}(a,\tau)=\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u)$, see Lemma 5.5.
$m_{\mu}(a,\tau)=\inf\limits_{u\in \mathcal{Q}_{\mu}(a)}I_{\mu}(u)$, see Lemma 5.5.
5.3. The second critical point of  $I_{\mu}|_{S(a)}$
$I_{\mu}|_{S(a)}$
Lemma 5.6. For any ![]() $0 \lt \mu\leq1 $, assume that
$0 \lt \mu\leq1 $, assume that ![]() $I_{\mu}(u) \lt m_{\mu}(a,\tau)$, then
$I_{\mu}(u) \lt m_{\mu}(a,\tau)$, then ![]() $t_{\mu}(u) \lt 0$.
$t_{\mu}(u) \lt 0$.
Proof. Recalling the function ![]() $\Psi_{\mu}(s)$ and Lemma 5.3, we get:
$\Psi_{\mu}(s)$ and Lemma 5.3, we get:
so if ![]() $d_{\mu}(u)\leq0$, then
$d_{\mu}(u)\leq0$, then ![]() $t_{\mu}(u) \lt 0$. And we can assume that
$t_{\mu}(u) \lt 0$. And we can assume that ![]() $d_{\mu}(u) \gt 0$. We claim that
$d_{\mu}(u) \gt 0$. We claim that ![]() $0\not\in(c_{\mu}(u),d_{\mu}(u))$. Indeed if
$0\not\in(c_{\mu}(u),d_{\mu}(u))$. Indeed if ![]() $0\in(c_{\mu}(u),d_{\mu}(u))$, then
$0\in(c_{\mu}(u),d_{\mu}(u))$, then ![]() $I_{\mu}(u)=\Psi_{\mu}(0) \gt 0$, which contradicts with the fact
$I_{\mu}(u)=\Psi_{\mu}(0) \gt 0$, which contradicts with the fact ![]() $I_{\mu}(u) \lt m_{\mu}(a,\tau) \lt 0$. Hence
$I_{\mu}(u) \lt m_{\mu}(a,\tau) \lt 0$. Hence ![]() $c_{\mu}(u) \gt 0$. We get from Lemma 5.3-(2) that:
$c_{\mu}(u) \gt 0$. We get from Lemma 5.3-(2) that:
 \begin{equation*}
\begin{aligned}m_{\mu}(a,\tau)& \gt I_{\mu}(u)=\Psi_{\mu}(0)\geq \inf\limits_{s\in (-\infty,c_{\mu}(u)]}\Psi_{\mu}(s)\\
&\geq\inf\{I_{\mu}(s*u): s\in\mathbb{R} \ {\rm and} \ |\nabla (s*u)|_{2} \lt R_{0} \}=I_{\mu}(s_{\mu}(u)*u)\geq m_{\mu}(a,\tau),
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}m_{\mu}(a,\tau)& \gt I_{\mu}(u)=\Psi_{\mu}(0)\geq \inf\limits_{s\in (-\infty,c_{\mu}(u)]}\Psi_{\mu}(s)\\
&\geq\inf\{I_{\mu}(s*u): s\in\mathbb{R} \ {\rm and} \ |\nabla (s*u)|_{2} \lt R_{0} \}=I_{\mu}(s_{\mu}(u)*u)\geq m_{\mu}(a,\tau),
\end{aligned}
\end{equation*}which is also a contradiction.
Lemma 5.7. For any ![]() $0 \lt \mu\leq1 $, we have
$0 \lt \mu\leq1 $, we have  $\widetilde{\sigma}_{\mu}(a,\tau):=\inf\limits_{u\in\mathcal{Q}_{\mu}^{-}(a)}I_{\mu}(u) \gt 0$.
$\widetilde{\sigma}_{\mu}(a,\tau):=\inf\limits_{u\in\mathcal{Q}_{\mu}^{-}(a)}I_{\mu}(u) \gt 0$.
Proof. Recalling the properties of the function h, we can assume that tmax is the strict maximum point of the function h with ![]() $h(t_{max}) \gt 0$.
$h(t_{max}) \gt 0$.
For any ![]() $0 \lt \mu\leq1$ and
$0 \lt \mu\leq1$ and ![]() $u\in\mathcal{Q}_{\mu}^{-}(a)$, there exists
$u\in\mathcal{Q}_{\mu}^{-}(a)$, there exists ![]() $\omega_{\mu}(u)\in\mathbb{R}$, such that
$\omega_{\mu}(u)\in\mathbb{R}$, such that ![]() $|\nabla(\omega_{\mu}(u))*u)|_{2}=t_{max}$. Furthermore, by Lemma 5.3 and the fact
$|\nabla(\omega_{\mu}(u))*u)|_{2}=t_{max}$. Furthermore, by Lemma 5.3 and the fact ![]() $u\in\mathcal{Q}_{\mu}^{-}(a)$, then 0 is the unique strict maximum of the function
$u\in\mathcal{Q}_{\mu}^{-}(a)$, then 0 is the unique strict maximum of the function ![]() $\Psi_{\mu}$. Thus,
$\Psi_{\mu}$. Thus,
 \begin{align*}I_{\mu}(u)& =\Psi_{\mu}(0)\geq\Psi_{\mu}(\omega_{\mu}(u))=I_{\mu}(\omega_{\mu}(u)*u)\geq E(\omega_{\mu}(u)*u)\geq h(|\nabla(\omega_{\mu}(u))*u)|_{2})\nonumber \\ & \qquad =h(t_{max}) \gt 0.\end{align*}
\begin{align*}I_{\mu}(u)& =\Psi_{\mu}(0)\geq\Psi_{\mu}(\omega_{\mu}(u))=I_{\mu}(\omega_{\mu}(u)*u)\geq E(\omega_{\mu}(u)*u)\geq h(|\nabla(\omega_{\mu}(u))*u)|_{2})\nonumber \\ & \qquad =h(t_{max}) \gt 0.\end{align*} Since ![]() $u\in\mathcal{Q}_{\mu}^{-}(a)$ is arbitrary, then we conclude that
$u\in\mathcal{Q}_{\mu}^{-}(a)$ is arbitrary, then we conclude that  $\inf\limits_{u\in\mathcal{Q}_{\mu}^{-}(a)}I_{\mu}(u)\geq \max\limits_{t\in\mathbb{R}}h(t) \gt 0$.
$\inf\limits_{u\in\mathcal{Q}_{\mu}^{-}(a)}I_{\mu}(u)\geq \max\limits_{t\in\mathbb{R}}h(t) \gt 0$.
Existence of a second critical point of mountain pass type for ![]() $I_{\mu}|_{S(a)}$.
$I_{\mu}|_{S(a)}$.
When N = 1, we take µ = 0 and the process is similar to the case of ![]() $N\geq2$, so we focus on the case
$N\geq2$, so we focus on the case ![]() $N\geq2$.
$N\geq2$.
In the same way in ![]() $\S$ 4, we consider the augmented functional
$\S$ 4, we consider the augmented functional ![]() $\widetilde{I_{\mu}}$:
$\widetilde{I_{\mu}}$:
 \begin{align}
\widetilde{I_{\mu}}(s,u):=&I_{\mu}(s*u)\nonumber\\
&=\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\nonumber \\
& \qquad -\frac{\tau}{q}e^{q\gamma_{q}s}\int_{\mathbb{R}^{N}}|u|^{q} -\frac{1}{p}e^{p\gamma_{p}s}\int_{\mathbb{R}^{N}}|u|^{p}.
\end{align}
\begin{align}
\widetilde{I_{\mu}}(s,u):=&I_{\mu}(s*u)\nonumber\\
&=\frac{\mu}{\theta}e^{\theta(1+\gamma_{\theta})s}\int_{\mathbb{R}^{N}}|\nabla u|^{\theta}+\frac{e^{2s}}{2}\int_{\mathbb{R}^{N}}|\nabla u|^{2}+e^{(2+N)s}\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2}\nonumber \\
& \qquad -\frac{\tau}{q}e^{q\gamma_{q}s}\int_{\mathbb{R}^{N}}|u|^{q} -\frac{1}{p}e^{p\gamma_{p}s}\int_{\mathbb{R}^{N}}|u|^{p}.
\end{align} Denoting by ![]() $I_{\mu}^{c}$ the closed sublevel set
$I_{\mu}^{c}$ the closed sublevel set ![]() $\{u\in S(a): I_{\mu}(u)\leq c \}$, we introduce the minimax class:
$\{u\in S(a): I_{\mu}(u)\leq c \}$, we introduce the minimax class:
 \begin{equation*}\Gamma:=\{\gamma(\tau)=(\alpha,\beta)\in C([0,1],\mathbb{R}\times S_{r}(a)):
\ \gamma(0)\in (0,\mathcal{Q}_{\mu}^{+}),\ \gamma(1)\in (0,I_{\mu}^{2m_{\mu}(a,\tau)})\},\end{equation*}
\begin{equation*}\Gamma:=\{\gamma(\tau)=(\alpha,\beta)\in C([0,1],\mathbb{R}\times S_{r}(a)):
\ \gamma(0)\in (0,\mathcal{Q}_{\mu}^{+}),\ \gamma(1)\in (0,I_{\mu}^{2m_{\mu}(a,\tau)})\},\end{equation*}with associated minimax level:
 \begin{equation*}\sigma_{\mu}(a,\tau):=\inf\limits_{\gamma\in \Gamma}\max\limits_{(s,u)\in \gamma([0,1])}\widetilde{I}_{\mu}(s,u).\end{equation*}
\begin{equation*}\sigma_{\mu}(a,\tau):=\inf\limits_{\gamma\in \Gamma}\max\limits_{(s,u)\in \gamma([0,1])}\widetilde{I}_{\mu}(s,u).\end{equation*} For any ![]() $0 \lt \mu\leq1$ and
$0 \lt \mu\leq1$ and ![]() $u\in S_{r}(a)$. By Lemma 5.3 there exists
$u\in S_{r}(a)$. By Lemma 5.3 there exists ![]() $s_{1} \gt \gt 1$ such that:
$s_{1} \gt \gt 1$ such that:
is a path in Γ. Hence the minimax value ![]() $\sigma_{\mu}(a,\tau)$ is a real number.
$\sigma_{\mu}(a,\tau)$ is a real number.
We claim that ![]() $\forall \gamma\in \Gamma$, there exists
$\forall \gamma\in \Gamma$, there exists ![]() $\chi_{\gamma}\in (0,1)$ such that
$\chi_{\gamma}\in (0,1)$ such that ![]() $\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}^{-}(a)$. Indeed, since
$\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}^{-}(a)$. Indeed, since ![]() $\gamma(0)=(\alpha(0),\beta(0))\in (0,\mathcal{Q}_{\mu}^{+}(a))$, we have:
$\gamma(0)=(\alpha(0),\beta(0))\in (0,\mathcal{Q}_{\mu}^{+}(a))$, we have:
Since  $I_{\mu}(\beta(1))=\widetilde{I}_{\mu}(\beta(1))=\widetilde{I}_{\mu}(\gamma(1)) \lt 2m_{\mu}(a,\tau)$, we deduce from Proposition 2.1 and Lemma 5.3 that:
$I_{\mu}(\beta(1))=\widetilde{I}_{\mu}(\beta(1))=\widetilde{I}_{\mu}(\gamma(1)) \lt 2m_{\mu}(a,\tau)$, we deduce from Proposition 2.1 and Lemma 5.3 that:
and the map ![]() $t_{\alpha(\chi)*\beta(\chi)}$ is continuous in Γ. It is not difficult to show that for any
$t_{\alpha(\chi)*\beta(\chi)}$ is continuous in Γ. It is not difficult to show that for any ![]() $\gamma\in \Gamma$, there exists
$\gamma\in \Gamma$, there exists ![]() $\chi_{\gamma}\in (0,1)$ such that
$\chi_{\gamma}\in (0,1)$ such that ![]() $t_{\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})}=0$, in the sense that
$t_{\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})}=0$, in the sense that ![]() $\alpha(\tau_{\gamma})*\beta(\tau_{\gamma})\in \mathcal{Q}_{\mu}^{-}(a)$.
$\alpha(\tau_{\gamma})*\beta(\tau_{\gamma})\in \mathcal{Q}_{\mu}^{-}(a)$.
For any ![]() $\gamma\in \Gamma$, we get from
$\gamma\in \Gamma$, we get from ![]() $\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}^{-}(a)$ that:
$\alpha(\chi_{\gamma})*\beta(\chi_{\gamma})\in \mathcal{Q}_{\mu}^{-}(a)$ that:
 \begin{equation*}\max\limits_{\gamma([0,1])}\widetilde{I}_{\mu}\geq\widetilde{I}_{\mu}(\gamma(\chi_{\gamma}))=I_{\mu}(\alpha(\chi_{\gamma})*\beta(\chi_{\gamma}))\geq \inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu},\end{equation*}
\begin{equation*}\max\limits_{\gamma([0,1])}\widetilde{I}_{\mu}\geq\widetilde{I}_{\mu}(\gamma(\chi_{\gamma}))=I_{\mu}(\alpha(\chi_{\gamma})*\beta(\chi_{\gamma}))\geq \inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu},\end{equation*} which shows that  $\sigma_{\mu}(a,\tau)\geq \inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu}$. On the other hand, if
$\sigma_{\mu}(a,\tau)\geq \inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu}$. On the other hand, if ![]() $u\in \mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)$, then γu defined in (5.10) is a path in Γ with:
$u\in \mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)$, then γu defined in (5.10) is a path in Γ with:
 \begin{equation*}I_{\mu}(u)=\widetilde{I}_{\mu}(0,u)=\max\limits_{\gamma_{u}([0,1])}\widetilde{I}_{\mu}\geq \sigma_{\mu}(a,\tau),\end{equation*}
\begin{equation*}I_{\mu}(u)=\widetilde{I}_{\mu}(0,u)=\max\limits_{\gamma_{u}([0,1])}\widetilde{I}_{\mu}\geq \sigma_{\mu}(a,\tau),\end{equation*} which gives  $\inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu}\geq \sigma_{\mu}(a,\tau)$. Thus
$\inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu}\geq \sigma_{\mu}(a,\tau)$. Thus  $\sigma_{\mu}(a,\tau)=\inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu}$.
$\sigma_{\mu}(a,\tau)=\inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu}$.
And Corollary 5.4 and Lemma 5.7 imply that:
 \begin{align*}
& \sigma_{\mu}(a,\tau)=\inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu} \gt 0\geq
\sup\limits_{(\mathcal{Q}_{\mu}^{-}(a)\cup I_{\mu}^{2m_{\mu}(a,\tau)})\cap S_{r}(a)}\nonumber\\
& \qquad I_{\mu}=\sup\limits_{((0,\mathcal{Q}_{\mu}^{-}(a))\cup (0,I_{\mu}^{2m_{\mu}(a,\tau)}))\cap S_{r}(a)}I_{\mu}.\end{align*}
\begin{align*}
& \sigma_{\mu}(a,\tau)=\inf\limits_{\mathcal{Q}_{\mu}^{-}(a)\cap S_{r}(a)}I_{\mu} \gt 0\geq
\sup\limits_{(\mathcal{Q}_{\mu}^{-}(a)\cup I_{\mu}^{2m_{\mu}(a,\tau)})\cap S_{r}(a)}\nonumber\\
& \qquad I_{\mu}=\sup\limits_{((0,\mathcal{Q}_{\mu}^{-}(a))\cup (0,I_{\mu}^{2m_{\mu}(a,\tau)}))\cap S_{r}(a)}I_{\mu}.\end{align*} By using the terminology in Section 5 [Reference Ghoussoub17], we get that ![]() $\{\gamma([0,1]):\gamma\in\Gamma\}$ is a homotopic stable family with extended closed boundary
$\{\gamma([0,1]):\gamma\in\Gamma\}$ is a homotopic stable family with extended closed boundary  $(0,\mathcal{Q}_{\mu}^{+}(a))\cup(0,I_{\mu}^{0})$, where
$(0,\mathcal{Q}_{\mu}^{+}(a))\cup(0,I_{\mu}^{0})$, where ![]() $\gamma([0,1])$ is the compact subset of
$\gamma([0,1])$ is the compact subset of ![]() $\mathbb{R}\times S_{r}(a)$. We also deduce that the superlevel set
$\mathbb{R}\times S_{r}(a)$. We also deduce that the superlevel set  $\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a,\tau)\}$ is a dual set, that is,
$\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a,\tau)\}$ is a dual set, that is,  $\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a,\tau)\}$ satisfies the assumptions (F’1) and (F’2) in Theorem 5.2 [Reference Ghoussoub17]. Hence, we can take any minimizing sequence
$\{\widetilde{I}_{\mu}\geq\sigma_{\mu}(a,\tau)\}$ satisfies the assumptions (F’1) and (F’2) in Theorem 5.2 [Reference Ghoussoub17]. Hence, we can take any minimizing sequence ![]() $\{\gamma_{n}=(\alpha_{n},\beta_{n})\}\subset\Gamma$ for
$\{\gamma_{n}=(\alpha_{n},\beta_{n})\}\subset\Gamma$ for ![]() $\sigma_{\mu}(a,\tau)$ with the additional properties that
$\sigma_{\mu}(a,\tau)$ with the additional properties that ![]() $\alpha_{n}\equiv0$ and
$\alpha_{n}\equiv0$ and ![]() $\beta_{n}\geq0$ a.e. on
$\beta_{n}\geq0$ a.e. on ![]() $\mathbb{R}^{N}$ for every
$\mathbb{R}^{N}$ for every ![]() $\chi\in[0,1]$, there exists a P.S. sequence
$\chi\in[0,1]$, there exists a P.S. sequence ![]() $\{(s_{n},w_{n})\}\subset\mathbb{R}\times S_{r}(a)$ for
$\{(s_{n},w_{n})\}\subset\mathbb{R}\times S_{r}(a)$ for  $\widetilde{I}_{\mu}|_{\mathbb{R}\times S_{r}(a)}$ at level
$\widetilde{I}_{\mu}|_{\mathbb{R}\times S_{r}(a)}$ at level ![]() $\sigma_{\mu}(a,\tau)$, in the sense that:
$\sigma_{\mu}(a,\tau)$, in the sense that:
 \begin{equation}
\partial_{s}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0 \ \ \ {\rm and}\ \ \ \partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,
\end{equation}
\begin{equation}
\partial_{s}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0 \ \ \ {\rm and}\ \ \ \partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,
\end{equation}with the property that
By (5.9) and (5.11), we get ![]() $Q_{\mu}(s_{n}*w_{n})\rightarrow0$ and,
$Q_{\mu}(s_{n}*w_{n})\rightarrow0$ and,
 \begin{equation*}\|\partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\|_{(T_{w_{n}}S_{r}(a))^{*}}\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,\end{equation*}
\begin{equation*}\|\partial_{u}\widetilde{I}_{\mu}(s_{n},w_{n})\|_{(T_{w_{n}}S_{r}(a))^{*}}\rightarrow0\ \ \ {\rm as}\ n\rightarrow\infty,\end{equation*} Since ![]() $\{s_{n}\}$ is bounded, due to (5.12), this is equivalent to:
$\{s_{n}\}$ is bounded, due to (5.12), this is equivalent to:
Let then ![]() $u_{n}:=s_{n}*w_{n}$. By Lemma 4.7 equation (5.13) establishes that
$u_{n}:=s_{n}*w_{n}$. By Lemma 4.7 equation (5.13) establishes that ![]() $\{u_{n}\}\subset S_{r}(a)$ is a P.S. sequence for
$\{u_{n}\}\subset S_{r}(a)$ is a P.S. sequence for ![]() $I_{\mu}|_{S_{r}(a)}$ at level
$I_{\mu}|_{S_{r}(a)}$ at level ![]() $\sigma_{\mu}(a,\tau) \gt 0$ with
$\sigma_{\mu}(a,\tau) \gt 0$ with ![]() $Q_{\mu}(u_{n})\rightarrow0$. Thus, it is also a P.S. sequence for
$Q_{\mu}(u_{n})\rightarrow0$. Thus, it is also a P.S. sequence for ![]() $I_{\mu}|_{S(a)}$ at level
$I_{\mu}|_{S(a)}$ at level ![]() $\sigma_{\mu}(a,\tau) \gt 0$ with
$\sigma_{\mu}(a,\tau) \gt 0$ with ![]() $Q_{\mu}(u_{n})\rightarrow0$, because the problem is invariant under rotations. We deduce from Lemma 3.1 that, up to a subsequence such that
$Q_{\mu}(u_{n})\rightarrow0$, because the problem is invariant under rotations. We deduce from Lemma 3.1 that, up to a subsequence such that ![]() $u_{n}\rightarrow \overline{u}_{\mu}$ in
$u_{n}\rightarrow \overline{u}_{\mu}$ in ![]() $\mathcal{X}$, where
$\mathcal{X}$, where ![]() $\overline{u}_{\mu}\in S(a)$ is a radially symmetric and real function. From (32) we have that
$\overline{u}_{\mu}\in S(a)$ is a radially symmetric and real function. From (32) we have that ![]() $\overline{u}_{\mu}\geq0$ a.e. on
$\overline{u}_{\mu}\geq0$ a.e. on ![]() $\mathbb{R}^{N}$, and the strong maximum principle implies that
$\mathbb{R}^{N}$, and the strong maximum principle implies that ![]() $\overline{u}_{\mu} \gt 0$.
$\overline{u}_{\mu} \gt 0$.
6. Convergence issues as  $\mu\rightarrow0^{+}$
$\mu\rightarrow0^{+}$
In this section we will give the proof of the convergence for the sequences of critical points of ![]() $I_{\mu}|_{S(a)}$ achieved in
$I_{\mu}|_{S(a)}$ achieved in ![]() $\S$ 4 and
$\S$ 4 and ![]() $\S$ 5 as
$\S$ 5 as ![]() $\mu\rightarrow0^{+}$.
$\mu\rightarrow0^{+}$.
Lemma 6.1. Let ![]() $N\geq2$. Suppose that one of the following conditions holds
$N\geq2$. Suppose that one of the following conditions holds
(a) f(u) satisfies (F1) and (F2).
(b) ![]() $f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2).
$f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2).
Assume that ![]() $\mu_{n}\rightarrow 0^{+}$,
$\mu_{n}\rightarrow 0^{+}$, ![]() $I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0 \ {\rm with}\ \lambda_{\mu_{n}}\geq0 \ {\rm and}\
I_{\mu_{n}}(u_{\mu_{n}})\rightarrow c\neq0$ for
$I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0 \ {\rm with}\ \lambda_{\mu_{n}}\geq0 \ {\rm and}\
I_{\mu_{n}}(u_{\mu_{n}})\rightarrow c\neq0$ for ![]() $u_{\mu_{n}}\in S_{r}(a_{n})$ with
$u_{\mu_{n}}\in S_{r}(a_{n})$ with ![]() $0 \lt a_{n}\leq a$. Then up to a sequence, there exists a
$0 \lt a_{n}\leq a$. Then up to a sequence, there exists a  $u\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with u ≠ 0 such that
$u\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with u ≠ 0 such that ![]() $u_{\mu_{n}}\rightharpoonup u$ in
$u_{\mu_{n}}\rightharpoonup u$ in ![]() $W^{1,2}(\mathbb{R}^{N})$ and there exists a
$W^{1,2}(\mathbb{R}^{N})$ and there exists a ![]() $\lambda\in \mathbb{R}$ such that:
$\lambda\in \mathbb{R}$ such that:
 \begin{equation*}I_{\mu}'(u)+\lambda u=0,\ \ \ I(u)=c\ \ \ {\rm and}\ \ \ 0 \lt |u|_{2}^{2}\leq a.\end{equation*}
\begin{equation*}I_{\mu}'(u)+\lambda u=0,\ \ \ I(u)=c\ \ \ {\rm and}\ \ \ 0 \lt |u|_{2}^{2}\leq a.\end{equation*}Moreover,
(1) if ![]() $u_{\mu_{n}}\geq 0$ for any
$u_{\mu_{n}}\geq 0$ for any ![]() $n\in \mathbb{N}^{+}$, then
$n\in \mathbb{N}^{+}$, then ![]() $u\geq 0$,
$u\geq 0$,
(2) if λ ≠ 0, then  $|u|_{2}^{2}=\lim\limits_{n\rightarrow \infty }a_{n}$.
$|u|_{2}^{2}=\lim\limits_{n\rightarrow \infty }a_{n}$.
Proof. The proof is motivated by [Reference Jeanjean, Le and Wang19, Reference Li, Wang, Teng and Wu24]. Since any critical point of ![]() $I_{\mu}|_{S(a)}$ is contained in
$I_{\mu}|_{S(a)}$ is contained in ![]() $\mathcal{Q}_{\mu}(a)$, then
$\mathcal{Q}_{\mu}(a)$, then ![]() $I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$ implies that:
$I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$ implies that:
By the Step 1 of Lemma 3.1, we get
 \begin{equation}
\sup\limits_{n\geq1}\max\left\{\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta},\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{2},\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2}|\nabla u_{\mu_{n}}|^{2} \right\} \lt +\infty,
\end{equation}
\begin{equation}
\sup\limits_{n\geq1}\max\left\{\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta},\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{2},\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2}|\nabla u_{\mu_{n}}|^{2} \right\} \lt +\infty,
\end{equation} and thus ![]() $u_{\mu_{n}}$ is bounded in
$u_{\mu_{n}}$ is bounded in ![]() $W^{1,2}(\mathbb{R}^{N})$. We claim that
$W^{1,2}(\mathbb{R}^{N})$. We claim that  $\liminf\limits_{n\rightarrow\infty} a_{n} \gt 0$. Indeed, if
$\liminf\limits_{n\rightarrow\infty} a_{n} \gt 0$. Indeed, if ![]() $a_{n}\rightarrow 0$, then,
$a_{n}\rightarrow 0$, then,
 \begin{equation*}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})u_{\mu_{n}}\rightarrow 0,\ \ \ \int_{\mathbb{R}^{N}}F(u_{\mu_{n}})\rightarrow 0,\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})u_{\mu_{n}}\rightarrow 0,\ \ \ \int_{\mathbb{R}^{N}}F(u_{\mu_{n}})\rightarrow 0,\end{equation*} and we deduce from ![]() $Q_{\mu_{n}}(u_{\mu_{n}})=0$ that
$Q_{\mu_{n}}(u_{\mu_{n}})=0$ that ![]() $I_{\mu_{n}}(u_{\mu_{n}})\rightarrow 0$ which contradicts with c ≠ 0. Hence
$I_{\mu_{n}}(u_{\mu_{n}})\rightarrow 0$ which contradicts with c ≠ 0. Hence  $\lambda_{n}=-\frac{1}{a_{n}^{2}}I_{\mu}'(u_{n})[u_{n}]$ is bounded in
$\lambda_{n}=-\frac{1}{a_{n}^{2}}I_{\mu}'(u_{n})[u_{n}]$ is bounded in ![]() $\mathbb{R}$. Then up to a subsequence, there exists a
$\mathbb{R}$. Then up to a subsequence, there exists a ![]() $\lambda\in\mathbb{R}$ such that
$\lambda\in\mathbb{R}$ such that ![]() $\lambda_{\mu_{n}}\rightarrow \lambda$ in
$\lambda_{\mu_{n}}\rightarrow \lambda$ in ![]() $\mathbb{R}.$ And, there also exists a
$\mathbb{R}.$ And, there also exists a ![]() $u\in W^{1,2}(\mathbb{R}^{N})$ with
$u\in W^{1,2}(\mathbb{R}^{N})$ with ![]() $u\not\equiv0$ such that:
$u\not\equiv0$ such that:
 \begin{equation*}u_{\mu_{n}}\rightharpoonup u\ \ \ {\rm in} \ W^{1,2}(\mathbb{R}^{N}),\end{equation*}
\begin{equation*}u_{\mu_{n}}\rightharpoonup u\ \ \ {\rm in} \ W^{1,2}(\mathbb{R}^{N}),\end{equation*} \begin{equation*}u_{\mu_{n}}\rightarrow u\ \ \ {\rm in}\ L^{r}(\mathbb{R}^{N}),\ \forall r \in(2,2\cdot2^{*}),\end{equation*}
\begin{equation*}u_{\mu_{n}}\rightarrow u\ \ \ {\rm in}\ L^{r}(\mathbb{R}^{N}),\ \forall r \in(2,2\cdot2^{*}),\end{equation*} \begin{equation*}u_{\mu_{n}}\rightarrow u\ \ \ {\rm a.e.}\ {\rm on}\ \mathbb{R}^{N}.\end{equation*}
\begin{equation*}u_{\mu_{n}}\rightarrow u\ \ \ {\rm a.e.}\ {\rm on}\ \mathbb{R}^{N}.\end{equation*} So, the condition ![]() $u_{\mu_{n}}\geq 0$ for any
$u_{\mu_{n}}\geq 0$ for any ![]() $n\in\mathbb{N}^{+}$ implies that
$n\in\mathbb{N}^{+}$ implies that ![]() $u\geq 0$. Moreover, we have that:
$u\geq 0$. Moreover, we have that:
 \begin{equation*}u_{\mu_{n}}\nabla u_{\mu_{n}}\rightarrow u\nabla u \ {\rm in}\ \left(L_{loc}^{2}(\mathbb{R}^{N})\right)^{N}
\ \ \ {\rm and}\ \ \ \nabla u_{\mu_{n}}\rightarrow\nabla u \ {\rm a.e. \ on} \ \mathbb{R}^{N},\end{equation*}
\begin{equation*}u_{\mu_{n}}\nabla u_{\mu_{n}}\rightarrow u\nabla u \ {\rm in}\ \left(L_{loc}^{2}(\mathbb{R}^{N})\right)^{N}
\ \ \ {\rm and}\ \ \ \nabla u_{\mu_{n}}\rightarrow\nabla u \ {\rm a.e. \ on} \ \mathbb{R}^{N},\end{equation*}see Lemma A.2 [Reference Li and Zou23] for more details. Here we give the proof in three steps.
Step 1. There exists a constant C > 0 such that ![]() $\|u_{\mu_{n}}\|_{\infty}\leq C$ and
$\|u_{\mu_{n}}\|_{\infty}\leq C$ and ![]() $\|u\|_{\infty}\leq C$.
$\|u\|_{\infty}\leq C$.
The proof of the case N = 2 is similar to ![]() $N\geq3$, then we only prove the case
$N\geq3$, then we only prove the case ![]() $N\geq3$. Let T > 2, r > 0 and
$N\geq3$. Let T > 2, r > 0 and
 \begin{equation*}v_{n}=\left\{\begin{aligned} &T, \ \ \ \ \ \ u_{\mu_{n}}\geq T,\\
&u_{\mu_{n}}, \ \ \ \ |u_{\mu_{n}}|\leq T,\\
&-T, \ \ \ u_{\mu_{n}}\leq -T.
\end{aligned}
\right.\end{equation*}
\begin{equation*}v_{n}=\left\{\begin{aligned} &T, \ \ \ \ \ \ u_{\mu_{n}}\geq T,\\
&u_{\mu_{n}}, \ \ \ \ |u_{\mu_{n}}|\leq T,\\
&-T, \ \ \ u_{\mu_{n}}\leq -T.
\end{aligned}
\right.\end{equation*} Assume ![]() $\phi=u_{\mu_{n}}|v_{n}|^{2r}$, then
$\phi=u_{\mu_{n}}|v_{n}|^{2r}$, then ![]() $\phi\in \mathcal{X}$. Since
$\phi\in \mathcal{X}$. Since
 \begin{equation*}I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0\ \ \ {\rm and}\ \ \ \lambda_{\mu_{n}}\geq0,\end{equation*}
\begin{equation*}I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0\ \ \ {\rm and}\ \ \ \lambda_{\mu_{n}}\geq0,\end{equation*}then we have:
 \begin{equation*}\begin{aligned}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\phi=&\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}\cdot\nabla\phi
+\int_{\mathbb{R}^{N}}\nabla u_{\mu_{n}}\cdot\nabla\phi\\
&+2\int_{\mathbb{R}^{N}}\left(u_{\mu_{n}}\phi|\nabla u_{\mu_{n}}|^{2}+|u_{\mu_{n}}|^{2}\nabla u_{\mu_{n}}\cdot\nabla\phi\right)
+\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\phi\\
\geq& 2\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2}\nabla u_{\mu_{n}}\cdot\nabla\phi\\
=&2\int_{\mathbb{R}^{N}}\left(|u_{\mu_{n}}|^{2}|\nabla u_{\mu_{n}}|^{2}|v_{n}|^{2r}
+|u_{\mu_{n}}|^{2}2r|v_{n}|^{2r-2}u_{\mu_{n}}v_{n}\nabla u_{\mu_{n}}\cdot\nabla v_{n}\right)\\
=&\frac{1}{2}\int_{\mathbb{R}^{N}}\left||v_{n}|^{r}\nabla u_{\mu_{n}}^{2}\right|^{2}
+\frac{4}{r}\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}\nabla |v_{n}|^{r}\right|^{2}\\
\geq& \frac{1}{r+4}\int_{\mathbb{R}^{N}}\left|\nabla \left(u_{\mu_{n}}^{2}|v_{n}|^{r}\right)\right|^{2}
\geq \frac{C}{(r+2)^{2}}\left(\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}|v_{n}|^{r}\right|^{2^{*}}\right)^{\frac{2}{2^{*}}}.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\phi=&\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}\cdot\nabla\phi
+\int_{\mathbb{R}^{N}}\nabla u_{\mu_{n}}\cdot\nabla\phi\\
&+2\int_{\mathbb{R}^{N}}\left(u_{\mu_{n}}\phi|\nabla u_{\mu_{n}}|^{2}+|u_{\mu_{n}}|^{2}\nabla u_{\mu_{n}}\cdot\nabla\phi\right)
+\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\phi\\
\geq& 2\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2}\nabla u_{\mu_{n}}\cdot\nabla\phi\\
=&2\int_{\mathbb{R}^{N}}\left(|u_{\mu_{n}}|^{2}|\nabla u_{\mu_{n}}|^{2}|v_{n}|^{2r}
+|u_{\mu_{n}}|^{2}2r|v_{n}|^{2r-2}u_{\mu_{n}}v_{n}\nabla u_{\mu_{n}}\cdot\nabla v_{n}\right)\\
=&\frac{1}{2}\int_{\mathbb{R}^{N}}\left||v_{n}|^{r}\nabla u_{\mu_{n}}^{2}\right|^{2}
+\frac{4}{r}\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}\nabla |v_{n}|^{r}\right|^{2}\\
\geq& \frac{1}{r+4}\int_{\mathbb{R}^{N}}\left|\nabla \left(u_{\mu_{n}}^{2}|v_{n}|^{r}\right)\right|^{2}
\geq \frac{C}{(r+2)^{2}}\left(\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}|v_{n}|^{r}\right|^{2^{*}}\right)^{\frac{2}{2^{*}}}.
\end{aligned}
\end{equation*}Now, for the case of (a), f(u) satisfies (F1) and (F2), then
 \begin{align*}
& \int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\phi =\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})u_{\mu_{n}}|v_{n}|^{2r}
\leq\int_{\mathbb{R}^{N}}\beta F(u_{\mu_{n}})|v_{n}|^{2r}\\
& \qquad\qquad \leq \beta F(1)\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\alpha}|v_{n}|^{2r}
+\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\beta}|v_{n}|^{2r}\right).
\end{align*}
\begin{align*}
& \int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\phi =\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})u_{\mu_{n}}|v_{n}|^{2r}
\leq\int_{\mathbb{R}^{N}}\beta F(u_{\mu_{n}})|v_{n}|^{2r}\\
& \qquad\qquad \leq \beta F(1)\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\alpha}|v_{n}|^{2r}
+\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\beta}|v_{n}|^{2r}\right).
\end{align*}On the other hand, by the interpolation inequality, we have:
 \begin{align*}
&\quad \left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\alpha}|v_{n}|^{2r})
+(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\beta}|v_{n}|^{2r}\right)\\
&\quad\leq \left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{\alpha-4}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}}\right)^{\frac{2\cdot2^{*}-\alpha+4}{2\cdot2^{*}}}\\
& \quad+\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{\beta-4}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}}\right)^{\frac{2\cdot2^{*}-\beta+4}{2\cdot2^{*}}}\\
& \leq C\left[\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}}\right)^{\frac{2\cdot2^{*}-\alpha+4}{2\cdot2^{*}}}\right.\nonumber \\
& \qquad\qquad \left.+\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}}\right)^{\frac{2\cdot2^{*}-\beta+4}{2\cdot2^{*}}}\right].
\end{align*}
\begin{align*}
&\quad \left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\alpha}|v_{n}|^{2r})
+(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{\beta}|v_{n}|^{2r}\right)\\
&\quad\leq \left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{\alpha-4}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}}\right)^{\frac{2\cdot2^{*}-\alpha+4}{2\cdot2^{*}}}\\
& \quad+\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{\beta-4}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}}\right)^{\frac{2\cdot2^{*}-\beta+4}{2\cdot2^{*}}}\\
& \leq C\left[\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}}\right)^{\frac{2\cdot2^{*}-\alpha+4}{2\cdot2^{*}}}\right.\nonumber \\
& \qquad\qquad \left.+\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}}\right)^{\frac{2\cdot2^{*}-\beta+4}{2\cdot2^{*}}}\right].
\end{align*}We get from these inequalities that:
 \begin{equation}
\begin{aligned}
\left(\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}|v_{n}|^{r}\right|^{2^{*}}\right)^{\frac{2}{2^{*}}}
\leq& C(r+2)^{2}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}}\right)^{\frac{2\cdot2^{*}-\alpha+4}{2\cdot2^{*}}}\\
&+C(r+2)^{2}\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}}\right)^{\frac{2\cdot2^{*}-\beta+4}{2\cdot2^{*}}}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\left(\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}|v_{n}|^{r}\right|^{2^{*}}\right)^{\frac{2}{2^{*}}}
\leq& C(r+2)^{2}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}}\right)^{\frac{2\cdot2^{*}-\alpha+4}{2\cdot2^{*}}}\\
&+C(r+2)^{2}\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}}\right)^{\frac{2\cdot2^{*}-\beta+4}{2\cdot2^{*}}}.
\end{aligned}
\end{equation}Let
 \begin{equation*}r_{0}:(r_{0}+2)s=2\cdot2^{*},\ \ \ (r_{0}+2)t \lt 2\cdot2^{*}\ \ \ {\rm and}\ \ \ d=\frac{2^{*}}{s} \gt 1,\end{equation*}
\begin{equation*}r_{0}:(r_{0}+2)s=2\cdot2^{*},\ \ \ (r_{0}+2)t \lt 2\cdot2^{*}\ \ \ {\rm and}\ \ \ d=\frac{2^{*}}{s} \gt 1,\end{equation*} where  $s=\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}$ and
$s=\frac{4\cdot2^{*}}{2\cdot2^{*}-\beta+4}$ and  $t=\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}$. Taking
$t=\frac{4\cdot2^{*}}{2\cdot2^{*}-\alpha+4}$. Taking ![]() $r=r_{0}$ in (6.2) and also letting
$r=r_{0}$ in (6.2) and also letting ![]() $T\rightarrow+\infty$, we have:
$T\rightarrow+\infty$, we have:
 \begin{equation*}|u_{\mu_{n}}|_{(2+r_{0})sd}
\leq (C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})s}
+(C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})t}.\end{equation*}
\begin{equation*}|u_{\mu_{n}}|_{(2+r_{0})sd}
\leq (C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})s}
+(C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})t}.\end{equation*} Set ![]() $2+r_{i+1}=(2+r_{i})d$ for
$2+r_{i+1}=(2+r_{i})d$ for ![]() $i\in\mathbb{N}$. Then
$i\in\mathbb{N}$. Then
 \begin{equation}
\begin{aligned}|u_{\mu_{n}}|_{(2+r_{0})sd^{i+1}}
&\leq \prod\limits_{k=0}^{i}(C(2+r_{k}))^{\frac{1}{2+r_{k}}}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}\right)\\
&\leq C_{\infty}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}\right),
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}|u_{\mu_{n}}|_{(2+r_{0})sd^{i+1}}
&\leq \prod\limits_{k=0}^{i}(C(2+r_{k}))^{\frac{1}{2+r_{k}}}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}\right)\\
&\leq C_{\infty}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}\right),
\end{aligned}
\end{equation} where ![]() $C_{\infty}$ is a positive constant. Let
$C_{\infty}$ is a positive constant. Let ![]() $i\rightarrow\infty$, then there exists a constant C > 0 such that
$i\rightarrow\infty$, then there exists a constant C > 0 such that ![]() $\|u_{\mu_{n}}\|_{\infty}\leq C$ and
$\|u_{\mu_{n}}\|_{\infty}\leq C$ and ![]() $\|u\|_{\infty}\leq C$.
$\|u\|_{\infty}\leq C$.
For the case of (b), ![]() $f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2), then
$f(u)=\tau |u|^{q-2}u+|u|^{p-2}u, \ \tau \gt 0$ satisfies (H1) and (H2), then
 \begin{equation*}\begin{aligned}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\phi &=\tau\int_{\mathbb{R}^{N}}\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{q}|v_{n}|^{2r}
+\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{p}|v_{n}|^{2r}.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\phi &=\tau\int_{\mathbb{R}^{N}}\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{q}|v_{n}|^{2r}
+\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{p}|v_{n}|^{2r}.
\end{aligned}
\end{equation*}On the other hand, by the interpolation inequality, we have,
 \begin{equation*}\begin{aligned}
&\tau\int_{\mathbb{R}^{N}}\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{q}|v_{n}|^{2r}
+\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{p}|v_{n}|^{2r}\\
\leq& \tau\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{q-2}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}}\right)^{\frac{2\cdot2^{*}-q+2}{2\cdot2^{*}}}\\
&+\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{p-4}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}}\right)^{\frac{2\cdot2^{*}-p+4}{2\cdot2^{*}}}\\
\leq& C\left[\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}}\right)^{\frac{2\cdot2^{*}-q+2}{2\cdot2^{*}}}
+\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}}\right)^{\frac{2\cdot2^{*}-p+4}{2\cdot2^{*}}}\right].
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
&\tau\int_{\mathbb{R}^{N}}\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{q}|v_{n}|^{2r}
+\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{p}|v_{n}|^{2r}\\
\leq& \tau\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{q-2}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}}\right)^{\frac{2\cdot2^{*}-q+2}{2\cdot2^{*}}}\\
&+\left(\int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2\cdot2^{*}}\right)^{\frac{p-4}{2\cdot2^{*}}}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}}\right)^{\frac{2\cdot2^{*}-p+4}{2\cdot2^{*}}}\\
\leq& C\left[\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}}\right)^{\frac{2\cdot2^{*}-q+2}{2\cdot2^{*}}}
+\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}}\right)^{\frac{2\cdot2^{*}-p+4}{2\cdot2^{*}}}\right].
\end{aligned}
\end{equation*}From these inequalities, we have:
 \begin{equation}
\begin{aligned}
\left(\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}|v_{n}|^{r}\right|^{2^{*}}\right)^{\frac{2}{2^{*}}}
\leq& C(r+2)^{2}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}}\right)^{\frac{2\cdot2^{*}-q+2}{2\cdot2^{*}}}\\
&+C(r+2)^{2}\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}}\right)^{\frac{2\cdot2^{*}-p+4}{2\cdot2^{*}}}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\left(\int_{\mathbb{R}^{N}}\left|u_{\mu_{n}}^{2}|v_{n}|^{r}\right|^{2^{*}}\right)^{\frac{2}{2^{*}}}
\leq& C(r+2)^{2}
\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}}\right)^{\frac{2\cdot2^{*}-q+2}{2\cdot2^{*}}}\\
&+C(r+2)^{2}\left(\int_{\mathbb{R}^{N}}\left(|v_{n}|^{r}|u_{\mu_{n}}|^{2}\right)^{\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}}\right)^{\frac{2\cdot2^{*}-p+4}{2\cdot2^{*}}}.
\end{aligned}
\end{equation}Let
 \begin{equation*}r_{0}:(r_{0}+2)s=2\cdot2^{*},\ \ \ {\rm and}\ \ \ d=\frac{2^{*}}{s} \gt 1,\end{equation*}
\begin{equation*}r_{0}:(r_{0}+2)s=2\cdot2^{*},\ \ \ {\rm and}\ \ \ d=\frac{2^{*}}{s} \gt 1,\end{equation*} where  $s=\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}$ and
$s=\frac{4\cdot2^{*}}{2\cdot2^{*}-p+4}$ and  $t=\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}$. Then
$t=\frac{2\cdot2^{*}}{2\cdot2^{*}-q+2}$. Then ![]() $(r_{0}+2)t \lt 2\cdot2^{*}$. Assume that
$(r_{0}+2)t \lt 2\cdot2^{*}$. Assume that ![]() $r=r_{0}$ in (6.4), and also taking
$r=r_{0}$ in (6.4), and also taking ![]() $T\rightarrow+\infty$, we get,
$T\rightarrow+\infty$, we get,
 \begin{equation*}|u_{\mu_{n}}|_{(2+r_{0})sd}
\leq (C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})s}
+(C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})t}^{\frac{1}{2}}.\end{equation*}
\begin{equation*}|u_{\mu_{n}}|_{(2+r_{0})sd}
\leq (C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})s}
+(C(2+r_{0}))^{\frac{1}{2+r_{0}}}|u_{\mu_{n}}|_{(2+r_{0})t}^{\frac{1}{2}}.\end{equation*} Set ![]() $2+r_{i+1}=(2+r_{i})d$ for
$2+r_{i+1}=(2+r_{i})d$ for ![]() $i\in\mathbb{N}$. Then
$i\in\mathbb{N}$. Then
 \begin{equation}
\begin{aligned}|u_{\mu_{n}}|_{(2+r_{0})sd^{i+1}}
&\leq \prod\limits_{k=0}^{i}(C(2+r_{k}))^{\frac{1}{2+r_{k}}}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}^{\frac{1}{2}}\right)\\
&\leq C_{\infty}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}^{\frac{1}{2}}\right),
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}|u_{\mu_{n}}|_{(2+r_{0})sd^{i+1}}
&\leq \prod\limits_{k=0}^{i}(C(2+r_{k}))^{\frac{1}{2+r_{k}}}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}^{\frac{1}{2}}\right)\\
&\leq C_{\infty}\left(|u_{\mu_{n}}|_{(2+r_{0})s}
+|u_{\mu_{n}}|_{(2+r_{0})t}^{\frac{1}{2}}\right),
\end{aligned}
\end{equation} where ![]() $C_{\infty}$ is a positive constant. Let
$C_{\infty}$ is a positive constant. Let ![]() $i\rightarrow\infty$, we get that there exists a constant C > 0 such that
$i\rightarrow\infty$, we get that there exists a constant C > 0 such that ![]() $\|u_{\mu_{n}}\|_{\infty}\leq C$ and
$\|u_{\mu_{n}}\|_{\infty}\leq C$ and ![]() $\|u\|_{\infty}\leq C$.
$\|u\|_{\infty}\leq C$.
Step 2. We prove that ![]() $I_{\mu}'(u)+\lambda u=0$.
$I_{\mu}'(u)+\lambda u=0$.
We take ![]() $\phi=\psi e^{-u_{\mu_{n}}}$ with
$\phi=\psi e^{-u_{\mu_{n}}}$ with ![]() $\psi\in C_{0}^{\infty}(\mathbb{R}^{N})$,
$\psi\in C_{0}^{\infty}(\mathbb{R}^{N})$, ![]() $\psi\geq0$, then
$\psi\geq0$, then
 \begin{align*}
0=&\left(I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}\right)[\phi]\\
=&\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}
\left(\nabla\psi e^{-u_{\mu_{n}}}-\psi e^{-u_{\mu_{n}}}\nabla u_{\mu_{n}}\right)\\
& \qquad +\int_{\mathbb{R}^{N}}\nabla u_{\mu_{n}}\left(\nabla\psi e^{-u_{\mu_{n}}}-\psi e^{-u_{\mu_{n}}}\nabla u_{\mu_{n}}\right)\\
&+2\int_{\mathbb{R}^{N}}\left(u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}|\nabla u_{\mu_{n}}|^{2}
+|u_{\mu_{n}}|^{2}\nabla u_{\mu_{n}}\left(\nabla\psi e^{-u_{\mu_{n}}}-\psi e^{-u_{\mu_{n}}}\nabla u_{\mu_{n}}\right)\right)\\
&+\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}
-\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\psi e^{-u_{\mu_{n}}}\\
\leq& \mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}
+\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}\right)\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}\\
&-\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}-2u_{\mu_{n}}\right)\psi e^{-u_{\mu_{n}}}|\nabla u_{\mu_{n}}|^{2}
+\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}\\
& \qquad -\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\psi e^{-u_{\mu_{n}}}.
\end{align*}
\begin{align*}
0=&\left(I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}\right)[\phi]\\
=&\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}
\left(\nabla\psi e^{-u_{\mu_{n}}}-\psi e^{-u_{\mu_{n}}}\nabla u_{\mu_{n}}\right)\\
& \qquad +\int_{\mathbb{R}^{N}}\nabla u_{\mu_{n}}\left(\nabla\psi e^{-u_{\mu_{n}}}-\psi e^{-u_{\mu_{n}}}\nabla u_{\mu_{n}}\right)\\
&+2\int_{\mathbb{R}^{N}}\left(u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}|\nabla u_{\mu_{n}}|^{2}
+|u_{\mu_{n}}|^{2}\nabla u_{\mu_{n}}\left(\nabla\psi e^{-u_{\mu_{n}}}-\psi e^{-u_{\mu_{n}}}\nabla u_{\mu_{n}}\right)\right)\\
&+\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}
-\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\psi e^{-u_{\mu_{n}}}\\
\leq& \mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}
+\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}\right)\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}\\
&-\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}-2u_{\mu_{n}}\right)\psi e^{-u_{\mu_{n}}}|\nabla u_{\mu_{n}}|^{2}
+\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}\\
& \qquad -\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\psi e^{-u_{\mu_{n}}}.
\end{align*} Since ![]() $\mu_{n}\rightarrow 0^{+}$ and
$\mu_{n}\rightarrow 0^{+}$ and ![]() $\|u_{\mu_{n}}\|_{\infty}\leq C$, then (6.1) shows that:
$\|u_{\mu_{n}}\|_{\infty}\leq C$, then (6.1) shows that:
 \begin{equation*}\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}\rightarrow 0.\end{equation*}
\begin{equation*}\mu_{n}\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta-2}\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}\rightarrow 0.\end{equation*} By the weak convergence of ![]() $u_{\mu_{n}}$, the Lebesgue’s dominated convergence theorem and the Hölder inequality, we see that:
$u_{\mu_{n}}$, the Lebesgue’s dominated convergence theorem and the Hölder inequality, we see that:
 \begin{equation*}\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}\right)\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}\rightarrow
\int_{\mathbb{R}^{N}}\left(1+2u^{2}\right)\nabla u\nabla\psi e^{-u},\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}\right)\nabla u_{\mu_{n}}\nabla\psi e^{-u_{\mu_{n}}}\rightarrow
\int_{\mathbb{R}^{N}}\left(1+2u^{2}\right)\nabla u\nabla\psi e^{-u},\end{equation*} \begin{equation*}\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}\rightarrow
\lambda\int_{\mathbb{R}^{N}}u\psi e^{-u},\end{equation*}
\begin{equation*}\lambda_{\mu_{n}}\int_{\mathbb{R}^{N}}u_{\mu_{n}}\psi e^{-u_{\mu_{n}}}\rightarrow
\lambda\int_{\mathbb{R}^{N}}u\psi e^{-u},\end{equation*}and
 \begin{equation*}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\psi e^{-u_{\mu_{n}}}\rightarrow
\int_{\mathbb{R}^{N}}f(u)\psi e^{-u}.\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{N}}f(u_{\mu_{n}})\psi e^{-u_{\mu_{n}}}\rightarrow
\int_{\mathbb{R}^{N}}f(u)\psi e^{-u}.\end{equation*}Furthermore, we deduce from the Fatou’s lemma that:
 \begin{equation*}\liminf\limits_{n\rightarrow\infty}\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}-2u_{\mu_{n}}\right)\psi e^{-u_{\mu_{n}}}|\nabla u_{\mu_{n}}|^{2}
\geq\int_{\mathbb{R}^{N}}\left(1+2u^{2}-2u\right)\psi e^{-u}|\nabla u|^{2}.\end{equation*}
\begin{equation*}\liminf\limits_{n\rightarrow\infty}\int_{\mathbb{R}^{N}}\left(1+2u_{\mu_{n}}^{2}-2u_{\mu_{n}}\right)\psi e^{-u_{\mu_{n}}}|\nabla u_{\mu_{n}}|^{2}
\geq\int_{\mathbb{R}^{N}}\left(1+2u^{2}-2u\right)\psi e^{-u}|\nabla u|^{2}.\end{equation*}From these convergence, we get:
 \begin{equation}
\begin{aligned}
0\leq&\int_{\mathbb{R}^{N}}\nabla u\left(\nabla\psi e^{-u}-\psi e^{-u}\nabla u\right)
+2\int_{\mathbb{R}^{N}}|u|^{2}\nabla u\left(\nabla\psi e^{-u}-\psi e^{-u}\nabla u\right)\\
&+2\int_{\mathbb{R}^{N}}u\psi e^{-u}|\nabla u|^{2}+\lambda\int_{\mathbb{R}^{N}}u\psi e^{-u}
-\int_{\mathbb{R}^{N}}f(u)\psi e^{-u}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
0\leq&\int_{\mathbb{R}^{N}}\nabla u\left(\nabla\psi e^{-u}-\psi e^{-u}\nabla u\right)
+2\int_{\mathbb{R}^{N}}|u|^{2}\nabla u\left(\nabla\psi e^{-u}-\psi e^{-u}\nabla u\right)\\
&+2\int_{\mathbb{R}^{N}}u\psi e^{-u}|\nabla u|^{2}+\lambda\int_{\mathbb{R}^{N}}u\psi e^{-u}
-\int_{\mathbb{R}^{N}}f(u)\psi e^{-u}.
\end{aligned}
\end{equation} For any ![]() $\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$ with
$\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$ with ![]() $\varphi\geq0$. We take a sequence
$\varphi\geq0$. We take a sequence ![]() $\{\psi_{n}\}$ with the property that
$\{\psi_{n}\}$ with the property that ![]() $\psi_{n}\in C_{0}^{\infty}(\mathbb{R}^{N})$ is nonnegative for every
$\psi_{n}\in C_{0}^{\infty}(\mathbb{R}^{N})$ is nonnegative for every ![]() $n\in\mathbb{N}$ such that:
$n\in\mathbb{N}$ such that:
and ![]() $\{\psi_{n}\}$ is bounded in
$\{\psi_{n}\}$ is bounded in ![]() $L^{\infty}(\mathbb{R}^{N})$. Then we deduce from (6.6) that:
$L^{\infty}(\mathbb{R}^{N})$. Then we deduce from (6.6) that:
 \begin{equation}
\begin{aligned}
0\leq&\int_{\mathbb{R}^{N}}\nabla u\nabla\varphi
+2\int_{\mathbb{R}^{N}}\left(|u|^{2}\nabla u\nabla\varphi+u\varphi|\nabla u|^{2}\right)+\lambda\int_{\mathbb{R}^{N}}u\varphi
-\int_{\mathbb{R}^{N}}f(u)\varphi.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
0\leq&\int_{\mathbb{R}^{N}}\nabla u\nabla\varphi
+2\int_{\mathbb{R}^{N}}\left(|u|^{2}\nabla u\nabla\varphi+u\varphi|\nabla u|^{2}\right)+\lambda\int_{\mathbb{R}^{N}}u\varphi
-\int_{\mathbb{R}^{N}}f(u)\varphi.
\end{aligned}
\end{equation} In the same way as before, take ![]() $\phi=\psi e^{u_{\mu_{n}}}$, we have a different inequality. Also, since
$\phi=\psi e^{u_{\mu_{n}}}$, we have a different inequality. Also, since ![]() $\varphi=\varphi^{+}-\varphi^{-}$ for any
$\varphi=\varphi^{+}-\varphi^{-}$ for any ![]() $\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$, then
$\varphi\in C_{0}^{\infty}(\mathbb{R}^{N})$, then ![]() $I_{\mu}'(u)+\lambda u=0$.
$I_{\mu}'(u)+\lambda u=0$.
Step 3. Conclusion.
We deduce form ![]() $I_{\mu}'(u)+\lambda u=0$ that
$I_{\mu}'(u)+\lambda u=0$ that ![]() $Q(u):=Q_{0}(u)=0$. It shows that:
$Q(u):=Q_{0}(u)=0$. It shows that:
 \begin{equation*}Q_{\mu}(u_{\mu_{n}})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{\mu_{n}})u_{\mu_{n}}-2F(u_{\mu_{n}})]\rightarrow
Q_{\mu}(u)+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)].\end{equation*}
\begin{equation*}Q_{\mu}(u_{\mu_{n}})+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u_{\mu_{n}})u_{\mu_{n}}-2F(u_{\mu_{n}})]\rightarrow
Q_{\mu}(u)+\frac{N}{2}\int_{\mathbb{R}^{N}}[f(u)u-2F(u)].\end{equation*}Then by the weak lower semicontinuity, there holds:
 \begin{equation}
\mu\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta}\rightarrow0,\ \ \ \int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|\nabla u|^{2},\ \ \ \int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2}|\nabla u_{\mu_{n}}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2},
\end{equation}
\begin{equation}
\mu\int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{\theta}\rightarrow0,\ \ \ \int_{\mathbb{R}^{N}}|\nabla u_{\mu_{n}}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|\nabla u|^{2},\ \ \ \int_{\mathbb{R}^{N}}|u_{\mu_{n}}|^{2}|\nabla u_{\mu_{n}}|^{2}\rightarrow\int_{\mathbb{R}^{N}}|u|^{2}|\nabla u|^{2},
\end{equation} which implies that  $I(u)=\lim\limits_{n\rightarrow\infty}I_{\mu}(u_{\mu_{n}})=c$. Furthermore, we get from (6.8) that
$I(u)=\lim\limits_{n\rightarrow\infty}I_{\mu}(u_{\mu_{n}})=c$. Furthermore, we get from (6.8) that
 \begin{equation}
I_{\mu}'(u_{n})[u_{n}]\rightarrow I_{\mu}'(u_{\mu})[u_{\mu}].
\end{equation}
\begin{equation}
I_{\mu}'(u_{n})[u_{n}]\rightarrow I_{\mu}'(u_{\mu})[u_{\mu}].
\end{equation} Thus, we combine (6.8) with (6.9), there must be ![]() $\lambda_{n}|u_{\mu_{n}}|_{2}^{2}\rightarrow\lambda_{\mu}|u|_{2}^{2}$. So the condition
$\lambda_{n}|u_{\mu_{n}}|_{2}^{2}\rightarrow\lambda_{\mu}|u|_{2}^{2}$. So the condition ![]() $\lambda_{\mu}\neq0$ shows that
$\lambda_{\mu}\neq0$ shows that  $|u|_{2}^{2}=\lim\limits_{n\rightarrow\infty}a_{n}$.
$|u|_{2}^{2}=\lim\limits_{n\rightarrow\infty}a_{n}$.
Now, we give the proofs of Theorems 1.1 and 1.2.
Proof of Theorem 1.1
For the case of ![]() $N\geq2$: we define,
$N\geq2$: we define,
 \begin{equation*}d^{*}(a):=\lim\limits_{\mu\rightarrow0^{+}}m_{\mu}(a)\in(0,+\infty).\end{equation*}
\begin{equation*}d^{*}(a):=\lim\limits_{\mu\rightarrow0^{+}}m_{\mu}(a)\in(0,+\infty).\end{equation*} From ![]() $\S$ 4 we can obtain
$\S$ 4 we can obtain ![]() $\mu_{n}\rightarrow 0^{+}$,
$\mu_{n}\rightarrow 0^{+}$, ![]() $I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$,
$I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$, ![]() $I_{\mu_{n}}(u_{\mu_{n}})\rightarrow d^{*}(a)\neq0$ for
$I_{\mu_{n}}(u_{\mu_{n}})\rightarrow d^{*}(a)\neq0$ for ![]() $u_{\mu_{n}}\in S_{r}(a_{n})$ with
$u_{\mu_{n}}\in S_{r}(a_{n})$ with ![]() $0 \lt a_{n}\leq a$ and
$0 \lt a_{n}\leq a$ and ![]() $u_{\mu_{n}}\geq0$. Then, we deduce from Lemma 2.2 that
$u_{\mu_{n}}\geq0$. Then, we deduce from Lemma 2.2 that ![]() $\lambda_{\mu_{n}} \gt 0$. Now by Lemma 6.1 there exists
$\lambda_{\mu_{n}} \gt 0$. Now by Lemma 6.1 there exists ![]() $\lambda_{0}\in\mathbb{R}$ and
$\lambda_{0}\in\mathbb{R}$ and  $v\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that
$v\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that ![]() $v\not\equiv0$ and
$v\not\equiv0$ and ![]() $v\geq0$ such that:
$v\geq0$ such that:
Hence by Lemma 2.2 there holds ![]() $\lambda_{0} \gt 0$. Since
$\lambda_{0} \gt 0$. Since ![]() $\lambda_{\mu_{n}}\rightarrow\lambda_{0}$, we have
$\lambda_{\mu_{n}}\rightarrow\lambda_{0}$, we have ![]() $\lambda_{\mu_{n}}\neq0$ for n large. Then
$\lambda_{\mu_{n}}\neq0$ for n large. Then ![]() $a_{n}=a$ for n large and
$a_{n}=a$ for n large and ![]() $|v|_{2}=a$. It follows that v is a non-trivial non-negative normalized solution to (1.1). To study the ground state normalized solution, we define:
$|v|_{2}=a$. It follows that v is a non-trivial non-negative normalized solution to (1.1). To study the ground state normalized solution, we define:
 \begin{equation*}d(a):=\inf\left\{I(v): v\in\widetilde{S}(a),I|_{\widetilde{S}(a)}(v)=0,v\neq0\right\}.\end{equation*}
\begin{equation*}d(a):=\inf\left\{I(v): v\in\widetilde{S}(a),I|_{\widetilde{S}(a)}(v)=0,v\neq0\right\}.\end{equation*} Then ![]() $d(a)\leq I(v)=d^{*}(a)$. Moreover, we conclude that
$d(a)\leq I(v)=d^{*}(a)$. Moreover, we conclude that ![]() $d(a) \gt 0$, see Lemma 4.2 for details. We choose a sequence
$d(a) \gt 0$, see Lemma 4.2 for details. We choose a sequence  $v_{n}\in\widetilde{S}(a)$,
$v_{n}\in\widetilde{S}(a)$,  $I|_{\widetilde{S}(a)}(v_{n})=0$,
$I|_{\widetilde{S}(a)}(v_{n})=0$, ![]() $v_{n}\neq0$ and
$v_{n}\neq0$ and ![]() $v_{n}\geq0$, such that
$v_{n}\geq0$, such that ![]() $I(v_{n})\rightarrow d(a)$. By Lemma 6.1, up to a subsequence, there exists
$I(v_{n})\rightarrow d(a)$. By Lemma 6.1, up to a subsequence, there exists ![]() $\lambda\in\mathbb{R}$ and
$\lambda\in\mathbb{R}$ and  $u\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that u ≠ 0 and
$u\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that u ≠ 0 and ![]() $u\geq0$ such that:
$u\geq0$ such that:
We again use the Lemma 2.2 that λ ≠ 0, hence ![]() $|u|_{2}=a$. It follows that u is a minimizer of d(a). Finally, u is classical and strictly positive since
$|u|_{2}=a$. It follows that u is a minimizer of d(a). Finally, u is classical and strictly positive since ![]() $u\in L^{\infty}(\mathbb{R}^{N})$, see Lemma 2.6 in [Reference Liu, Liu and Wang28].
$u\in L^{\infty}(\mathbb{R}^{N})$, see Lemma 2.6 in [Reference Liu, Liu and Wang28].
Proof of Theorem 1.2 i)
For the case of ![]() $N\geq2$: we define,
$N\geq2$: we define,
 \begin{equation*}d_{\tau}^{*}(a):=\lim\limits_{\mu\rightarrow0^{+}}m_{\mu}(a,\tau)\in(-\infty,0).\end{equation*}
\begin{equation*}d_{\tau}^{*}(a):=\lim\limits_{\mu\rightarrow0^{+}}m_{\mu}(a,\tau)\in(-\infty,0).\end{equation*} From ![]() $\S$ 5.2 we can obtain
$\S$ 5.2 we can obtain ![]() $\mu_{n}\rightarrow 0^{+}$,
$\mu_{n}\rightarrow 0^{+}$, ![]() $I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$,
$I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$, ![]() $I_{\mu_{n}}(u_{\mu_{n}})\rightarrow d_{\tau}^{*}(a)\neq0$ for
$I_{\mu_{n}}(u_{\mu_{n}})\rightarrow d_{\tau}^{*}(a)\neq0$ for ![]() $u_{\mu_{n}}\in S_{r}(a_{n})$ with
$u_{\mu_{n}}\in S_{r}(a_{n})$ with ![]() $0 \lt a_{n}\leq a$ and
$0 \lt a_{n}\leq a$ and ![]() $u_{\mu_{n}}\geq0$. Then, we deduce from Lemma 2.2 that
$u_{\mu_{n}}\geq0$. Then, we deduce from Lemma 2.2 that ![]() $\lambda_{\mu_{n}} \gt 0$. Now by Lemma 6.1 there exists
$\lambda_{\mu_{n}} \gt 0$. Now by Lemma 6.1 there exists ![]() $\lambda_{0}\in\mathbb{R}$ and
$\lambda_{0}\in\mathbb{R}$ and  $v\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that v ≠ 0 and
$v\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that v ≠ 0 and ![]() $v\geq0$ such that:
$v\geq0$ such that:
Hence by Lemma 2.2 there holds ![]() $\lambda_{0} \gt 0$. Since
$\lambda_{0} \gt 0$. Since ![]() $\lambda_{\mu_{n}}\rightarrow\lambda_{0}$, we have
$\lambda_{\mu_{n}}\rightarrow\lambda_{0}$, we have ![]() $\lambda_{\mu_{n}}\neq0$ for n large. Then
$\lambda_{\mu_{n}}\neq0$ for n large. Then ![]() $a_{n}=a$ for n large and
$a_{n}=a$ for n large and ![]() $|v|_{2}=a$. It follows that v is a non-trivial non-negative normalized solution to
$|v|_{2}=a$. It follows that v is a non-trivial non-negative normalized solution to ![]() $(\mathcal{K})$. To study the ground state normalized solution, we define:
$(\mathcal{K})$. To study the ground state normalized solution, we define:
 \begin{equation*}d_{\tau}(a):=\inf\left\{I(v): v\in\widetilde{S}(a),I|_{\widetilde{S}(a)}(v)=0,v\neq0\right\}.\end{equation*}
\begin{equation*}d_{\tau}(a):=\inf\left\{I(v): v\in\widetilde{S}(a),I|_{\widetilde{S}(a)}(v)=0,v\neq0\right\}.\end{equation*} Then ![]() $d_{\tau}(a)\leq I(v)=d_{\tau}^{*}(a)$. Furthermore, we have that
$d_{\tau}(a)\leq I(v)=d_{\tau}^{*}(a)$. Furthermore, we have that ![]() $d_{\tau}(a) \lt 0$, see Lemma 5.5. We take a sequence
$d_{\tau}(a) \lt 0$, see Lemma 5.5. We take a sequence  $v_{n}\in\widetilde{S}(a)$,
$v_{n}\in\widetilde{S}(a)$,  $I|_{\widetilde{S}(a)}(v_{n})=0$,
$I|_{\widetilde{S}(a)}(v_{n})=0$, ![]() $v_{n}\neq0$ and
$v_{n}\neq0$ and ![]() $v_{n}\geq0$ such that
$v_{n}\geq0$ such that ![]() $I(v_{n})\rightarrow d_{\tau}(a)$. By Lemma 6.1, up to a subsequence, there exists
$I(v_{n})\rightarrow d_{\tau}(a)$. By Lemma 6.1, up to a subsequence, there exists ![]() $\lambda\in\mathbb{R}$ and
$\lambda\in\mathbb{R}$ and  $\widehat{u}\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that
$\widehat{u}\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that ![]() $\widehat{u}\neq0$ and
$\widehat{u}\neq0$ and ![]() $\widehat{u}\geq0$ such that:
$\widehat{u}\geq0$ such that:
We again use the Lemma 2.2 that λ ≠ 0, hence ![]() $|\widehat{u}|_{2}=a$. It shows that
$|\widehat{u}|_{2}=a$. It shows that ![]() $\widehat{u}$ is a minimizer of
$\widehat{u}$ is a minimizer of ![]() $d_{\tau}(a)$. Finally, by Lemma 2.6 in [Reference Liu, Liu and Wang29],
$d_{\tau}(a)$. Finally, by Lemma 2.6 in [Reference Liu, Liu and Wang29], ![]() $\widehat{u}$ is classical and strictly positive since
$\widehat{u}$ is classical and strictly positive since ![]() $\widehat{u}\in L^{\infty}(\mathbb{R}^{N})$.
$\widehat{u}\in L^{\infty}(\mathbb{R}^{N})$.
Proof of Theorem 1.2 ii)
For the case of ![]() $N\geq2$: we define,
$N\geq2$: we define,
 \begin{equation*}\overline{d_{\tau}^{*}}(a):=\lim\limits_{\mu\rightarrow0^{+}}\sigma_{\mu}(a,\tau)\in(0,+\infty).\end{equation*}
\begin{equation*}\overline{d_{\tau}^{*}}(a):=\lim\limits_{\mu\rightarrow0^{+}}\sigma_{\mu}(a,\tau)\in(0,+\infty).\end{equation*} From ![]() $\S$ 5.3 we obtain
$\S$ 5.3 we obtain ![]() $\mu_{n}\rightarrow 0^{+}$,
$\mu_{n}\rightarrow 0^{+}$, ![]() $I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$,
$I_{\mu_{n}}'(u_{n})+\lambda_{\mu_{n}}u_{\mu_{n}}=0$, ![]() $I_{\mu_{n}}(u_{\mu_{n}})\rightarrow \overline{d_{\tau}^{*}}(a)\neq0$ for
$I_{\mu_{n}}(u_{\mu_{n}})\rightarrow \overline{d_{\tau}^{*}}(a)\neq0$ for ![]() $u_{\mu_{n}}\in S_{r}(a_{n}),$ with
$u_{\mu_{n}}\in S_{r}(a_{n}),$ with ![]() $0 \lt a_{n}\leq a$ and
$0 \lt a_{n}\leq a$ and ![]() $u_{\mu_{n}}\geq0$. Then we deduce from the Lemma 2.2 that
$u_{\mu_{n}}\geq0$. Then we deduce from the Lemma 2.2 that ![]() $\lambda_{\mu_{n}} \gt 0$. Now by Lemma 6.1 there exists
$\lambda_{\mu_{n}} \gt 0$. Now by Lemma 6.1 there exists ![]() $\lambda_{0}\in\mathbb{R}$ and
$\lambda_{0}\in\mathbb{R}$ and  $\overline{u}\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that
$\overline{u}\in W_{rad}^{1,2}(\mathbb{R}^{N})\cap L^{\infty}(\mathbb{R}^{N})$ with the properties that ![]() $\overline{u}\neq0$ and
$\overline{u}\neq0$ and ![]() $v\geq0$ such that:
$v\geq0$ such that:
By Lemma 2.2 there holds ![]() $\lambda_{0} \gt 0$. Since
$\lambda_{0} \gt 0$. Since ![]() $\lambda_{\mu_{n}}\rightarrow\lambda_{0}$, we get that
$\lambda_{\mu_{n}}\rightarrow\lambda_{0}$, we get that ![]() $\lambda_{\mu_{n}}\neq0$ for n large. Then
$\lambda_{\mu_{n}}\neq0$ for n large. Then ![]() $a_{n}=a$ for n large and
$a_{n}=a$ for n large and ![]() $|\overline{u}|_{2}=a$. It follows that
$|\overline{u}|_{2}=a$. It follows that ![]() $\overline{u}$ is a non-trivial non-negative normalized solution of mountain-pass type to (1.1). By using the strong maximum principle, we get
$\overline{u}$ is a non-trivial non-negative normalized solution of mountain-pass type to (1.1). By using the strong maximum principle, we get ![]() $\overline{u}$ is positive. Since
$\overline{u}$ is positive. Since ![]() $\overline{u}\in L^{\infty}(\mathbb{R}^{N})$, then
$\overline{u}\in L^{\infty}(\mathbb{R}^{N})$, then ![]() $\overline{u}$ is classical, see Lemma 2.6 in [Reference Liu, Liu and Wang28].
$\overline{u}$ is classical, see Lemma 2.6 in [Reference Liu, Liu and Wang28].