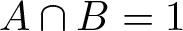1. Introduction
All groups considered here will be finite.
A significant number of articles investigating the properties of groups expressible as a product of two supersoluble subgroups were published since the 1957 paper by Baer [Reference Baer2] in which he proved that a normal product G = AB of two supersoluble subgroups A and B is supersoluble provided that the derived subgroup Gʹ is nilpotent. There has been many generalizations of this theorem. Instead of having normal subgroups, certain permutability conditions were imposed on the factors. The case in which A permutes with every subgroup of B and B permutes with every subgroup of A, that is, when G is a mutually permutable product of A and B, is in fact one of the most interesting cases and has been investigated in detail (see [Reference Ballester-Bolinches, Esteban-Romero and Asaad5] for a thorough review of results in this context and also [Reference Amberg, Franciosi and de Giovanni1] for general results on products).
In this article, we study a weak form of a normal product arising quite frequently in the structural study of mutually permutable products and appears not to have been investigated in detail.
Definition 1.1. Let G = AB be a product of subgroups A and B. We say that G is a weak normal product of A and B if
(a) A is normal in G.
(b) B permutes with all the maximal subgroups of Sylow subgroups of A.
As an important first step in the study of weak normal products G = AB and motivated by the mutually permutable case, we analyse the situation ![]() $A \cap B=1$. In this case, they are semidirect products of A and B.
$A \cap B=1$. In this case, they are semidirect products of A and B.
Definition 1.2. Let the group G = AB be the weak normal product of A and B with A normal in G. We say that G is a weak direct product of A and B if ![]() $A \cap B = 1$. In this case, we write
$A \cap B = 1$. In this case, we write ![]() $G = [A]B$.
$G = [A]B$.
We study these products when the factors are supersoluble and widely supersoluble and analyse the behaviour of the residuals associated to these classes of groups. Recall that a widely supersoluble group, or w-supersoluble group for short, is defined as a group G such that every Sylow subgroup of G is ![]() $\mathbb{P}$-subnormal in G (a subgroup H of a group G is
$\mathbb{P}$-subnormal in G (a subgroup H of a group G is ![]() $\mathbb{P}$-subnormal in G whenever either H = G or there exists a chain of subgroups
$\mathbb{P}$-subnormal in G whenever either H = G or there exists a chain of subgroups ![]() $H=H_{0} \leqslant H_{1} \leqslant \cdots \leqslant H_{n-1} \leqslant H_{n}=G$, such that
$H=H_{0} \leqslant H_{1} \leqslant \cdots \leqslant H_{n-1} \leqslant H_{n}=G$, such that ![]() $| H_{i} {:} H_{i-1}|$ is a prime for every
$| H_{i} {:} H_{i-1}|$ is a prime for every ![]() $i=1, \dots, n$).
$i=1, \dots, n$).
The class of w-supersoluble groups, denoted ![]() $w\mathfrak{U} $, is a subgroup-closed saturated formation containing the subgroup-closed saturated formation
$w\mathfrak{U} $, is a subgroup-closed saturated formation containing the subgroup-closed saturated formation ![]() $\mathfrak{U} $ of all supersoluble groups. Moreover w-supersoluble groups have a Sylow tower of supersoluble type (see [Reference Valisev, Valiseva and Tyutyanov8, Corollary]).
$\mathfrak{U} $ of all supersoluble groups. Moreover w-supersoluble groups have a Sylow tower of supersoluble type (see [Reference Valisev, Valiseva and Tyutyanov8, Corollary]).
Our first aim is to show that the saturated formations of all supersoluble groups and w-supersoluble groups are closed under the formation of weak direct products.
Theorem A.
Let ![]() $ G =[A]B $ be a weak direct product of A and B. If A and B belong to
$ G =[A]B $ be a weak direct product of A and B. If A and B belong to ![]() $ \mathfrak{U} $, then G is also supersoluble.
$ \mathfrak{U} $, then G is also supersoluble.
Theorem A will be very useful in the proofs of Theorem B and Theorem C. Also we obtain the following result as a corollary.
Corollary A.
Let ![]() $ G =[A]B $ be a weak direct product of A and B. If A and B belong to
$ G =[A]B $ be a weak direct product of A and B. If A and B belong to ![]() $ w\mathfrak{U} $, then G is w-supersoluble.
$ w\mathfrak{U} $, then G is w-supersoluble.
Our second aim is to show that the product of the supersoluble (respectively, w-supersoluble) residuals of the factors of weak direct products is just the supersoluble (respectively, w-supersoluble) residual of the group.
Theorem B.
Suppose that ![]() $ \mathfrak{F} =\mathfrak{U}$ or
$ \mathfrak{F} =\mathfrak{U}$ or ![]() $ \mathfrak{F} =w\mathfrak{U}$. Let
$ \mathfrak{F} =w\mathfrak{U}$. Let ![]() $ G =[A]B $ be a weak direct product of A and B. Then
$ G =[A]B $ be a weak direct product of A and B. Then
We now analyse the behaviour of weak normal products with respect to the formations of all supersoluble and w-supersoluble groups. Our next result shows that Baer’s theorem can be generalized in this new direction:
Theorem C.
Let G = AB be a weak normal product of A and B. If Gʹ is nilpotent, A is normal in G and ![]() $ A, B\in \mathfrak{U} $, then
$ A, B\in \mathfrak{U} $, then ![]() $ G \in \mathfrak{U}$.
$ G \in \mathfrak{U}$.
As a corollary, we obtain the result for ![]() $w \mathfrak{U} $-groups.
$w \mathfrak{U} $-groups.
Corollary B.
Let the group G = AB be a weak normal product of ![]() $ w\mathfrak{U} $-subgroups A and B. If Gʹ is nilpotent and A is normal in G, then G belongs to
$ w\mathfrak{U} $-subgroups A and B. If Gʹ is nilpotent and A is normal in G, then G belongs to ![]() $w \mathfrak{U} $.
$w \mathfrak{U} $.
Our second objective is to investigate the residuals of weak normal products. Unfortunately, it does not follow that ![]() $ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}} $ when G is a weak normal product as the following examples show. Example 1.3(ii) generalizing (i) was communicated to the authors by the referee:
$ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}} $ when G is a weak normal product as the following examples show. Example 1.3(ii) generalizing (i) was communicated to the authors by the referee:
(i) Let
 \begin{align*}A=\langle g_2,g_4,g_5,g_6,g_7\mid \mbox{}&g_2^3=g_4^3=g_5^3=g_6^3=g_7^3=1,\\
&g_4^{g_2}=g_4g_6, g_5^{g_2}=g_5g_7, g_6^{g_2}=g_6, g_7^{g_2}=g_7,\\
&g_5^{g_4}=g_5, g_6^{g_4}=g_6, g_7^{g_4}=g_7,\\
&g_6^{g_5}=g_6, g_7^{g_5}=g_7,\\
&g_7^{g_6}=g_7\rangle.
\end{align*}
\begin{align*}A=\langle g_2,g_4,g_5,g_6,g_7\mid \mbox{}&g_2^3=g_4^3=g_5^3=g_6^3=g_7^3=1,\\
&g_4^{g_2}=g_4g_6, g_5^{g_2}=g_5g_7, g_6^{g_2}=g_6, g_7^{g_2}=g_7,\\
&g_5^{g_4}=g_5, g_6^{g_4}=g_6, g_7^{g_4}=g_7,\\
&g_6^{g_5}=g_6, g_7^{g_5}=g_7,\\
&g_7^{g_6}=g_7\rangle.
\end{align*}Let
 $Q=\langle b\rangle\cong C_4$ act on A via
$Q=\langle b\rangle\cong C_4$ act on A via
 \begin{align*}
g_2^b&=g_2,&g_4^{b}&=g_4g_5,&g_5^b&=g_4g_5^2,&g_6^{b}&=g_6g_7,&g_7^{b}&=g_6g_7^2.
\end{align*}
\begin{align*}
g_2^b&=g_2,&g_4^{b}&=g_4g_5,&g_5^b&=g_4g_5^2,&g_6^{b}&=g_6g_7,&g_7^{b}&=g_6g_7^2.
\end{align*}Let
 $G=[A]Q$ be the corresponding semidirect product.
$G=[A]Q$ be the corresponding semidirect product.Note that
 $A^\prime=\Phi(A)=\langle g_6, g_7\rangle$. Let
$A^\prime=\Phi(A)=\langle g_6, g_7\rangle$. Let  $A_0=\langle g_4, g_5\rangle$. Then A 0 is not a normal subgroup of A but is normalized by Q. Let
$A_0=\langle g_4, g_5\rangle$. Then A 0 is not a normal subgroup of A but is normalized by Q. Let  $B=A_0\langle b\rangle$, then
$B=A_0\langle b\rangle$, then  ${\rm Core}_G(B)=1$. Furthermore, B permutes with the 13 maximal subgroups of A. The supersoluble residual of G is
${\rm Core}_G(B)=1$. Furthermore, B permutes with the 13 maximal subgroups of A. The supersoluble residual of G is  $\langle g_4, g_5, g_6,g_7\rangle$, giving a quotient isomorphic to C 12. Consequently,
$\langle g_4, g_5, g_6,g_7\rangle$, giving a quotient isomorphic to C 12. Consequently,  $ G^{\mathfrak{U}}\neq A^{\mathfrak{U}}B^{\mathfrak{U}} $. This group corresponds to SmallGroup(972, 406) of GAP.
$ G^{\mathfrak{U}}\neq A^{\mathfrak{U}}B^{\mathfrak{U}} $. This group corresponds to SmallGroup(972, 406) of GAP.(ii) Suppose p is a prime number and n is a positive integer, where n is not a multiple of p, and the order of p modulo n is 2. Let
 ${\bf{F}}_{p^2}$ be the Galois field of order p 2, and note that n is a factor of
${\bf{F}}_{p^2}$ be the Galois field of order p 2, and note that n is a factor of  ${p^2}-1$, so there is an element β of multiplicative order n in
${p^2}-1$, so there is an element β of multiplicative order n in  ${\bf{F}}_{p^2}$. Let
${\bf{F}}_{p^2}$. Let  $V=U_{0} \oplus U_{1}$ be a vector space of dimension 2 over
$V=U_{0} \oplus U_{1}$ be a vector space of dimension 2 over  ${\bf{F}}_{p^2}$, where U 0 and U 1 are one-dimensional
${\bf{F}}_{p^2}$, where U 0 and U 1 are one-dimensional  ${\bf{F}}_{p^2}$-subspaces of V. Take elements a and b in the general linear group
${\bf{F}}_{p^2}$-subspaces of V. Take elements a and b in the general linear group  ${\rm GL}_{2}(p^2)$, with
${\rm GL}_{2}(p^2)$, with
 \begin{equation*}a=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \qquad b=\begin{bmatrix} \beta & 0\\ 0 & \beta \end{bmatrix}.\end{equation*}
\begin{equation*}a=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \qquad b=\begin{bmatrix} \beta & 0\\ 0 & \beta \end{bmatrix}.\end{equation*}Then V can be regarded as an
 ${\bf{F}}_{p^2} \langle a, b \rangle$-module. Let
${\bf{F}}_{p^2} \langle a, b \rangle$-module. Let  $G=[V] \langle a, b \rangle$ be the corresponding semidirect product. Consider the following subgroups of G:
$G=[V] \langle a, b \rangle$ be the corresponding semidirect product. Consider the following subgroups of G:
 \begin{equation*} P=\langle a \rangle \simeq \textbf{C}_{p}, \quad A=VP, \quad Q=\langle b \rangle \simeq \textbf{C}_{n}, \quad B=U_{0}Q.\end{equation*}
\begin{equation*} P=\langle a \rangle \simeq \textbf{C}_{p}, \quad A=VP, \quad Q=\langle b \rangle \simeq \textbf{C}_{n}, \quad B=U_{0}Q.\end{equation*}As in (i), A is normal in AB = G,
 $A^\prime=\Phi(A)=[V,P]=U_{1}$, U 0 is an
$A^\prime=\Phi(A)=[V,P]=U_{1}$, U 0 is an  ${\bf{F}}_{p}Q$-simple module,
${\bf{F}}_{p}Q$-simple module,  $B^\prime=[U_{0},Q]=U_{0}$, the core of B in G is 1, the number of maximal subgroups of A is
$B^\prime=[U_{0},Q]=U_{0}$, the core of B in G is 1, the number of maximal subgroups of A is  $(p^{3}-1)/(p-1)=p^{2}+p+1$, A is the unique Sylow p-subgroup of G and all the maximal subgroups of A permute with B, while the supersoluble residual of G is
$(p^{3}-1)/(p-1)=p^{2}+p+1$, A is the unique Sylow p-subgroup of G and all the maximal subgroups of A permute with B, while the supersoluble residual of G is  $G^{\mathfrak U}=V$, with
$G^{\mathfrak U}=V$, with  $G/G^{\mathfrak U} \simeq PQ \simeq \textbf{C}_{pn}$ and
$G/G^{\mathfrak U} \simeq PQ \simeq \textbf{C}_{pn}$ and  $G^{\mathfrak U} \neq A^{\mathfrak U}B^{\mathfrak U}$. This construction can be carried out when p = 2 and n = 3, giving an Example with
$G^{\mathfrak U} \neq A^{\mathfrak U}B^{\mathfrak U}$. This construction can be carried out when p = 2 and n = 3, giving an Example with  $|G|=2^{5}3=96$; moreover, there is a maximal subgroup of A which does not permute with the Sylow subgroup Q of B.
$|G|=2^{5}3=96$; moreover, there is a maximal subgroup of A which does not permute with the Sylow subgroup Q of B.
We will use Theorem C to prove the following result (note that Example 1.3(ii) suggests the permutability hypothesis in Theorem D and Corollary D):
Theorem D.
Let the group G = AB be a product of the subgroups A and B. Assume that A is a normal subgroup of G and every Sylow subgroup of B permutes with every maximal subgroup of every Sylow subgroup of A. If Gʹ is nilpotent, then ![]() $ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}} $.
$ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}} $.
An immediate consequence is:
Corollary C.
Let the group G = AB be a product of the subgroups A and B. Assume that A is a normal subgroup of G and every Sylow subgroup of B permutes with every maximal subgroup of every Sylow subgroup of A. If Gʹ is nilpotent, then ![]() $ G^{w \mathfrak{U}}=A^{w \mathfrak{U}}B^{w \mathfrak{U}} $.
$ G^{w \mathfrak{U}}=A^{w \mathfrak{U}}B^{w \mathfrak{U}} $.
Denote by ![]() $ \mathfrak{N} $ the class of all nilpotent groups. A nice result of Monakhov [Reference Monakhov7, Theorem 1] states that if G = AB is the mutually permutable product of the supersoluble subgroups A and B, then
$ \mathfrak{N} $ the class of all nilpotent groups. A nice result of Monakhov [Reference Monakhov7, Theorem 1] states that if G = AB is the mutually permutable product of the supersoluble subgroups A and B, then ![]() $ G^{\mathfrak{U}}=(G^\prime)^{\mathfrak{N}}=[A, B]^{\mathfrak{N}} $. We prove an analogue of this result for weak normal products.
$ G^{\mathfrak{U}}=(G^\prime)^{\mathfrak{N}}=[A, B]^{\mathfrak{N}} $. We prove an analogue of this result for weak normal products.
Corollary D.
Let G = AB be a weak normal product of the supersoluble subgroups A and B. If A is normal in G, we have that ![]() $G^{\mathfrak{U}}=(G^\prime)^{\mathfrak{N}}=[A,B]^{\mathfrak{N}}$.
$G^{\mathfrak{U}}=(G^\prime)^{\mathfrak{N}}=[A,B]^{\mathfrak{N}}$.
2. Preliminary results
It is easy to see that factor groups of weak normal products are also weak normal products. For weak direct products, we have the following:
Lemma 2.1. Let ![]() $ G =[A]B $ be a weak direct product of A and B.
$ G =[A]B $ be a weak direct product of A and B.
(a) If N is a normal subgroup of G such that
 $ N\leqslant A $ or
$ N\leqslant A $ or  $ N\leqslant B $, then
$ N\leqslant B $, then  $ G/N=[AN/N](BN/N) $ is a weak direct product of
$ G/N=[AN/N](BN/N) $ is a weak direct product of  $AN/N$ and
$AN/N$ and  $BN/N$.
$BN/N$.(b) If K is a subgroup of B, then
 $ [A]K $ is a weak direct product of A and K.
$ [A]K $ is a weak direct product of A and K.
Proof. (a) Let ![]() $H/N$ be a Sylow p-subgroup of
$H/N$ be a Sylow p-subgroup of ![]() $AN/N$. Then
$AN/N$. Then ![]() $H/N=PN/N$, where P is a Sylow p-subgroup of A. Let
$H/N=PN/N$, where P is a Sylow p-subgroup of A. Let ![]() $K/N$ be a maximal subgroup of
$K/N$ be a maximal subgroup of ![]() $H/N$. Then
$H/N$. Then ![]() $K=K\cap PN=N(P\cap K)$ and
$K=K\cap PN=N(P\cap K)$ and ![]() $K/N=N(P\cap K)/N$. Thus,
$K/N=N(P\cap K)/N$. Thus,
 \begin{equation*}p=|PN/N:(P\cap K)N/N|=\frac{|P||N|}{|P\cap N|} \frac{|P\cap K\cap N|}{|P\cap K| |N|}=|P: P\cap K|.\end{equation*}
\begin{equation*}p=|PN/N:(P\cap K)N/N|=\frac{|P||N|}{|P\cap N|} \frac{|P\cap K\cap N|}{|P\cap K| |N|}=|P: P\cap K|.\end{equation*} Hence, ![]() $P\cap K$ is a maximal subgroup of P. Then B permutes with
$P\cap K$ is a maximal subgroup of P. Then B permutes with ![]() $P\cap K$, and so
$P\cap K$, and so ![]() $BN/N$ permutes with
$BN/N$ permutes with ![]() $K/N$. Therefore,
$K/N$. Therefore, ![]() $ G/N=[AN/N](BN/N) $ is a weak direct product of
$ G/N=[AN/N](BN/N) $ is a weak direct product of ![]() $AN/N$ and
$AN/N$ and ![]() $BN/N$.
$BN/N$.
(b) Let K be any proper subgroup of B and H be any maximal subgroup of a Sylow subgroup of A. By the hypotheses, we have HB = BH and so ![]() $ H = H(A \cap B) = A \cap HB $. Since A is normal in G, it follows that H is normal in HB and so B normalizes H. Hence, K permutes with H. Therefore,
$ H = H(A \cap B) = A \cap HB $. Since A is normal in G, it follows that H is normal in HB and so B normalizes H. Hence, K permutes with H. Therefore, ![]() $ [A]K $ is a weak direct product of A and K.
$ [A]K $ is a weak direct product of A and K.
Our second lemma contains some of the properties of ![]() $\mathbb{P}$-subnormal subgroups.
$\mathbb{P}$-subnormal subgroups.
Lemma 2.2. [Reference Valisev, Valiseva and Tyutyanov8, Lemma 1.4]
Let G be a soluble group and H and K two subgroups of G. The following properties hold:
(i) If H is
 $\mathbb{P}$-subnormal in G and N is normal in G, then
$\mathbb{P}$-subnormal in G and N is normal in G, then  $HN/N$ is
$HN/N$ is  $\mathbb{P}$-subnormal in
$\mathbb{P}$-subnormal in  $G/N$.
$G/N$.(ii) If N is normal in G and
 $HN/N$ is
$HN/N$ is  $\mathbb{P}$-subnormal in
$\mathbb{P}$-subnormal in  $G/N$, then HN is
$G/N$, then HN is  $\mathbb{P}$-subnormal in G.
$\mathbb{P}$-subnormal in G.(iii) If H is
 $\mathbb{P}$-subnormal in K and K is
$\mathbb{P}$-subnormal in K and K is  $\mathbb{P}$-subnormal in G, then H is
$\mathbb{P}$-subnormal in G, then H is  $\mathbb{P}$-subnormal in G.
$\mathbb{P}$-subnormal in G.
3. Supersoluble and w-supersoluble residuals
We start this section by proving Theorem A.
Proof of Theorem A
Assume that the result is false, and let G be a counterexample of minimal order. Clearly, G is soluble and A and B are proper subgroups of G. Let N be a minimal normal subgroup of G contained in A, then applying Lemma 2.1(a), ![]() $G/N=[A/N] (BN/N)$ is a weak direct product of
$G/N=[A/N] (BN/N)$ is a weak direct product of ![]() $A/N$ and
$A/N$ and ![]() $BN/N$. By the minimality of G,
$BN/N$. By the minimality of G, ![]() $G/N \in \mathfrak{U}$. Since the class of all supersoluble groups is a saturated formation, there exists a unique minimal normal subgroup N of G contained in A, N a p-group for some prime p,
$G/N \in \mathfrak{U}$. Since the class of all supersoluble groups is a saturated formation, there exists a unique minimal normal subgroup N of G contained in A, N a p-group for some prime p, ![]() $|N| \gt p$ and
$|N| \gt p$ and ![]() $\Phi(A) = 1$. Since A is supersoluble, A has a normal Sylow subgroup, and since N is the unique minimal normal subgroup of G contained in A, it follows that
$\Phi(A) = 1$. Since A is supersoluble, A has a normal Sylow subgroup, and since N is the unique minimal normal subgroup of G contained in A, it follows that ![]() $\textbf{F}(A)$ is a p-group and
$\textbf{F}(A)$ is a p-group and ![]() $\textbf{F}(A)$ is an elementary abelian Sylow p-subgroup of A.
$\textbf{F}(A)$ is an elementary abelian Sylow p-subgroup of A.
Assume that A is not a p-group. Then ![]() $\textbf{F}(A)$ is a completely reducible A-module, and so
$\textbf{F}(A)$ is a completely reducible A-module, and so ![]() $ \textbf{F}(A) = N \times Z$, for some A-module Z. Let L be a minimal normal subgroup of A contained in N. Then
$ \textbf{F}(A) = N \times Z$, for some A-module Z. Let L be a minimal normal subgroup of A contained in N. Then ![]() $N = L \times D$, for some A-module D. Then
$N = L \times D$, for some A-module D. Then ![]() $\textbf{F}(A) = L \times DZ$, and DZ is a maximal subgroup of
$\textbf{F}(A) = L \times DZ$, and DZ is a maximal subgroup of ![]() $\textbf{F}(A)$ because L is of prime order. Therefore, E = DZ permutes with B. Hence,
$\textbf{F}(A)$ because L is of prime order. Therefore, E = DZ permutes with B. Hence, ![]() $ DZ=A\cap (DZ)B $, and so DZ is normalized by B. Since DZ is also normalized by A, it follows that DZ is a normal subgroup of G. The minimality of N forces D = 1 and so N is of prime order, which is a contradiction. Consequently, A is an elementary abelian p-group. Note that A cannot be cyclic since
$ DZ=A\cap (DZ)B $, and so DZ is normalized by B. Since DZ is also normalized by A, it follows that DZ is a normal subgroup of G. The minimality of N forces D = 1 and so N is of prime order, which is a contradiction. Consequently, A is an elementary abelian p-group. Note that A cannot be cyclic since ![]() $|N| \gt p$. Let
$|N| \gt p$. Let ![]() $1 \neq X$ be a maximal subgroup of A. Arguing as above, we have that X is normal in XB so that X is normalised by B. Hence X is normal in G because A is abelian. Therefore, N is contained in X, and so
$1 \neq X$ be a maximal subgroup of A. Arguing as above, we have that X is normal in XB so that X is normalised by B. Hence X is normal in G because A is abelian. Therefore, N is contained in X, and so ![]() $N \leq \Phi(A)= 1$, our final contradiction.
$N \leq \Phi(A)= 1$, our final contradiction.
Proof of Corollary A
Assume, by way of contradiction, that the result fails, and let G be a counterexample of least order. Clearly, G is soluble and A and B are proper subgroups of G. Since the class of all w-supersoluble groups is a saturated formation, we can argue as in Theorem A to conclude that there exists a unique minimal normal subgroup N of G contained in A, and N is a p-group for some prime p. Moreover, ![]() $\Phi(A) = 1$, and
$\Phi(A) = 1$, and ![]() $A_p = \textbf{F}(A)$ is the Sylow p-subgroup of A. By the minimality of G,
$A_p = \textbf{F}(A)$ is the Sylow p-subgroup of A. By the minimality of G, ![]() $G/N$ is w-supersoluble. Let P be a Sylow p-subgroup of G. Then
$G/N$ is w-supersoluble. Let P be a Sylow p-subgroup of G. Then ![]() $P/N$ is
$P/N$ is ![]() $\mathbb{P}$-subnormal in
$\mathbb{P}$-subnormal in ![]() $G/N$. By Lemma 2.2(ii), P is
$G/N$. By Lemma 2.2(ii), P is ![]() $\mathbb{P}$-subnormal in G. Suppose that for every prime q ≠ p dividing
$\mathbb{P}$-subnormal in G. Suppose that for every prime q ≠ p dividing ![]() $|G|$ and every Sylow q-subgroup B q of B, we have that AB q is a proper subgroup of G. Let A q be a Sylow q-subgroup of A such that
$|G|$ and every Sylow q-subgroup B q of B, we have that AB q is a proper subgroup of G. Let A q be a Sylow q-subgroup of A such that ![]() $G_{q}=A_{q}B_{q}$ is a Sylow q-subgroup of G. Since
$G_{q}=A_{q}B_{q}$ is a Sylow q-subgroup of G. Since ![]() $G/N$ is w-supersoluble, it follows that
$G/N$ is w-supersoluble, it follows that ![]() $G_{q}N$ is
$G_{q}N$ is ![]() $\mathbb{P}$-subnormal in G. By Lemma 2.1(b), AB q satisfies the hypotheses of the theorem. Hence, AB q is w-supersoluble by the choice of G. Thus,
$\mathbb{P}$-subnormal in G. By Lemma 2.1(b), AB q satisfies the hypotheses of the theorem. Hence, AB q is w-supersoluble by the choice of G. Thus, ![]() $G_{q}N \leq AB_{q}$ is w-supersoluble. Consequently, G q is
$G_{q}N \leq AB_{q}$ is w-supersoluble. Consequently, G q is ![]() $\mathbb{P}$-subnormal in
$\mathbb{P}$-subnormal in ![]() $G_{q}N$, which is
$G_{q}N$, which is ![]() $\mathbb{P}$-subnormal in G. Applying Lemma 2.2(iii), G q is
$\mathbb{P}$-subnormal in G. Applying Lemma 2.2(iii), G q is ![]() $\mathbb{P}$-subnormal in G. Therefore, the Sylow subgroups of G are
$\mathbb{P}$-subnormal in G. Therefore, the Sylow subgroups of G are ![]() $\mathbb{P}$-subnormal in G, and so G is w-supersoluble, a contradiction. Thus, we may assume there exists q ≠ p such that
$\mathbb{P}$-subnormal in G, and so G is w-supersoluble, a contradiction. Thus, we may assume there exists q ≠ p such that ![]() $G=AB_{q}$. Let
$G=AB_{q}$. Let ![]() $T=A_{p}G_{q}=(A_{p}A_{q})B_{q}$. Since A is normal in G, we have that A q is normal in G q and then
$T=A_{p}G_{q}=(A_{p}A_{q})B_{q}$. Since A is normal in G, we have that A q is normal in G q and then ![]() $A_{p}A_{q}$ is normalized by B q. Moreover,
$A_{p}A_{q}$ is normalized by B q. Moreover, ![]() $A_{p}A_{q}$ is a w-supersoluble metanilpotent subgroup of G. By [Reference Valisev, Valiseva and Tyutyanov8, Theorem 2.13(1)],
$A_{p}A_{q}$ is a w-supersoluble metanilpotent subgroup of G. By [Reference Valisev, Valiseva and Tyutyanov8, Theorem 2.13(1)], ![]() $A_{p}A_{q}$ is supersoluble. It is clear that T is a weak direct product of the supersoluble subgroups
$A_{p}A_{q}$ is supersoluble. It is clear that T is a weak direct product of the supersoluble subgroups ![]() $A_{p}A_{q}$ and B q. Applying Theorem A, it follows that T is supersoluble. Therefore, T is w-supersoluble. But
$A_{p}A_{q}$ and B q. Applying Theorem A, it follows that T is supersoluble. Therefore, T is w-supersoluble. But ![]() $G_{q}N \leq T$, which is w-supersoluble. Thus, G q is
$G_{q}N \leq T$, which is w-supersoluble. Thus, G q is ![]() $\mathbb{P}$-subnormal in
$\mathbb{P}$-subnormal in ![]() $G_{q}N$, which is
$G_{q}N$, which is ![]() $\mathbb{P}$-subnormal in G. Again the application of Lemma 2.2(iii) yields G q is
$\mathbb{P}$-subnormal in G. Again the application of Lemma 2.2(iii) yields G q is ![]() $\mathbb{P}$-subnormal in G. If G r is a Sylow r-subgroup of G for some prime
$\mathbb{P}$-subnormal in G. If G r is a Sylow r-subgroup of G for some prime ![]() $r \neq p, q$, then G r is contained in A and so G r is
$r \neq p, q$, then G r is contained in A and so G r is ![]() $\mathbb{P}$-subnormal in A. Since A is also
$\mathbb{P}$-subnormal in A. Since A is also ![]() $\mathbb{P}$-subnormal in G, we have that G r is
$\mathbb{P}$-subnormal in G, we have that G r is ![]() $\mathbb{P}$-subnormal in G. Consequently, every Sylow subgroup of G is
$\mathbb{P}$-subnormal in G. Consequently, every Sylow subgroup of G is ![]() $\mathbb{P}$-subnormal in G, and G is w-supersoluble. This final contradiction completes the proof of the corollary.
$\mathbb{P}$-subnormal in G, and G is w-supersoluble. This final contradiction completes the proof of the corollary.
Proof of Theorem B
Suppose that the result is not true, and let G be a minimal counterexample. Then
(i)
 $ A \in \mathfrak{F} $,
$ A \in \mathfrak{F} $,  $ B^{\mathfrak{F}}\not= 1 $,
$ B^{\mathfrak{F}}\not= 1 $,  $ {\rm Core}_{G}(B)=1 $ and
$ {\rm Core}_{G}(B)=1 $ and  $ G^{\mathfrak{F}}=B^{\mathfrak{F}}N $ for every minimal normal subgroup N of G such that
$ G^{\mathfrak{F}}=B^{\mathfrak{F}}N $ for every minimal normal subgroup N of G such that  $ N\leqslant A $.
$ N\leqslant A $.Let N be a minimal normal subgroup of G such that
 $ N\leqslant A $ or
$ N\leqslant A $ or  $ N\leqslant B $. Then
$ N\leqslant B $. Then  $ G/N=[AN/N](BN/N) $ is a weak direct product of
$ G/N=[AN/N](BN/N) $ is a weak direct product of  $AN/N$ and
$AN/N$ and  $BN/N$ by Lemma 2.1(a). The minimal choice of G implies that
$BN/N$ by Lemma 2.1(a). The minimal choice of G implies that  $ G^{\mathfrak{F}}N/N=(A^{\mathfrak{F}}N/N) (B^{\mathfrak{F}}N/N) $, that is,
$ G^{\mathfrak{F}}N/N=(A^{\mathfrak{F}}N/N) (B^{\mathfrak{F}}N/N) $, that is,  $ G^{\mathfrak{F}}N=A^{\mathfrak{F}}B^{\mathfrak{F}}N $. Since
$ G^{\mathfrak{F}}N=A^{\mathfrak{F}}B^{\mathfrak{F}}N $. Since  $ G/G^{\mathfrak{F}}\in \mathfrak{F} $,
$ G/G^{\mathfrak{F}}\in \mathfrak{F} $,  $ AG^{\mathfrak{F}}/G^{\mathfrak{F}} $ and
$ AG^{\mathfrak{F}}/G^{\mathfrak{F}} $ and  $ BG^{\mathfrak{F}}/G^{\mathfrak{F}} $ also belong to
$ BG^{\mathfrak{F}}/G^{\mathfrak{F}} $ also belong to  $ \mathfrak{F} $ and then
$ \mathfrak{F} $ and then  $ A^{\mathfrak{F}}\leqslant G^{\mathfrak{F}} $ and
$ A^{\mathfrak{F}}\leqslant G^{\mathfrak{F}} $ and  $ B^{\mathfrak{F}}\leqslant G^{\mathfrak{F}} $. If
$ B^{\mathfrak{F}}\leqslant G^{\mathfrak{F}} $. If  $ G^{\mathfrak{F}}\cap N= 1 $, then
$ G^{\mathfrak{F}}\cap N= 1 $, then  $ G^{\mathfrak{F}}=A^{\mathfrak{F}}B^{\mathfrak{F}}(G^{\mathfrak{F}}\cap N)=A^{\mathfrak{F}}B^{\mathfrak{F}} $, a contradiction. Hence,
$ G^{\mathfrak{F}}=A^{\mathfrak{F}}B^{\mathfrak{F}}(G^{\mathfrak{F}}\cap N)=A^{\mathfrak{F}}B^{\mathfrak{F}} $, a contradiction. Hence,  $ G^{\mathfrak{F}}=A^{\mathfrak{F}}B^{\mathfrak{F}} N $ for every minimal normal subgroup N of G such that
$ G^{\mathfrak{F}}=A^{\mathfrak{F}}B^{\mathfrak{F}} N $ for every minimal normal subgroup N of G such that  $ N\leqslant A $ or
$ N\leqslant A $ or  $ N\leqslant B $. If
$ N\leqslant B $. If  $A^{\mathfrak{F}} \neq 1$, then there exists a minimal normal subgroup N of G contained in
$A^{\mathfrak{F}} \neq 1$, then there exists a minimal normal subgroup N of G contained in  $A^{\mathfrak{F}}$ because
$A^{\mathfrak{F}}$ because  $A^{\mathfrak{F}}$ is normal in G. This contradiction yields
$A^{\mathfrak{F}}$ is normal in G. This contradiction yields  $A \in \mathfrak{F}$ and
$A \in \mathfrak{F}$ and  $ G^{\mathfrak{F}}=B^{\mathfrak{F}}N $ for every minimal normal subgroup N of G such that
$ G^{\mathfrak{F}}=B^{\mathfrak{F}}N $ for every minimal normal subgroup N of G such that  $ N\leqslant A $ or
$ N\leqslant A $ or  $ N\leqslant B $. If
$ N\leqslant B $. If  $ B \in \mathfrak{F} $, then
$ B \in \mathfrak{F} $, then  $ G\in \mathfrak{F} $ by Theorem A and Corollary A, contrary to the assumption. Hence,
$ G\in \mathfrak{F} $ by Theorem A and Corollary A, contrary to the assumption. Hence,  $ B^{\mathfrak{F}} \neq 1 $. Suppose that
$ B^{\mathfrak{F}} \neq 1 $. Suppose that  $Core_{G}(B) \neq 1$. Let N be a minimal normal subgroup of G contained in B, and let R be a minimal normal subgroup of G contained in A. Then
$Core_{G}(B) \neq 1$. Let N be a minimal normal subgroup of G contained in B, and let R be a minimal normal subgroup of G contained in A. Then  $G^{\mathfrak{F}}=B^{\mathfrak{F}}N \cap B^{\mathfrak{F}}R \leq B \cap B^{\mathfrak{F}}R=B^{\mathfrak{F}}(B \cap R)=B^{\mathfrak{F}}$, a contradiction. Consequently, we have that
$G^{\mathfrak{F}}=B^{\mathfrak{F}}N \cap B^{\mathfrak{F}}R \leq B \cap B^{\mathfrak{F}}R=B^{\mathfrak{F}}(B \cap R)=B^{\mathfrak{F}}$, a contradiction. Consequently, we have that  ${\rm Core}_{G}(B)=1$.
${\rm Core}_{G}(B)=1$.(ii)
 $ \mathbf{F}(A)$ is a Sylow p-subgroup of A, where p is the largest prime dividing
$ \mathbf{F}(A)$ is a Sylow p-subgroup of A, where p is the largest prime dividing  $ |A| $ .
$ |A| $ .Since
 $ A \in \mathfrak{F} $, it follows that A is a Sylow tower group of supersoluble type. In particular,
$ A \in \mathfrak{F} $, it follows that A is a Sylow tower group of supersoluble type. In particular,  $ 1 \neq \mathbf{O}_{p}(A)$ is the Sylow p-subgroup of A, where p is the largest prime dividing
$ 1 \neq \mathbf{O}_{p}(A)$ is the Sylow p-subgroup of A, where p is the largest prime dividing  $ |A| $. If
$ |A| $. If  $ \mathbf{F}(A) $ is not a p-group, then
$ \mathbf{F}(A) $ is not a p-group, then  $1 \neq \mathbf{O}_{q}(A)\leqslant \mathbf{O}_{q}(G)$. Let N 1 be a minimal normal subgroup of G contained in
$1 \neq \mathbf{O}_{q}(A)\leqslant \mathbf{O}_{q}(G)$. Let N 1 be a minimal normal subgroup of G contained in  $\mathbf{O}_{p}(A) $, and let N 2 be a minimal normal subgroup of G contained in
$\mathbf{O}_{p}(A) $, and let N 2 be a minimal normal subgroup of G contained in  $\mathbf{O}_{q}(A) $. Then
$\mathbf{O}_{q}(A) $. Then  $ G^{\mathfrak{F}}=B^{\mathfrak{F}}N_{1}=B^{\mathfrak{F}}N_{2}$, which is a contradiction since
$ G^{\mathfrak{F}}=B^{\mathfrak{F}}N_{1}=B^{\mathfrak{F}}N_{2}$, which is a contradiction since  $ B^{\mathfrak{F}}\cap N_{1}=B^{\mathfrak{F}}\cap N_{2}=1 $. Therefore,
$ B^{\mathfrak{F}}\cap N_{1}=B^{\mathfrak{F}}\cap N_{2}=1 $. Therefore,  $ \mathbf{F}(A) = \mathbf{O}_{p}(A)$ is the Sylow p-subgroup of A.
$ \mathbf{F}(A) = \mathbf{O}_{p}(A)$ is the Sylow p-subgroup of A.(iii) G is soluble, AK belongs to
 $ \mathfrak{F} $ for every proper subgroup K of B; in particular, B is a minimal non-supersoluble group and
$ \mathfrak{F} $ for every proper subgroup K of B; in particular, B is a minimal non-supersoluble group and  $ B^{\mathfrak{F}} $ is a q-subgroup of B for some prime q.
$ B^{\mathfrak{F}} $ is a q-subgroup of B for some prime q.Suppose that K is a proper subgroup of B. By Lemma 2.1, AK satisfies the hypotheses of the theorem, and so
 $ (AK)^{\mathfrak{F}}=K^{\mathfrak{F}} $ by the minimal choice of G. Since
$ (AK)^{\mathfrak{F}}=K^{\mathfrak{F}} $ by the minimal choice of G. Since  $ (AK^{x})^{\mathfrak{F}}=(K^{x})^{\mathfrak {F}}=(K^{\mathfrak{F}})^{x} $ for any
$ (AK^{x})^{\mathfrak{F}}=(K^{x})^{\mathfrak {F}}=(K^{\mathfrak{F}})^{x} $ for any  $ x\in B $, it follows that A normalizes
$ x\in B $, it follows that A normalizes  $ (K^{\mathfrak{F}})^{x} $. Thus, A normalizes
$ (K^{\mathfrak{F}})^{x} $. Thus, A normalizes  $ \langle (K^{\mathfrak{F}})^{x} \mid x\in B \rangle $. Then
$ \langle (K^{\mathfrak{F}})^{x} \mid x\in B \rangle $. Then  $ \langle (K^{\mathfrak{F}})^{x} \mid x\in B \rangle \lhd G $, contrary to
$ \langle (K^{\mathfrak{F}})^{x} \mid x\in B \rangle \lhd G $, contrary to  $ {\rm Core}_{G}(B)=1 $. Hence,
$ {\rm Core}_{G}(B)=1 $. Hence,  $ (K^{\mathfrak{F}})^{x}=1 $. Consequently, AK belongs to
$ (K^{\mathfrak{F}})^{x}=1 $. Consequently, AK belongs to  $ \mathfrak{F} $. This shows that B is
$ \mathfrak{F} $. This shows that B is  $ \mathfrak{F} $-critical, and by [Reference Valisev, Valiseva and Tyutyanov8, Theorem 2.9], we have that B is a minimal non-supersoluble group. By [Reference Ballester-Bolinches and Esteban-Romero3, Theorem 10], we have that
$ \mathfrak{F} $-critical, and by [Reference Valisev, Valiseva and Tyutyanov8, Theorem 2.9], we have that B is a minimal non-supersoluble group. By [Reference Ballester-Bolinches and Esteban-Romero3, Theorem 10], we have that  $ B^{\mathfrak{F}} $ is a q-group for some prime q. In particular, B and then G are soluble.
$ B^{\mathfrak{F}} $ is a q-group for some prime q. In particular, B and then G are soluble.(iv)
 $ G^{\mathfrak{F}}=B^{\mathfrak{F}}\times N $ is an elementary abelian p -group.
$ G^{\mathfrak{F}}=B^{\mathfrak{F}}\times N $ is an elementary abelian p -group.Applying (iii), it follows that
 $B^{\mathfrak{F}}$ is a q-group for some prime q. Let N be a minimal normal subgroup of G contained in A. Then
$B^{\mathfrak{F}}$ is a q-group for some prime q. Let N be a minimal normal subgroup of G contained in A. Then  $G^{\mathfrak{F}}=B^{\mathfrak{F}}N$ by (i), and N is a p-group by (ii).
$G^{\mathfrak{F}}=B^{\mathfrak{F}}N$ by (i), and N is a p-group by (ii).Suppose that
 $B^{\mathfrak{F}}$ is a normal subgroup of
$B^{\mathfrak{F}}$ is a normal subgroup of  $G^{\mathfrak{F}}$. Then
$G^{\mathfrak{F}}$. Then  $G^{\mathfrak{F}}/B^{\mathfrak{F}}$ is an elementary abelian p-group. Consequently, the residual X of
$G^{\mathfrak{F}}/B^{\mathfrak{F}}$ is an elementary abelian p-group. Consequently, the residual X of  $G^{\mathfrak{F}}$ associated to the formation of all elementary abelian p-groups is a normal subgroup of G contained in B. Hence,
$G^{\mathfrak{F}}$ associated to the formation of all elementary abelian p-groups is a normal subgroup of G contained in B. Hence,  $X \leq {\rm Core}_G(B) = 1$, and
$X \leq {\rm Core}_G(B) = 1$, and  $G^{\mathfrak{F}}$ is an elementary abelian p-group.
$G^{\mathfrak{F}}$ is an elementary abelian p-group.Assume that p ≠ q. Let N be a minimal normal subgroup of G contained in A. Then
 $G^{\mathfrak{F}}=B^{\mathfrak{F}}N$, and N is a p-group by (ii). Hence,
$G^{\mathfrak{F}}=B^{\mathfrak{F}}N$, and N is a p-group by (ii). Hence,  $B^{\mathfrak{F}}$ is a Sylow q-subgroup of
$B^{\mathfrak{F}}$ is a Sylow q-subgroup of  $ G^{\mathfrak{F}}=B^{\mathfrak{F}}N $. Applying Frattini’s argument, we have that
$ G^{\mathfrak{F}}=B^{\mathfrak{F}}N $. Applying Frattini’s argument, we have that  $G=G^{\mathfrak{F}}N_{G}(B^{\mathfrak{F}})=NN_{G}(B^{\mathfrak{F}})$. Since
$G=G^{\mathfrak{F}}N_{G}(B^{\mathfrak{F}})=NN_{G}(B^{\mathfrak{F}})$. Since  ${\rm Core}_{G}(B)=1$, it follows that
${\rm Core}_{G}(B)=1$, it follows that  $N_{G}(B^{\mathfrak{F}})$ is a proper subgroup of G. Hence, N is not contained in
$N_{G}(B^{\mathfrak{F}})$ is a proper subgroup of G. Hence, N is not contained in  $\Phi(G)$ for each minimal normal subgroup N of G contained in A. If
$\Phi(G)$ for each minimal normal subgroup N of G contained in A. If  $\Phi(A) \neq 1$, a minimal normal subgroup of G must be contained in
$\Phi(A) \neq 1$, a minimal normal subgroup of G must be contained in  $\Phi(A) \leq \Phi(G)$, a contradiction. Therefore,
$\Phi(A) \leq \Phi(G)$, a contradiction. Therefore,  $\Phi(A)=1$. Let N be a minimal normal subgroup of G contained in A. Then
$\Phi(A)=1$. Let N be a minimal normal subgroup of G contained in A. Then  $N=N_{1} \times N_{2} \times \cdots \times N_{r}$ is a direct product of minimal normal subgroups of A, and there exists
$N=N_{1} \times N_{2} \times \cdots \times N_{r}$ is a direct product of minimal normal subgroups of A, and there exists  $i \in \{1,2, \dots, r \}$ such that N i is not contained in
$i \in \{1,2, \dots, r \}$ such that N i is not contained in  $ \Phi(A)$. Suppose i = 1. Let M be a maximal subgroup of A such that
$ \Phi(A)$. Suppose i = 1. Let M be a maximal subgroup of A such that  $A=N_{1}M$ and
$A=N_{1}M$ and  $N_{1} \cap M=1$. Assume first that A is a p-group. Then BM is a subgroup of G, and
$N_{1} \cap M=1$. Assume first that A is a p-group. Then BM is a subgroup of G, and  $M=BM \cap A$ is a normal subgroup of BM. Hence, M is normalized by B, and so M is a normal subgroup of G. Now
$M=BM \cap A$ is a normal subgroup of BM. Hence, M is normalized by B, and so M is a normal subgroup of G. Now  $N=N_{1}(M \cap N)$. But
$N=N_{1}(M \cap N)$. But  $M \cap N$ is normal in G. The minimality of N yields
$M \cap N$ is normal in G. The minimality of N yields  $N=N_{1}$ and then
$N=N_{1}$ and then  $|N|=p$. Thus,
$|N|=p$. Thus,  $G/C_{G}(N)$ is abelian. Hence,
$G/C_{G}(N)$ is abelian. Hence,  $G^{\mathfrak{F}}$ centralizes N, and
$G^{\mathfrak{F}}$ centralizes N, and  $B^{\mathfrak{F}}$ is a normal subgroup in
$B^{\mathfrak{F}}$ is a normal subgroup in  $G^{\mathfrak{F}}$, and so
$G^{\mathfrak{F}}$, and so  $G^{\mathfrak{F}}$ is an elementary abelian p-group. This contradiction implies that A is not a p-group. Then
$G^{\mathfrak{F}}$ is an elementary abelian p-group. This contradiction implies that A is not a p-group. Then  $T= \mathbf{F}(A)B$ is a proper subgroup of G which is a weak direct product of
$T= \mathbf{F}(A)B$ is a proper subgroup of G which is a weak direct product of  $ \mathbf{F}(A)$ and B. By the minimality of G,
$ \mathbf{F}(A)$ and B. By the minimality of G,  $T^{\mathfrak{F}}=B^{\mathfrak{F}}$. Then
$T^{\mathfrak{F}}=B^{\mathfrak{F}}$. Then  $B^{\mathfrak{F}}$ is a normal subgroup of
$B^{\mathfrak{F}}$ is a normal subgroup of  $G^{\mathfrak{F}}$, and so
$G^{\mathfrak{F}}$, and so  $G^{\mathfrak{F}}$ is an elementary abelian p-group, a contradiction which shows that p = q. Then
$G^{\mathfrak{F}}$ is an elementary abelian p-group, a contradiction which shows that p = q. Then  $B^{\mathfrak{F}}$ is a subnormal subgroup of G. By [Reference Doerk and Hawkes6, Lemma A.14.3], N normalizes
$B^{\mathfrak{F}}$ is a subnormal subgroup of G. By [Reference Doerk and Hawkes6, Lemma A.14.3], N normalizes  $B^{\mathfrak{F}}$, and therefore
$B^{\mathfrak{F}}$, and therefore  $B^{\mathfrak{F}}$ is a normal subgroup of the elementary abelian p-group
$B^{\mathfrak{F}}$ is a normal subgroup of the elementary abelian p-group  $G^{\mathfrak{F}}$.
$G^{\mathfrak{F}}$.(v) Final contradiction. By [Reference Doerk and Hawkes6, IV, 5.18], since
 $ B^{\mathfrak{F}} $ is abelian, there exists an
$ B^{\mathfrak{F}} $ is abelian, there exists an  $ \mathfrak{F} $-projector K of B such that
$ \mathfrak{F} $-projector K of B such that  $ B=B^{\mathfrak{F}}K $ and
$ B=B^{\mathfrak{F}}K $ and  $ K\cap B^{\mathfrak{F}}=1 $. Consider the subgroup Z = AK of G. Applying (iii), Z belongs to
$ K\cap B^{\mathfrak{F}}=1 $. Consider the subgroup Z = AK of G. Applying (iii), Z belongs to  $ \mathfrak{F} $ and
$ \mathfrak{F} $ and  $G=B^{\mathfrak{F}}Z=F(G)Z$. By [Reference Doerk and Hawkes6, III, 3.23(b)], there exists a unique
$G=B^{\mathfrak{F}}Z=F(G)Z$. By [Reference Doerk and Hawkes6, III, 3.23(b)], there exists a unique  $\mathfrak{F}$-projector of G containing Z, E say. Hence,
$\mathfrak{F}$-projector of G containing Z, E say. Hence,  $G=B^{\mathfrak{F}}Z=G^{\mathfrak{F}}E$ and
$G=B^{\mathfrak{F}}Z=G^{\mathfrak{F}}E$ and  $G^{\mathfrak{F}} \cap E=1$ by (iii) and [Reference Doerk and Hawkes6, IV, 5.18]. In particular,
$G^{\mathfrak{F}} \cap E=1$ by (iii) and [Reference Doerk and Hawkes6, IV, 5.18]. In particular,  $B^{\mathfrak{F}} \cap Z=1$. Now
$B^{\mathfrak{F}} \cap Z=1$. Now  $|Z||B^{\mathfrak{F}}|=|E| |G^{\mathfrak{F}} |=|E||B^{\mathfrak{F}}| |N |$. Hence,
$|Z||B^{\mathfrak{F}}|=|E| |G^{\mathfrak{F}} |=|E||B^{\mathfrak{F}}| |N |$. Hence,  $|Z |=|E| |N| $. This implies Z = E and then
$|Z |=|E| |N| $. This implies Z = E and then  $B^{\mathfrak{F}}=G^{\mathfrak{F}}$, a contradiction.
$B^{\mathfrak{F}}=G^{\mathfrak{F}}$, a contradiction.
Proof of Theorem C
Assume that the result is false and let G be a minimal counterexample. Then every proper epimorphic image of G is supersoluble, and hence G has exactly one minimal normal subgroup N which is not contained in the Frattini subgroup of G. Since G is soluble, it follows that N is abelian, ![]() $N=C_{G}(N)=F(G)$, and there exists a core-free maximal subgroup of G such that G = NM and
$N=C_{G}(N)=F(G)$, and there exists a core-free maximal subgroup of G such that G = NM and ![]() $N \cap M = 1$. Let p be the prime dividing
$N \cap M = 1$. Let p be the prime dividing ![]() $|N|$. Then
$|N|$. Then ![]() $|N| \gt p$. Since
$|N| \gt p$. Since ![]() $1 \neq G^\prime$ is nilpotent, we have that
$1 \neq G^\prime$ is nilpotent, we have that ![]() $G^\prime=N$ and M is abelian. However,
$G^\prime=N$ and M is abelian. However, ![]() $\mathbf{O}_{p}(M) = 1$ by [Reference Doerk and Hawkes6, Lemma A.13.6]. Hence, M is a p ʹ-group and N is the Sylow p-subgroup of G. Since B ≠ G, we have that
$\mathbf{O}_{p}(M) = 1$ by [Reference Doerk and Hawkes6, Lemma A.13.6]. Hence, M is a p ʹ-group and N is the Sylow p-subgroup of G. Since B ≠ G, we have that ![]() $N \leq A$. Note that
$N \leq A$. Note that ![]() $N = C_{A}(N) = \mathbf{O}_{p^{\prime}p}(A)$. Therefore,
$N = C_{A}(N) = \mathbf{O}_{p^{\prime}p}(A)$. Therefore, ![]() $A/\mathbf{O}_{p^{\prime}p}(A)=A/\mathbf{O}_{p}(A)= A/N$ is abelian of exponent dividing p − 1 because A is supersoluble. Assume BN is a proper subgroup of G. Then, by the minimality of G, BN is supersoluble, and so
$A/\mathbf{O}_{p^{\prime}p}(A)=A/\mathbf{O}_{p}(A)= A/N$ is abelian of exponent dividing p − 1 because A is supersoluble. Assume BN is a proper subgroup of G. Then, by the minimality of G, BN is supersoluble, and so ![]() $B_{p^\prime} \cong BN/\mathbf{O}_{p^{\prime}p}(BN)$ is abelian of exponent dividing p − 1. Consequently, M is abelian of exponent dividing p − 1. Since N is an irreducible and faithful module for M, we have that N has order p by [Reference Doerk and Hawkes6, Theorem B.9.8], a contradiction. Hence, G = BN. Now
$B_{p^\prime} \cong BN/\mathbf{O}_{p^{\prime}p}(BN)$ is abelian of exponent dividing p − 1. Consequently, M is abelian of exponent dividing p − 1. Since N is an irreducible and faithful module for M, we have that N has order p by [Reference Doerk and Hawkes6, Theorem B.9.8], a contradiction. Hence, G = BN. Now ![]() $B \cap N$ is a normal subgroup of G contained in N. Thus,
$B \cap N$ is a normal subgroup of G contained in N. Thus, ![]() $B \cap N=1$, and G = BN is the weak direct product of B and N. By Theorem A, G is supersoluble. This contradiction proves the theorem.
$B \cap N=1$, and G = BN is the weak direct product of B and N. By Theorem A, G is supersoluble. This contradiction proves the theorem.
Proof of Corollary B
Note that since Gʹ is nilpotent, A and B are metanilpotent. By [Reference Valisev, Valiseva and Tyutyanov8, Theorem 2.11], A and B are supersoluble. By Theorem C, G is supersoluble, and hence ![]() $ G\in w \mathfrak{U} $.
$ G\in w \mathfrak{U} $.
Proof of Theorem D
Suppose the theorem is not true and let ![]() $ (G, A, B) $ be a counterexample with
$ (G, A, B) $ be a counterexample with ![]() $ |G| + |A| + |B| $ as small as possible. Let N be a minimal normal subgroup of G. It is easy to check that
$ |G| + |A| + |B| $ as small as possible. Let N be a minimal normal subgroup of G. It is easy to check that ![]() $ G/N $ satisfies the hypotheses of the theorem. By the minimality of G, we have that
$ G/N $ satisfies the hypotheses of the theorem. By the minimality of G, we have that ![]() $ G^{\mathfrak{U}}N=A^{\mathfrak{U}}B^{\mathfrak{U}}N $. Hence,
$ G^{\mathfrak{U}}N=A^{\mathfrak{U}}B^{\mathfrak{U}}N $. Hence, ![]() $ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}}(G^{\mathfrak{U}}\cap N) $. Consequently,
$ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}}(G^{\mathfrak{U}}\cap N) $. Consequently, ![]() $ {\rm Soc}(G) $ is contained in
$ {\rm Soc}(G) $ is contained in ![]() $ G^{\mathfrak{U}} $ and
$ G^{\mathfrak{U}} $ and ![]() $ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}}N $ for every minimal normal subgroup N of G. Since
$ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}}N $ for every minimal normal subgroup N of G. Since ![]() $ G^{\mathfrak{U}}$ is contained in Gʹ, we have that
$ G^{\mathfrak{U}}$ is contained in Gʹ, we have that ![]() $ G^{\mathfrak{U}}$ is nilpotent.
$ G^{\mathfrak{U}}$ is nilpotent.
Note that ![]() $A^{\mathfrak{U}}$ is a normal subgroup of G. If
$A^{\mathfrak{U}}$ is a normal subgroup of G. If ![]() $ A^{\mathfrak{U}}\not= 1 $, then there exists a minimal normal subgroup N of G such that
$ A^{\mathfrak{U}}\not= 1 $, then there exists a minimal normal subgroup N of G such that ![]() $N \leq A^{\mathfrak{U}} $ and so
$N \leq A^{\mathfrak{U}} $ and so ![]() $ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}}N=A^{\mathfrak{U}}B^{\mathfrak{U}} $, a contradiction. Hence, we may assume that A is supersoluble and that
$ G^{\mathfrak{U}}=A^{\mathfrak{U}}B^{\mathfrak{U}}N=A^{\mathfrak{U}}B^{\mathfrak{U}} $, a contradiction. Hence, we may assume that A is supersoluble and that ![]() $ G^{\mathfrak{U}}=B^{\mathfrak{U}}N $ for every minimal normal subgroup N of G. If B were supersoluble, then G would be supersoluble by Theorem C, which is a contradiction. Hence,
$ G^{\mathfrak{U}}=B^{\mathfrak{U}}N $ for every minimal normal subgroup N of G. If B were supersoluble, then G would be supersoluble by Theorem C, which is a contradiction. Hence, ![]() $ B^{\mathfrak{U}} \neq 1$. Furthermore,
$ B^{\mathfrak{U}} \neq 1$. Furthermore, ![]() $ B^{\mathfrak{U}} $ cannot contain a normal subgroup of G. Hence,
$ B^{\mathfrak{U}} $ cannot contain a normal subgroup of G. Hence, ![]() $ {\rm Core}_{G}(B^{\mathfrak{U}})=1 $. Let p be the largest prime dividing
$ {\rm Core}_{G}(B^{\mathfrak{U}})=1 $. Let p be the largest prime dividing ![]() $ |A| $. Since A is a Sylow tower group of supersoluble type, A has a normal Sylow p-subgroup, A p say, which is also normal in G. Hence, G has a minimal normal subgroup N of G which is a p-group. Since
$ |A| $. Since A is a Sylow tower group of supersoluble type, A has a normal Sylow p-subgroup, A p say, which is also normal in G. Hence, G has a minimal normal subgroup N of G which is a p-group. Since ![]() $G^{\mathfrak{U}}$ is nilpotent, we have that
$G^{\mathfrak{U}}$ is nilpotent, we have that ![]() $B^{\mathfrak{U}}$ is a subnormal subgroup of G. By [Reference Doerk and Hawkes6, Lemma A.14.3],
$B^{\mathfrak{U}}$ is a subnormal subgroup of G. By [Reference Doerk and Hawkes6, Lemma A.14.3], ![]() $B^{\mathfrak{U}}$ is normalized by N. Thus,
$B^{\mathfrak{U}}$ is normalized by N. Thus, ![]() $B^{\mathfrak{U}}$ is a normal subgroup of
$B^{\mathfrak{U}}$ is a normal subgroup of ![]() $G^{\mathfrak{U}}$, and
$G^{\mathfrak{U}}$, and ![]() $ G^{\mathfrak{U}}/B^{\mathfrak{U}} $ is an elementary abelian p-group. Consequently
$ G^{\mathfrak{U}}/B^{\mathfrak{U}} $ is an elementary abelian p-group. Consequently ![]() $ B^{\mathfrak{U}} $ contains the residual X of
$ B^{\mathfrak{U}} $ contains the residual X of ![]() $ G^{\mathfrak{U}}$ associated to the formation of all elementary abelian p-groups. Since X is a normal subgroup of G, it follows that
$ G^{\mathfrak{U}}$ associated to the formation of all elementary abelian p-groups. Since X is a normal subgroup of G, it follows that ![]() $X \leq {\rm Core}_{G}(B^{\mathfrak{U}})=1$. Hence,
$X \leq {\rm Core}_{G}(B^{\mathfrak{U}})=1$. Hence, ![]() $ G^{\mathfrak{U}} $ is an elementary abelian p-group.
$ G^{\mathfrak{U}} $ is an elementary abelian p-group.
Since ![]() $ {\rm Soc}(G) $ is contained in
$ {\rm Soc}(G) $ is contained in ![]() $ G^{\mathfrak{U}} $,
$ G^{\mathfrak{U}} $, ![]() $ \textbf{O}_{p^\prime}(G)=1 $ and hence
$ \textbf{O}_{p^\prime}(G)=1 $ and hence ![]() $ \mathbf{F}(G)=\textbf{O}_{p}(G) $. Therefore
$ \mathbf{F}(G)=\textbf{O}_{p}(G) $. Therefore ![]() $ G^\prime \leq \mathbf{F}(G) $ is a p-group, and
$ G^\prime \leq \mathbf{F}(G) $ is a p-group, and ![]() $ \mathbf{F}(G) $ is the unique Sylow p-subgroup of G. Moreover, the Hall p ʹ-subgroups of G are abelian (note that G is soluble). Assume
$ \mathbf{F}(G) $ is the unique Sylow p-subgroup of G. Moreover, the Hall p ʹ-subgroups of G are abelian (note that G is soluble). Assume ![]() $ A_{p}B \lt G $. Then
$ A_{p}B \lt G $. Then ![]() $ A_{p}B $ satisfies the hypotheses of the theorem. By the choice of G, we have that
$ A_{p}B $ satisfies the hypotheses of the theorem. By the choice of G, we have that ![]() $ (A_{p}B)^{\mathfrak{U}}=B^{\mathfrak{U}} $. Note that
$ (A_{p}B)^{\mathfrak{U}}=B^{\mathfrak{U}} $. Note that ![]() $G^\prime \leq A_{p}B $. Hence,
$G^\prime \leq A_{p}B $. Hence, ![]() $A_{p}B$ is a normal subgroup of G. This implies that
$A_{p}B$ is a normal subgroup of G. This implies that ![]() $ B^{\mathfrak{U}} $ is normal in G, a contradiction. Hence,
$ B^{\mathfrak{U}} $ is normal in G, a contradiction. Hence, ![]() $ G=A_{p}B$ and A p and B satisfy the hypotheses of the theorem. If
$ G=A_{p}B$ and A p and B satisfy the hypotheses of the theorem. If ![]() $A \neq A_{p}$, the choice of
$A \neq A_{p}$, the choice of ![]() $(G, A, B)$ implies that
$(G, A, B)$ implies that ![]() $ G^{\mathfrak{U}}=B^{\mathfrak{U}} $, a contradiction. Consequently, we have that
$ G^{\mathfrak{U}}=B^{\mathfrak{U}} $, a contradiction. Consequently, we have that ![]() $A=A_{p}$.
$A=A_{p}$.
Write ![]() $T=AB_{p^\prime}$. By Theorem C, T is supersoluble. Moreover, since
$T=AB_{p^\prime}$. By Theorem C, T is supersoluble. Moreover, since ![]() $G=F(G)B_{p^\prime}$, it follows that every minimal normal subgroup N of G contained in T is a minimal normal subgroup of T. Thus,
$G=F(G)B_{p^\prime}$, it follows that every minimal normal subgroup N of G contained in T is a minimal normal subgroup of T. Thus, ![]() $|N|=p$. Consequently, N is
$|N|=p$. Consequently, N is ![]() ${\mathfrak{U}}$-central in G. By [Reference Doerk and Hawkes6, V, 3.2], N is contained in every supersoluble normalizer of G. Let E be one of them. Then
${\mathfrak{U}}$-central in G. By [Reference Doerk and Hawkes6, V, 3.2], N is contained in every supersoluble normalizer of G. Let E be one of them. Then ![]() $G=G^{\mathfrak{U}}E$ and
$G=G^{\mathfrak{U}}E$ and ![]() $G^{\mathfrak{U}} \cap E=1$. However,
$G^{\mathfrak{U}} \cap E=1$. However, ![]() $N \leq G^{\mathfrak{U}} \cap E=1$. This final contradiction proves the theorem.
$N \leq G^{\mathfrak{U}} \cap E=1$. This final contradiction proves the theorem.
Proof of Corollary C
Since ![]() $\mathfrak{U}\subseteq w\mathfrak{U}$, we have
$\mathfrak{U}\subseteq w\mathfrak{U}$, we have ![]() $G^{w\mathfrak{U}} \leq G^{\mathfrak{U}} \leq G^\prime$. Then
$G^{w\mathfrak{U}} \leq G^{\mathfrak{U}} \leq G^\prime$. Then ![]() $G/G^{w\mathfrak{U}}$ is a metanilpotent w-supersoluble group. Applying [Reference Valisev, Valiseva and Tyutyanov8, Theorem 2.11], we have that
$G/G^{w\mathfrak{U}}$ is a metanilpotent w-supersoluble group. Applying [Reference Valisev, Valiseva and Tyutyanov8, Theorem 2.11], we have that ![]() $G/G^{w\mathfrak{U}}$ is supersoluble. Hence,
$G/G^{w\mathfrak{U}}$ is supersoluble. Hence, ![]() $G^{\mathfrak{U}} \leq G^{w \mathfrak{U}}$, and therefore
$G^{\mathfrak{U}} \leq G^{w \mathfrak{U}}$, and therefore ![]() $G^{\mathfrak{U}} = G^{w \mathfrak{U}}$, and the same is true for A and B. Therefore, by Theorem D,
$G^{\mathfrak{U}} = G^{w \mathfrak{U}}$, and the same is true for A and B. Therefore, by Theorem D, ![]() $ G^{w \mathfrak{U}}=A^{w \mathfrak{U}}B^{w \mathfrak{U}} $, as desired.
$ G^{w \mathfrak{U}}=A^{w \mathfrak{U}}B^{w \mathfrak{U}} $, as desired.
4. An analogue of Monakhov’s result
The following two results are the key to prove Corollary D.
Lemma 4.1. [Reference Ballester-Bolinches and Pedraza-Aguilera4, Theorem A]
Let the group G = HK be the product of the subgroups H and K. Assume that H permutes with every maximal subgroup of K and K permutes with every maximal subgroup of H. If H is supersoluble, K is nilpotent and K is δ-permutable in H, where δ is a complete set of Sylow subgroups of H, then G is supersoluble.
Proposition 4.2. Let G = AB be a weak normal product of A and B, with A and B supersoluble and A normal in G. Then B ʹ is a subnormal subgroup of G.
Proof. Assume the result is not true, and let G be a counterexample of minimal order with ![]() $|A|$ as small as possible. Let p be the largest prime dividing the order of A. Then A has a normal Sylow p-subgroup A p, which is also a normal subgroup of G. Let N be a minimal normal subgroup of G such that
$|A|$ as small as possible. Let p be the largest prime dividing the order of A. Then A has a normal Sylow p-subgroup A p, which is also a normal subgroup of G. Let N be a minimal normal subgroup of G such that ![]() $N \leq A_{p}$. It is clear that
$N \leq A_{p}$. It is clear that ![]() $A_{p}B$ satisfies the hypotheses of the theorem. Assume that
$A_{p}B$ satisfies the hypotheses of the theorem. Assume that ![]() $A_{p}B$ is a proper subgroup of G. By the minimality of G, B ʹ is a subnormal subgroup of
$A_{p}B$ is a proper subgroup of G. By the minimality of G, B ʹ is a subnormal subgroup of ![]() $A_{p}B$. Hence,
$A_{p}B$. Hence, ![]() $B^\prime \leq F(A_{p}B)$. By Lemma 2.1(a),
$B^\prime \leq F(A_{p}B)$. By Lemma 2.1(a), ![]() $G/N$ is a weak normal product of
$G/N$ is a weak normal product of ![]() $A/N$ and
$A/N$ and ![]() $BN/N$. By the minimality of G, we have that
$BN/N$. By the minimality of G, we have that ![]() $B^{\prime}N$ is a subnormal subgroup of G. Since
$B^{\prime}N$ is a subnormal subgroup of G. Since ![]() $N \leq F(A_{p}B)$, it follows that
$N \leq F(A_{p}B)$, it follows that ![]() $B^{\prime}N \leq F(A_{p^\prime}B)$. Hence,
$B^{\prime}N \leq F(A_{p^\prime}B)$. Hence, ![]() $B^{\prime}N$ is a subnormal nilpotent subgroup of G. Consequently,
$B^{\prime}N$ is a subnormal nilpotent subgroup of G. Consequently, ![]() $B^{\prime}N \leq F(G)$. Thus, B ʹ is a subnormal subgroup of G, a contradiction. Hence, we may assume that
$B^{\prime}N \leq F(G)$. Thus, B ʹ is a subnormal subgroup of G, a contradiction. Hence, we may assume that ![]() $G=A_{p}B$. The minimality of
$G=A_{p}B$. The minimality of ![]() $|A|$ implies that
$|A|$ implies that ![]() $A=A_{p}$. Applying now the above Lemma, we conclude that G is supersoluble and therefore Gʹ is nilpotent. Hence, B ʹ is subnormal in G. This final contradiction proves the proposition.
$A=A_{p}$. Applying now the above Lemma, we conclude that G is supersoluble and therefore Gʹ is nilpotent. Hence, B ʹ is subnormal in G. This final contradiction proves the proposition.
Proof of Corollary D
Arguing as in [Reference Monakhov7, Theorem 1], we obtain ![]() $G^{\mathfrak{U}}=(G^\prime)^{\mathfrak{N}}$. Moreover, by [Reference Monakhov7, Lemma 1(3)], we have that
$G^{\mathfrak{U}}=(G^\prime)^{\mathfrak{N}}$. Moreover, by [Reference Monakhov7, Lemma 1(3)], we have that ![]() $G^\prime=A^\prime B^\prime[A,B]=(A^\prime)^{G}(B^\prime)^{G}[A,B]$. Since A is a normal subgroup of G, then A ʹ is a subnormal subgroup of G. Also the application of Proposition 4.2 yields B ʹ is subnormal in G and both A ʹ and B ʹ are nilpotent. Hence,
$G^\prime=A^\prime B^\prime[A,B]=(A^\prime)^{G}(B^\prime)^{G}[A,B]$. Since A is a normal subgroup of G, then A ʹ is a subnormal subgroup of G. Also the application of Proposition 4.2 yields B ʹ is subnormal in G and both A ʹ and B ʹ are nilpotent. Hence, ![]() $(A^\prime)^{G}(B^\prime)^{G}$ is a normal nilpotent subgroup of G. By [Reference Doerk and Hawkes6, II, Lemma II.2.12],
$(A^\prime)^{G}(B^\prime)^{G}$ is a normal nilpotent subgroup of G. By [Reference Doerk and Hawkes6, II, Lemma II.2.12], ![]() $(G^\prime)^{\mathfrak{N}}=((A^\prime)^{G}(B^\prime)^{G})^{\mathfrak{N}}[A,B]^{\mathfrak{N}}=[A,B]^{\mathfrak{N}}$, as desired.
$(G^\prime)^{\mathfrak{N}}=((A^\prime)^{G}(B^\prime)^{G})^{\mathfrak{N}}[A,B]^{\mathfrak{N}}=[A,B]^{\mathfrak{N}}$, as desired.
Acknowledgements
The authors would like to thank the referee for their useful and insightful comments.
Competing interests
The authors declare none.