Hostname: page-component-7479d7b7d-qlrfm Total loading time: 0 Render date: 2024-07-12T22:25:17.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodicity of functionals and representations of normed algebras on reflexive spaces

Published online by Cambridge University Press:  20 January 2009

N. J. Young
N. J. Young
Affiliation:
The University, Glasgow G12 8QW
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is a well-known fact that any normed algebra can be represented isometrically as an algebra of operators with the operator norm. As might be expected from the very universality of this property, it is little used in the study of the structure of an algebra. Far more helpful are representations on Hilbert space, though these are correspondingly hard to come by: isometric representations on Hilbert space are not to be expected in general, and even continuous nontrivial representations may fail to exist. The purpose of this paper is to examine a class of representations intermediate in both availability and utility to those already mentioned—namely, representations on reflexive spaces. There certainly are normed algebras which admit isometric representations of the latter type but have not even faithful representations on Hilbert space: the most natural example is the algebra 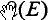of all continuous linear operators on E where E = lp with 1 < p ≠ 2 < ∞, for Berkson and Porta proved in (2) that if E, F are taken from the spaces lp with 1 < p < ∞ and E ≠ F then the only continuous homomorphism from 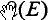into 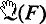is the zero mapping. On the other hand there are also algebras which have no continuous nontrivial representation on any reflexive space—for example the algebra of finite-rank operators on an irreflexive Banach space (see Berkson and Porta (2) or Barnes (1) or Theorem 3, Corollary 1 below).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 20 , Issue 2 , September 1976 , pp. 99 - 120
Copyright
Copyright © Edinburgh Mathematical Society 1976

References

REFERENCES

(1) Barnes, B. A., Representations of normed algebras with minimal left ideals, Proc. Edinburgh Math. Soc. 19 (1974), 173–190.CrossRefGoogle Scholar
(2) Berkson, E. and Porta, H., Representations of ß(X), J. Functional Analysis 3 (1969), 1–34.CrossRefGoogle Scholar
(3) Bonsall, F. F. and Duncan, J., Complete normed algebras (Springer Verlag, Berlin, 1974).Google Scholar
(4) Crvin, P. and Yood, B., The second conjugate space of a Banach algebra as an algebra, Pacific J. Math. 11 (1961), 847–870.Google Scholar
(5) Dixmier, J., Les C*-algèbres et lews représentations (Gauthier-Villars, Paris,1964).Google Scholar
(6) Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires, Mem. Amer. Math. Soc. 16 (1955).Google Scholar
(7) Grothendieck, A., Critères de compacité dans les espaces fonctionnels généraux, Amer. J. Math. 74 (1952), 168–186.CrossRefGoogle Scholar
(8) Halpern, H., Finite sums of irreducible functionals on C*-algebras, Proc. Amer. Math. Soc. 18 (1967), 352–358.Google Scholar
(9) Johnson, B. E., The uniqueness of the (complete) norm topology, Bull. Amer. Math. Soc. 73 (1967), 537–539.CrossRefGoogle Scholar
(10) Pym, J. S., The convolution of functionals on spaces of bounded functions, Proc. London Math. Soc. (3) 15 (1965), 84–104.Google Scholar
(11) Robertson, A. P. and Robertson, W., Topological vector spaces (CambridgeUniversity Press, 1964).Google Scholar
(12) Young, N. J., Separate continuity and multilinear operations, Proc. London Math. Soc. (3) 26 (1973), 289–319.CrossRefGoogle Scholar
(13) Young, N. J., The irregularity of multiplication in group algebras, Quarterly J. Math. (2) 24 (1973), 59–62.CrossRefGoogle Scholar
(14) Davis, W. J., Figiel, T., Johnson, W. B. and Pelczyński, A., Factoring weaklycompact operators, J. Functional Analysis 17 (1974), 311–327.CrossRefGoogle Scholar