Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-07T02:23:20.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Restrictions on meromorphic solutions of Fermat type equations

Part of: Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  08 May 2020

Gary G. Gundersen ,
Katsuya Ishizaki  and
Naofumi Kimura
Gary G. Gundersen
Affiliation:
Department of Mathematics, University of New Orleans, New Orleans, LA70148, USA (ggunders@uno.edu)
Katsuya Ishizaki
Affiliation:
Faculty of Liberal Arts, The Open University of Japan, Wakaba 2-11, Mihama-ku, 261-8586Chiba, Japan (ishizaki@ouj.ac.jp; kim2home2@ma.medias.ne.jp)
Naofumi Kimura
Affiliation:
Faculty of Liberal Arts, The Open University of Japan, Wakaba 2-11, Mihama-ku, 261-8586Chiba, Japan (ishizaki@ouj.ac.jp; kim2home2@ma.medias.ne.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

The Fermat type functional equations 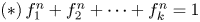$(*)\, f_1^n+f_2^n+\cdots +f_k^n=1$, where n and k are positive integers, are considered in the complex plane. Our focus is on equations of the form (*) where it is not known whether there exist non-constant solutions in one or more of the following four classes of functions: meromorphic functions, rational functions, entire functions, polynomials. For such equations, we obtain estimates on Nevanlinna functions that transcendental solutions of (*) would have to satisfy, as well as analogous estimates for non-constant rational solutions. As an application, it is shown that transcendental entire solutions of (*) when n = k(k − 1) with k ≥ 3, would have to satisfy a certain differential equation, which is a generalization of the known result when k = 3. Alternative proofs for the known non-existence theorems for entire and polynomial solutions of (*) are given. Moreover, some restrictions on degrees of polynomial solutions are discussed.

Keywords

Fermat type functional equationspolynomialsrational functionsmeromorphic functionsentire functionsNevanlinna theorycomplex differential equations

MSC classification

Primary: 30D35: Distribution of values, Nevanlinna theory
Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 654 - 665
Check for updates
Copyright
Copyright © The Authors, 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Gross, F., On the equation f n + g n = 1, Bull. Amer. Math. Soc. 72 (1966), 86–88; Correction Bull. Amer. Math. Soc. 72 (1966), 576.10.1090/S0002-9904-1966-11429-5CrossRefGoogle Scholar
2.Gundersen, G. G., Complex functional equations, in Complex differential and functional equations (Proceedings of the Summer School, Mekrijärvi, 2000). Univ. Joensuu Dept. Math. Rep. Ser. No. 5 (2003), 21–50.Google Scholar
3.Gundersen, G. G., Research questions on meromorphic functions and complex differential equations, Comput. Methods Funct. Theory 17(2) (2017), 195–209.CrossRefGoogle Scholar
4.Gundersen, G. G. and Hayman, W. K., The strength of Cartan's version of Nevanlinna theory, Bull. London Math. Soc. 36 (2004), 433–454.CrossRefGoogle Scholar
5.Hayman, W. K., Meromorphic functions (Clarendon Press, Oxford, 1964).Google Scholar
6.Hayman, W. K., Waring's Problem für analytische Funktionen, Bayer. Akad. Wiss. Math. Natur. kl. Sitzungsber. 1984 (1985), 1–13.Google Scholar
7.Ishizaki, K., A note on the functional equation f n + g n + h n = 1 and some complex differential equations, Comput. Methods Funct. Theory 2 (2002), 67–85.CrossRefGoogle Scholar
8.Ishizaki, K. and Kimura, N., Meromorphic and entire solutions of the functional equation f n + g n + h n = 1 and differential equations, Comput. Methods Funct. Theory 19(1) (2019), 157–172.CrossRefGoogle Scholar
9.Iyer, G., On certain functional equations, J. Indian Math. Soc. 3 (1939), 312–315.Google Scholar
10.Laine, I., Nevanlinna theory and complex differential equations (W. de Gruyter, Berlin, 1993).CrossRefGoogle Scholar
11.Molluzzo, J., Monotonicity of quadrature formulas and polynomial representation, Doctoral thesis (Yeshiva University, 1972).Google Scholar
12.Nevanlinna, R., Analytic functions, translated from the second German edition by Phillip Emig. Grundlehren der Mathematischen Wissenschaften, Volume 162 (Springer-Verlag, Berlin, 1970).Google Scholar
13.Newman, D. J. and Slater, M., Waring's problem for the ring of polynomials, J. Number Theory 11 (1979), 477–487.CrossRefGoogle Scholar
14.Toda, N., On the functional equation $\sum _{i=0}^pa_if^{n_i}_i=1$, Tôhoku Math. J. 23 (1971), 289–299.CrossRefGoogle Scholar