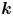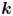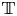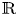Introduction
The field of Laurent series with real coefficients comes with a natural derivation but is too small to be closed under integration and exponentiation. These defects are cured by passing to a certain canonical extension, the ordered differential field $\mathbb {T}$![]() of transseries. Transseries are formal series in an indeterminate $x>\mathbb {R}$
of transseries. Transseries are formal series in an indeterminate $x>\mathbb {R}$![]() , such as
, such as

where $\log ^2 x := (\log x)^2$![]() , etc. Transseries, that is, elements of $\mathbb {T}$
, etc. Transseries, that is, elements of $\mathbb {T}$![]() , are also the logarithmic-exponential series ($\operatorname {LE}$
, are also the logarithmic-exponential series ($\operatorname {LE}$![]() -series, for short) from [Reference van den Dries, Macintyre and Marker4]; we refer to that paper, or to Appendix A of our book [Reference Aschenbrenner, van den Dries and van der Hoeven2], for a detailed construction of $\mathbb {T}$
-series, for short) from [Reference van den Dries, Macintyre and Marker4]; we refer to that paper, or to Appendix A of our book [Reference Aschenbrenner, van den Dries and van der Hoeven2], for a detailed construction of $\mathbb {T}$![]() .
.
What we need for now is that $\mathbb {T}$![]() is a real closed field extension of the field $\mathbb {R}$
is a real closed field extension of the field $\mathbb {R}$![]() of real numbers and that $\mathbb {T}$
of real numbers and that $\mathbb {T}$![]() comes equipped with a distinguished element $x>\mathbb {R}$
comes equipped with a distinguished element $x>\mathbb {R}$![]() , an exponential operation $\exp \colon \mathbb {T} \to \mathbb {T}$
, an exponential operation $\exp \colon \mathbb {T} \to \mathbb {T}$![]() and a distinguished derivation $\partial \colon \mathbb {T}\to \mathbb {T}$
and a distinguished derivation $\partial \colon \mathbb {T}\to \mathbb {T}$![]() . The exponentiation here is an isomorphism of the ordered additive group of $\mathbb {T}$
. The exponentiation here is an isomorphism of the ordered additive group of $\mathbb {T}$![]() onto the ordered multiplicative group $\mathbb {T}^{>}$
onto the ordered multiplicative group $\mathbb {T}^{>}$![]() of positive elements of $\mathbb {T}$
of positive elements of $\mathbb {T}$![]() ; we set $\operatorname {e}^f:=\exp (f)$
; we set $\operatorname {e}^f:=\exp (f)$![]() for $f\in \mathbb {T}$
for $f\in \mathbb {T}$![]() . The derivation $\partial$
. The derivation $\partial$![]() comes from differentiating a transseries termwise with respect to $x$
comes from differentiating a transseries termwise with respect to $x$![]() , and we set $f':= \partial (f)$
, and we set $f':= \partial (f)$![]() , $f'':= \partial ^2(f)$
, $f'':= \partial ^2(f)$![]() , and so on, for $f\in \mathbb {T}$
, and so on, for $f\in \mathbb {T}$![]() ; thus, $x'=1$
; thus, $x'=1$![]() , and $\partial$
, and $\partial$![]() is compatible with exponentiation: $(\operatorname {e}^f)'=f'\operatorname {e}^f$
is compatible with exponentiation: $(\operatorname {e}^f)'=f'\operatorname {e}^f$![]() for $f\in \mathbb {T}$
for $f\in \mathbb {T}$![]() . Moreover, the constant field of $\mathbb {T}$
. Moreover, the constant field of $\mathbb {T}$![]() is $\mathbb {R}$
is $\mathbb {R}$![]() , that is, $\{f\in \mathbb {T}:\,f'=0\}=\mathbb {R}$
, that is, $\{f\in \mathbb {T}:\,f'=0\}=\mathbb {R}$![]() ; see again [Reference Aschenbrenner, van den Dries and van der Hoeven2] for details. Before stating our new results, we introduce some conventions:
; see again [Reference Aschenbrenner, van den Dries and van der Hoeven2] for details. Before stating our new results, we introduce some conventions:
Notations and conventions. Throughout, $m$![]() , $n$
, $n$![]() range over $\mathbb {N}=\{0,\,1,\,2,\,\ldots \}$
range over $\mathbb {N}=\{0,\,1,\,2,\,\ldots \}$![]() . Ordered sets, ordered abelian groups, and ordered fields are totally ordered, by convention. Given an ambient ordered set $S$
. Ordered sets, ordered abelian groups, and ordered fields are totally ordered, by convention. Given an ambient ordered set $S$![]() , a downward closed subset of $S$
, a downward closed subset of $S$![]() , also called a cut in $S$
, also called a cut in $S$![]() , is a set $D\subseteq S$
, is a set $D\subseteq S$![]() such that for all $a,\,b\in S$
such that for all $a,\,b\in S$![]() with $a < b\in D$
with $a < b\in D$![]() we have $a\in D$
we have $a\in D$![]() . For an (additively written) ordered abelian group $\varGamma$
. For an (additively written) ordered abelian group $\varGamma$![]() we set
we set
For any field $K$![]() we let $K^\times =K\setminus \{0\}$
we let $K^\times =K\setminus \{0\}$![]() be its multiplicative group. A differential field is a field $K$
be its multiplicative group. A differential field is a field $K$![]() of characteristic $0$
of characteristic $0$![]() with a derivation $\partial \colon K \to K$
with a derivation $\partial \colon K \to K$![]() , and we set $a':= \partial (a)$
, and we set $a':= \partial (a)$![]() for $a\in K$
for $a\in K$![]() , and let $b^{\dagger} :=b'/b$
, and let $b^{\dagger} :=b'/b$![]() be the logarithmic derivative of $b\in K^\times$
be the logarithmic derivative of $b\in K^\times$![]() when the ambient differential field $K$
when the ambient differential field $K$![]() with its derivation $\partial$
with its derivation $\partial$![]() is clear from the context; note that then $(ab)^{\dagger} =a^{\dagger} + b^{\dagger}$
is clear from the context; note that then $(ab)^{\dagger} =a^{\dagger} + b^{\dagger}$![]() for $a,\,b\in K^\times$
for $a,\,b\in K^\times$![]() .
.
Our book [Reference Aschenbrenner, van den Dries and van der Hoeven2] culminated in an elimination theory for the differential field $\mathbb {T}$![]() of transseries. As a consequence, we found that the induced structure on its constant field $\mathbb {R}$
of transseries. As a consequence, we found that the induced structure on its constant field $\mathbb {R}$![]() is just its semialgebraic structure: if $X\subseteq \mathbb {R}^n$
is just its semialgebraic structure: if $X\subseteq \mathbb {R}^n$![]() is definable in $\mathbb {T}$
is definable in $\mathbb {T}$![]() , then $X$
, then $X$![]() is semialgebraic (in the sense of $\mathbb {R}$
is semialgebraic (in the sense of $\mathbb {R}$![]() ). (Here and throughout “definable in $\mathbf {M}$
). (Here and throughout “definable in $\mathbf {M}$![]() ” means “definable in $\mathbf {M}$
” means “definable in $\mathbf {M}$![]() with parameters from $\mathbf {M}$
with parameters from $\mathbf {M}$![]() ”.)
”.)
The story is more complicated for the structure induced by $\mathbb {T}$![]() on its value group. To explain this, we recall that the natural valuation ring
on its value group. To explain this, we recall that the natural valuation ring
of the real closed field $\mathbb {T}$![]() is clearly $0$
is clearly $0$![]() -definable in $\mathbb {T}$
-definable in $\mathbb {T}$![]() as a differential field, which is how we construe $\mathbb {T}$
as a differential field, which is how we construe $\mathbb {T}$![]() in the rest of this paper. Let $v\colon \mathbb {T}^\times \to \Gamma _{\mathbb {T}}$
in the rest of this paper. Let $v\colon \mathbb {T}^\times \to \Gamma _{\mathbb {T}}$![]() be the corresponding valuation on the field $\mathbb {T}$
be the corresponding valuation on the field $\mathbb {T}$![]() . We may consider $\Gamma _{\mathbb {T}}$
. We may consider $\Gamma _{\mathbb {T}}$![]() as the quotient ${\mathbb {T}^\times }\!/\negmedspace \asymp$
as the quotient ${\mathbb {T}^\times }\!/\negmedspace \asymp$![]() and $v$
and $v$![]() as the natural map to this quotient where $\asymp$
as the natural map to this quotient where $\asymp$![]() is a $0$
is a $0$![]() -definable equivalence relation on $\mathbb {T}^\times$
-definable equivalence relation on $\mathbb {T}^\times$![]() .
.
Thus, $\Gamma _{\mathbb {T}}$![]() is part of $\mathbb {T}^{\operatorname {eq}}$
is part of $\mathbb {T}^{\operatorname {eq}}$![]() . What is the structure induced by $\mathbb {T}$
. What is the structure induced by $\mathbb {T}$![]() on $\Gamma _{\mathbb {T}}$
on $\Gamma _{\mathbb {T}}$![]() ? It includes the structure of $\Gamma _{\mathbb {T}}$
? It includes the structure of $\Gamma _{\mathbb {T}}$![]() as an ordered (by convention, additively written) abelian group. Moreover, the derivation of $\mathbb {T}$
as an ordered (by convention, additively written) abelian group. Moreover, the derivation of $\mathbb {T}$![]() induces a function $\psi \colon \Gamma _{\mathbb {T}}^{\ne } \to \Gamma _{\mathbb {T}}$
induces a function $\psi \colon \Gamma _{\mathbb {T}}^{\ne } \to \Gamma _{\mathbb {T}}$![]() by $\psi (vf)=v(f^{\dagger} )$
by $\psi (vf)=v(f^{\dagger} )$![]() for $f\in \mathbb {T}^\times$
for $f\in \mathbb {T}^\times$![]() with $vf\ne 0$
with $vf\ne 0$![]() . The structure $(\Gamma _{\mathbb {T}},\, \psi )$
. The structure $(\Gamma _{\mathbb {T}},\, \psi )$![]() consisting of the ordered abelian group $\Gamma _{\mathbb {T}}$
consisting of the ordered abelian group $\Gamma _{\mathbb {T}}$![]() with the function $\psi$
with the function $\psi$![]() is the asymptotic couple of $\mathbb {T}$
is the asymptotic couple of $\mathbb {T}$![]() , a notion introduced for differential-valued fields – among which is $\mathbb {T}$
, a notion introduced for differential-valued fields – among which is $\mathbb {T}$![]() —by Rosenlicht [Reference Rosenlicht7]. There is also a natural $0$
—by Rosenlicht [Reference Rosenlicht7]. There is also a natural $0$![]() -definable scalar multiplication
-definable scalar multiplication
that makes $\Gamma _{\mathbb {T}}$![]() into a vector space over $\mathbb {R}$
into a vector space over $\mathbb {R}$![]() ; it is given by $rv(f)=v(f^r)$
; it is given by $rv(f)=v(f^r)$![]() for $f\in \mathbb {T}^{>}$
for $f\in \mathbb {T}^{>}$![]() , and the reason it is $0$
, and the reason it is $0$![]() -definable (in $\mathbb {T}^{\operatorname {eq}}$
-definable (in $\mathbb {T}^{\operatorname {eq}}$![]() ) is that $r\alpha =\beta$
) is that $r\alpha =\beta$![]() (for $r\in \mathbb {R}$
(for $r\in \mathbb {R}$![]() and $\alpha,\, \beta \in \Gamma _{\mathbb {T}}$
and $\alpha,\, \beta \in \Gamma _{\mathbb {T}}$![]() ) iff there are $f,\,g\in \mathbb {T}^{\times }$
) iff there are $f,\,g\in \mathbb {T}^{\times }$![]() such that $\alpha =vf$
such that $\alpha =vf$![]() , $\beta =vg$
, $\beta =vg$![]() and $rf^{\dagger} =g^{\dagger}$
and $rf^{\dagger} =g^{\dagger}$![]() . For this reason, we consider the $2$
. For this reason, we consider the $2$![]() -sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}=((\Gamma _{\mathbb {T}},\,\psi ),\, \mathbb {R}; \operatorname {sc}\!)$
-sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}=((\Gamma _{\mathbb {T}},\,\psi ),\, \mathbb {R}; \operatorname {sc}\!)$![]() consisting of the asymptotic couple $(\Gamma _{\mathbb {T}},\,\psi )$
consisting of the asymptotic couple $(\Gamma _{\mathbb {T}},\,\psi )$![]() , the field $\mathbb {R}$
, the field $\mathbb {R}$![]() , and the above scalar multiplication
, and the above scalar multiplication
The basic elementary properties of this $2$![]() -sorted structure were determined in [Reference Aschenbrenner and van den Dries1]. This structure encodes important features of $\mathbb {T}$
-sorted structure were determined in [Reference Aschenbrenner and van den Dries1]. This structure encodes important features of $\mathbb {T}$![]() , and in this paper, we prove a new result about it in § 5:
, and in this paper, we prove a new result about it in § 5:
Theorem 0.1 Let $\Gamma _{\mathbb {T}}$![]() be equipped with its order topology, and let $X\subseteq \Gamma _{\mathbb {T}}$
be equipped with its order topology, and let $X\subseteq \Gamma _{\mathbb {T}}$![]() be definable in $\boldsymbol {\Gamma }_{\mathbb {T}}$
be definable in $\boldsymbol {\Gamma }_{\mathbb {T}}$![]() . Then the following are equivalent:
. Then the following are equivalent:
(i) $X$
 is contained in a finite-dimensional $\mathbb {R}$
is contained in a finite-dimensional $\mathbb {R}$ -linear subspace of $\Gamma _{\mathbb {T}};$
-linear subspace of $\Gamma _{\mathbb {T}};$
(ii) $X$
 is discrete;
is discrete;(iii) $X$
 has an empty interior in $\Gamma _{\mathbb {T}}$
has an empty interior in $\Gamma _{\mathbb {T}}$ .
.
We also know from [Reference Aschenbrenner, van den Dries and van der Hoeven2, Corollaries 14.3.10, 14.3.11] that for any non-zero differential polynomial $G(Y)\in \mathbb {T}\{Y\}$![]() the subset $\big \{vy:\,y\in \mathbb {T}^\times,\,\ G(y)=0\big \}$
the subset $\big \{vy:\,y\in \mathbb {T}^\times,\,\ G(y)=0\big \}$![]() of $\Gamma _{\mathbb {T}}$
of $\Gamma _{\mathbb {T}}$![]() is discrete. The set of zeros of
is discrete. The set of zeros of
in $\mathbb {T}$![]() is
is
For this $G$![]() the set $\big \{vy:\,y\in \mathbb {T}^\times,\,\ G(y)=0\big \}$
the set $\big \{vy:\,y\in \mathbb {T}^\times,\,\ G(y)=0\big \}$![]() is not contained in a finite-dimensional $\mathbb {R}$
is not contained in a finite-dimensional $\mathbb {R}$![]() -linear subspace of $\Gamma _{\mathbb {T}}$
-linear subspace of $\Gamma _{\mathbb {T}}$![]() and thus not definable in the $2$
and thus not definable in the $2$![]() -sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}$
-sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}$![]() by the theorem above. We treat this example in more detail at the end of § 1.
by the theorem above. We treat this example in more detail at the end of § 1.
The authors of [Reference Aschenbrenner and van den Dries1] had speculated that the subsets of $\Gamma _{\mathbb {T}}$![]() definable in $\mathbb {T}^{\operatorname {eq}}$
definable in $\mathbb {T}^{\operatorname {eq}}$![]() might be just those that are definable in the $2$
might be just those that are definable in the $2$![]() -sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}$
-sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}$![]() . The above is a counter example but leaves open the possibility that $\Gamma _{\mathbb {T}}$
. The above is a counter example but leaves open the possibility that $\Gamma _{\mathbb {T}}$![]() is stably embedded in $\mathbb {T}^{\operatorname {eq}}$
is stably embedded in $\mathbb {T}^{\operatorname {eq}}$![]() . In this connection, we note that for all intents and purposes, we can replace the $2$
. In this connection, we note that for all intents and purposes, we can replace the $2$![]() -sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}$
-sorted structure $\boldsymbol {\Gamma }_{\mathbb {T}}$![]() by the $1$
by the $1$![]() -sorted structure $(\Gamma _{\mathbb {T}};\psi,\,\mathbb {R} 1,\,\operatorname {sc})$
-sorted structure $(\Gamma _{\mathbb {T}};\psi,\,\mathbb {R} 1,\,\operatorname {sc})$![]() consisting of the asymptotic couple $(\Gamma _{\mathbb {T}}; \psi )$
consisting of the asymptotic couple $(\Gamma _{\mathbb {T}}; \psi )$![]() expanded by the set $\mathbb {R} 1\subseteq \Gamma _{\mathbb {T}}$
expanded by the set $\mathbb {R} 1\subseteq \Gamma _{\mathbb {T}}$![]() , where $1=v(x^{-1})\in \Gamma _{\mathbb {T}}^{>}$
, where $1=v(x^{-1})\in \Gamma _{\mathbb {T}}^{>}$![]() is the unique fixed point of $\psi$
is the unique fixed point of $\psi$![]() , and by the function
, and by the function
Why revisit closed asymptotic couples?
The proof of Theorem 0.1 requires the results of [Reference Aschenbrenner and van den Dries1], suitably extended. This was our original motive for revisiting the subject of closed asymptotic couples. The theorem itself is of interest but is also needed for its application to the induced structure on the value group of $\mathbb {T}$![]() .
.
The quantifier elimination (QE) for closed asymptotic couples in [Reference Aschenbrenner and van den Dries1] was expected to help in obtaining a QE for $\mathbb {T}$![]() . The latter is achieved in [Reference Aschenbrenner, van den Dries and van der Hoeven2, Chapter 16], but there we needed only a key lemma from [Reference Aschenbrenner and van den Dries1], not its QE for closed asymptotic couples. That key lemma is [Reference Aschenbrenner and van den Dries1, Property B], and is given a self-contained proof of five dense pages in [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.9]. Since then, we found a simpler way to obtain the QE in [Reference Aschenbrenner and van den Dries1] that does not use the key lemma alluded to but depends on some easier-to-prove new lemmas that have also other applications; see § 2. This new proof of QE, given in § 3, is another reason for revisiting the subject of closed asymptotic couples. (We derive the “key lemma” itself as a routine consequence of the QE for closed asymptotic couples: Proposition 6.3.)
. The latter is achieved in [Reference Aschenbrenner, van den Dries and van der Hoeven2, Chapter 16], but there we needed only a key lemma from [Reference Aschenbrenner and van den Dries1], not its QE for closed asymptotic couples. That key lemma is [Reference Aschenbrenner and van den Dries1, Property B], and is given a self-contained proof of five dense pages in [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.9]. Since then, we found a simpler way to obtain the QE in [Reference Aschenbrenner and van den Dries1] that does not use the key lemma alluded to but depends on some easier-to-prove new lemmas that have also other applications; see § 2. This new proof of QE, given in § 3, is another reason for revisiting the subject of closed asymptotic couples. (We derive the “key lemma” itself as a routine consequence of the QE for closed asymptotic couples: Proposition 6.3.)
For his study of transexponential pre-$H$![]() -fields in [Reference Pynn-Coates6, Chapter 6] and [Reference Pynn-Coates5], Nigel Pynn-Coates introduced a modified version of “closed asymptotic couple” and adapted accordingly some material from our (unpublished) 2017 version of this paper. Getting the paper published is also more urgent now because in our recent proof that maximal Hardy fields are $\eta _1$
-fields in [Reference Pynn-Coates6, Chapter 6] and [Reference Pynn-Coates5], Nigel Pynn-Coates introduced a modified version of “closed asymptotic couple” and adapted accordingly some material from our (unpublished) 2017 version of this paper. Getting the paper published is also more urgent now because in our recent proof that maximal Hardy fields are $\eta _1$![]() we use results from § 4 below.
we use results from § 4 below.
Finally, this paper gives us an opportunity to enhance and better organize parts of [Reference Aschenbrenner and van den Dries1], and acknowledge gaps in some proofs there; we intend to close these gaps in a follow-up to the present paper. No familiarity with [Reference Aschenbrenner and van den Dries1] is needed, but we do assume as background some 20 pages (mainly on asymptotic couples) from [Reference Aschenbrenner, van den Dries and van der Hoeven2], namely parts of § 2.4 on ordered abelian groups, Sections 6.5, 9.1 (subsection on asymptotic couples), 9.2 (first four pages), and 9.8. For the reader's convenience, we also repeat definitions of key notions concerning asymptotic couples and $H$![]() -fields.
-fields.
We thank Nigel Pynn-Coates for his careful reading of this paper, and corrections, and the referee for helpful comments.
1. Preliminaries
We only consider asymptotic couples of $H$![]() -type, calling them $H$
-type, calling them $H$![]() -couples for brevity. Thus, an $H$
-couples for brevity. Thus, an $H$![]() -couple is a pair $(\Gamma,\,\psi )$
-couple is a pair $(\Gamma,\,\psi )$![]() consisting of an ordered abelian group $\Gamma$
consisting of an ordered abelian group $\Gamma$![]() with a map $\psi \colon \Gamma ^{\ne }\to \Gamma$
with a map $\psi \colon \Gamma ^{\ne }\to \Gamma$![]() , such that for all $\alpha,\,\beta \in \Gamma ^{\ne }$
, such that for all $\alpha,\,\beta \in \Gamma ^{\ne }$![]() ,
,
(AC1) $\alpha +\beta \ne 0\ \Longrightarrow \ \psi (\alpha +\beta )\geqslant \min \!(\psi (\alpha ),\,\psi (\beta ))$
 ;
;(AC2) $\psi (k\alpha )=\psi (\alpha )$
 for all $k\in \mathbb {Z}^{\ne }$
for all $k\in \mathbb {Z}^{\ne }$ ;
;(AC3) $\alpha >0\ \Longrightarrow \alpha +\psi (\alpha )> \psi (\beta )$
 ;
;(HC) $0<\alpha \leqslant \beta \ \Longrightarrow \ \psi (\alpha )\geqslant \psi (\beta )$
 .
.
(As an aside, note that (AC2) and (HC) together imply (AC1); had we observed this earlier, it would have shortened some arguments in [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.8]; the reader can use it to the same effect in § 2 of the present paper.) Let $(\Gamma,\,\psi )$![]() be an $H$
be an $H$![]() -couple. By (AC1) and (AC2) the function $\psi$
-couple. By (AC1) and (AC2) the function $\psi$![]() is a valuation on the abelian group $\Gamma$
is a valuation on the abelian group $\Gamma$![]() ; as usual, we extend $\psi$
; as usual, we extend $\psi$![]() to $\psi \colon \Gamma \to \Gamma _{\infty }:=\Gamma \cup \{\infty \}$
to $\psi \colon \Gamma \to \Gamma _{\infty }:=\Gamma \cup \{\infty \}$![]() by $\psi (0):= \infty$
by $\psi (0):= \infty$![]() ; we use $\alpha ^{\dagger}$
; we use $\alpha ^{\dagger}$![]() as an alternative notation for $\psi (\alpha )$
as an alternative notation for $\psi (\alpha )$![]() and set $\alpha ':=\alpha +\alpha ^{\dagger}$
and set $\alpha ':=\alpha +\alpha ^{\dagger}$![]() for $\alpha \in \Gamma$
for $\alpha \in \Gamma$![]() . Also $\Psi := \psi (\Gamma ^{\ne })$
. Also $\Psi := \psi (\Gamma ^{\ne })$![]() . We recall from [Reference Aschenbrenner, van den Dries and van der Hoeven2, Corollary 9.2.16] a basic trichotomy for $H$
. We recall from [Reference Aschenbrenner, van den Dries and van der Hoeven2, Corollary 9.2.16] a basic trichotomy for $H$![]() -couples which says that we are in exactly one of the following three cases:
-couples which says that we are in exactly one of the following three cases:
• $(\Gamma,\,\psi )$
 has a (necessarily unique) gap, that is, an element $\gamma \in \Gamma$
has a (necessarily unique) gap, that is, an element $\gamma \in \Gamma$ such that $\Psi < \gamma < (\Gamma ^{>})'$
such that $\Psi < \gamma < (\Gamma ^{>})'$ ;
;• $(\Gamma,\,\psi )$
 is grounded, that is, $\Psi$
is grounded, that is, $\Psi$ has a largest element;
has a largest element;• $(\Gamma,\,\psi )$
 has asymptotic integration, that is, $\Gamma =(\Gamma ^{\ne })'$
has asymptotic integration, that is, $\Gamma =(\Gamma ^{\ne })'$ .
.
We say that $(\Gamma,\,\psi )$![]() is closed if $\Gamma$
is closed if $\Gamma$![]() is divisible, $\Psi \subseteq \Gamma$
is divisible, $\Psi \subseteq \Gamma$![]() is downward closed, and $(\Gamma,\,\psi )$
is downward closed, and $(\Gamma,\,\psi )$![]() has asymptotic integration. We also use the qualifiers having a gap, grounded, having asymptotic integration, and closed for $H$
has asymptotic integration. We also use the qualifiers having a gap, grounded, having asymptotic integration, and closed for $H$![]() -couples with extra structure.
-couples with extra structure.
An $H$![]() -cut in $(\Gamma,\,\psi )$
-cut in $(\Gamma,\,\psi )$![]() is a downward closed set $P\subseteq \Gamma$
is a downward closed set $P\subseteq \Gamma$![]() such that $\Psi \subseteq P<(\Gamma ^{>})'$
such that $\Psi \subseteq P<(\Gamma ^{>})'$![]() . The set $\Psi ^{\downarrow }:=\{\alpha \in \Gamma :\, \alpha \leqslant \beta for some \beta \in \Psi \}$
. The set $\Psi ^{\downarrow }:=\{\alpha \in \Gamma :\, \alpha \leqslant \beta for some \beta \in \Psi \}$![]() is an $H$
is an $H$![]() -cut in $(\Gamma,\,\psi )$
-cut in $(\Gamma,\,\psi )$![]() , and if $(\Gamma,\,\psi )$
, and if $(\Gamma,\,\psi )$![]() is grounded or has asymptotic integration, this is the only $H$
is grounded or has asymptotic integration, this is the only $H$![]() -cut in $(\Gamma,\,\psi )$
-cut in $(\Gamma,\,\psi )$![]() . If $(\Gamma,\,\psi )$
. If $(\Gamma,\,\psi )$![]() has a gap $\beta$
has a gap $\beta$![]() , then $\Psi ^{\downarrow }\cup \{\beta \}$
, then $\Psi ^{\downarrow }\cup \{\beta \}$![]() is the only other $H$
is the only other $H$![]() -cut in $(\Gamma,\,\psi )$
-cut in $(\Gamma,\,\psi )$![]() .
.
In particular, if $(\Gamma,\,\psi )$![]() is closed, then $\Psi$
is closed, then $\Psi$![]() is the only $H$
is the only $H$![]() -cut in $(\Gamma,\,\psi )$
-cut in $(\Gamma,\,\psi )$![]() , but in eliminating quantifiers for closed $H$
, but in eliminating quantifiers for closed $H$![]() -couples in § 3, it is essential to have a predicate for this $H$
-couples in § 3, it is essential to have a predicate for this $H$![]() -cut in our language.
-cut in our language.
Where do closed $H$ -couples come from?
-couples come from?
We recall from [Reference Aschenbrenner, van den Dries and van der Hoeven2, Chapter 10] that an $H$![]() -field is an ordered differential field $K$
-field is an ordered differential field $K$![]() with constant field $C$
with constant field $C$![]() such that:
such that:
(H1) $a'>0$
 for all $a\in K$
for all $a\in K$ with $a>C$
with $a>C$ ;
;(H2) $\mathcal {O}=C+ o$
 , where $\mathcal {O}$
, where $\mathcal {O}$ is the convex hull of $C$
is the convex hull of $C$ in the ordered field $K$
in the ordered field $K$ , and $ o$
, and $ o$ is the maximal ideal of the valuation ring $\mathcal {O}$
is the maximal ideal of the valuation ring $\mathcal {O}$ .
.
Let $K$![]() be an $H$
be an $H$![]() -field, and let $\mathcal {O}$
-field, and let $\mathcal {O}$![]() and $o$
and $o$![]() be as in (H2). Thus, $K$
be as in (H2). Thus, $K$![]() is a valued field with valuation ring $\mathcal {O}$
is a valued field with valuation ring $\mathcal {O}$![]() . Let $v\colon K^\times \to \Gamma$
. Let $v\colon K^\times \to \Gamma$![]() be the associated valuation. The value group $\Gamma =v(K^\times )$
be the associated valuation. The value group $\Gamma =v(K^\times )$![]() is made into an $H$
is made into an $H$![]() -couple $(\Gamma,\,\psi )$
-couple $(\Gamma,\,\psi )$![]() —the $H$
—the $H$![]() -couple of $K$
-couple of $K$![]() —by $\psi (vf):=v(f^{\dagger} )$
—by $\psi (vf):=v(f^{\dagger} )$![]() for $f\in K^\times$
for $f\in K^\times$![]() with $vf\ne 0$
with $vf\ne 0$![]() . We call $K$
. We call $K$![]() Liouville closed if it is real closed and for all $a\in K$
Liouville closed if it is real closed and for all $a\in K$![]() there exists $b\in K$
there exists $b\in K$![]() with $a=b'$
with $a=b'$![]() and also a $b\in K^\times$
and also a $b\in K^\times$![]() such that $a=b^{\dagger}$
such that $a=b^{\dagger}$![]() .
.
If $K$![]() is Liouville closed, its $H$
is Liouville closed, its $H$![]() -couple is closed as is easily verified. We recall from [Reference Aschenbrenner, van den Dries and van der Hoeven2] that $\mathbb {T}$
-couple is closed as is easily verified. We recall from [Reference Aschenbrenner, van den Dries and van der Hoeven2] that $\mathbb {T}$![]() is a Liouville closed $H$
is a Liouville closed $H$![]() -field.
-field.
Ordered vector spaces
Throughout we let ${\boldsymbol {k}}$![]() , ${\boldsymbol {k}}_0$
, ${\boldsymbol {k}}_0$![]() , and ${\boldsymbol {k}}^*$
, and ${\boldsymbol {k}}^*$![]() be ordered fields. Recall that an ordered vector space over ${\boldsymbol {k}}$
be ordered fields. Recall that an ordered vector space over ${\boldsymbol {k}}$![]() is an ordered abelian group $\Gamma$
is an ordered abelian group $\Gamma$![]() with a scalar multiplication ${\boldsymbol {k}}\times \Gamma \to \Gamma$
with a scalar multiplication ${\boldsymbol {k}}\times \Gamma \to \Gamma$![]() that makes $\Gamma$
that makes $\Gamma$![]() into a vector space over ${\boldsymbol {k}}$
into a vector space over ${\boldsymbol {k}}$![]() such that $c\gamma >0$
such that $c\gamma >0$![]() for all $c\in {\boldsymbol {k}}^{>}$
for all $c\in {\boldsymbol {k}}^{>}$![]() and $\gamma \in \Gamma ^{>}$
and $\gamma \in \Gamma ^{>}$![]() . Let $\Gamma$
. Let $\Gamma$![]() be an ordered vector space over ${\boldsymbol {k}}$
be an ordered vector space over ${\boldsymbol {k}}$![]() . Then any ${\boldsymbol {k}}$
. Then any ${\boldsymbol {k}}$![]() -linear subspace of $\Gamma$
-linear subspace of $\Gamma$![]() is considered as an ordered vector space over ${\boldsymbol {k}}$
is considered as an ordered vector space over ${\boldsymbol {k}}$![]() in the obvious way. We shall need the following easy result about $\Gamma$
in the obvious way. We shall need the following easy result about $\Gamma$![]() :
:
Lemma 1.1 Let $\Gamma _0$![]() be a ${\boldsymbol {k}}$
be a ${\boldsymbol {k}}$![]() -linear subspace of $\Gamma$
-linear subspace of $\Gamma$![]() . Suppose $\Gamma$
. Suppose $\Gamma$![]() contains an element $\varepsilon$
contains an element $\varepsilon$![]() with $0 < \varepsilon < \Gamma _0^{>}$
with $0 < \varepsilon < \Gamma _0^{>}$![]() . Then $\Gamma _0$
. Then $\Gamma _0$![]() is closed in $\Gamma$
is closed in $\Gamma$![]() with respect to the order topology on $\Gamma$
with respect to the order topology on $\Gamma$![]() .
.
Proof. Let $\gamma \in \Gamma \setminus \Gamma _0$![]() . With $\varepsilon$
. With $\varepsilon$![]() as in the hypothesis, we observe that the interval ${(\gamma -\varepsilon,\, \gamma +\varepsilon )}$
as in the hypothesis, we observe that the interval ${(\gamma -\varepsilon,\, \gamma +\varepsilon )}$![]() can have at most one point in it from $\Gamma _0$
can have at most one point in it from $\Gamma _0$![]() , and so by decreasing $\varepsilon$
, and so by decreasing $\varepsilon$![]() we can arrange that $(\gamma -\varepsilon,\, \gamma +\varepsilon )\cap \Gamma _0=\emptyset$
we can arrange that $(\gamma -\varepsilon,\, \gamma +\varepsilon )\cap \Gamma _0=\emptyset$![]() .
.
The ${\boldsymbol {k}}$![]() -archimedean class of $\alpha \in \Gamma$
-archimedean class of $\alpha \in \Gamma$![]() is
is
Let $[\Gamma ]_{{\boldsymbol {k}}}$![]() be the set of ${\boldsymbol {k}}$
be the set of ${\boldsymbol {k}}$![]() -archimedean classes. Then $[\Gamma ]_{{\boldsymbol {k}}}$
-archimedean classes. Then $[\Gamma ]_{{\boldsymbol {k}}}$![]() is a partition of $\Gamma$
is a partition of $\Gamma$![]() , and we linearly order $[\Gamma ]_{{\boldsymbol {k}}}$
, and we linearly order $[\Gamma ]_{{\boldsymbol {k}}}$![]() by
by
Thus, $[0]_{{\boldsymbol {k}}}=\{0\}$![]() is the smallest ${\boldsymbol {k}}$
is the smallest ${\boldsymbol {k}}$![]() -archimedean class. For $\alpha,\,\beta \in \Gamma$
-archimedean class. For $\alpha,\,\beta \in \Gamma$![]() , $c\in {\boldsymbol {k}}^\times$
, $c\in {\boldsymbol {k}}^\times$![]() we have $[c\alpha ]_{{\boldsymbol {k}}}=[\alpha ]_{{\boldsymbol {k}}}$
we have $[c\alpha ]_{{\boldsymbol {k}}}=[\alpha ]_{{\boldsymbol {k}}}$![]() and $[\alpha +\beta ]_{{\boldsymbol {k}}} \leqslant \max ([\alpha ]_{{\boldsymbol {k}}},\,[\beta ]_{{\boldsymbol {k}}})$
and $[\alpha +\beta ]_{{\boldsymbol {k}}} \leqslant \max ([\alpha ]_{{\boldsymbol {k}}},\,[\beta ]_{{\boldsymbol {k}}})$![]() , with equality if $[\alpha ]_{{\boldsymbol {k}}}\neq [\beta ]_{{\boldsymbol {k}}}$
, with equality if $[\alpha ]_{{\boldsymbol {k}}}\neq [\beta ]_{{\boldsymbol {k}}}$![]() .
.
Lemma 1.2 Let $\Gamma \ne \{0\}$![]() be an ordered vector space over ${\boldsymbol {k}}$
be an ordered vector space over ${\boldsymbol {k}}$![]() such that $[\Gamma ^{\ne }]_{{\boldsymbol {k}}}$
such that $[\Gamma ^{\ne }]_{{\boldsymbol {k}}}$![]() has no least element. Then every finite-dimensional ${\boldsymbol {k}}$
has no least element. Then every finite-dimensional ${\boldsymbol {k}}$![]() -linear subspace of $\Gamma$
-linear subspace of $\Gamma$![]() is discrete with respect to the order topology on $\Gamma$
is discrete with respect to the order topology on $\Gamma$![]() .
.
Proof. First note that if $\gamma _1,\,\ldots,\,\gamma _n\in \Gamma ^{\ne }$![]() and $[\gamma _1]_{{\boldsymbol {k}}},\,\ldots,\,[\gamma _n]_{{\boldsymbol {k}}}$
and $[\gamma _1]_{{\boldsymbol {k}}},\,\ldots,\,[\gamma _n]_{{\boldsymbol {k}}}$![]() are distinct, then $\gamma _1,\,\ldots,\,\gamma _n$
are distinct, then $\gamma _1,\,\ldots,\,\gamma _n$![]() are ${\boldsymbol {k}}$
are ${\boldsymbol {k}}$![]() -linearly independent. Thus, for a finite-dimensional ${\boldsymbol {k}}$
-linearly independent. Thus, for a finite-dimensional ${\boldsymbol {k}}$![]() -linear subspace $\Delta \ne \{0\}$
-linear subspace $\Delta \ne \{0\}$![]() of $\Gamma$
of $\Gamma$![]() we can take $\delta \in \Delta ^{\ne }$
we can take $\delta \in \Delta ^{\ne }$![]() such that $[\delta ]_{{\boldsymbol {k}}}$
such that $[\delta ]_{{\boldsymbol {k}}}$![]() is minimal in $[\Delta ^{\ne }]_{{\boldsymbol {k}}}$
is minimal in $[\Delta ^{\ne }]_{{\boldsymbol {k}}}$![]() . Then for any $\alpha \in \Delta$
. Then for any $\alpha \in \Delta$![]() and $\beta \in \Gamma ^{\ne }$
and $\beta \in \Gamma ^{\ne }$![]() with $[\beta ]_{{\boldsymbol {k}}}<[\delta ]_{{\boldsymbol {k}}}$
with $[\beta ]_{{\boldsymbol {k}}}<[\delta ]_{{\boldsymbol {k}}}$![]() we have $\alpha +\beta \notin \Delta$
we have $\alpha +\beta \notin \Delta$![]() .
.
Lemma 1.2 takes care of the easy direction (i) $\Rightarrow$![]() (ii) in Theorem 0.1. The direction (ii) $\Rightarrow$
(ii) in Theorem 0.1. The direction (ii) $\Rightarrow$![]() (iii) is trivial. The harder direction (iii) $\Rightarrow$
(iii) is trivial. The harder direction (iii) $\Rightarrow$![]() (i) uses a generality on expanded vector spaces, to which we now turn.
(i) uses a generality on expanded vector spaces, to which we now turn.
Let $V$![]() be a vector space over a field $C$
be a vector space over a field $C$![]() . We consider the two-sorted structure $(V,\,C;\operatorname {sc})$
. We consider the two-sorted structure $(V,\,C;\operatorname {sc})$![]() consisting of the abelian group $V$
consisting of the abelian group $V$![]() , the field $C$
, the field $C$![]() , and the scalar multiplication $\operatorname {sc}\colon C\times V \to V$
, and the scalar multiplication $\operatorname {sc}\colon C\times V \to V$![]() of the vector space $V$
of the vector space $V$![]() . Let $X\subseteq V$
. Let $X\subseteq V$![]() . Then we have the expansion $\mathbf {V}=((V,\,X),\,C;\operatorname {sc}\!)$
. Then we have the expansion $\mathbf {V}=((V,\,X),\,C;\operatorname {sc}\!)$![]() of $(V,\,C;\operatorname {sc})$
of $(V,\,C;\operatorname {sc})$![]() . Let $\mathbf {V}^*=((V^*,\, X^*),\, C^*;\operatorname {sc}\!)$
. Let $\mathbf {V}^*=((V^*,\, X^*),\, C^*;\operatorname {sc}\!)$![]() be an elementary extension of $\mathbf {V}$
be an elementary extension of $\mathbf {V}$![]() . Let $C^* V$
. Let $C^* V$![]() be the $C^*$
be the $C^*$![]() -linear subspace of $V^*$
-linear subspace of $V^*$![]() spanned by $V$
spanned by $V$![]() .
.
Lemma 1.3 Assume $\mathbf {V}^*$![]() is $|V|^+$
is $|V|^+$![]() -saturated. Then $X$
-saturated. Then $X$![]() is contained in a finite-dimensional $C$
is contained in a finite-dimensional $C$![]() -linear subspace of $V$
-linear subspace of $V$![]() if and only if $X^*\subseteq C^*V$
if and only if $X^*\subseteq C^*V$![]() .
.
Proof. If $X\subseteq Cv_1+\cdots + Cv_n$![]() , $v_1,\,\ldots,\, v_n\in V$
, $v_1,\,\ldots,\, v_n\in V$![]() , then $X^*\subseteq C^*v_1+\cdots + C^*v_n\subseteq C^*V$
, then $X^*\subseteq C^*v_1+\cdots + C^*v_n\subseteq C^*V$![]() . We prove the contrapositive of the other direction, so assume $X\not \subseteq Cv_1+\cdots +Cv_n$
. We prove the contrapositive of the other direction, so assume $X\not \subseteq Cv_1+\cdots +Cv_n$![]() for all $v_1,\,\ldots,\, v_n\in V$
for all $v_1,\,\ldots,\, v_n\in V$![]() . Then $X^*\not \subseteq C^*v_1+\cdots +C^*v_n$
. Then $X^*\not \subseteq C^*v_1+\cdots +C^*v_n$![]() for all $v_1,\,\ldots,\, v_n\in V$
for all $v_1,\,\ldots,\, v_n\in V$![]() , and so by saturation we get an element of $X^*$
, and so by saturation we get an element of $X^*$![]() that does not lie in $C^*V$
that does not lie in $C^*V$![]() .
.
For certain $(V,\,C;\operatorname {sc})$![]() this will be applied to sets $X\subseteq V$
this will be applied to sets $X\subseteq V$![]() that are definable in a suitable expansion of $(V,\,C;\operatorname {sc})$
that are definable in a suitable expansion of $(V,\,C;\operatorname {sc})$![]() , with $X^*$
, with $X^*$![]() the corresponding set in an elementary extension of that expansion.
the corresponding set in an elementary extension of that expansion.
$H$ -couples over ordered fields
-couples over ordered fields
Ordered vector spaces come into play as follows. Let $K$![]() be a Liouville closed $H$
be a Liouville closed $H$![]() -field. It has the (ordered) constant field $C$
-field. It has the (ordered) constant field $C$![]() , and the $H$
, and the $H$![]() -couple $(\Gamma,\,\psi )$
-couple $(\Gamma,\,\psi )$![]() . We have a map $(c,\,\gamma )\mapsto c\gamma \colon C\times \Gamma \to \Gamma$
. We have a map $(c,\,\gamma )\mapsto c\gamma \colon C\times \Gamma \to \Gamma$![]() such that $cvf=vg$
such that $cvf=vg$![]() whenever $f,\,g\in K^\times$
whenever $f,\,g\in K^\times$![]() and $cf^{\dagger} =g^{\dagger}$
and $cf^{\dagger} =g^{\dagger}$![]() . This map makes $\Gamma$
. This map makes $\Gamma$![]() into an ordered vector space over $C$
into an ordered vector space over $C$![]() , and $\psi (c\gamma )=\psi (\gamma )$
, and $\psi (c\gamma )=\psi (\gamma )$![]() for all $c\in C^\times$
for all $c\in C^\times$![]() and $\gamma \in \Gamma ^{\ne }$
and $\gamma \in \Gamma ^{\ne }$![]() .
.
Accordingly, we define an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() to be an $H$
to be an $H$![]() -couple $(\Gamma,\,\psi )$
-couple $(\Gamma,\,\psi )$![]() where the ordered abelian group $\Gamma$
where the ordered abelian group $\Gamma$![]() is also equipped with a map ${\boldsymbol {k}}\times \Gamma \to \Gamma$
is also equipped with a map ${\boldsymbol {k}}\times \Gamma \to \Gamma$![]() making $\Gamma$
making $\Gamma$![]() into an ordered vector space over ${\boldsymbol {k}}$
into an ordered vector space over ${\boldsymbol {k}}$![]() such that $\psi (c\gamma )=\psi (\gamma )$
such that $\psi (c\gamma )=\psi (\gamma )$![]() for all $c\in {\boldsymbol {k}}^\times$
for all $c\in {\boldsymbol {k}}^\times$![]() and $\gamma \in \Gamma ^{\ne }$
and $\gamma \in \Gamma ^{\ne }$![]() . Thus, the $H$
. Thus, the $H$![]() -couple of a Liouville closed $H$
-couple of a Liouville closed $H$![]() -field is naturally an $H$
-field is naturally an $H$![]() -couple over its constant field.
-couple over its constant field.
Let $(\Gamma,\,\psi )$![]() be an $H$
be an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() . A basic fact is that for distinct $\alpha,\,\beta \in \Gamma ^{\ne }$
. A basic fact is that for distinct $\alpha,\,\beta \in \Gamma ^{\ne }$![]() we have $[\psi (\alpha )-\psi (\beta )]_{{\boldsymbol {k}}} < [\alpha -\beta ]_{{\boldsymbol {k}}}$
we have $[\psi (\alpha )-\psi (\beta )]_{{\boldsymbol {k}}} < [\alpha -\beta ]_{{\boldsymbol {k}}}$![]() , since for all $c\in {\boldsymbol {k}}^{>}$
, since for all $c\in {\boldsymbol {k}}^{>}$![]() , we have $\psi (\alpha )-\psi (\beta )=\psi (c\alpha )-\psi (c\beta )=o(c(\alpha -\beta ))$
, we have $\psi (\alpha )-\psi (\beta )=\psi (c\alpha )-\psi (c\beta )=o(c(\alpha -\beta ))$![]() , by [Reference Aschenbrenner, van den Dries and van der Hoeven2, 6.5.4(ii)]. Note also that for all $\alpha,\,\beta \in \Gamma ^{\ne }$
, by [Reference Aschenbrenner, van den Dries and van der Hoeven2, 6.5.4(ii)]. Note also that for all $\alpha,\,\beta \in \Gamma ^{\ne }$![]() ,
,
Hahn spaces
These are the ordered Hahn spaces from [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 2.4]: a Hahn space $\Gamma$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() is an ordered vector space over ${\boldsymbol {k}}$
is an ordered vector space over ${\boldsymbol {k}}$![]() such that for all $\alpha,\,\beta \in \Gamma ^{\neq }$
such that for all $\alpha,\,\beta \in \Gamma ^{\neq }$![]() with $[\alpha ]_{{\boldsymbol {k}}}=[\beta ]_{{\boldsymbol {k}}}$
with $[\alpha ]_{{\boldsymbol {k}}}=[\beta ]_{{\boldsymbol {k}}}$![]() there exists $c\in {\boldsymbol {k}}^\times$
there exists $c\in {\boldsymbol {k}}^\times$![]() such that $[\alpha -c\beta ]_{{\boldsymbol {k}}}<[\alpha ]_{{\boldsymbol {k}}}$
such that $[\alpha -c\beta ]_{{\boldsymbol {k}}}<[\alpha ]_{{\boldsymbol {k}}}$![]() .
.
Examples
(1) Any one-dimensional ordered vector space over ${\boldsymbol {k}}$
 is a Hahn space over ${\boldsymbol {k}}$
is a Hahn space over ${\boldsymbol {k}}$ .
.(2) Any ${\boldsymbol {k}}$
 -linear subspace of a Hahn space over ${\boldsymbol {k}}$
-linear subspace of a Hahn space over ${\boldsymbol {k}}$ is a Hahn space over ${\boldsymbol {k}}$
is a Hahn space over ${\boldsymbol {k}}$ .
.(3) Any ordered vector space over the ordered field $\mathbb {R}$
 is a Hahn space over $\mathbb {R}$
is a Hahn space over $\mathbb {R}$ .
.(4) The ordered $\mathbb {Q}$
 -vector space $\mathbb {Q}+\mathbb {Q}\sqrt 2 \subseteq \mathbb {R}$
-vector space $\mathbb {Q}+\mathbb {Q}\sqrt 2 \subseteq \mathbb {R}$ is not a Hahn space over $\mathbb {Q}$
is not a Hahn space over $\mathbb {Q}$ .
.
We say that an $H$![]() -couple $(\Gamma,\,\psi )$
-couple $(\Gamma,\,\psi )$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() is of Hahn type if for all $\alpha,\,\beta \in \Gamma ^{\ne }$
is of Hahn type if for all $\alpha,\,\beta \in \Gamma ^{\ne }$![]() with $\psi (\alpha )=\psi (\beta )$
with $\psi (\alpha )=\psi (\beta )$![]() there exists a scalar $c\in {\boldsymbol {k}}$
there exists a scalar $c\in {\boldsymbol {k}}$![]() such that $\psi (\alpha -c\beta )> \psi (\alpha )$
such that $\psi (\alpha -c\beta )> \psi (\alpha )$![]() ; equivalently, $\Gamma$
; equivalently, $\Gamma$![]() is a Hahn space over ${\boldsymbol {k}}$
is a Hahn space over ${\boldsymbol {k}}$![]() and for all $\alpha,\,\beta \in \Gamma ^{\ne }$
and for all $\alpha,\,\beta \in \Gamma ^{\ne }$![]() ,
,
Let $K$![]() be a Liouville closed $H$
be a Liouville closed $H$![]() -field. We made its $H$
-field. We made its $H$![]() -couple $(\Gamma,\, \psi )$
-couple $(\Gamma,\, \psi )$![]() into an $H$
into an $H$![]() -couple over its constant field $C$
-couple over its constant field $C$![]() , and as such $(\Gamma,\,\psi )$
, and as such $(\Gamma,\,\psi )$![]() is of Hahn type.
is of Hahn type.
Details on the example in the introduction
We consider the Liouville closed $H$![]() -field $\mathbb {T}$
-field $\mathbb {T}$![]() and its element $x$
and its element $x$![]() with $x'=1$
with $x'=1$![]() . For $z\in \mathbb {T}$
. For $z\in \mathbb {T}$![]() with $z'\notin \mathbb {R}$
with $z'\notin \mathbb {R}$![]() we have
we have

Considering also the case where $z'\in \mathbb {R}$![]() we conclude that
we conclude that
Next, let $y\in \mathbb {T}^\times$![]() and suppose $z:=y^{\dagger}$
and suppose $z:=y^{\dagger}$![]() satisfies $zz''=(z')^2$
satisfies $zz''=(z')^2$![]() . Then $y=r\operatorname {e}^{u}$
. Then $y=r\operatorname {e}^{u}$![]() for some $r\in \mathbb {R}$
for some $r\in \mathbb {R}$![]() and $u\in \mathbb {T}$
and $u\in \mathbb {T}$![]() with $u'=z$
with $u'=z$![]() . For $z=s\operatorname {e}^{tx}$
. For $z=s\operatorname {e}^{tx}$![]() with $s,\,t\in \mathbb {R}$
with $s,\,t\in \mathbb {R}$![]() and $u\in \mathbb {T}$
and $u\in \mathbb {T}$![]() , $u'=z$
, $u'=z$![]() we get $u\in \mathbb {R}\operatorname {e}^{tx}+\mathbb {R}$
we get $u\in \mathbb {R}\operatorname {e}^{tx}+\mathbb {R}$![]() if $t\ne 0$
if $t\ne 0$![]() , and $u\in \mathbb {R} x+\mathbb {R}$
, and $u\in \mathbb {R} x+\mathbb {R}$![]() if $t=0$
if $t=0$![]() . Hence $y=a\operatorname {e}^{b\operatorname {e}^{cx}}$
. Hence $y=a\operatorname {e}^{b\operatorname {e}^{cx}}$![]() or $y=a\operatorname {e}^{bx}$
or $y=a\operatorname {e}^{bx}$![]() for some $a,\,b,\,c\in \mathbb {R}$
for some $a,\,b,\,c\in \mathbb {R}$![]() . From $zz''=(z')^2$
. From $zz''=(z')^2$![]() we get
we get
In this way, we get for
that its set of zeros in $\mathbb {T}$![]() is
is
It is easy to see that for $0< c < d$![]() in $\mathbb {R}$
in $\mathbb {R}$![]() we have $[v(\operatorname {e}^{\operatorname {e}^{cx}})]_{\mathbb {R}} < [v(\operatorname {e}^{\operatorname {e}^{dx}})]_{\mathbb {R}}$
we have $[v(\operatorname {e}^{\operatorname {e}^{cx}})]_{\mathbb {R}} < [v(\operatorname {e}^{\operatorname {e}^{dx}})]_{\mathbb {R}}$![]() , so the set $\big \{vy:\, y\in \mathbb {T}^\times,\,\ G(y)=0\big \}$
, so the set $\big \{vy:\, y\in \mathbb {T}^\times,\,\ G(y)=0\big \}$![]() is not contained in a finite-dimensional $\mathbb {R}$
is not contained in a finite-dimensional $\mathbb {R}$![]() -linear subspace of $\Gamma _{\mathbb {T}}$
-linear subspace of $\Gamma _{\mathbb {T}}$![]() .
.
2. Extensions of $H$ -couples
-couples
In this section, $(\Gamma,\,\psi )$![]() and $(\Gamma _1,\, \psi _1)$
and $(\Gamma _1,\, \psi _1)$![]() are $H$
are $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() . An embedding
. An embedding
is an embedding $h \colon \Gamma \to \Gamma _1$![]() of ordered vector spaces over ${\boldsymbol {k}}$
of ordered vector spaces over ${\boldsymbol {k}}$![]() such that
such that
If $\Gamma \subseteq \Gamma _1$![]() and the inclusion $\Gamma \hookrightarrow \Gamma _1$
and the inclusion $\Gamma \hookrightarrow \Gamma _1$![]() is an embedding $(\Gamma,\,\psi ) \to (\Gamma _1,\,\psi _1)$
is an embedding $(\Gamma,\,\psi ) \to (\Gamma _1,\,\psi _1)$![]() , then we call $(\Gamma _1,\,\psi _1)$
, then we call $(\Gamma _1,\,\psi _1)$![]() an extension of $(\Gamma,\,\psi )$
an extension of $(\Gamma,\,\psi )$![]() . If $(\Gamma _1,\, \psi _1)$
. If $(\Gamma _1,\, \psi _1)$![]() is of Hahn type and extends $(\Gamma,\, \psi )$
is of Hahn type and extends $(\Gamma,\, \psi )$![]() , then $(\Gamma,\, \psi )$
, then $(\Gamma,\, \psi )$![]() is of Hahn type.
is of Hahn type.
Embedding lemmas
The lemmas in this subsection are the analogues for $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() of similar lemmas for $H$
of similar lemmas for $H$![]() -couples in [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.8]. The proofs are essentially the same, so we omit them.
-couples in [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.8]. The proofs are essentially the same, so we omit them.
Lemma 2.1 Let $\beta$![]() be a gap in $(\Gamma,\, \psi )$
be a gap in $(\Gamma,\, \psi )$![]() . Then there is an $H$
. Then there is an $H$![]() -couple ${(\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha })}$
-couple ${(\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha })}$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() that extends $(\Gamma,\,\psi )$
that extends $(\Gamma,\,\psi )$![]() such that:
such that:
(i) $\alpha >0$
 and $\alpha '=\beta ;$
and $\alpha '=\beta ;$
(ii) if $i\colon (\Gamma,\,\psi )\to (\Gamma _1,\,\psi _1)$
 is an embedding and $\alpha _1\in \Gamma _1,$
is an embedding and $\alpha _1\in \Gamma _1,$ $\alpha _1>0,$
$\alpha _1>0,$ $\alpha _1'=i(\beta ),$
$\alpha _1'=i(\beta ),$ then $i$
then $i$ extends uniquely to an embedding $j\colon \bigl (\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha }\bigr )\to (\Gamma _1,\,\psi _1)$
extends uniquely to an embedding $j\colon \bigl (\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha }\bigr )\to (\Gamma _1,\,\psi _1)$ with $j(\alpha )=\alpha _1$
with $j(\alpha )=\alpha _1$ .
.
The universal property (ii) determines $(\Gamma +{\boldsymbol {k}}\alpha,\, \psi ^{\alpha })$![]() up to isomorphism over $(\Gamma,\, \psi )$
up to isomorphism over $(\Gamma,\, \psi )$![]() , and $0< c\alpha < \Gamma ^{>}$
, and $0< c\alpha < \Gamma ^{>}$![]() for all $c\in {\boldsymbol {k}}^{>}$
for all $c\in {\boldsymbol {k}}^{>}$![]() ; moreover, for all $\gamma \in \Gamma$
; moreover, for all $\gamma \in \Gamma$![]() and $c\in {\boldsymbol {k}}$
and $c\in {\boldsymbol {k}}$![]() with $\gamma +c\alpha \ne 0$
with $\gamma +c\alpha \ne 0$![]() ,
,

Note also that $[\Gamma + {\boldsymbol {k}}\alpha ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\alpha ]_{{\boldsymbol {k}}}\big \}$![]() , so for $\Psi ^{\alpha }:=\psi ^{\alpha }((\Gamma +{\boldsymbol {k}}\alpha )^{\ne })$
, so for $\Psi ^{\alpha }:=\psi ^{\alpha }((\Gamma +{\boldsymbol {k}}\alpha )^{\ne })$![]() we have:
we have:
Lemma 2.1 goes through with $\alpha < 0$![]() and $\alpha _1 <0$
and $\alpha _1 <0$![]() in place of $\alpha >0$
in place of $\alpha >0$![]() and $\alpha _1 > 0$
and $\alpha _1 > 0$![]() , respectively. In the setting of this modified lemma, we have $\Gamma ^{<} < c\alpha < 0$
, respectively. In the setting of this modified lemma, we have $\Gamma ^{<} < c\alpha < 0$![]() for all $c\in {\boldsymbol {k}}^{>}$
for all $c\in {\boldsymbol {k}}^{>}$![]() , (1) goes through for $\gamma \in \Gamma$
, (1) goes through for $\gamma \in \Gamma$![]() and $c\in {\boldsymbol {k}}$
and $c\in {\boldsymbol {k}}$![]() with $\gamma + c\alpha \ne 0$
with $\gamma + c\alpha \ne 0$![]() , (2) goes through. So we have two ways to remove a gap. Removal of a gap as above leads by (2) to a grounded $H$
, (2) goes through. So we have two ways to remove a gap. Removal of a gap as above leads by (2) to a grounded $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() , and this is the situation we consider next.
, and this is the situation we consider next.
Lemma 2.2 Assume that $\Psi$![]() has a largest element $\beta$
has a largest element $\beta$![]() . Then there exists an $H$
. Then there exists an $H$![]() -couple ${(\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha })}$
-couple ${(\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha })}$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() that extends $(\Gamma,\,\psi )$
that extends $(\Gamma,\,\psi )$![]() with $\alpha \ne 0,$
with $\alpha \ne 0,$![]() $\alpha '=\beta,$
$\alpha '=\beta,$![]() such that for any embedding $i\colon (\Gamma,\,\psi )\to (\Gamma _1,\,\psi _1)$
such that for any embedding $i\colon (\Gamma,\,\psi )\to (\Gamma _1,\,\psi _1)$![]() and any $\alpha _1\in \Gamma _1^{\ne }$
and any $\alpha _1\in \Gamma _1^{\ne }$![]() with $\alpha _1'=i(\beta )$
with $\alpha _1'=i(\beta )$![]() there is a unique extension of $i$
there is a unique extension of $i$![]() to an embedding $j\colon (\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha })\to (\Gamma _1,\,\psi _1)$
to an embedding $j\colon (\Gamma +{\boldsymbol {k}} \alpha,\, \psi ^{\alpha })\to (\Gamma _1,\,\psi _1)$![]() with $j(\alpha )=\alpha _1$
with $j(\alpha )=\alpha _1$![]() .
.
Let $(\Gamma +{\boldsymbol {k}}\alpha,\, \psi ^{\alpha })$![]() be as in Lemma 2.2. Then $\Gamma ^{<} < c\alpha < 0$
be as in Lemma 2.2. Then $\Gamma ^{<} < c\alpha < 0$![]() for all $c\in {\boldsymbol {k}}^{>}$
for all $c\in {\boldsymbol {k}}^{>}$![]() , $[\Gamma +{\boldsymbol {k}}\alpha ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\alpha ]_{{\boldsymbol {k}}}\big \}$
, $[\Gamma +{\boldsymbol {k}}\alpha ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\alpha ]_{{\boldsymbol {k}}}\big \}$![]() , so (2) holds for $\Psi ^{\alpha }:=\psi ^{\alpha }((\Gamma +{\boldsymbol {k}}\alpha )^{\ne })$
, so (2) holds for $\Psi ^{\alpha }:=\psi ^{\alpha }((\Gamma +{\boldsymbol {k}}\alpha )^{\ne })$![]() . Thus, our new $\Psi$
. Thus, our new $\Psi$![]() -set $\Psi ^{\alpha }$
-set $\Psi ^{\alpha }$![]() still has a maximum, but this maximum is larger than the maximum $\beta$
still has a maximum, but this maximum is larger than the maximum $\beta$![]() of the original $\Psi$
of the original $\Psi$![]() -set $\Psi$
-set $\Psi$![]() . By iterating this construction indefinitely and taking a union, we obtain an $H$
. By iterating this construction indefinitely and taking a union, we obtain an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() with asymptotic integration.
with asymptotic integration.
Once we have an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() with asymptotic integration, we can create an extension with a gap as follows:
with asymptotic integration, we can create an extension with a gap as follows:
Lemma 2.3 Suppose that $(\Gamma,\, \psi )$![]() has asymptotic integration. Then there is an $H$
has asymptotic integration. Then there is an $H$![]() -couple $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$
-couple $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() extending $(\Gamma,\, \psi )$
extending $(\Gamma,\, \psi )$![]() such that:
such that:
(i) $\Psi < \beta < (\Gamma ^{>})';$

(ii) for any $(\Gamma _1,\, \psi _1)$
 extending $(\Gamma,\, \psi )$
extending $(\Gamma,\, \psi )$ and $\beta _1\in \Gamma _1$
and $\beta _1\in \Gamma _1$ with $\Psi < \beta _1 < (\Gamma ^{>})'$
with $\Psi < \beta _1 < (\Gamma ^{>})'$ there is a unique embedding $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })\to (\Gamma _1,\, \psi _1)$
there is a unique embedding $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })\to (\Gamma _1,\, \psi _1)$ of $H$
of $H$ -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$ that is the identity on $\Gamma$
that is the identity on $\Gamma$ and sends $\beta$
and sends $\beta$ to $\beta _1$
to $\beta _1$ .
.
Let $(\Gamma,\, \psi )$![]() and $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$
and $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$![]() be as in Lemma 2.3. If $(\Gamma + {\boldsymbol {k}}\alpha,\, \psi _{\alpha })$
be as in Lemma 2.3. If $(\Gamma + {\boldsymbol {k}}\alpha,\, \psi _{\alpha })$![]() is also an $H$
is also an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() extending $(\Gamma,\, \psi )$
extending $(\Gamma,\, \psi )$![]() with $\Psi < \alpha < (\Gamma ^{>})'$
with $\Psi < \alpha < (\Gamma ^{>})'$![]() , then by (ii) we have an isomorphism $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })\to (\Gamma + {\boldsymbol {k}}\alpha,\, \psi _{\alpha })$
, then by (ii) we have an isomorphism $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })\to (\Gamma + {\boldsymbol {k}}\alpha,\, \psi _{\alpha })$![]() of $H$
of $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() and sends $\beta$
and sends $\beta$![]() to $\alpha$
to $\alpha$![]() . In this sense, $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$
. In this sense, $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$![]() is unique up to isomorphism over $(\Gamma,\, \psi )$
is unique up to isomorphism over $(\Gamma,\, \psi )$![]() . The construction of $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$
. The construction of $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$![]() gives the following extra information, with $\Psi _{\beta }$
gives the following extra information, with $\Psi _{\beta }$![]() the set of values of $\psi _{\beta }$
the set of values of $\psi _{\beta }$![]() on $(\Gamma + {\boldsymbol {k}}\beta )^{\ne }$
on $(\Gamma + {\boldsymbol {k}}\beta )^{\ne }$![]() :
:
Corollary 2.4 The set $\Gamma$![]() is dense in the ordered abelian group $\Gamma + {\boldsymbol {k}}\beta$
is dense in the ordered abelian group $\Gamma + {\boldsymbol {k}}\beta$![]() , so $[\Gamma ]_{{\boldsymbol {k}}} = [\Gamma + {\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}},$
, so $[\Gamma ]_{{\boldsymbol {k}}} = [\Gamma + {\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}},$![]() $\Psi _{\beta }=\Psi$
$\Psi _{\beta }=\Psi$![]() and $\beta$
and $\beta$![]() is a gap in $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$
is a gap in $(\Gamma + {\boldsymbol {k}}\beta,\, \psi _{\beta })$![]() .
.
Recall that a cut in an ordered set $S$![]() is just a downward closed subset of $S$
is just a downward closed subset of $S$![]() , and that an element $a$
, and that an element $a$![]() of an ordered set extending $S$
of an ordered set extending $S$![]() is said to realize a cut $D$
is said to realize a cut $D$![]() in $S$
in $S$![]() if $D< a< S\setminus D$
if $D< a< S\setminus D$![]() (so $a\notin S$
(so $a\notin S$![]() ).
).
Lemma 2.5 Let $D$![]() be a cut in $[\Gamma ^{\ne }]_{{\boldsymbol {k}}}$
be a cut in $[\Gamma ^{\ne }]_{{\boldsymbol {k}}}$![]() and let $\beta \in \Gamma$
and let $\beta \in \Gamma$![]() be such that $\beta <(\Gamma ^{>})'$
be such that $\beta <(\Gamma ^{>})'$![]() , $\gamma ^{\dagger} \leqslant \beta$
, $\gamma ^{\dagger} \leqslant \beta$![]() for all $\gamma \in \Gamma ^{\ne }$
for all $\gamma \in \Gamma ^{\ne }$![]() with $[\gamma ]_{{\boldsymbol {k}}}> D$
with $[\gamma ]_{{\boldsymbol {k}}}> D$![]() , and $\beta \leqslant \delta ^{\dagger}$
, and $\beta \leqslant \delta ^{\dagger}$![]() for all $\delta \in \Gamma ^{\ne }$
for all $\delta \in \Gamma ^{\ne }$![]() with $[\delta ]_{{\boldsymbol {k}}}\in D$
with $[\delta ]_{{\boldsymbol {k}}}\in D$![]() . Then there exists an $H$
. Then there exists an $H$![]() -couple $(\Gamma \oplus {\boldsymbol {k}}\alpha,\,\psi ^\alpha )$
-couple $(\Gamma \oplus {\boldsymbol {k}}\alpha,\,\psi ^\alpha )$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() that extends $(\Gamma,\,\psi ),$
that extends $(\Gamma,\,\psi ),$![]() with $\alpha >0,$
with $\alpha >0,$![]() such that:
such that:
(i) $[\alpha ]_{\boldsymbol {k}}$
 realizes the cut $D$
realizes the cut $D$ in $[\Gamma ^{\ne }]_{\boldsymbol {k}},$
in $[\Gamma ^{\ne }]_{\boldsymbol {k}},$ and $\psi ^\alpha (\alpha )=\beta ;$
and $\psi ^\alpha (\alpha )=\beta ;$
(ii) for any embedding $i\colon (\Gamma,\,\psi )\to (\Gamma _1,\,\psi _1)$
 and $\alpha _1\in \Gamma _1^{>}$
and $\alpha _1\in \Gamma _1^{>}$ such that $[\alpha _1]_{\boldsymbol {k}}$
such that $[\alpha _1]_{\boldsymbol {k}}$ realizes the cut $\bigl \{\bigl [i(\delta )\bigr ]_{\boldsymbol {k}}: [\delta ]_{\boldsymbol {k}}\in D\bigr \}$
realizes the cut $\bigl \{\bigl [i(\delta )\bigr ]_{\boldsymbol {k}}: [\delta ]_{\boldsymbol {k}}\in D\bigr \}$ in $\bigl [i(\Gamma ^{\ne })\bigr ]_{\boldsymbol {k}}$
in $\bigl [i(\Gamma ^{\ne })\bigr ]_{\boldsymbol {k}}$ and $\psi _1(\alpha _1)=i(\beta ),$
and $\psi _1(\alpha _1)=i(\beta ),$ $i$
$i$ extends uniquely to an embedding $j\colon {(\Gamma \oplus {\boldsymbol {k}}\alpha,\,\psi ^\alpha )}\to (\Gamma _1,\,\psi _1)$
extends uniquely to an embedding $j\colon {(\Gamma \oplus {\boldsymbol {k}}\alpha,\,\psi ^\alpha )}\to (\Gamma _1,\,\psi _1)$ with $j(\alpha )= \alpha _1$
with $j(\alpha )= \alpha _1$ .
.
Moreover, $[\Gamma \oplus {\boldsymbol {k}}\alpha ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\alpha ]_{{\boldsymbol {k}}}\big \}$![]() and $\Psi ^{\alpha }:=\psi ^{\alpha }((\Gamma \oplus {\boldsymbol {k}}\alpha )^{\ne })=\Psi \cup \{\beta \}$
and $\Psi ^{\alpha }:=\psi ^{\alpha }((\Gamma \oplus {\boldsymbol {k}}\alpha )^{\ne })=\Psi \cup \{\beta \}$![]() . If $(\Gamma,\, \psi )$
. If $(\Gamma,\, \psi )$![]() is grounded, then so is $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^\alpha )$
is grounded, then so is $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^\alpha )$![]() . If $(\Gamma,\,\psi )$
. If $(\Gamma,\,\psi )$![]() has asymptotic integration, then so does $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^\alpha )$
has asymptotic integration, then so does $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^\alpha )$![]() . If $\beta \in \Psi ^{\downarrow }$
. If $\beta \in \Psi ^{\downarrow }$![]() , then a gap in $(\Gamma,\,\psi )$
, then a gap in $(\Gamma,\,\psi )$![]() remains a gap in $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha })$
remains a gap in $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha })$![]() .
.
Proof. By a straightforward analogue of [Reference Aschenbrenner, van den Dries and van der Hoeven2, Lemma 2.4.5] we extend $\Gamma$![]() to an ordered vector space $\Gamma ^{\alpha }=\Gamma \oplus {\boldsymbol {k}}\alpha$
to an ordered vector space $\Gamma ^{\alpha }=\Gamma \oplus {\boldsymbol {k}}\alpha$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() with $\alpha >0$
with $\alpha >0$![]() such that $[\alpha ]_{{\boldsymbol {k}}}$
such that $[\alpha ]_{{\boldsymbol {k}}}$![]() realizes the cut $D$
realizes the cut $D$![]() in $[\Gamma ^{\ne }]_{{\boldsymbol {k}}}$
in $[\Gamma ^{\ne }]_{{\boldsymbol {k}}}$![]() . Then $[\Gamma \oplus {\boldsymbol {k}}\alpha ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\alpha ]_{{\boldsymbol {k}}}\big \}$
. Then $[\Gamma \oplus {\boldsymbol {k}}\alpha ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\alpha ]_{{\boldsymbol {k}}}\big \}$![]() . We extend $\psi$
. We extend $\psi$![]() to $\psi ^{\alpha }\colon (\Gamma ^{\alpha })^{\ne } \to \Gamma$
to $\psi ^{\alpha }\colon (\Gamma ^{\alpha })^{\ne } \to \Gamma$![]() by
by
Apart from some obvious changes, we now follow the proof of [Reference Aschenbrenner, van den Dries and van der Hoeven2, Lemma 9.8.7]. This gives the desired results, except for the last Claim of the lemma. To prove that claim, let $\beta \in \Psi ^{\downarrow }$![]() , let $\gamma \in \Gamma$
, let $\gamma \in \Gamma$![]() be a gap in $(\Gamma,\,\psi )$
be a gap in $(\Gamma,\,\psi )$![]() , and assume towards a contradiction that $\gamma$
, and assume towards a contradiction that $\gamma$![]() is not a gap in $(\Gamma ^{\alpha },\,\psi ^{\alpha })$
is not a gap in $(\Gamma ^{\alpha },\,\psi ^{\alpha })$![]() . Then $\gamma > \Psi ^\alpha$
. Then $\gamma > \Psi ^\alpha$![]() , so $\gamma =(\delta +c\alpha )'$
, so $\gamma =(\delta +c\alpha )'$![]() with $\delta \in \Gamma$
with $\delta \in \Gamma$![]() , $c\in {\boldsymbol {k}}^\times$
, $c\in {\boldsymbol {k}}^\times$![]() and $0 <\delta +c\alpha < \Gamma ^{>}$
and $0 <\delta +c\alpha < \Gamma ^{>}$![]() . Then $[\delta +c\alpha ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
. Then $[\delta +c\alpha ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() , so $[\delta +c\alpha ]_{{\boldsymbol {k}}}=[\alpha ]_{{\boldsymbol {k}}}$
, so $[\delta +c\alpha ]_{{\boldsymbol {k}}}=[\alpha ]_{{\boldsymbol {k}}}$![]() . As $\Psi$
. As $\Psi$![]() has no largest element, we get $\Psi < (\delta +c\alpha )^{\dagger} =\alpha ^{\dagger} =\beta$
has no largest element, we get $\Psi < (\delta +c\alpha )^{\dagger} =\alpha ^{\dagger} =\beta$![]() , a contradiction.
, a contradiction.
The case of Hahn type
In Lemma 2.1 (and in its variant with $\alpha <0$![]() ), in Lemma 2.2, and in Lemma 2.5 for $\beta \notin \Psi$
), in Lemma 2.2, and in Lemma 2.5 for $\beta \notin \Psi$![]() , we have:
, we have:
Suppose $(\Gamma,\, \psi )$![]() and $(\Gamma +{\boldsymbol {k}}\beta,\, \psi _{\beta })$
and $(\Gamma +{\boldsymbol {k}}\beta,\, \psi _{\beta })$![]() are as in Lemma 2.3, and $(\Gamma,\,\psi )$
are as in Lemma 2.3, and $(\Gamma,\,\psi )$![]() is of Hahn type. We claim that then $(\Gamma +{\boldsymbol {k}}\beta,\, \psi _{\beta })$
is of Hahn type. We claim that then $(\Gamma +{\boldsymbol {k}}\beta,\, \psi _{\beta })$![]() is also of Hahn type. To prove this claim, recall from Corollary 2.4 that $\Gamma$
is also of Hahn type. To prove this claim, recall from Corollary 2.4 that $\Gamma$![]() is dense in $\Gamma +{\boldsymbol {k}}\beta$
is dense in $\Gamma +{\boldsymbol {k}}\beta$![]() . It follows easily that for non-zero $\alpha _1,\, \alpha _2\in \Gamma +{\boldsymbol {k}}\beta$
. It follows easily that for non-zero $\alpha _1,\, \alpha _2\in \Gamma +{\boldsymbol {k}}\beta$![]() with $\psi _{\beta }(\alpha _1)=\psi _{\beta }(\alpha _2)$
with $\psi _{\beta }(\alpha _1)=\psi _{\beta }(\alpha _2)$![]() we have $[\alpha _1]_{{\boldsymbol {k}}}=[\alpha _2]_{{\boldsymbol {k}}}$
we have $[\alpha _1]_{{\boldsymbol {k}}}=[\alpha _2]_{{\boldsymbol {k}}}$![]() . It remains to show that $\Gamma +{\boldsymbol {k}}\beta$
. It remains to show that $\Gamma +{\boldsymbol {k}}\beta$![]() is a Hahn space over ${\boldsymbol {k}}$
is a Hahn space over ${\boldsymbol {k}}$![]() . So let $\alpha _1,\, \alpha _2\in \Gamma +{\boldsymbol {k}}\beta$
. So let $\alpha _1,\, \alpha _2\in \Gamma +{\boldsymbol {k}}\beta$![]() be non-zero with $[\alpha _1]_{{\boldsymbol {k}}}=[\alpha _2]_{{\boldsymbol {k}}}$
be non-zero with $[\alpha _1]_{{\boldsymbol {k}}}=[\alpha _2]_{{\boldsymbol {k}}}$![]() . By density again, and the fact that $[\Gamma ]_{{\boldsymbol {k}}}=[\Gamma +{\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}$
. By density again, and the fact that $[\Gamma ]_{{\boldsymbol {k}}}=[\Gamma +{\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}$![]() has no least element $> [0]_{{\boldsymbol {k}}}$
has no least element $> [0]_{{\boldsymbol {k}}}$![]() , we have $\gamma _1,\, \gamma _2\in \Gamma$
, we have $\gamma _1,\, \gamma _2\in \Gamma$![]() such that $[\alpha _1-\gamma _1]_{{\boldsymbol {k}}}< [\alpha _1]_{{\boldsymbol {k}}}$
such that $[\alpha _1-\gamma _1]_{{\boldsymbol {k}}}< [\alpha _1]_{{\boldsymbol {k}}}$![]() and $[\alpha _2-\gamma _2]_{{\boldsymbol {k}}}< [\alpha _2]_{{\boldsymbol {k}}}$
and $[\alpha _2-\gamma _2]_{{\boldsymbol {k}}}< [\alpha _2]_{{\boldsymbol {k}}}$![]() . Take $c\in {\boldsymbol {k}}^\times$
. Take $c\in {\boldsymbol {k}}^\times$![]() such that $[\gamma _1-c\gamma _2]_{{\boldsymbol {k}}}< [\gamma _1]_{{\boldsymbol {k}}}$
such that $[\gamma _1-c\gamma _2]_{{\boldsymbol {k}}}< [\gamma _1]_{{\boldsymbol {k}}}$![]() . It follows easily that then $[\alpha _1-c\alpha _2]_{{\boldsymbol {k}}}< [\alpha _1]_{{\boldsymbol {k}}}$
. It follows easily that then $[\alpha _1-c\alpha _2]_{{\boldsymbol {k}}}< [\alpha _1]_{{\boldsymbol {k}}}$![]() .
.
New extension lemmas
The three next lemmas will enable in the next section a simpler proof of QE for closed $H$![]() -couples than in [Reference Aschenbrenner and van den Dries1]: in that paper, we needed “properties (A) and (B)” with long and tedious proofs, and here we avoid this.
-couples than in [Reference Aschenbrenner and van den Dries1]: in that paper, we needed “properties (A) and (B)” with long and tedious proofs, and here we avoid this.
Lemma 2.6 Suppose $(\Gamma _1,\,\psi _1)$![]() extends $(\Gamma,\,\psi )$
extends $(\Gamma,\,\psi )$![]() . Let $\beta \in \Gamma _1\setminus \Gamma$
. Let $\beta \in \Gamma _1\setminus \Gamma$![]() and $\alpha _0\in \Gamma$
and $\alpha _0\in \Gamma$![]() be such that $(\beta -\alpha _0)^{\dagger} \notin \Gamma$
be such that $(\beta -\alpha _0)^{\dagger} \notin \Gamma$![]() . Then $(\beta -\alpha _0)^{\dagger} = \max \big \{(\beta -\alpha )^{\dagger} :\,\alpha \in \Gamma \big \}$
. Then $(\beta -\alpha _0)^{\dagger} = \max \big \{(\beta -\alpha )^{\dagger} :\,\alpha \in \Gamma \big \}$![]() . If in addition $\Gamma ^{<}$
. If in addition $\Gamma ^{<}$![]() is cofinal in $\Gamma _1^{<},$
is cofinal in $\Gamma _1^{<},$![]() then $(\beta -\alpha _0)^{\dagger} \leqslant \text { some element of }\Psi$
then $(\beta -\alpha _0)^{\dagger} \leqslant \text { some element of }\Psi$![]() .
.
Proof. Suppose $\alpha \in \Gamma$![]() and $(\beta -\alpha )^{\dagger} > (\beta -\alpha _0)^{\dagger}$
and $(\beta -\alpha )^{\dagger} > (\beta -\alpha _0)^{\dagger}$![]() . Then $\alpha -\alpha _0=(\beta -\alpha _0)-(\beta -\alpha )$
. Then $\alpha -\alpha _0=(\beta -\alpha _0)-(\beta -\alpha )$![]() gives $(\beta -\alpha _0)^{\dagger} =(\alpha -\alpha _0)^{\dagger} \in \Gamma$
gives $(\beta -\alpha _0)^{\dagger} =(\alpha -\alpha _0)^{\dagger} \in \Gamma$![]() , a contradiction. Assume $|\beta -\alpha _0|\geqslant |\gamma |$
, a contradiction. Assume $|\beta -\alpha _0|\geqslant |\gamma |$![]() , $\gamma \in \Gamma ^{\ne }$
, $\gamma \in \Gamma ^{\ne }$![]() . Then $(\beta -\alpha _0)^{\dagger} \leqslant \gamma ^{\dagger} \in \Psi$
. Then $(\beta -\alpha _0)^{\dagger} \leqslant \gamma ^{\dagger} \in \Psi$![]() .
.
Lemma 2.7 Suppose $(\Gamma,\,\psi )$![]() is closed and $(\Gamma _1,\, \psi _1)$
is closed and $(\Gamma _1,\, \psi _1)$![]() and $(\Gamma _*,\,\psi _*)$
and $(\Gamma _*,\,\psi _*)$![]() are $H$
are $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() extending $(\Gamma,\,\psi )$
extending $(\Gamma,\,\psi )$![]() . Let $\beta \in \Gamma _1\setminus \Gamma$
. Let $\beta \in \Gamma _1\setminus \Gamma$![]() and $\beta _*\in \Gamma _*\setminus \Gamma$
and $\beta _*\in \Gamma _*\setminus \Gamma$![]() realize the same cut in $\Gamma$
realize the same cut in $\Gamma$![]() , and suppose that $\beta ^{\dagger} \notin \Gamma$
, and suppose that $\beta ^{\dagger} \notin \Gamma$![]() and $\Gamma ^{<}$
and $\Gamma ^{<}$![]() are cofinal in $(\Gamma +{\boldsymbol {k}}\beta ^{\dagger} )^{<}$
are cofinal in $(\Gamma +{\boldsymbol {k}}\beta ^{\dagger} )^{<}$![]() . Then $\beta _*^{\dagger} \notin \Gamma,$
. Then $\beta _*^{\dagger} \notin \Gamma,$![]() and $\beta ^{\dagger}$
and $\beta ^{\dagger}$![]() and $\beta _*^{\dagger}$
and $\beta _*^{\dagger}$![]() realize the same cut in $\Gamma$
realize the same cut in $\Gamma$![]() .
.
Proof. Let $\alpha \in \Gamma ^{\ne }$![]() . We claim:
. We claim:
To prove the first implication, assume $\beta ^{\dagger} <\alpha ^{\dagger}$![]() . Then $|\beta |>|\alpha |$
. Then $|\beta |>|\alpha |$![]() , so $|\beta _*|>|\alpha |$
, so $|\beta _*|>|\alpha |$![]() , and thus $\beta _*^{\dagger} \leqslant \alpha ^{\dagger}$
, and thus $\beta _*^{\dagger} \leqslant \alpha ^{\dagger}$![]() . Since $(\Gamma,\,\psi )$
. Since $(\Gamma,\,\psi )$![]() is closed and $\Gamma ^{<}$
is closed and $\Gamma ^{<}$![]() is cofinal in $(\Gamma +{\boldsymbol {k}}\beta ^{\dagger} )^{<}$
is cofinal in $(\Gamma +{\boldsymbol {k}}\beta ^{\dagger} )^{<}$![]() , we can replace in this argument $\alpha$
, we can replace in this argument $\alpha$![]() by some $\gamma \in \Gamma ^{\ne }$
by some $\gamma \in \Gamma ^{\ne }$![]() with $\beta ^{\dagger} <\gamma ^{\dagger} <\alpha ^{\dagger}$
with $\beta ^{\dagger} <\gamma ^{\dagger} <\alpha ^{\dagger}$![]() , to get $\beta _*^{\dagger} \leqslant \gamma ^{\dagger} <\alpha ^{\dagger}$
, to get $\beta _*^{\dagger} \leqslant \gamma ^{\dagger} <\alpha ^{\dagger}$![]() , and thus $\beta _*^{\dagger} <\alpha ^{\dagger}$
, and thus $\beta _*^{\dagger} <\alpha ^{\dagger}$![]() as claimed. The second implication follows in the same way.
as claimed. The second implication follows in the same way.
If $\beta ^{\dagger} < \gamma ^{\dagger}$![]() for some $\gamma \in \Gamma ^{\ne }$
for some $\gamma \in \Gamma ^{\ne }$![]() , then $(\Gamma,\,\psi )$
, then $(\Gamma,\,\psi )$![]() being closed gives the desired conclusion. If $\beta ^{\dagger} >\Psi$
being closed gives the desired conclusion. If $\beta ^{\dagger} >\Psi$![]() , then we use instead $\Psi < \beta ^{\dagger} < (\Gamma ^{>})'$
, then we use instead $\Psi < \beta ^{\dagger} < (\Gamma ^{>})'$![]() and $\Psi < \beta _*^{\dagger} < (\Gamma ^{>})'$
and $\Psi < \beta _*^{\dagger} < (\Gamma ^{>})'$![]() .
.
Lemma 2.8 Suppose $(\Gamma _1,\,\psi _1)$![]() extends $(\Gamma,\,\psi )$
extends $(\Gamma,\,\psi )$![]() . Let $\beta \in \Gamma _1\setminus \Gamma$
. Let $\beta \in \Gamma _1\setminus \Gamma$![]() and $\alpha _0,\, \alpha _1\in \Gamma$
and $\alpha _0,\, \alpha _1\in \Gamma$![]() be such that $\beta _0^{\dagger} \notin \Gamma$
be such that $\beta _0^{\dagger} \notin \Gamma$![]() for $\beta _0:= \beta -\alpha _0$
for $\beta _0:= \beta -\alpha _0$![]() and $\beta _1^{\dagger} \notin \Psi$
and $\beta _1^{\dagger} \notin \Psi$![]() for $\beta _1:=\beta _0^{\dagger} -\alpha _1$
for $\beta _1:=\beta _0^{\dagger} -\alpha _1$![]() . Assume also that $|\beta _0|\geqslant |\alpha |$
. Assume also that $|\beta _0|\geqslant |\alpha |$![]() for some $\alpha \in \Gamma ^{\ne }$
for some $\alpha \in \Gamma ^{\ne }$![]() . Then $\beta _0^{\dagger} < \beta _1^{\dagger}$
. Then $\beta _0^{\dagger} < \beta _1^{\dagger}$![]() .
.
Proof. From $|\beta _0|\geqslant |\alpha |$![]() with $\alpha \in \Gamma ^{\ne }$
with $\alpha \in \Gamma ^{\ne }$![]() we get $\beta _0^{\dagger} \leqslant \alpha ^{\dagger}$
we get $\beta _0^{\dagger} \leqslant \alpha ^{\dagger}$![]() . Also, $\beta _0^{\dagger} -\alpha ^{\dagger} \notin \Gamma$
. Also, $\beta _0^{\dagger} -\alpha ^{\dagger} \notin \Gamma$![]() and ${[\beta _0^{\dagger} -\alpha _1]_{{\boldsymbol {k}}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
and ${[\beta _0^{\dagger} -\alpha _1]_{{\boldsymbol {k}}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() , hence $[\beta _0^{\dagger} -\alpha ^{\dagger} ]_{{\boldsymbol {k}}}\geqslant [\beta _0^{\dagger} -\alpha _1]_{{\boldsymbol {k}}}$
, hence $[\beta _0^{\dagger} -\alpha ^{\dagger} ]_{{\boldsymbol {k}}}\geqslant [\beta _0^{\dagger} -\alpha _1]_{{\boldsymbol {k}}}$![]() . In view of [Reference Aschenbrenner, van den Dries and van der Hoeven2, 6.5.4(i)], this gives
. In view of [Reference Aschenbrenner, van den Dries and van der Hoeven2, 6.5.4(i)], this gives
3. Eliminating quantifiers for closed $H$ -couples
-couples
Eliminating quantifiers for closed $H$![]() -couples requires a predicate for their $\Psi$
-couples requires a predicate for their $\Psi$![]() -set, and in this connection, we need to study the substructures of the thus expanded $H$
-set, and in this connection, we need to study the substructures of the thus expanded $H$![]() -couples. Accordingly, we define an $H$
-couples. Accordingly, we define an $H$![]() -triple over ${\boldsymbol {k}}$
-triple over ${\boldsymbol {k}}$![]() to be a triple $(\Gamma,\, \psi,\, P)$
to be a triple $(\Gamma,\, \psi,\, P)$![]() where $(\Gamma,\,\psi )$
where $(\Gamma,\,\psi )$![]() is an $H$
is an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() and $P\subseteq \Gamma$
and $P\subseteq \Gamma$![]() is an $H$
is an $H$![]() -cut in $(\Gamma,\,\psi )$
-cut in $(\Gamma,\,\psi )$![]() .
.
Lemma 3.1 Let $(\Gamma,\,\psi,\, P)$![]() be an $H$
be an $H$![]() -triple over ${\boldsymbol {k}},$
-triple over ${\boldsymbol {k}},$![]() and let $\beta \in P\setminus \Psi$
and let $\beta \in P\setminus \Psi$![]() . Then $(\Gamma,\,\psi,\, P)$
. Then $(\Gamma,\,\psi,\, P)$![]() can be extended to an $H$
can be extended to an $H$![]() -triple $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha },\, P^{\alpha })$
-triple $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha },\, P^{\alpha })$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() such that:
such that:
(i) $\alpha >0$
 and $\psi ^{\alpha }(\alpha )=\beta ;$
and $\psi ^{\alpha }(\alpha )=\beta ;$
(ii) given any embedding $i\colon (\Gamma,\, \psi,\, P)\to (\Gamma ^*,\, \psi ^*,\, P^*)$
 and any element $\alpha ^*>0$
and any element $\alpha ^*>0$ in $\Gamma ^*$
in $\Gamma ^*$ with $\psi ^*(\alpha ^*)=i(\beta )$
with $\psi ^*(\alpha ^*)=i(\beta )$ , there is a unique extension of $i$
, there is a unique extension of $i$ to an embedding $j\colon (\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha },\, P^{\alpha })\to (\Gamma ^*,\, \psi ^*,\, P^*)$
to an embedding $j\colon (\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha },\, P^{\alpha })\to (\Gamma ^*,\, \psi ^*,\, P^*)$ with $j(\alpha )=\alpha ^*$
with $j(\alpha )=\alpha ^*$ .
.
If $(\Gamma,\,\psi )$![]() is of Hahn type, then so is $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha })$
is of Hahn type, then so is $(\Gamma \oplus {\boldsymbol {k}}\alpha,\, \psi ^{\alpha })$![]() .
.
Proof. Distinguishing various cases this follows from Lemma 2.5, especially the claims beginning with “Moreover”. Use also “The case of Hahn type”.
An $H$![]() -closure of an $H$
-closure of an $H$![]() -triple $(\Gamma,\, \psi,\, P)$
-triple $(\Gamma,\, \psi,\, P)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() is defined to be a closed $H$
is defined to be a closed $H$![]() -triple $(\Gamma ^{\operatorname {c}},\, \psi ^{\operatorname {c}},\, P^{\operatorname {c}})$
-triple $(\Gamma ^{\operatorname {c}},\, \psi ^{\operatorname {c}},\, P^{\operatorname {c}})$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() that extends $(\Gamma,\,\psi,\,P)$
that extends $(\Gamma,\,\psi,\,P)$![]() such that any embedding
such that any embedding
into a closed $H$![]() -triple $(\Gamma ^*,\, \psi ^*,\, P^*)$
-triple $(\Gamma ^*,\, \psi ^*,\, P^*)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() extends to an embedding
extends to an embedding
Corollary 3.2 Every $H$![]() -triple over ${\boldsymbol {k}}$
-triple over ${\boldsymbol {k}}$![]() has an $H$
has an $H$![]() -closure. Every $H$
-closure. Every $H$![]() -triple over ${\boldsymbol {k}}$
-triple over ${\boldsymbol {k}}$![]() of Hahn type has an $H$
of Hahn type has an $H$![]() -closure that is of Hahn type.
-closure that is of Hahn type.
Proof. This is a straightforward consequence of Lemmas 2.1, 2.2, and 3.1, using for the second statement also the remarks in “The case of Hahn type”.
We consider $H$![]() -triples as $\mathcal {L}_{{\boldsymbol {k}}}$
-triples as $\mathcal {L}_{{\boldsymbol {k}}}$![]() -structures where $\mathcal {L}_{{\boldsymbol {k}}}$
-structures where $\mathcal {L}_{{\boldsymbol {k}}}$![]() is the natural language of ordered vector spaces over ${\boldsymbol {k}}$
is the natural language of ordered vector spaces over ${\boldsymbol {k}}$![]() , augmented by a constant symbol $\infty$
, augmented by a constant symbol $\infty$![]() , a unary function symbol $\psi$
, a unary function symbol $\psi$![]() , and a unary relation symbol $P$
, and a unary relation symbol $P$![]() . The underlying set of an $H$
. The underlying set of an $H$![]() -triple $(\Gamma,\, \psi,\, P)$
-triple $(\Gamma,\, \psi,\, P)$![]() , when construed as an $\mathcal {L}_{{\boldsymbol {k}}}$
, when construed as an $\mathcal {L}_{{\boldsymbol {k}}}$![]() -structure, is $\Gamma _{\infty }$
-structure, is $\Gamma _{\infty }$![]() rather than $\Gamma$
rather than $\Gamma$![]() , and the symbols of $\mathcal {L}_{{\boldsymbol {k}}}$
, and the symbols of $\mathcal {L}_{{\boldsymbol {k}}}$![]() are interpreted in $(\Gamma,\, \psi,\, P)$
are interpreted in $(\Gamma,\, \psi,\, P)$![]() as usual, with $\infty$
as usual, with $\infty$![]() serving as a default value:
serving as a default value:
for $\gamma \in \Gamma$![]() and $c\in {\boldsymbol {k}}$
and $c\in {\boldsymbol {k}}$![]() . Also $0^{\dagger} :=\infty$
. Also $0^{\dagger} :=\infty$![]() for the zero element $0\in \Gamma$
for the zero element $0\in \Gamma$![]() , so $\Gamma ^{\dagger} =\Psi \cup \{\infty \}$
, so $\Gamma ^{\dagger} =\Psi \cup \{\infty \}$![]() .
.
Theorem 3.3 The $\mathcal {L}_{{\boldsymbol {k}}}$![]() -theory of closed $H$
-theory of closed $H$![]() -triples over ${\boldsymbol {k}}$
-triples over ${\boldsymbol {k}}$![]() has $\operatorname {QE}$
has $\operatorname {QE}$![]() .
.
The proof of QE
Towards Theorem 3.3 we consider an $H$![]() -triple $(\Gamma,\, \psi,\, P)$
-triple $(\Gamma,\, \psi,\, P)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() and closed $H$
and closed $H$![]() -triples $(\Gamma _1,\, \psi _1,\, P_1)$
-triples $(\Gamma _1,\, \psi _1,\, P_1)$![]() and $(\Gamma _*,\, \psi _*,\, P_*)$
and $(\Gamma _*,\, \psi _*,\, P_*)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() that extend $(\Gamma,\, \psi,\, P)$
that extend $(\Gamma,\, \psi,\, P)$![]() , and such that $(\Gamma _*,\, \psi _*,\, P_*)$
, and such that $(\Gamma _*,\, \psi _*,\, P_*)$![]() is $|\Gamma |^+$
is $|\Gamma |^+$![]() -saturated. For $\gamma \in \Gamma _1$
-saturated. For $\gamma \in \Gamma _1$![]() we let $(\Gamma \langle \gamma \rangle,\, \psi _{\gamma })$
we let $(\Gamma \langle \gamma \rangle,\, \psi _{\gamma })$![]() be the $H$
be the $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() generated by $\Gamma \cup \{\gamma \}$
generated by $\Gamma \cup \{\gamma \}$![]() in $(\Gamma _1,\, \psi _1)$
in $(\Gamma _1,\, \psi _1)$![]() , and set $P_{\gamma }:= P_1\cap \Gamma \langle \gamma \rangle$
, and set $P_{\gamma }:= P_1\cap \Gamma \langle \gamma \rangle$![]() .
.
Let $\beta \in \Gamma _1\setminus \Gamma$![]() . Theorem 3.3 follows if we can show that under these assumptions $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$
. Theorem 3.3 follows if we can show that under these assumptions $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$![]() can be embedded over $\Gamma$
can be embedded over $\Gamma$![]() into $(\Gamma _*,\, \psi _*,\, P_*)$
into $(\Gamma _*,\, \psi _*,\, P_*)$![]() . We first do this in a situation that may seem rather special:
. We first do this in a situation that may seem rather special:
Lemma 3.4 Suppose $(\Gamma,\, \psi )$![]() has asymptotic integration and $(\Gamma + {\boldsymbol {k}}\beta )^{\dagger} =\Gamma ^{\dagger}$
has asymptotic integration and $(\Gamma + {\boldsymbol {k}}\beta )^{\dagger} =\Gamma ^{\dagger}$![]() . Then $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$
. Then $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$![]() can be embedded over $\Gamma$
can be embedded over $\Gamma$![]() into $(\Gamma _*,\, \psi _*,\, P_*)$
into $(\Gamma _*,\, \psi _*,\, P_*)$![]() .
.
Proof. From $(\Gamma + {\boldsymbol {k}}\beta )^{\dagger} =\Gamma ^{\dagger}$![]() we get $\Gamma \langle \beta \rangle =\Gamma +{\boldsymbol {k}}\beta$
we get $\Gamma \langle \beta \rangle =\Gamma +{\boldsymbol {k}}\beta$![]() . We have six cases:
. We have six cases:
Case 1: $(\Gamma ^{>})^{\dagger} < \eta < (\Gamma ^{>})'$![]() and $\eta \in P_1$
and $\eta \in P_1$![]() for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$
for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$![]() . Fix such $\eta$
. Fix such $\eta$![]() . Then $\Gamma$
. Then $\Gamma$![]() is dense in $\Gamma +{\boldsymbol {k}}\eta =\Gamma +{\boldsymbol {k}}\beta$
is dense in $\Gamma +{\boldsymbol {k}}\eta =\Gamma +{\boldsymbol {k}}\beta$![]() , by Corollary 2.4, so $[\Gamma +{\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}$
, by Corollary 2.4, so $[\Gamma +{\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}$![]() . Moreover, there is no $\eta _1\ne \eta$
. Moreover, there is no $\eta _1\ne \eta$![]() in $\Gamma +{\boldsymbol {k}}\beta$
in $\Gamma +{\boldsymbol {k}}\beta$![]() with $(\Gamma ^{>})^{\dagger} < \eta _1 < (\Gamma ^{>})'$
with $(\Gamma ^{>})^{\dagger} < \eta _1 < (\Gamma ^{>})'$![]() . By saturation, we can take $\eta _*\in \Gamma _*$
. By saturation, we can take $\eta _*\in \Gamma _*$![]() such that $(\Gamma ^{>})^{\dagger} < \eta _* < (\Gamma ^{>})'$
such that $(\Gamma ^{>})^{\dagger} < \eta _* < (\Gamma ^{>})'$![]() and $\eta _*\in P_*$
and $\eta _*\in P_*$![]() . Then [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$
. Then [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$![]() of ordered vector spaces over ${\boldsymbol {k}}$
of ordered vector spaces over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() with $i(\eta )=\eta _*$
with $i(\eta )=\eta _*$![]() . This $i$
. This $i$![]() embeds $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$
embeds $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$![]() into $(\Gamma _*,\, \psi _*,\, P_*)$
into $(\Gamma _*,\, \psi _*,\, P_*)$![]() .
.
Case 2: $(\Gamma ^{>})^{\dagger} < \eta < (\Gamma ^{>})'$![]() and $\eta \notin P_1$
and $\eta \notin P_1$![]() for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$
for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$![]() . Fixing such $\eta$
. Fixing such $\eta$![]() , we repeat the argument of Case 1, except that now $\eta _*\notin P_*$
, we repeat the argument of Case 1, except that now $\eta _*\notin P_*$![]() instead of $\eta _*\in P_*$
instead of $\eta _*\in P_*$![]() .
.
Case 3: $[\Gamma +{\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}$![]() , but there is no $\eta \in \Gamma +{\boldsymbol {k}}\beta$
, but there is no $\eta \in \Gamma +{\boldsymbol {k}}\beta$![]() with $(\Gamma ^{>})^{\dagger} < \eta < (\Gamma ^{>})'$
with $(\Gamma ^{>})^{\dagger} < \eta < (\Gamma ^{>})'$![]() . Then $P_{\beta }$
. Then $P_{\beta }$![]() is the only $H$
is the only $H$![]() -cut of $\Gamma \langle \beta \rangle$
-cut of $\Gamma \langle \beta \rangle$![]() . Saturation yields $\beta _*\in \Gamma _*$
. Saturation yields $\beta _*\in \Gamma _*$![]() realizing the same cut in $\Gamma$
realizing the same cut in $\Gamma$![]() as $\beta$
as $\beta$![]() . Then [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$
. Then [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$![]() of ordered vector spaces over ${\boldsymbol {k}}$
of ordered vector spaces over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() with $i(\beta )=\beta _*$
with $i(\beta )=\beta _*$![]() . For $\gamma \in \Gamma +{\boldsymbol {k}}\beta$
. For $\gamma \in \Gamma +{\boldsymbol {k}}\beta$![]() we have $[i(\gamma )]_{{\boldsymbol {k}}}=[\gamma ]_{{\boldsymbol {k}}}\in [\Gamma ]_{{\boldsymbol {k}}}$
we have $[i(\gamma )]_{{\boldsymbol {k}}}=[\gamma ]_{{\boldsymbol {k}}}\in [\Gamma ]_{{\boldsymbol {k}}}$![]() , so $i(\gamma )^{\dagger} =\gamma ^{\dagger} \in \Gamma ^{\dagger}$
, so $i(\gamma )^{\dagger} =\gamma ^{\dagger} \in \Gamma ^{\dagger}$![]() . Thus, $i$
. Thus, $i$![]() embeds $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$
embeds $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$![]() into $(\Gamma _*,\, \psi _*,\, P_*)$
into $(\Gamma _*,\, \psi _*,\, P_*)$![]() .
.
Assume next that we are not in Case 1, or Case 2, or Case 3. Then $[\Gamma + {\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}\ne [\Gamma ]_{{\boldsymbol {k}}}$![]() . Take $\gamma \in \Gamma \langle \beta \rangle \setminus \Gamma$
. Take $\gamma \in \Gamma \langle \beta \rangle \setminus \Gamma$![]() such that $\gamma >0$
such that $\gamma >0$![]() and $[\gamma ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
and $[\gamma ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() , so $[\Gamma \langle \beta \rangle ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\gamma ]_{{\boldsymbol {k}}}\big \}$
, so $[\Gamma \langle \beta \rangle ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}} \cup \big \{[\gamma ]_{{\boldsymbol {k}}}\big \}$![]() . We are not in Case 1 or Case 2, so $P_{\beta }$
. We are not in Case 1 or Case 2, so $P_{\beta }$![]() is the only $H$
is the only $H$![]() -cut of $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$
-cut of $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$![]() . Let $D$
. Let $D$![]() be the cut in $\Gamma$
be the cut in $\Gamma$![]() realized by $\gamma$
realized by $\gamma$![]() and $E:= \Gamma \setminus D$
and $E:= \Gamma \setminus D$![]() , so $D<\gamma < E$
, so $D<\gamma < E$![]() . Then $D$
. Then $D$![]() has no largest element, and so $D\cap \Gamma ^{>}\ne \emptyset$
has no largest element, and so $D\cap \Gamma ^{>}\ne \emptyset$![]() : if $d=\max D$
: if $d=\max D$![]() , then we have $0 <\gamma -d< \Gamma ^{>}$
, then we have $0 <\gamma -d< \Gamma ^{>}$![]() , and thus $(\Gamma ^{>})^{\dagger} < (\gamma -d)^{\dagger} < (\Gamma ^{>})'$
, and thus $(\Gamma ^{>})^{\dagger} < (\gamma -d)^{\dagger} < (\Gamma ^{>})'$![]() , contradicting that we are not in Case 1. Likewise, $E$
, contradicting that we are not in Case 1. Likewise, $E$![]() has no least element. Here are the remaining cases:
has no least element. Here are the remaining cases:
Case 4: $\gamma ^{\dagger} \in (D^{>0})^{\dagger} \cap E^{\dagger}$![]() . Saturation yields $\gamma _*\in \Gamma _*$
. Saturation yields $\gamma _*\in \Gamma _*$![]() realizing the same cut in $\Gamma$
realizing the same cut in $\Gamma$![]() as $\gamma$
as $\gamma$![]() . Then $\gamma _*^{\dagger} =\gamma ^{\dagger} \in (D^{>0})^{\dagger}$
. Then $\gamma _*^{\dagger} =\gamma ^{\dagger} \in (D^{>0})^{\dagger}$![]() , and [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$
, and [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$![]() of ordered vector spaces over ${\boldsymbol {k}}$
of ordered vector spaces over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() with $i(\gamma )=\gamma _*$
with $i(\gamma )=\gamma _*$![]() ; this $i$
; this $i$![]() embeds $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$
embeds $(\Gamma \langle \beta \rangle,\,\psi _{\beta },\, P_{\beta })$![]() into $(\Gamma _*,\, \psi _*,\, P_*)$
into $(\Gamma _*,\, \psi _*,\, P_*)$![]() .
.
Case 5: $\gamma ^{\dagger} \in (D^{>0})^{\dagger} > E^{\dagger}$![]() . Then saturation yields a $\gamma _*\in \Gamma _{*}$
. Then saturation yields a $\gamma _*\in \Gamma _{*}$![]() realizing the same cut in $\Gamma$
realizing the same cut in $\Gamma$![]() as $\gamma$
as $\gamma$![]() , with $\gamma _*^{\dagger} =\gamma ^{\dagger}$
, with $\gamma _*^{\dagger} =\gamma ^{\dagger}$![]() . By [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] this yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$
. By [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.16] this yields an embedding $i \colon \Gamma + {\boldsymbol {k}}\beta \to \Gamma _*$![]() of ordered vector spaces over ${\boldsymbol {k}}$
of ordered vector spaces over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() with $i(\gamma )=\gamma _*$
with $i(\gamma )=\gamma _*$![]() , and so as before $i$
, and so as before $i$![]() embeds $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta })$
embeds $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta })$![]() into $(\Gamma _*,\, \psi _*,\, P_*)$
into $(\Gamma _*,\, \psi _*,\, P_*)$![]() .
.
Case 6: $\gamma ^{\dagger} \in E^{\dagger} < (D^{>0})^{\dagger}$![]() . This is handled just like Case 5.
. This is handled just like Case 5.
Note that Cases 4, 5, 6 in the proof above do not occur if $(\Gamma _1,\,\psi _1)$![]() is of Hahn type.
is of Hahn type.
In view of Corollary 3.2 and Lemma 3.4, Theorem 3.3 reduces to:
Lemma 3.5 Suppose $(\Gamma,\,\psi )$![]() is closed and $(\Gamma + {\boldsymbol {k}}\gamma )^{\dagger} \ne \Gamma ^{\dagger}$
is closed and $(\Gamma + {\boldsymbol {k}}\gamma )^{\dagger} \ne \Gamma ^{\dagger}$![]() for all $\gamma \in \Gamma _1\setminus \Gamma$
for all $\gamma \in \Gamma _1\setminus \Gamma$![]() . Then $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta })$
. Then $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta })$![]() embeds into $(\Gamma _*,\, \psi _*,\, P_*)$
embeds into $(\Gamma _*,\, \psi _*,\, P_*)$![]() over $\Gamma$
over $\Gamma$![]() .
.
Proof. If $\gamma \in \Gamma _1\setminus \Gamma$![]() and $\Psi < \gamma < (\Gamma ^{>})'$
and $\Psi < \gamma < (\Gamma ^{>})'$![]() , then $(\Gamma + {\boldsymbol {k}}\gamma )^{\dagger} = \Gamma ^{\dagger}$
, then $(\Gamma + {\boldsymbol {k}}\gamma )^{\dagger} = \Gamma ^{\dagger}$![]() , contradicting our assumption. Hence there is no such $\gamma$
, contradicting our assumption. Hence there is no such $\gamma$![]() . It follows that $\Gamma ^{<}$
. It follows that $\Gamma ^{<}$![]() is cofinal in $\Gamma _1^{<}$
is cofinal in $\Gamma _1^{<}$![]() .
.
Take $\alpha _0\in \Gamma$![]() such that $(\beta -\alpha _0)^{\dagger} \notin \Gamma ^{\dagger}$
such that $(\beta -\alpha _0)^{\dagger} \notin \Gamma ^{\dagger}$![]() . Since $(\Gamma,\,\psi )$
. Since $(\Gamma,\,\psi )$![]() is closed, this means ${(\beta -\alpha _0)^{\dagger} \notin \Gamma }$
is closed, this means ${(\beta -\alpha _0)^{\dagger} \notin \Gamma }$![]() . Next take $\alpha _1\in \Gamma$
. Next take $\alpha _1\in \Gamma$![]() with $((\beta -\alpha _0)^{\dagger} -\alpha _1)^{\dagger} \notin \Gamma ^{\dagger}$
with $((\beta -\alpha _0)^{\dagger} -\alpha _1)^{\dagger} \notin \Gamma ^{\dagger}$![]() . Continuing this way, we obtain sequences $\alpha _0,\, \alpha _1,\, \alpha _2,\,\ldots$
. Continuing this way, we obtain sequences $\alpha _0,\, \alpha _1,\, \alpha _2,\,\ldots$![]() in $\Gamma$
in $\Gamma$![]() and $\beta _0,\, \beta _1,\, \beta _2,\,\ldots$
and $\beta _0,\, \beta _1,\, \beta _2,\,\ldots$![]() in $\Gamma \langle \beta \rangle \setminus \Gamma$
in $\Gamma \langle \beta \rangle \setminus \Gamma$![]() with
with
such that $\beta _n^{\dagger} \notin \Gamma$![]() for all $n$
for all $n$![]() . By Lemma 2.8 we have $\beta _0^{\dagger} < \beta _1^{\dagger} < \beta _2^{\dagger} < \cdots$
. By Lemma 2.8 we have $\beta _0^{\dagger} < \beta _1^{\dagger} < \beta _2^{\dagger} < \cdots$![]() . It follows that $[\beta _0]_{{\boldsymbol {k}}} >[\beta _1]_{{\boldsymbol {k}}} >[\beta _2]_{{\boldsymbol {k}}} > \cdots$
. It follows that $[\beta _0]_{{\boldsymbol {k}}} >[\beta _1]_{{\boldsymbol {k}}} >[\beta _2]_{{\boldsymbol {k}}} > \cdots$![]() , with $[\beta _n]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
, with $[\beta _n]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() for all $n$
for all $n$![]() . In particular, the family $(\beta _n)$
. In particular, the family $(\beta _n)$![]() is ${\boldsymbol {k}}$
is ${\boldsymbol {k}}$![]() -linearly independent over $\Gamma$
-linearly independent over $\Gamma$![]() , and
, and
By saturation we can take $\beta _*\in \Gamma _*\setminus \Gamma$![]() realizing the same cut in $\Gamma$
realizing the same cut in $\Gamma$![]() as $\beta$
as $\beta$![]() . This gives an embedding $e_0\colon \Gamma \oplus {\boldsymbol {k}} \beta \to \Gamma _*$
. This gives an embedding $e_0\colon \Gamma \oplus {\boldsymbol {k}} \beta \to \Gamma _*$![]() of ordered vector spaces over ${\boldsymbol {k}}$
of ordered vector spaces over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() and sends $\beta$
and sends $\beta$![]() to $\beta _*$
to $\beta _*$![]() . We define recursively $\beta _{*n}\in (\Gamma _*)_\infty$
. We define recursively $\beta _{*n}\in (\Gamma _*)_\infty$![]() by
by
Assume inductively that $\beta _{*0},\,\ldots,\,\beta _{*n}\in \Gamma _{*}$![]() and that we have an embedding
and that we have an embedding
of ordered vector spaces over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() and sends $\beta _i$
and sends $\beta _i$![]() to $\beta _{*i}$
to $\beta _{*i}$![]() for $i=0,\,\ldots,\,n$
for $i=0,\,\ldots,\,n$![]() . Then $\beta _n$
. Then $\beta _n$![]() and $\beta _{*n}$
and $\beta _{*n}$![]() realize the same cut in $\Gamma$
realize the same cut in $\Gamma$![]() , and so $\beta _{*n}^{\dagger} \notin \Gamma$
, and so $\beta _{*n}^{\dagger} \notin \Gamma$![]() , and $\beta _n^{\dagger}$
, and $\beta _n^{\dagger}$![]() and $\beta _{*n}^{\dagger}$
and $\beta _{*n}^{\dagger}$![]() realize the same cut in $\Gamma$
realize the same cut in $\Gamma$![]() by Lemma 2.7. Hence $\beta _{n+1}$
by Lemma 2.7. Hence $\beta _{n+1}$![]() and $\beta _{*(n+1)}\in \Gamma _*\setminus \Gamma$
and $\beta _{*(n+1)}\in \Gamma _*\setminus \Gamma$![]() realize the same cut in $\Gamma$
realize the same cut in $\Gamma$![]() . Moreover, $\beta ^{\dagger} _{*n} < \beta _{*(n+1)}^{\dagger}$
. Moreover, $\beta ^{\dagger} _{*n} < \beta _{*(n+1)}^{\dagger}$![]() by Lemma 2.8. We have
by Lemma 2.8. We have
Let $D$![]() be the cut realized by $[\beta _{n+1}]_{{\boldsymbol {k}}}$
be the cut realized by $[\beta _{n+1}]_{{\boldsymbol {k}}}$![]() in $[\Gamma +{\boldsymbol {k}}\beta _0+\cdots +{\boldsymbol {k}}\beta _n]_{{\boldsymbol {k}}}$
in $[\Gamma +{\boldsymbol {k}}\beta _0+\cdots +{\boldsymbol {k}}\beta _n]_{{\boldsymbol {k}}}$![]() . Then the above together with $[\beta _{*n}]_{{\boldsymbol {k}}} > [\beta _{*(n+1)}]_{{\boldsymbol {k}}}$
. Then the above together with $[\beta _{*n}]_{{\boldsymbol {k}}} > [\beta _{*(n+1)}]_{{\boldsymbol {k}}}$![]() shows that $[\beta _{*(n+1)}]_{{\boldsymbol {k}}}$
shows that $[\beta _{*(n+1)}]_{{\boldsymbol {k}}}$![]() realizes the $e_n$
realizes the $e_n$![]() -image of the cut $D$
-image of the cut $D$![]() in $[e_n(\Gamma +{\boldsymbol {k}}\beta _0+\cdots +{\boldsymbol {k}}\beta _n)]_{{\boldsymbol {k}}}$
in $[e_n(\Gamma +{\boldsymbol {k}}\beta _0+\cdots +{\boldsymbol {k}}\beta _n)]_{{\boldsymbol {k}}}$![]() . Hence $e_n$
. Hence $e_n$![]() extends to an embedding
extends to an embedding
of ordered vector spaces over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() and sends $\beta _{n+1}$
and sends $\beta _{n+1}$![]() to $\beta _{*(n+1)}$
to $\beta _{*(n+1)}$![]() . This leads to a map $e\colon \Gamma \langle \beta \rangle \to \Gamma _*$
. This leads to a map $e\colon \Gamma \langle \beta \rangle \to \Gamma _*$![]() that extends each $e_n$
that extends each $e_n$![]() , and is, therefore, an embedding of $H$
, and is, therefore, an embedding of $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() . Since $P_{\beta }$
. Since $P_{\beta }$![]() is the only $H$
is the only $H$![]() -cut in $\Gamma \langle \beta \rangle$
-cut in $\Gamma \langle \beta \rangle$![]() , $e$
, $e$![]() embeds $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta })$
embeds $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta })$![]() into $(\Gamma _*,\, \psi _*,\, P_*)$
into $(\Gamma _*,\, \psi _*,\, P_*)$![]() over $\Gamma$
over $\Gamma$![]() .
.
This concludes the proof of Theorem 3.3.
Let $T_{{\boldsymbol {k}}}$![]() be the $\mathcal {L}_{{\boldsymbol {k}}}$
be the $\mathcal {L}_{{\boldsymbol {k}}}$![]() -theory of closed $H$
-theory of closed $H$![]() -triples over ${\boldsymbol {k}}$
-triples over ${\boldsymbol {k}}$![]() . Let $T_{{\boldsymbol {k}}}^{>}$
. Let $T_{{\boldsymbol {k}}}^{>}$![]() be the $\mathcal {L}_{{\boldsymbol {k}}}$
be the $\mathcal {L}_{{\boldsymbol {k}}}$![]() -theory whose models are the closed $H$
-theory whose models are the closed $H$![]() -triples $(\Gamma,\,\psi,\, P)$
-triples $(\Gamma,\,\psi,\, P)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() with $0\in P$
with $0\in P$![]() , equivalently $\Psi \cap \Gamma ^{>}\ne \emptyset$
, equivalently $\Psi \cap \Gamma ^{>}\ne \emptyset$![]() . Let $T_{{\boldsymbol {k}}}^{<}$
. Let $T_{{\boldsymbol {k}}}^{<}$![]() be the $\mathcal {L}_{{\boldsymbol {k}}}$
be the $\mathcal {L}_{{\boldsymbol {k}}}$![]() -theory whose models are the closed $H$
-theory whose models are the closed $H$![]() -triples $(\Gamma,\,\psi,\, P)$
-triples $(\Gamma,\,\psi,\, P)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() with $0\notin P$
with $0\notin P$![]() , equivalently $\Psi \subseteq \Gamma ^{<}$
, equivalently $\Psi \subseteq \Gamma ^{<}$![]() .
.
Corollary 3.6 The $\mathcal {L}_{{\boldsymbol {k}}}$![]() -theory $T_{{\boldsymbol {k}}}$
-theory $T_{{\boldsymbol {k}}}$![]() has exactly two completions: $T_{{\boldsymbol {k}}}^{>}$
has exactly two completions: $T_{{\boldsymbol {k}}}^{>}$![]() and $T_{{\boldsymbol {k}}}^{<}$
and $T_{{\boldsymbol {k}}}^{<}$![]() .
.
Proof. We have an $H$![]() -triple $(\{0\},\,\psi _0,\, \{0\})$
-triple $(\{0\},\,\psi _0,\, \{0\})$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() that embeds into every model of $T_{{\boldsymbol {k}}}^{>}$
that embeds into every model of $T_{{\boldsymbol {k}}}^{>}$![]() , and an $H$
, and an $H$![]() -triple $(\{0\},\,\psi _0,\, \emptyset )$
-triple $(\{0\},\,\psi _0,\, \emptyset )$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() that embeds into every model of $T_{{\boldsymbol {k}}}^{<}$
that embeds into every model of $T_{{\boldsymbol {k}}}^{<}$![]() . Here $\psi _0$
. Here $\psi _0$![]() is the “empty” function $\emptyset \to \{0\}$
is the “empty” function $\emptyset \to \{0\}$![]() .
.
Suppose $K$![]() is a Liouville closed $H$
is a Liouville closed $H$![]() -field. Then its $H$
-field. Then its $H$![]() -couple $(\Gamma,\,\psi )$
-couple $(\Gamma,\,\psi )$![]() is naturally an $H$
is naturally an $H$![]() -couple over its constant field $C$
-couple over its constant field $C$![]() . The case $(\Gamma,\,\psi )\models T_{C}^{>}$
. The case $(\Gamma,\,\psi )\models T_{C}^{>}$![]() corresponds to the derivation $\partial$
corresponds to the derivation $\partial$![]() of $K$
of $K$![]() being small (that is, $\partial f \prec 1$
being small (that is, $\partial f \prec 1$![]() for all $f\prec 1$
for all $f\prec 1$![]() in $K$
in $K$![]() ), while the case $(\Gamma,\,\psi )\models T_{C}^{<}$
), while the case $(\Gamma,\,\psi )\models T_{C}^{<}$![]() corresponds to this derivation not being small. For example, the usual derivation $\frac {d}{dx}$
corresponds to this derivation not being small. For example, the usual derivation $\frac {d}{dx}$![]() of $\mathbb {T}$
of $\mathbb {T}$![]() is small. The derivation $x^2\frac {d}{dx}$
is small. The derivation $x^2\frac {d}{dx}$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() is not small, but $\mathbb {T}$
is not small, but $\mathbb {T}$![]() with this derivation is still Liouville closed.
with this derivation is still Liouville closed.
4. Simple extensions
Let $(\Gamma,\, \psi )$![]() be an $H$
be an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() with asymptotic integration, and let $(\Gamma ^*,\, \psi ^*)$
with asymptotic integration, and let $(\Gamma ^*,\, \psi ^*)$![]() be an $H$
be an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() that extends $(\Gamma,\, \psi )$
that extends $(\Gamma,\, \psi )$![]() . For $\gamma \in \Gamma ^*$
. For $\gamma \in \Gamma ^*$![]() , let $(\Gamma \langle \gamma \rangle,\,\psi _\gamma )$
, let $(\Gamma \langle \gamma \rangle,\,\psi _\gamma )$![]() denote the $H$
denote the $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() generated by $\Gamma \cup \{\gamma \}$
generated by $\Gamma \cup \{\gamma \}$![]() in $(\Gamma ^*,\, \psi ^*)$
in $(\Gamma ^*,\, \psi ^*)$![]() . Let $\beta \in \Gamma ^*\setminus \Gamma$
. Let $\beta \in \Gamma ^*\setminus \Gamma$![]() . The following result yields a useful description of the “simple” extension $(\Gamma \langle \beta \rangle,\,\psi _\beta )$
. The following result yields a useful description of the “simple” extension $(\Gamma \langle \beta \rangle,\,\psi _\beta )$![]() , where $i$
, where $i$![]() , $n$
, $n$![]() range over $\mathbb {N}=\{0,\,1,\,2,\,\ldots \}$
range over $\mathbb {N}=\{0,\,1,\,2,\,\ldots \}$![]() :
:
Proposition 4.1 One of the following occurs:
(a) $(\Gamma + {\boldsymbol {k}}\beta )^{\dagger} =\Gamma ^{\dagger} ;$

(b) there are sequences $(\alpha _i)$
 in $\Gamma$
in $\Gamma$ and $(\beta _i)$
and $(\beta _i)$ in $\Gamma ^*$
in $\Gamma ^*$ such that $(\beta _i)$
such that $(\beta _i)$ is ${\boldsymbol {k}}$
is ${\boldsymbol {k}}$ -linearly independent over $\Gamma,$
-linearly independent over $\Gamma,$ $\beta _0=\beta -\alpha _0$
$\beta _0=\beta -\alpha _0$ and $\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$
and $\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$ for all $i$
for all $i$ , and such that $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^\infty {\boldsymbol {k}}\beta _i$
, and such that $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^\infty {\boldsymbol {k}}\beta _i$ .
.(c) n there are $\alpha _0,\,\ldots,\,\alpha _n\in \Gamma,$
 and non-zero $\beta _0,\,\ldots,\, \beta _n\in \Gamma ^*$
and non-zero $\beta _0,\,\ldots,\, \beta _n\in \Gamma ^*$ such that $\beta _0=\beta -\alpha _0,$
such that $\beta _0=\beta -\alpha _0,$ $\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$
$\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$ for $i< n,$
for $i< n,$ the vectors $\beta _0,\,\ldots,\, \beta _n,\, \beta _n^{\dagger}$
the vectors $\beta _0,\,\ldots,\, \beta _n,\, \beta _n^{\dagger}$ are ${\boldsymbol {k}}$
are ${\boldsymbol {k}}$ -linearly independent over $\Gamma,$
-linearly independent over $\Gamma,$ $(\Gamma +{\boldsymbol {k}}\beta _n^{\dagger} )^{\dagger} =\Gamma ^{\dagger},$
$(\Gamma +{\boldsymbol {k}}\beta _n^{\dagger} )^{\dagger} =\Gamma ^{\dagger},$ and $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^n {\boldsymbol {k}}\beta _i \oplus {\boldsymbol {k}}\beta _n^{\dagger}$
and $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^n {\boldsymbol {k}}\beta _i \oplus {\boldsymbol {k}}\beta _n^{\dagger}$ .
.(d) n there are $\alpha _0,\,\ldots,\,\alpha _n\in \Gamma,$
 and non-zero $\beta _0,\,\ldots,\, \beta _n\in \Gamma ^*$
and non-zero $\beta _0,\,\ldots,\, \beta _n\in \Gamma ^*$ such that $\beta _0=\beta -\alpha _0,$
such that $\beta _0=\beta -\alpha _0,$ $\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$
$\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$ for $i< n,$
for $i< n,$ the vectors $\beta _0,\,\ldots,\, \beta _n$
the vectors $\beta _0,\,\ldots,\, \beta _n$ are ${\boldsymbol {k}}$
are ${\boldsymbol {k}}$ -linearly independent over $\Gamma,$
-linearly independent over $\Gamma,$ $\beta _n^{\dagger} \in \Gamma \setminus \Gamma ^{\dagger},$
$\beta _n^{\dagger} \in \Gamma \setminus \Gamma ^{\dagger},$ and $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^n {\boldsymbol {k}}\beta _i$
and $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^n {\boldsymbol {k}}\beta _i$ .
.
Note that in case (a) we have $\Gamma \langle \beta \rangle =\Gamma \oplus {\boldsymbol {k}}\beta$![]() , a case described in more detail in Lemma 3.4. The proof below gives extra information about the other cases.
, a case described in more detail in Lemma 3.4. The proof below gives extra information about the other cases.
Proof. Suppose we are not in case (a). Then we have $\alpha _0\in \Gamma$![]() and $\beta _0:=\beta -\alpha _0$
and $\beta _0:=\beta -\alpha _0$![]() with $\beta _0^{\dagger} \notin \Gamma ^{\dagger}$
with $\beta _0^{\dagger} \notin \Gamma ^{\dagger}$![]() . This is the first step in inductively constructing elements $\alpha _i\in \Gamma$
. This is the first step in inductively constructing elements $\alpha _i\in \Gamma$![]() and $\beta _i\in \Gamma \langle \beta \rangle \setminus \Gamma _0$
and $\beta _i\in \Gamma \langle \beta \rangle \setminus \Gamma _0$![]() , either for all $i$
, either for all $i$![]() , or for all $i\leqslant n$
, or for all $i\leqslant n$![]() for a certain $n$
for a certain $n$![]() . Suppose we already have $\alpha _0,\,\ldots,\, \alpha _n\in \Gamma$
. Suppose we already have $\alpha _0,\,\ldots,\, \alpha _n\in \Gamma$![]() and $\beta _0,\,\ldots,\, \beta _n\in \Gamma \langle \beta \rangle \setminus \Gamma$
and $\beta _0,\,\ldots,\, \beta _n\in \Gamma \langle \beta \rangle \setminus \Gamma$![]() with $\alpha _0$
with $\alpha _0$![]() and $\beta _0$
and $\beta _0$![]() as above, $\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$
as above, $\beta _{i+1}=\beta _i^{\dagger} -\alpha _{i+1}$![]() and $\beta _i^{\dagger} \notin \Gamma$
and $\beta _i^{\dagger} \notin \Gamma$![]() for $i < n$
for $i < n$![]() , and $\beta _n^{\dagger} \notin \Gamma ^{\dagger}$
, and $\beta _n^{\dagger} \notin \Gamma ^{\dagger}$![]() . Thus, $[\beta _i]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
. Thus, $[\beta _i]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() for $i\leqslant n$
for $i\leqslant n$![]() .
.
Claim 1: $\beta _0^{\dagger} < \cdots < \beta _n^{\dagger}$![]() .
.
Claim 2: there is no $\eta \in \Gamma + {\boldsymbol {k}} \beta _0+ \cdots + {\boldsymbol {k}} \beta _n$![]() with $\Psi < \eta < (\Gamma ^{>})'$
with $\Psi < \eta < (\Gamma ^{>})'$![]() .
.
To prove Claim 1, assume towards a contradiction that $\beta _i^{\dagger} \geqslant \beta _{i+1}^{\dagger}$![]() , $i< n$
, $i< n$![]() . Then by Lemma 2.8 we have $0<|\beta _i|<\Gamma ^{>}$
. Then by Lemma 2.8 we have $0<|\beta _i|<\Gamma ^{>}$![]() , so $\Psi < \beta _i^{\dagger} < (\Gamma ^{>})'$
, so $\Psi < \beta _i^{\dagger} < (\Gamma ^{>})'$![]() , and thus $[\beta _{i+1}]_{{\boldsymbol {k}}}\in [\Gamma ]_{{\boldsymbol {k}}}$
, and thus $[\beta _{i+1}]_{{\boldsymbol {k}}}\in [\Gamma ]_{{\boldsymbol {k}}}$![]() by Corollary 2.4, a contradiction. It follows from Claim 1 that $[\beta _0]_{{\boldsymbol {k}}} > \cdots > [\beta _n]_{{\boldsymbol {k}}}$
by Corollary 2.4, a contradiction. It follows from Claim 1 that $[\beta _0]_{{\boldsymbol {k}}} > \cdots > [\beta _n]_{{\boldsymbol {k}}}$![]() and that $\beta _0,\,\ldots,\, \beta _n$
and that $\beta _0,\,\ldots,\, \beta _n$![]() are ${\boldsymbol {k}}$
are ${\boldsymbol {k}}$![]() -linearly independent over $\Gamma$
-linearly independent over $\Gamma$![]() . As to Claim 2, suppose towards a contradiction that $\Psi < \gamma + \delta < (\Gamma ^{>})'$
. As to Claim 2, suppose towards a contradiction that $\Psi < \gamma + \delta < (\Gamma ^{>})'$![]() where $\gamma \in \Gamma$
where $\gamma \in \Gamma$![]() , $\delta \in {\boldsymbol {k}}\beta _0+\cdots + {\boldsymbol {k}}\beta _n$
, $\delta \in {\boldsymbol {k}}\beta _0+\cdots + {\boldsymbol {k}}\beta _n$![]() . Then $\delta \ne 0$
. Then $\delta \ne 0$![]() , and so $[\delta ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
, and so $[\delta ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() . With $D:= \Psi -\gamma$
. With $D:= \Psi -\gamma$![]() and $E:=(\Gamma ^{>})'-\gamma$
and $E:=(\Gamma ^{>})'-\gamma$![]() , we have $D < \delta < E$
, we have $D < \delta < E$![]() . On the other hand, for every $\varepsilon \in \Gamma ^{>}$
. On the other hand, for every $\varepsilon \in \Gamma ^{>}$![]() there are $d\in D$
there are $d\in D$![]() and $e\in E$
and $e\in E$![]() with $e-d<\varepsilon$
with $e-d<\varepsilon$![]() , so $\Gamma$
, so $\Gamma$![]() is dense in $\Gamma +{\boldsymbol {k}}\delta$
is dense in $\Gamma +{\boldsymbol {k}}\delta$![]() by [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.17], contradicting $[\delta ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
by [Reference Aschenbrenner, van den Dries and van der Hoeven2, 2.4.17], contradicting $[\delta ]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() . This concludes the proof of Claim 2.
. This concludes the proof of Claim 2.
If $(\beta _n^{\dagger} -\alpha _{n+1})^{\dagger} \notin \Gamma ^{\dagger}$![]() for some $\alpha _{n+1}\in \Gamma$
for some $\alpha _{n+1}\in \Gamma$![]() (so $\beta _n^{\dagger} \notin \Gamma$
(so $\beta _n^{\dagger} \notin \Gamma$![]() ), then we take such an $\alpha _{n+1}$
), then we take such an $\alpha _{n+1}$![]() and set $\beta _{n+1}:=\beta _n^{\dagger} -\alpha _{n+1}$
and set $\beta _{n+1}:=\beta _n^{\dagger} -\alpha _{n+1}$![]() . If there is no such $\alpha _{n+1}$
. If there is no such $\alpha _{n+1}$![]() , then the construction breaks off, with $\alpha _n$
, then the construction breaks off, with $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() as the last vectors.
as the last vectors.
Suppose the construction goes on indefinitely. Then it yields infinite sequences $(\alpha _i)$![]() and $(\beta _i)$
and $(\beta _i)$![]() as in case (b), in particular, $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^\infty {\boldsymbol {k}}\beta _i$
as in case (b), in particular, $\Gamma \langle \beta \rangle =\Gamma \oplus \bigoplus _{i=0}^\infty {\boldsymbol {k}}\beta _i$![]() ,
,
and $(\Gamma \langle \beta \rangle,\, \psi _\beta )$![]() has asymptotic integration by Claim 2.
has asymptotic integration by Claim 2.
Next, assume that the construction stops with $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() as the last vectors. Thus, $({\Gamma +{\boldsymbol {k}}\beta _n^{\dagger} })^{\dagger} =\Gamma ^{\dagger}$
as the last vectors. Thus, $({\Gamma +{\boldsymbol {k}}\beta _n^{\dagger} })^{\dagger} =\Gamma ^{\dagger}$![]() . We have two cases:
. We have two cases:
Case 1: $\beta _n^{\dagger} \notin \Gamma$![]() . Then $\alpha _0,\,\ldots,\, \alpha _n,\, \beta _0,\,\ldots,\, \beta _n$
. Then $\alpha _0,\,\ldots,\, \alpha _n,\, \beta _0,\,\ldots,\, \beta _n$![]() are as in case (c)$_n$
are as in case (c)$_n$![]() . Here is why. Set $\Delta :=\Gamma + {\boldsymbol {k}}\beta _n^{\dagger}$
. Here is why. Set $\Delta :=\Gamma + {\boldsymbol {k}}\beta _n^{\dagger}$![]() , so $\Delta ^{{\dagger} }=\Gamma ^{\dagger}$
, so $\Delta ^{{\dagger} }=\Gamma ^{\dagger}$![]() . From $\beta _i^{\dagger} \notin \Delta ^{\dagger}$
. From $\beta _i^{\dagger} \notin \Delta ^{\dagger}$![]() for all $i\leqslant n$
for all $i\leqslant n$![]() and Claim 1 we obtain that $\beta _0,\,\ldots,\, \beta _n$
and Claim 1 we obtain that $\beta _0,\,\ldots,\, \beta _n$![]() are ${\boldsymbol {k}}$
are ${\boldsymbol {k}}$![]() -linearly independent over $\Delta$
-linearly independent over $\Delta$![]() , with
, with
and $\beta \in \Delta + {\boldsymbol {k}}\beta _0$![]() , which proves the assertion.
, which proves the assertion.
Case 2: $\beta _n^{\dagger} \in \Gamma$![]() . Then $\alpha _0,\,\ldots,\, \alpha _n,\, \beta _0,\,\ldots,\, \beta _n$
. Then $\alpha _0,\,\ldots,\, \alpha _n,\, \beta _0,\,\ldots,\, \beta _n$![]() are as in case (d)$_n$
are as in case (d)$_n$![]() . Here is why. From $\beta _i^{\dagger} \notin \Gamma ^{\dagger}$
. Here is why. From $\beta _i^{\dagger} \notin \Gamma ^{\dagger}$![]() for all $i\leqslant n$
for all $i\leqslant n$![]() and Claim 1 we obtain that $\beta _0,\,\ldots,\, \beta _n$
and Claim 1 we obtain that $\beta _0,\,\ldots,\, \beta _n$![]() are ${\boldsymbol {k}}$
are ${\boldsymbol {k}}$![]() -linearly independent over $\Gamma$
-linearly independent over $\Gamma$![]() , with
, with
and $\beta \in \Gamma + {\boldsymbol {k}}\beta _0$![]() , which proves the assertion.
, which proves the assertion.
In case (d)$_n$![]() we have $\beta _n^{\dagger} \in \Gamma \setminus \Gamma ^{\dagger}$
we have $\beta _n^{\dagger} \in \Gamma \setminus \Gamma ^{\dagger}$![]() , and this cannot happen if $(\Gamma,\,\psi )$
, and this cannot happen if $(\Gamma,\,\psi )$![]() is closed. The proof of Proposition 4.1 yields some further results that are needed later:
is closed. The proof of Proposition 4.1 yields some further results that are needed later:
Lemma 4.2 Let $(\alpha _i)$![]() and $(\beta _i)$
and $(\beta _i)$![]() be as in ${\rm (b)}$
be as in ${\rm (b)}$![]() . Then:
. Then:
(i) $\beta _i^{\dagger} \notin \Gamma$
 for all $i,$
for all $i,$ and thus $[\beta _i]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
and thus $[\beta _i]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$ for all $i;$
for all $i;$
(ii) $(\beta _i^{\dagger} )$
 is strictly increasing, and thus $([\beta _i]_{{\boldsymbol {k}}})$
is strictly increasing, and thus $([\beta _i]_{{\boldsymbol {k}}})$ is strictly decreasing;
is strictly decreasing;(iii) $[\Gamma \langle \beta \rangle ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}\cup \big \{[\beta _i]_{{\boldsymbol {k}}}:\,i\in \mathbb {N}\big \},$
 and thus $\Psi _{\beta } = \Psi \cup \big \{\beta _i^{\dagger} :\, i\in \mathbb {N}\big \};$
and thus $\Psi _{\beta } = \Psi \cup \big \{\beta _i^{\dagger} :\, i\in \mathbb {N}\big \};$
(iv) there is no $\eta \in \Gamma \langle \beta \rangle$
 with $\Psi < \eta < (\Gamma ^{>})';$
with $\Psi < \eta < (\Gamma ^{>})';$
(v) $(\Gamma \langle \beta \rangle,\, \psi _\beta )$
 has asymptotic integration;
has asymptotic integration;(vi) $\Gamma ^{<}$
 is cofinal in $\Gamma \langle \beta \rangle ^{<}$
is cofinal in $\Gamma \langle \beta \rangle ^{<}$ .
.
If $(\Gamma,\, \psi )$![]() is closed and $\gamma \in \Gamma ^*\setminus \Gamma$
is closed and $\gamma \in \Gamma ^*\setminus \Gamma$![]() realizes the same cut in $\Gamma$
realizes the same cut in $\Gamma$![]() as $\beta$
as $\beta$![]() , then we have an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta })\to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma })$
, then we have an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta })\to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma })$![]() of $H$
of $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() and sends $\beta$
and sends $\beta$![]() to $\gamma$
to $\gamma$![]() . If $(\Gamma,\, \psi )$
. If $(\Gamma,\, \psi )$![]() is of Hahn type, then so is $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$
is of Hahn type, then so is $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$![]() .
.
Proof. As to (i), this follows from the ${\boldsymbol {k}}$![]() -linear independence of $(\beta _i)$
-linear independence of $(\beta _i)$![]() over $\Gamma$
over $\Gamma$![]() and from $\beta _{i}^{\dagger} =\beta _{i+1}+\alpha _{i+1}$
and from $\beta _{i}^{\dagger} =\beta _{i+1}+\alpha _{i+1}$![]() . Hence the sequences $(\alpha _i),$
. Hence the sequences $(\alpha _i),$![]() and $(\beta _i)$
and $(\beta _i)$![]() conform to the construction in the proof of Proposition 4.1, and so other parts of that proof yield (ii)–(vi). The next statement follows as in the proof of Lemma 3.5 using Lemma 2.7 and (iv).
conform to the construction in the proof of Proposition 4.1, and so other parts of that proof yield (ii)–(vi). The next statement follows as in the proof of Lemma 3.5 using Lemma 2.7 and (iv).
Suppose that $(\Gamma,\,\psi )$![]() is of Hahn type. We show that then $\Gamma \langle \beta \rangle$
is of Hahn type. We show that then $\Gamma \langle \beta \rangle$![]() is a Hahn space; the additional argument required for showing that $(\Gamma \langle \beta \rangle,\,\psi _{\beta })$
is a Hahn space; the additional argument required for showing that $(\Gamma \langle \beta \rangle,\,\psi _{\beta })$![]() is of Hahn type is similar and left to the reader. So let $\delta _1,\, \delta _2\in \Gamma \langle \beta \rangle ^{\ne }$
is of Hahn type is similar and left to the reader. So let $\delta _1,\, \delta _2\in \Gamma \langle \beta \rangle ^{\ne }$![]() satisfy $[\delta _1]_{{\boldsymbol {k}}}=[\delta _2]_{{\boldsymbol {k}}}$
satisfy $[\delta _1]_{{\boldsymbol {k}}}=[\delta _2]_{{\boldsymbol {k}}}$![]() ; we have to find $c\in {\boldsymbol {k}}$
; we have to find $c\in {\boldsymbol {k}}$![]() such that $[\delta _1-c\delta _2]_{{\boldsymbol {k}}}< [\delta _1]_{{\boldsymbol {k}}}$
such that $[\delta _1-c\delta _2]_{{\boldsymbol {k}}}< [\delta _1]_{{\boldsymbol {k}}}$![]() . Now
. Now
with all $c_{i1},\, c_{i2}\in {\boldsymbol {k}}$![]() , and $c_{i1}=c_{i2}=0$
, and $c_{i1}=c_{i2}=0$![]() for all but finitely many $i$
for all but finitely many $i$![]() . Consider first the case $[\delta _1]_{{\boldsymbol {k}}}\in [\Gamma ]_{{\boldsymbol {k}}}$
. Consider first the case $[\delta _1]_{{\boldsymbol {k}}}\in [\Gamma ]_{{\boldsymbol {k}}}$![]() . Then $[\gamma _1]_{{\boldsymbol {k}}}> [\beta _i]_{{\boldsymbol {k}}}$
. Then $[\gamma _1]_{{\boldsymbol {k}}}> [\beta _i]_{{\boldsymbol {k}}}$![]() for all $i$
for all $i$![]() with $c_{i1}\ne 0$
with $c_{i1}\ne 0$![]() , by (i), (ii), (iii), and so $\delta _1=\gamma _1+ \alpha _1$
, by (i), (ii), (iii), and so $\delta _1=\gamma _1+ \alpha _1$![]() with $[\alpha _1]_{{\boldsymbol {k}}}< [\gamma _1]_{{\boldsymbol {k}}}=[\delta _1]_{{\boldsymbol {k}}}$
with $[\alpha _1]_{{\boldsymbol {k}}}< [\gamma _1]_{{\boldsymbol {k}}}=[\delta _1]_{{\boldsymbol {k}}}$![]() , and likewise $\delta _2=\gamma _2 + \alpha _2$
, and likewise $\delta _2=\gamma _2 + \alpha _2$![]() with $[\alpha _2]_{{\boldsymbol {k}}}< [\gamma _2]_{{\boldsymbol {k}}}=[\delta _2]_{{\boldsymbol {k}}}$
with $[\alpha _2]_{{\boldsymbol {k}}}< [\gamma _2]_{{\boldsymbol {k}}}=[\delta _2]_{{\boldsymbol {k}}}$![]() . Take $c\in {\boldsymbol {k}}$
. Take $c\in {\boldsymbol {k}}$![]() such that $[\gamma _1-c\gamma _2]_{{\boldsymbol {k}}}<[\gamma _1]_{{\boldsymbol {k}}}$
such that $[\gamma _1-c\gamma _2]_{{\boldsymbol {k}}}<[\gamma _1]_{{\boldsymbol {k}}}$![]() . Then $\delta _1-c\delta _2= \gamma _1-c\gamma _2+ \alpha _1-c\alpha _2$
. Then $\delta _1-c\delta _2= \gamma _1-c\gamma _2+ \alpha _1-c\alpha _2$![]() , so $[\delta _1-c\delta _2]_{{\boldsymbol {k}}}<[\gamma _1]_{{\boldsymbol {k}}}=[\delta _1]_{{\boldsymbol {k}}}$
, so $[\delta _1-c\delta _2]_{{\boldsymbol {k}}}<[\gamma _1]_{{\boldsymbol {k}}}=[\delta _1]_{{\boldsymbol {k}}}$![]() . Next, suppose $[\delta _1]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$
. Next, suppose $[\delta _1]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}}$![]() . Then $c_{i1}\ne 0$
. Then $c_{i1}\ne 0$![]() for some $i$
for some $i$![]() ; let $j$
; let $j$![]() be the least such $i$
be the least such $i$![]() . Then $[\gamma _1]_{{\boldsymbol {k}}}<[\beta _j]_{{\boldsymbol {k}}}$
. Then $[\gamma _1]_{{\boldsymbol {k}}}<[\beta _j]_{{\boldsymbol {k}}}$![]() and $[\delta _1]_{{\boldsymbol {k}}}=[\beta _j]_{{\boldsymbol {k}}}$
and $[\delta _1]_{{\boldsymbol {k}}}=[\beta _j]_{{\boldsymbol {k}}}$![]() by (ii). Now $j$
by (ii). Now $j$![]() is also the least $i$
is also the least $i$![]() with $c_{i2}\ne 0$
with $c_{i2}\ne 0$![]() , in view of $[\delta _1]_{{\boldsymbol {k}}}=[\delta _2]_{{\boldsymbol {k}}}$
, in view of $[\delta _1]_{{\boldsymbol {k}}}=[\delta _2]_{{\boldsymbol {k}}}$![]() . Then $[\delta _1-c\delta _2]_{{\boldsymbol {k}}}<[\delta _1]_{{\boldsymbol {k}}}$
. Then $[\delta _1-c\delta _2]_{{\boldsymbol {k}}}<[\delta _1]_{{\boldsymbol {k}}}$![]() for $c\in {\boldsymbol {k}}$
for $c\in {\boldsymbol {k}}$![]() with $c_{j1}=cc_{j2}$
with $c_{j1}=cc_{j2}$![]() .
.
Lemma 4.3 Let $\alpha _0,\,\ldots,\, \alpha _n,\, \beta _1,\,\ldots,\, \beta _n$![]() be as in (c)$_n$
be as in (c)$_n$![]() , and set $\Delta :=\Gamma +{\boldsymbol {k}}\beta _n^{\dagger},$
, and set $\Delta :=\Gamma +{\boldsymbol {k}}\beta _n^{\dagger},$![]() so $\Delta ^{\dagger} =\Gamma ^{\dagger}$
so $\Delta ^{\dagger} =\Gamma ^{\dagger}$![]() and $\Gamma \langle \beta \rangle =\Delta \oplus {\boldsymbol {k}}\beta _0\oplus \cdots \oplus {\boldsymbol {k}}\beta _n$
and $\Gamma \langle \beta \rangle =\Delta \oplus {\boldsymbol {k}}\beta _0\oplus \cdots \oplus {\boldsymbol {k}}\beta _n$![]() . Then:
. Then:
(i) $\Gamma ^{<}$
 is cofinal in $\Delta ^{<};$
is cofinal in $\Delta ^{<};$
(ii) $\beta _0^{\dagger},\, \ldots,\, \beta _{n}^{\dagger} \notin \Gamma,$
 , and thus $[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\notin [\Delta ]_{{\boldsymbol {k}}};$
, and thus $[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\notin [\Delta ]_{{\boldsymbol {k}}};$
(iii) $\beta _0^{\dagger} < \cdots < \beta _n^{\dagger},$
 and thus $[\beta _0]_{{\boldsymbol {k}}}> \cdots > [\beta _n]_{{\boldsymbol {k}}};$
and thus $[\beta _0]_{{\boldsymbol {k}}}> \cdots > [\beta _n]_{{\boldsymbol {k}}};$
(iv) $\Psi _{\beta } = \Psi \cup \{\beta _0^{\dagger},\,\ldots,\, \beta _n^{\dagger} \}$
 and $[\Gamma \langle \beta \rangle ]_{{\boldsymbol {k}}}=[\Delta ]_{{\boldsymbol {k}}}\cup \big \{[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\big \};$
and $[\Gamma \langle \beta \rangle ]_{{\boldsymbol {k}}}=[\Delta ]_{{\boldsymbol {k}}}\cup \big \{[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\big \};$
(v) there is no $\gamma \in \Delta + {\boldsymbol {k}}\beta _0+\cdots + {\boldsymbol {k}}\beta _{n-1}$
 with $0 < \gamma < \Gamma ^{>};$
with $0 < \gamma < \Gamma ^{>};$
(vi) if $|\beta _n|\geqslant \alpha$
 for some $\alpha \in \Gamma ^{>},$
for some $\alpha \in \Gamma ^{>},$ then $\Gamma ^{<}$
then $\Gamma ^{<}$ is cofinal in $\Gamma \langle \beta \rangle ^{<}$
is cofinal in $\Gamma \langle \beta \rangle ^{<}$ and so a gap in $(\Delta,\, \psi _{\Delta }),$
and so a gap in $(\Delta,\, \psi _{\Delta }),$ if any, remains a gap in $(\Gamma \langle \beta \rangle,\, \psi _{\beta });$
if any, remains a gap in $(\Gamma \langle \beta \rangle,\, \psi _{\beta });$
(vii) if $|\beta _n|< \Gamma ^{>},$
 then $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$
then $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$ is grounded with $\max \Psi _{\beta }=\beta _n^{\dagger} ;$
is grounded with $\max \Psi _{\beta }=\beta _n^{\dagger} ;$
(viii) if $(\Delta,\, \psi _{\Delta })$
 has no gap, then there is no $\eta \in \Gamma \langle \beta \rangle$
has no gap, then there is no $\eta \in \Gamma \langle \beta \rangle$ with $\Psi < \eta < (\Gamma ^{>})'$
with $\Psi < \eta < (\Gamma ^{>})'$ , and so $\Gamma ^{<}$
, and so $\Gamma ^{<}$ is cofinal in $\Gamma \langle \beta \rangle ^{<}$
is cofinal in $\Gamma \langle \beta \rangle ^{<}$ and $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$
and $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$ has asymptotic integration.
has asymptotic integration.
Proof. As to (i), if $\delta \in \Delta$![]() and $\Gamma ^{<}< \delta < 0$
and $\Gamma ^{<}< \delta < 0$![]() , then $\Psi < \delta ^{\dagger}$
, then $\Psi < \delta ^{\dagger}$![]() , contradicting $\Delta ^{\dagger} =\Gamma ^{\dagger}$
, contradicting $\Delta ^{\dagger} =\Gamma ^{\dagger}$![]() . Item (ii) follows from the ${\boldsymbol {k}}$
. Item (ii) follows from the ${\boldsymbol {k}}$![]() -linear independence of $\beta _0,\,\ldots,\, \beta _n,\, \beta _n^{\dagger}$
-linear independence of $\beta _0,\,\ldots,\, \beta _n,\, \beta _n^{\dagger}$![]() over $\Gamma$
over $\Gamma$![]() and from $\beta _{i}^{\dagger} =\beta _{i+1}+\alpha _{i+1}$
and from $\beta _{i}^{\dagger} =\beta _{i+1}+\alpha _{i+1}$![]() for $i < n$
for $i < n$![]() . Next, we obtain (iii) from Claim 1 in the proof of Proposition 4.1, and then (iv) follows easily. As to (v), by (ii) and (iii) we have
. Next, we obtain (iii) from Claim 1 in the proof of Proposition 4.1, and then (iv) follows easily. As to (v), by (ii) and (iii) we have
Thus, assuming towards a contradiction that (v) is false gives $\gamma \in \Delta \cup \{\beta _0,\,\ldots,\, \beta _{n-1}\}$![]() with $0 < |\gamma | < \Gamma ^{>}$
with $0 < |\gamma | < \Gamma ^{>}$![]() . Then $\Psi <\gamma ^{\dagger} < (\Gamma ^{>})'$
. Then $\Psi <\gamma ^{\dagger} < (\Gamma ^{>})'$![]() , and so $\gamma \notin \Delta$
, and so $\gamma \notin \Delta$![]() . Hence $\gamma =\beta _i$
. Hence $\gamma =\beta _i$![]() with $i < n$
with $i < n$![]() , and so $\gamma ^{\dagger} \in \Gamma +{\boldsymbol {k}}\beta _0+ \cdots + {\boldsymbol {k}}\beta _n$
, and so $\gamma ^{\dagger} \in \Gamma +{\boldsymbol {k}}\beta _0+ \cdots + {\boldsymbol {k}}\beta _n$![]() , contradicting Claim 2 in the proof of Proposition 4.1 with $\gamma ^{\dagger}$
, contradicting Claim 2 in the proof of Proposition 4.1 with $\gamma ^{\dagger}$![]() in the role of $\eta$
in the role of $\eta$![]() . By similar arguments, if $0 < \gamma < \Gamma ^{>}$
. By similar arguments, if $0 < \gamma < \Gamma ^{>}$![]() for some $\gamma \in \Gamma \langle \beta \rangle$
for some $\gamma \in \Gamma \langle \beta \rangle$![]() , then $0 < |\beta _n| < \Gamma ^{>}$
, then $0 < |\beta _n| < \Gamma ^{>}$![]() . This gives (vi). For (vii), assume $|\beta _n|< \Gamma ^{>}$
. This gives (vi). For (vii), assume $|\beta _n|< \Gamma ^{>}$![]() . Then (i), (iv), (v) give $[\beta _n]_{{\boldsymbol {k}}}=\min \![\Gamma \langle \beta \rangle ^{\ne }]_{{\boldsymbol {k}}}$
. Then (i), (iv), (v) give $[\beta _n]_{{\boldsymbol {k}}}=\min \![\Gamma \langle \beta \rangle ^{\ne }]_{{\boldsymbol {k}}}$![]() , and thus $\max \Psi _\beta =\beta _n^{\dagger}$
, and thus $\max \Psi _\beta =\beta _n^{\dagger}$![]() .
.
As to (viii), note first that $\Psi =\Psi _{\Delta }$![]() . Assume $(\Delta,\, \psi _{\Delta })$
. Assume $(\Delta,\, \psi _{\Delta })$![]() has no gap. Then $(\Delta,\, \psi _{\Delta })$
has no gap. Then $(\Delta,\, \psi _{\Delta })$![]() has asymptotic integration. Hence by Claim 2 in the proof of Proposition 4.1, applied to $\Delta$
has asymptotic integration. Hence by Claim 2 in the proof of Proposition 4.1, applied to $\Delta$![]() instead of $\Gamma$
instead of $\Gamma$![]() , there is no $\eta \in \Gamma \langle \beta \rangle$
, there is no $\eta \in \Gamma \langle \beta \rangle$![]() with $\Psi < \eta < (\Gamma ^{>})'$
with $\Psi < \eta < (\Gamma ^{>})'$![]() .
.
Lemma 4.4 Let $\alpha _0,\,\ldots,\, \alpha _n,\, \beta _0,\,\ldots,\, \beta _n$![]() be as in (d)$_n$
be as in (d)$_n$![]() . Then:
. Then:
(i) $\beta _0^{\dagger},\, \ldots,\, \beta _{n-1}^{\dagger} \notin \Gamma,$
 $\beta _n^{\dagger} \notin \Psi,$
$\beta _n^{\dagger} \notin \Psi,$ and thus $[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}};$
and thus $[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\notin [\Gamma ]_{{\boldsymbol {k}}};$
(ii) $\beta _0^{\dagger} < \cdots < \beta _n^{\dagger},$
 and thus $[\beta _0]_{{\boldsymbol {k}}}> \cdots > [\beta _n]_{{\boldsymbol {k}}};$
and thus $[\beta _0]_{{\boldsymbol {k}}}> \cdots > [\beta _n]_{{\boldsymbol {k}}};$
(iii) $\Psi _{\beta } = \Psi \cup \{\beta _0^{\dagger},\,\ldots,\, \beta _n^{\dagger} \}$
 and $[\Gamma \langle \beta \rangle ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}\cup \big \{[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\big \};$
and $[\Gamma \langle \beta \rangle ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}\cup \big \{[\beta _0]_{{\boldsymbol {k}}},\,\ldots,\,[\beta _n]_{{\boldsymbol {k}}}\big \};$
(iv) there is no $\eta \in \Gamma \langle \beta \rangle$
 with $\Psi < \eta < (\Gamma ^{>})';$
with $\Psi < \eta < (\Gamma ^{>})';$
(v) $\Gamma ^{<}$
 is cofinal in $\Gamma \langle \beta \rangle ^{<},$
is cofinal in $\Gamma \langle \beta \rangle ^{<},$ and $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$
and $(\Gamma \langle \beta \rangle,\, \psi _{\beta })$ has asymptotic integration.
has asymptotic integration.
Proof. The first part of (i) follows from the recursion satisfied by $\beta _0,\,\ldots,\, \beta _n$![]() , the ${\boldsymbol {k}}$
, the ${\boldsymbol {k}}$![]() -linear independence of $\beta _0,\,\ldots,\, \beta _n$
-linear independence of $\beta _0,\,\ldots,\, \beta _n$![]() over $\Gamma$
over $\Gamma$![]() , and $\beta _n^{\dagger} \notin \Psi$
, and $\beta _n^{\dagger} \notin \Psi$![]() . Claim 1 in the proof of Proposition 4.1 gives (ii), which together with (i) yields (iii). Claim 2 in that proof gives (iv), which has (v) as an easy consequence.
. Claim 1 in the proof of Proposition 4.1 gives (ii), which together with (i) yields (iii). Claim 2 in that proof gives (iv), which has (v) as an easy consequence.
The next result is crucial in the proof of Theorem 0.1 in § 5. Here $(\Gamma ^*,\, \psi ^*)$![]() is equipped with an $H$
is equipped with an $H$![]() -cut $P^*$
-cut $P^*$![]() , and we set $P:= P^*\cap \Gamma = \Psi ^{\downarrow }$
, and we set $P:= P^*\cap \Gamma = \Psi ^{\downarrow }$![]() , and $P_{\gamma }:=P^*\cap \Gamma \langle \gamma \rangle$
, and $P_{\gamma }:=P^*\cap \Gamma \langle \gamma \rangle$![]() for $\gamma \in \Gamma ^*$
for $\gamma \in \Gamma ^*$![]() , so we have the $H$
, so we have the $H$![]() -triples $(\Gamma,\, \psi,\, P),\, (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma }) \subseteq (\Gamma ^*,\, \psi ^*,\, P^*)$
-triples $(\Gamma,\, \psi,\, P),\, (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma }) \subseteq (\Gamma ^*,\, \psi ^*,\, P^*)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() .
.
Lemma 4.5 Assume $(\Gamma ^*,\,\psi ^*)$![]() is closed, of Hahn type, and $\Gamma ^{<}$
is closed, of Hahn type, and $\Gamma ^{<}$![]() is not cofinal in $(\Gamma ^*)^{<}$
is not cofinal in $(\Gamma ^*)^{<}$![]() . Then for some $\delta \in (\Gamma ^*)^{>},$
. Then for some $\delta \in (\Gamma ^*)^{>},$![]() all $\gamma \in \Gamma ^*$
all $\gamma \in \Gamma ^*$![]() with $|\beta -\gamma | < \delta$
with $|\beta -\gamma | < \delta$![]() yield an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma })$
yield an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma })$![]() over $\Gamma$
over $\Gamma$![]() sending $\beta$
sending $\beta$![]() to $\gamma$
to $\gamma$![]() .
.
Proof. Suppose we are in Case (a) of Proposition 4.1. There are three subcases:
Subcase 1: $(\Gamma ^>)^{\dagger} < \eta < (\Gamma ^>)'$![]() and $\eta \in P^*$
and $\eta \in P^*$![]() for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$
for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$![]() . Fix such $\eta$
. Fix such $\eta$![]() and recall from Case 1 in the proof of Lemma 3.4 that $\Gamma$
and recall from Case 1 in the proof of Lemma 3.4 that $\Gamma$![]() is dense in $\Gamma +{\boldsymbol {k}}\eta =\Gamma +{\boldsymbol {k}}\beta$
is dense in $\Gamma +{\boldsymbol {k}}\eta =\Gamma +{\boldsymbol {k}}\beta$![]() . Thus, if $\varepsilon \in \Gamma ^*$
. Thus, if $\varepsilon \in \Gamma ^*$![]() and $0 < \varepsilon < \Gamma ^{>}$
and $0 < \varepsilon < \Gamma ^{>}$![]() , then $(\Gamma ^>)^{\dagger} < \eta -\varepsilon < \eta$
, then $(\Gamma ^>)^{\dagger} < \eta -\varepsilon < \eta$![]() . Moreover, $P^*$
. Moreover, $P^*$![]() has no largest element, so we can take $\varepsilon \in (\Gamma ^*)^{>}$
has no largest element, so we can take $\varepsilon \in (\Gamma ^*)^{>}$![]() so small that for all $\zeta \in \Gamma ^*$
so small that for all $\zeta \in \Gamma ^*$![]() with $|\eta -\zeta |<\varepsilon$
with $|\eta -\zeta |<\varepsilon$![]() we have $(\Gamma ^>)^{\dagger} < \zeta < (\Gamma ^>)'$
we have $(\Gamma ^>)^{\dagger} < \zeta < (\Gamma ^>)'$![]() and $\zeta \in P^*$
and $\zeta \in P^*$![]() ; in particular, such $\zeta$
; in particular, such $\zeta$![]() realizes the same cut in $\Gamma$
realizes the same cut in $\Gamma$![]() as $\eta$
as $\eta$![]() . Take $\alpha \in \Gamma$
. Take $\alpha \in \Gamma$![]() and $c\in {\boldsymbol {k}}^\times$
and $c\in {\boldsymbol {k}}^\times$![]() with $\beta =\alpha +c\eta$
with $\beta =\alpha +c\eta$![]() . Then for $\zeta$
. Then for $\zeta$![]() as above and $\gamma := \alpha +c\zeta$
as above and $\gamma := \alpha +c\zeta$![]() the condition $|\eta -\zeta |< \varepsilon$
the condition $|\eta -\zeta |< \varepsilon$![]() amounts to $|\beta -\gamma |< \delta :=|c|\varepsilon$
amounts to $|\beta -\gamma |< \delta :=|c|\varepsilon$![]() , with an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma })$
, with an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma })$![]() over $\Gamma$
over $\Gamma$![]() sending $\beta$
sending $\beta$![]() to $\gamma$
to $\gamma$![]() .
.
Subcase 2: $(\Gamma ^>)^{\dagger} < \eta < (\Gamma ^>)'$![]() and $\eta \notin P^*$
and $\eta \notin P^*$![]() for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$
for some $\eta \in \Gamma +{\boldsymbol {k}}\beta$![]() . This can be treated in the same way as Subcase 1.
. This can be treated in the same way as Subcase 1.
Subcase 3: there is no $\eta \in \Gamma +{\boldsymbol {k}}\beta$![]() with $(\Gamma ^>)^{\dagger} < \eta < (\Gamma ^>)'$
with $(\Gamma ^>)^{\dagger} < \eta < (\Gamma ^>)'$![]() . Take $\delta \in \Gamma ^*$
. Take $\delta \in \Gamma ^*$![]() such that $0 < \delta < \Gamma ^{>}$
such that $0 < \delta < \Gamma ^{>}$![]() . Then all $\gamma \in \Gamma ^*$
. Then all $\gamma \in \Gamma ^*$![]() with $|\gamma -\beta |< \delta$
with $|\gamma -\beta |< \delta$![]() realize the same cut in $\Gamma$
realize the same cut in $\Gamma$![]() as $\beta$
as $\beta$![]() : otherwise we would have $\alpha \in \Gamma$
: otherwise we would have $\alpha \in \Gamma$![]() with $0<|\alpha -\beta |< \Gamma ^{>}$
with $0<|\alpha -\beta |< \Gamma ^{>}$![]() , so $(\Gamma ^>)^{\dagger} < (\alpha -\beta )^{\dagger} < (\Gamma ^>)'$
, so $(\Gamma ^>)^{\dagger} < (\alpha -\beta )^{\dagger} < (\Gamma ^>)'$![]() , a contradiction. Now $(\Gamma ^*,\, \psi ^*)$
, a contradiction. Now $(\Gamma ^*,\, \psi ^*)$![]() is of Hahn type, so $[\Gamma +{\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}$
is of Hahn type, so $[\Gamma +{\boldsymbol {k}}\beta ]_{{\boldsymbol {k}}}=[\Gamma ]_{{\boldsymbol {k}}}$![]() . As in Case 3 in the proof of Lemma 3.4 this yields for any such $\gamma$
. As in Case 3 in the proof of Lemma 3.4 this yields for any such $\gamma$![]() an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma })$
an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \gamma \rangle,\, \psi _{\gamma },\, P_{\gamma })$![]() over $\Gamma$
over $\Gamma$![]() sending $\beta$
sending $\beta$![]() to $\gamma$
to $\gamma$![]() .
.
Assume we are in Case (b) of Proposition 4.1, and let $(\alpha _i)$![]() and $(\beta _i)$
and $(\beta _i)$![]() be as in that case. Let $\varepsilon \in \Gamma ^*$
be as in that case. Let $\varepsilon \in \Gamma ^*$![]() be such that $[\varepsilon ]_{{\boldsymbol {k}}}< [\beta _0]_{{\boldsymbol {k}}}$
be such that $[\varepsilon ]_{{\boldsymbol {k}}}< [\beta _0]_{{\boldsymbol {k}}}$![]() . Then $\beta _0+\varepsilon = (\beta +\varepsilon )-\alpha _0$
. Then $\beta _0+\varepsilon = (\beta +\varepsilon )-\alpha _0$![]() , $[\beta _0+\varepsilon ]_{{\boldsymbol {k}}}=[\beta _0]_{{\boldsymbol {k}}}$
, $[\beta _0+\varepsilon ]_{{\boldsymbol {k}}}=[\beta _0]_{{\boldsymbol {k}}}$![]() , and thus $(\beta _0+\varepsilon )^{\dagger} =\beta _0^{\dagger}$
, and thus $(\beta _0+\varepsilon )^{\dagger} =\beta _0^{\dagger}$![]() . It follows that with $\beta +\varepsilon$
. It follows that with $\beta +\varepsilon$![]() instead of $\beta$
instead of $\beta$![]() we are also in case (b), with associated sequences $(\alpha _i)$
we are also in case (b), with associated sequences $(\alpha _i)$![]() and $(\beta _{i,\varepsilon })$
and $(\beta _{i,\varepsilon })$![]() , with $\beta _{0,\varepsilon }:=\beta _0+\varepsilon$
, with $\beta _{0,\varepsilon }:=\beta _0+\varepsilon$![]() and $\beta _{i,\varepsilon }:= \beta _i$
and $\beta _{i,\varepsilon }:= \beta _i$![]() for $i\geqslant 1$
for $i\geqslant 1$![]() . As noted in the proof of Lemma 4.2, the sequences $(\alpha _i)$
. As noted in the proof of Lemma 4.2, the sequences $(\alpha _i)$![]() , $(\beta _i)$
, $(\beta _i)$![]() conform to the construction in the proof of Proposition 4.1, and so the latter proof yields an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \beta +\varepsilon \rangle,\, \psi _{\beta +\varepsilon },\, P_{\beta +\varepsilon })$
conform to the construction in the proof of Proposition 4.1, and so the latter proof yields an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_{\beta }) \to (\Gamma \langle \beta +\varepsilon \rangle,\, \psi _{\beta +\varepsilon },\, P_{\beta +\varepsilon })$![]() over $\Gamma$
over $\Gamma$![]() that sends $\beta _i$
that sends $\beta _i$![]() to $\beta _{i,\varepsilon }$
to $\beta _{i,\varepsilon }$![]() for each $i$
for each $i$![]() , and thus $\beta$
, and thus $\beta$![]() to $\beta +\varepsilon$
to $\beta +\varepsilon$![]() .
.
Next, assume we are in Case (c)$_n$![]() of Proposition 4.1, and let $\alpha _0,\,\ldots,\, \alpha _n,\,\beta _0,\,\ldots,\, \beta _n$
of Proposition 4.1, and let $\alpha _0,\,\ldots,\, \alpha _n,\,\beta _0,\,\ldots,\, \beta _n$![]() be as in that case. As before, let $\varepsilon \in \Gamma ^*$
be as in that case. As before, let $\varepsilon \in \Gamma ^*$![]() be such that $[\varepsilon ]_{{\boldsymbol {k}}}< [\beta _0]_{{\boldsymbol {k}}}$
be such that $[\varepsilon ]_{{\boldsymbol {k}}}< [\beta _0]_{{\boldsymbol {k}}}$![]() . Then $\beta _0+\varepsilon = (\beta +\varepsilon )-\alpha _0$
. Then $\beta _0+\varepsilon = (\beta +\varepsilon )-\alpha _0$![]() , $[\beta _0+\varepsilon ]_{{\boldsymbol {k}}}=[\beta _0]_{{\boldsymbol {k}}}$
, $[\beta _0+\varepsilon ]_{{\boldsymbol {k}}}=[\beta _0]_{{\boldsymbol {k}}}$![]() , so $(\beta _0+\varepsilon )^{\dagger} =\beta _0^{\dagger}$
, so $(\beta _0+\varepsilon )^{\dagger} =\beta _0^{\dagger}$![]() . Hence with $\beta +\varepsilon$
. Hence with $\beta +\varepsilon$![]() instead of $\beta$
instead of $\beta$![]() we are again in case (c)$_n$
we are again in case (c)$_n$![]() , with associated sequences $\alpha _0,\,\ldots,\, \alpha _n$
, with associated sequences $\alpha _0,\,\ldots,\, \alpha _n$![]() and $\beta _{0,\varepsilon },\, \ldots,\, \beta _{n,\varepsilon }$
and $\beta _{0,\varepsilon },\, \ldots,\, \beta _{n,\varepsilon }$![]() , with $\beta _{0,\varepsilon }:=\beta _0+\varepsilon$
, with $\beta _{0,\varepsilon }:=\beta _0+\varepsilon$![]() and $\beta _{i,\varepsilon }:= \beta _i$
and $\beta _{i,\varepsilon }:= \beta _i$![]() for $1\leqslant i\leqslant n$
for $1\leqslant i\leqslant n$![]() . Note also that $\beta$
. Note also that $\beta$![]() and $\beta +\varepsilon$
and $\beta +\varepsilon$![]() give rise to the same $\Delta =\Gamma + {\boldsymbol {k}}\beta _n^{\dagger} =\Gamma + {\boldsymbol {k}} \beta _{n,\varepsilon }^{\dagger}$
give rise to the same $\Delta =\Gamma + {\boldsymbol {k}}\beta _n^{\dagger} =\Gamma + {\boldsymbol {k}} \beta _{n,\varepsilon }^{\dagger}$![]() . It now follows from Lemma 4.3 that we have an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta }) \to (\Gamma \langle \beta +\varepsilon \rangle,\, \psi _{\beta +\varepsilon })$
. It now follows from Lemma 4.3 that we have an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta }) \to (\Gamma \langle \beta +\varepsilon \rangle,\, \psi _{\beta +\varepsilon })$![]() of $H$
of $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() that is the identity on $\Delta$
that is the identity on $\Delta$![]() and sends $\beta _i$
and sends $\beta _i$![]() to $\beta _{i,\varepsilon }$
to $\beta _{i,\varepsilon }$![]() for each $i\leqslant n$
for each $i\leqslant n$![]() , and thus, $\beta$
, and thus, $\beta$![]() to $\beta +\varepsilon$
to $\beta +\varepsilon$![]() . Since $\beta$
. Since $\beta$![]() and $\beta +\varepsilon$
and $\beta +\varepsilon$![]() yield the same $\Delta$
yield the same $\Delta$![]() , it follows easily from (vi), (vii), (viii) of Lemma 4.3 that this isomorphism maps $P_{\beta }$
, it follows easily from (vi), (vii), (viii) of Lemma 4.3 that this isomorphism maps $P_{\beta }$![]() onto $P_{\beta +\varepsilon }$
onto $P_{\beta +\varepsilon }$![]() .
.
Finally, assume we are in Case (d)$_n$![]() of Proposition 4.1, and let $\alpha _0,\,\ldots,\, \alpha _n,\,\beta _0,\,\ldots,\, \beta _n$
of Proposition 4.1, and let $\alpha _0,\,\ldots,\, \alpha _n,\,\beta _0,\,\ldots,\, \beta _n$![]() be as in that case. Let $\varepsilon \in \Gamma ^*$
be as in that case. Let $\varepsilon \in \Gamma ^*$![]() be such that $[\varepsilon ]_{{\boldsymbol {k}}}< [\beta _0]_{{\boldsymbol {k}}}$
be such that $[\varepsilon ]_{{\boldsymbol {k}}}< [\beta _0]_{{\boldsymbol {k}}}$![]() . Then $\beta _0+\varepsilon = {(\beta +\varepsilon )-\alpha _0}$
. Then $\beta _0+\varepsilon = {(\beta +\varepsilon )-\alpha _0}$![]() , $[\beta _0+\varepsilon ]_{{\boldsymbol {k}}}=[\beta _0]_{{\boldsymbol {k}}}$
, $[\beta _0+\varepsilon ]_{{\boldsymbol {k}}}=[\beta _0]_{{\boldsymbol {k}}}$![]() , so $(\beta _0+\varepsilon )^{\dagger} =\beta _0^{\dagger}$
, so $(\beta _0+\varepsilon )^{\dagger} =\beta _0^{\dagger}$![]() . Hence with $\beta +\varepsilon$
. Hence with $\beta +\varepsilon$![]() instead of $\beta$
instead of $\beta$![]() we are again in case (d)$_n$
we are again in case (d)$_n$![]() , with associated sequences $\alpha _0,\,\ldots,\, \alpha _n$
, with associated sequences $\alpha _0,\,\ldots,\, \alpha _n$![]() and $\beta _{0,\varepsilon },\, \ldots,\, \beta _{n,\varepsilon }$
and $\beta _{0,\varepsilon },\, \ldots,\, \beta _{n,\varepsilon }$![]() , with $\beta _{0,\varepsilon }:=\beta _0+\varepsilon$
, with $\beta _{0,\varepsilon }:=\beta _0+\varepsilon$![]() and $\beta _{i,\varepsilon }:= \beta _i$
and $\beta _{i,\varepsilon }:= \beta _i$![]() for $1\leqslant i\leqslant n$
for $1\leqslant i\leqslant n$![]() . Then Lemma 4.4 yields an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_\beta ) \to (\Gamma \langle \beta +\varepsilon \rangle, \psi _{\beta +\varepsilon },\, P_{\beta +\varepsilon })$
. Then Lemma 4.4 yields an isomorphism $(\Gamma \langle \beta \rangle,\, \psi _{\beta },\, P_\beta ) \to (\Gamma \langle \beta +\varepsilon \rangle, \psi _{\beta +\varepsilon },\, P_{\beta +\varepsilon })$![]() of $H$
of $H$![]() -triples over ${\boldsymbol {k}}$
-triples over ${\boldsymbol {k}}$![]() that is the identity on $\Gamma$
that is the identity on $\Gamma$![]() and sends $\beta _i$
and sends $\beta _i$![]() to $\beta _{i,\varepsilon }$
to $\beta _{i,\varepsilon }$![]() for each $i\leqslant n$
for each $i\leqslant n$![]() , and thus $\beta$
, and thus $\beta$![]() to $\beta +\varepsilon$
to $\beta +\varepsilon$![]() .
.
5. Closed $H$ -couples of Hahn type
-couples of Hahn type
So far we have treated $H$![]() -couples over ${\boldsymbol {k}}$
-couples over ${\boldsymbol {k}}$![]() as one-sorted structures, by keeping ${\boldsymbol {k}}$
as one-sorted structures, by keeping ${\boldsymbol {k}}$![]() fixed and having for each scalar $c$
fixed and having for each scalar $c$![]() a separate unary function symbol that is interpreted as scalar multiplication by $c$
a separate unary function symbol that is interpreted as scalar multiplication by $c$![]() . We now go to the setting where an $H$
. We now go to the setting where an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() is viewed as a $2$
is viewed as a $2$![]() -sorted structure with ${\boldsymbol {k}}$
-sorted structure with ${\boldsymbol {k}}$![]() as a second sort, and thus with “Hahn type” as a first-order condition. Extending an $H$
as a second sort, and thus with “Hahn type” as a first-order condition. Extending an $H$![]() -couple may now involve extending ${\boldsymbol {k}}$
-couple may now involve extending ${\boldsymbol {k}}$![]() , so we begin with a subsection on the process of scalar extension for Hahn spaces. We remind the reader that the ordered scalar field ${\boldsymbol {k}}$
, so we begin with a subsection on the process of scalar extension for Hahn spaces. We remind the reader that the ordered scalar field ${\boldsymbol {k}}$![]() is not necessarily real closed.
is not necessarily real closed.
Scalar extension
Let $\Gamma$![]() be a Hahn space over ${\boldsymbol {k}}$
be a Hahn space over ${\boldsymbol {k}}$![]() , and let ${\boldsymbol {k}}^*$
, and let ${\boldsymbol {k}}^*$![]() be an ordered field extension of ${\boldsymbol {k}}$
be an ordered field extension of ${\boldsymbol {k}}$![]() . Then we have the vector space $\Gamma _{{\boldsymbol {k}}^*}:= {\boldsymbol {k}}^*\otimes _{{\boldsymbol {k}}} \Gamma$
. Then we have the vector space $\Gamma _{{\boldsymbol {k}}^*}:= {\boldsymbol {k}}^*\otimes _{{\boldsymbol {k}}} \Gamma$![]() over ${\boldsymbol {k}}^*$
over ${\boldsymbol {k}}^*$![]() . We have the ${\boldsymbol {k}}$
. We have the ${\boldsymbol {k}}$![]() -linear embedding $\gamma \mapsto 1\otimes \gamma \colon \Gamma \to \Gamma _{{\boldsymbol {k}}^*}$
-linear embedding $\gamma \mapsto 1\otimes \gamma \colon \Gamma \to \Gamma _{{\boldsymbol {k}}^*}$![]() via which we identify $\Gamma$
via which we identify $\Gamma$![]() with a ${\boldsymbol {k}}$
with a ${\boldsymbol {k}}$![]() -linear subspace of $\Gamma _{{\boldsymbol {k}}^*}$
-linear subspace of $\Gamma _{{\boldsymbol {k}}^*}$![]() . We make $\Gamma _{{\boldsymbol {k}}^*}$
. We make $\Gamma _{{\boldsymbol {k}}^*}$![]() into a Hahn space over ${\boldsymbol {k}}^*$
into a Hahn space over ${\boldsymbol {k}}^*$![]() as follows: for any $\gamma \in \Gamma _{{\boldsymbol {k}}^*}^{\ne }$
as follows: for any $\gamma \in \Gamma _{{\boldsymbol {k}}^*}^{\ne }$![]() we have $\gamma =c_1\gamma _1+\cdots + c_m\gamma _m$
we have $\gamma =c_1\gamma _1+\cdots + c_m\gamma _m$![]() with $m\geqslant 1$
with $m\geqslant 1$![]() , $c_1,\,\ldots,\, c_m\in ({\boldsymbol {k}}^*)^\times$
, $c_1,\,\ldots,\, c_m\in ({\boldsymbol {k}}^*)^\times$![]() , $\gamma _1\ldots,\, \gamma _m\in \Gamma ^{>}$
, $\gamma _1\ldots,\, \gamma _m\in \Gamma ^{>}$![]() , $[\gamma _1]_{{\boldsymbol {k}}} > \cdots >[\gamma _m]_{{\boldsymbol {k}}}$
, $[\gamma _1]_{{\boldsymbol {k}}} > \cdots >[\gamma _m]_{{\boldsymbol {k}}}$![]() ; then $\gamma >0$
; then $\gamma >0$![]() iff $c_1>0$
iff $c_1>0$![]() . This makes $\Gamma$
. This makes $\Gamma$![]() into an ordered ${\boldsymbol {k}}$
into an ordered ${\boldsymbol {k}}$![]() -linear subspace of $\Gamma _{{\boldsymbol {k}}^*}$
-linear subspace of $\Gamma _{{\boldsymbol {k}}^*}$![]() , and we have an order-preserving bijection ${[\gamma ]_{{\boldsymbol {k}}}\to [\gamma ]_{{\boldsymbol {k}}^*}\colon [\Gamma ]_{{\boldsymbol {k}}} \to [\Gamma _{{\boldsymbol {k}}^*}]_{{\boldsymbol {k}}^*}}$
, and we have an order-preserving bijection ${[\gamma ]_{{\boldsymbol {k}}}\to [\gamma ]_{{\boldsymbol {k}}^*}\colon [\Gamma ]_{{\boldsymbol {k}}} \to [\Gamma _{{\boldsymbol {k}}^*}]_{{\boldsymbol {k}}^*}}$![]() .
.
Lemma 5.1 Assume $[\Gamma ^{\ne }]_{{\boldsymbol {k}}}$![]() has no least element. Then for every $\gamma ^{*}\in \Gamma _{{\boldsymbol {k}}^{*}}\setminus \Gamma$
has no least element. Then for every $\gamma ^{*}\in \Gamma _{{\boldsymbol {k}}^{*}}\setminus \Gamma$![]() there is an element $\varepsilon \in \Gamma ^{>}$
there is an element $\varepsilon \in \Gamma ^{>}$![]() such that $|\gamma ^{*}-\gamma |>\varepsilon$
such that $|\gamma ^{*}-\gamma |>\varepsilon$![]() for all $\gamma \in \Gamma$
for all $\gamma \in \Gamma$![]() .
.
Proof. Let $\gamma ^*\in \Gamma _{{\boldsymbol {k}}^*}\setminus \Gamma$![]() , so $\gamma ^*=c_1\gamma _1+\cdots + c_m\gamma _m$
, so $\gamma ^*=c_1\gamma _1+\cdots + c_m\gamma _m$![]() with $m\geqslant 1$
with $m\geqslant 1$![]() , $c_1,\,\ldots,\, c_m\in ({\boldsymbol {k}}^*)^\times$
, $c_1,\,\ldots,\, c_m\in ({\boldsymbol {k}}^*)^\times$![]() , $\gamma _1\ldots,\, \gamma _m\in \Gamma ^{>}$
, $\gamma _1\ldots,\, \gamma _m\in \Gamma ^{>}$![]() , $[\gamma _1]_{{\boldsymbol {k}}} > \cdots >[\gamma _m]_{{\boldsymbol {k}}}$
, $[\gamma _1]_{{\boldsymbol {k}}} > \cdots >[\gamma _m]_{{\boldsymbol {k}}}$![]() . To show that $\gamma ^*$
. To show that $\gamma ^*$![]() has the claimed property we can assume $c_1\notin {\boldsymbol {k}}$
has the claimed property we can assume $c_1\notin {\boldsymbol {k}}$![]() . Take any $\varepsilon \in \Gamma ^{>}$
. Take any $\varepsilon \in \Gamma ^{>}$![]() with $[\varepsilon ]_{{\boldsymbol {k}}} < [\gamma _1]_{{\boldsymbol {k}}}$
with $[\varepsilon ]_{{\boldsymbol {k}}} < [\gamma _1]_{{\boldsymbol {k}}}$![]() , and assume towards a contradiction that $\gamma \in \Gamma$
, and assume towards a contradiction that $\gamma \in \Gamma$![]() and $|\gamma ^*-\gamma |\leqslant \varepsilon$
and $|\gamma ^*-\gamma |\leqslant \varepsilon$![]() . Then $[\gamma ]_{{\boldsymbol {k}}^*}=[\gamma ^*]_{{\boldsymbol {k}}^*}=[\gamma _1]_{{\boldsymbol {k}}^*}$
. Then $[\gamma ]_{{\boldsymbol {k}}^*}=[\gamma ^*]_{{\boldsymbol {k}}^*}=[\gamma _1]_{{\boldsymbol {k}}^*}$![]() , so $[\gamma ]_{{\boldsymbol {k}}}=[\gamma _1]_{{\boldsymbol {k}}}$
, so $[\gamma ]_{{\boldsymbol {k}}}=[\gamma _1]_{{\boldsymbol {k}}}$![]() , and hence $[\gamma -c\gamma _1]_{{\boldsymbol {k}}}<[\gamma _1]_{{\boldsymbol {k}}}$
, and hence $[\gamma -c\gamma _1]_{{\boldsymbol {k}}}<[\gamma _1]_{{\boldsymbol {k}}}$![]() with $c\in {\boldsymbol {k}}$
with $c\in {\boldsymbol {k}}$![]() . In view of
. In view of
and $c_1\ne c$![]() , this yields a contradiction.
, this yields a contradiction.
We also have the following universal property:
Corollary 5.2 Any embedding $\Gamma \to \Gamma ^*$![]() of ordered vector spaces over ${\boldsymbol {k}}$
of ordered vector spaces over ${\boldsymbol {k}}$![]() into an ordered vector space $\Gamma ^*$
into an ordered vector space $\Gamma ^*$![]() over ${\boldsymbol {k}}^*$
over ${\boldsymbol {k}}^*$![]() such that the induced map $[\Gamma ]_{{\boldsymbol {k}}} \to [\Gamma ^*]_{{\boldsymbol {k}}^*}$
such that the induced map $[\Gamma ]_{{\boldsymbol {k}}} \to [\Gamma ^*]_{{\boldsymbol {k}}^*}$![]() is injective extends uniquely to an embedding $\Gamma _{{\boldsymbol {k}}^*} \to \Gamma ^*$
is injective extends uniquely to an embedding $\Gamma _{{\boldsymbol {k}}^*} \to \Gamma ^*$![]() of ordered vector spaces over ${\boldsymbol {k}}^*$
of ordered vector spaces over ${\boldsymbol {k}}^*$![]() .
.
Let $(\Gamma,\,\psi )$![]() be an $H$
be an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() of Hahn type and ${\boldsymbol {k}}^*$
of Hahn type and ${\boldsymbol {k}}^*$![]() an ordered field extension of ${\boldsymbol {k}}$
an ordered field extension of ${\boldsymbol {k}}$![]() . The $H$
. The $H$![]() -couple $(\Gamma,\, \psi )_{{\boldsymbol {k}}^*}:= (\Gamma _{{\boldsymbol {k}}^*},\, \psi _{{\boldsymbol {k}}^*})$
-couple $(\Gamma,\, \psi )_{{\boldsymbol {k}}^*}:= (\Gamma _{{\boldsymbol {k}}^*},\, \psi _{{\boldsymbol {k}}^*})$![]() over ${\boldsymbol {k}}^*$
over ${\boldsymbol {k}}^*$![]() is determined by requiring that $\psi _{{\boldsymbol {k}}^*}$
is determined by requiring that $\psi _{{\boldsymbol {k}}^*}$![]() extends $\psi$
extends $\psi$![]() . Note that then $(\Gamma,\, \psi )_{{\boldsymbol {k}}^*}$
. Note that then $(\Gamma,\, \psi )_{{\boldsymbol {k}}^*}$![]() is also of Hahn type and has the same $\Psi$
is also of Hahn type and has the same $\Psi$![]() -set as $(\Gamma,\,\psi )$
-set as $(\Gamma,\,\psi )$![]() . The following is close to [Reference Aschenbrenner and van den Dries1, Lemma 3.7], whose proof uses a form of Hahn's Embedding Theorem. Here we use instead Lemma 5.1.
. The following is close to [Reference Aschenbrenner and van den Dries1, Lemma 3.7], whose proof uses a form of Hahn's Embedding Theorem. Here we use instead Lemma 5.1.
Lemma 5.3 If $\gamma \in \Gamma$![]() is a gap in $(\Gamma,\,\psi ),$
is a gap in $(\Gamma,\,\psi ),$![]() then $\gamma$
then $\gamma$![]() remains a gap in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$
remains a gap in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$![]() . If $\gamma ^*$
. If $\gamma ^*$![]() is a gap in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$
is a gap in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$![]() , then $\gamma ^*\in \Gamma$
, then $\gamma ^*\in \Gamma$![]() . Thus, $(\Gamma,\, \psi )$
. Thus, $(\Gamma,\, \psi )$![]() has asymptotic integration if and only if $(\Gamma,\, \psi )_{{\boldsymbol {k}}^*}$
has asymptotic integration if and only if $(\Gamma,\, \psi )_{{\boldsymbol {k}}^*}$![]() has asymptotic integration.
has asymptotic integration.
Proof. Suppose towards a contradiction that $\gamma \in \Gamma$![]() is a gap in $(\Gamma,\,\psi )$
is a gap in $(\Gamma,\,\psi )$![]() , but not in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$
, but not in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$![]() . Then $\gamma =\alpha '$
. Then $\gamma =\alpha '$![]() with $\alpha \in \Gamma _{{\boldsymbol {k}}^*}^{>}\setminus \Gamma$
with $\alpha \in \Gamma _{{\boldsymbol {k}}^*}^{>}\setminus \Gamma$![]() . From $\gamma < (\Gamma ^{>})'$
. From $\gamma < (\Gamma ^{>})'$![]() we get $0<\alpha <\Gamma ^{>}$
we get $0<\alpha <\Gamma ^{>}$![]() , but this contradicts that by Lemma 5.1 we have $|\alpha |> \varepsilon$
, but this contradicts that by Lemma 5.1 we have $|\alpha |> \varepsilon$![]() for some $\varepsilon \in \Gamma ^{>}$
for some $\varepsilon \in \Gamma ^{>}$![]() .
.
Next, assume $\gamma ^*$![]() is a gap in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$
is a gap in $(\Gamma,\,\psi )_{{\boldsymbol {k}}^*}$![]() . Then $\Psi < \gamma ^* < (\Gamma ^{>})'$
. Then $\Psi < \gamma ^* < (\Gamma ^{>})'$![]() , and for all $\varepsilon \in \Gamma ^{>}$
, and for all $\varepsilon \in \Gamma ^{>}$![]() there are $\alpha \in \Psi$
there are $\alpha \in \Psi$![]() and $\beta \in (\Gamma ^{>})'$
and $\beta \in (\Gamma ^{>})'$![]() (namely $\alpha := \varepsilon ^{\dagger}$
(namely $\alpha := \varepsilon ^{\dagger}$![]() and $\beta := \varepsilon '$
and $\beta := \varepsilon '$![]() ) with $\beta -\alpha \leqslant \varepsilon$
) with $\beta -\alpha \leqslant \varepsilon$![]() . In view of Lemma 5.1 this yields $\gamma ^*\in \Gamma$
. In view of Lemma 5.1 this yields $\gamma ^*\in \Gamma$![]() .
.
Normalized $H$ -couples
-couples
Let $(\Gamma,\, \psi )$![]() be an $H$
be an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() . By [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.2], if $\Psi \cap \Gamma ^{>}\ne \emptyset$
. By [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.2], if $\Psi \cap \Gamma ^{>}\ne \emptyset$![]() , then $\psi (\gamma )=\gamma$
, then $\psi (\gamma )=\gamma$![]() for a unique $\gamma \in \Gamma ^{>}$
for a unique $\gamma \in \Gamma ^{>}$![]() ; this unique fixed point of $\psi$
; this unique fixed point of $\psi$![]() on $\Gamma ^{>}$
on $\Gamma ^{>}$![]() is then denoted by $1$
is then denoted by $1$![]() . Referring to $(\Gamma,\,\psi )$
. Referring to $(\Gamma,\,\psi )$![]() as a normalized $H$
as a normalized $H$![]() -couple means that ${\Psi \cap \Gamma ^{>}\ne \emptyset }$
-couple means that ${\Psi \cap \Gamma ^{>}\ne \emptyset }$![]() , and that we consider $\Gamma$
, and that we consider $\Gamma$![]() as equipped with this fixed point $1$
as equipped with this fixed point $1$![]() as a distinguished element. (The term “normalized” is justified, because for any $H$
as a distinguished element. (The term “normalized” is justified, because for any $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() with underlying ordered vector space $\Gamma \ne \{0\}$
with underlying ordered vector space $\Gamma \ne \{0\}$![]() we can arrange ${\Psi \cap \Gamma ^{>}\ne \emptyset }$
we can arrange ${\Psi \cap \Gamma ^{>}\ne \emptyset }$![]() by replacing its function $\psi$
by replacing its function $\psi$![]() with a suitable “shift” $\alpha +\psi$
with a suitable “shift” $\alpha +\psi$![]() where $\alpha \in \Gamma$
where $\alpha \in \Gamma$![]() .) For minor technical reasons, it is convenient to restrict our attention in the remainder of this paper to normalized $H$
.) For minor technical reasons, it is convenient to restrict our attention in the remainder of this paper to normalized $H$![]() -couples; this is hardly a loss of generality, as we saw. Note also that the $H$
-couples; this is hardly a loss of generality, as we saw. Note also that the $H$![]() -couple of $\mathbb {T}$
-couple of $\mathbb {T}$![]() is normalized by taking $1=v(x^{-1})$
is normalized by taking $1=v(x^{-1})$![]() .
.
Below we construe a normalized $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() as a $2$
as a $2$![]() -sorted structure
-sorted structure
where $(\Gamma,\,\psi )$![]() is an $H$
is an $H$![]() -couple as defined in the beginning of § 1, ${\boldsymbol {k}}$
-couple as defined in the beginning of § 1, ${\boldsymbol {k}}$![]() is an ordered field, and $\operatorname {sc}\colon {\boldsymbol {k}}\times \Gamma \to \Gamma$
is an ordered field, and $\operatorname {sc}\colon {\boldsymbol {k}}\times \Gamma \to \Gamma$![]() is a scalar multiplication that makes $\Gamma$
is a scalar multiplication that makes $\Gamma$![]() into an ordered vector space over ${\boldsymbol {k}}$
into an ordered vector space over ${\boldsymbol {k}}$![]() (but we shall write $c\gamma$
(but we shall write $c\gamma$![]() instead of $\operatorname {sc}(c,\,\gamma )$
instead of $\operatorname {sc}(c,\,\gamma )$![]() for $c\in {\boldsymbol {k}}$
for $c\in {\boldsymbol {k}}$![]() and $\gamma \in \Gamma$
and $\gamma \in \Gamma$![]() ), such that $\psi (c\gamma )=\psi (\gamma )$
), such that $\psi (c\gamma )=\psi (\gamma )$![]() for $c\in {\boldsymbol {k}}^\times$
for $c\in {\boldsymbol {k}}^\times$![]() , $\gamma \in \Gamma$
, $\gamma \in \Gamma$![]() ; in addition we assume $\Gamma$
; in addition we assume $\Gamma$![]() to be equipped with an element $1>0$
to be equipped with an element $1>0$![]() such that $\psi (1)=1$
such that $\psi (1)=1$![]() . Such $\boldsymbol {\Gamma }$
. Such $\boldsymbol {\Gamma }$![]() is said to be of Hahn type if the $H$
is said to be of Hahn type if the $H$![]() -couple $(\Gamma,\,\psi )$
-couple $(\Gamma,\,\psi )$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() is of Hahn type as defined in § 1. In the same way, we may consider a normalized $H$
is of Hahn type as defined in § 1. In the same way, we may consider a normalized $H$![]() -triple over ${\boldsymbol {k}}$
-triple over ${\boldsymbol {k}}$![]() as a $2$
as a $2$![]() -sorted structure
-sorted structure
The language and theory of normalized $H$ -triples of Hahn type
-triples of Hahn type
We construe a normalized $H$![]() -triple $\boldsymbol {\Gamma }=((\Gamma,\,\psi,\,P),\, {\boldsymbol {k}}; \operatorname {sc}\!)$
-triple $\boldsymbol {\Gamma }=((\Gamma,\,\psi,\,P),\, {\boldsymbol {k}}; \operatorname {sc}\!)$![]() of Hahn type as an $\mathcal {L}_H$
of Hahn type as an $\mathcal {L}_H$![]() -structure, where $\mathcal {L}_H$
-structure, where $\mathcal {L}_H$![]() is the two-sorted language with the following non-logical symbols:
is the two-sorted language with the following non-logical symbols:
(i) $P,\,<,\,0,\,1$
 ,$\infty,\,-,\, +,\,\psi$
,$\infty,\,-,\, +,\,\psi$ , interpreted as usual in $\Gamma _{\infty }:=\Gamma \cup \{\infty \}$
, interpreted as usual in $\Gamma _{\infty }:=\Gamma \cup \{\infty \}$ , the linear ordering on $\Gamma$
, the linear ordering on $\Gamma$ being extended to a linear order on $\Gamma _{\infty }$
being extended to a linear order on $\Gamma _{\infty }$ by $\gamma <\infty$
by $\gamma <\infty$ for $\gamma \in \Gamma$
for $\gamma \in \Gamma$ , and with $\infty$
, and with $\infty$ serving as a default value by setting $-\infty =\infty$
serving as a default value by setting $-\infty =\infty$ , $\gamma +\infty =\infty +\gamma =\infty +\infty =\psi (0)=\psi (\infty )=\infty$
, $\gamma +\infty =\infty +\gamma =\infty +\infty =\psi (0)=\psi (\infty )=\infty$ for $\gamma \in \Gamma$
for $\gamma \in \Gamma$ ;
;(ii) $<,\, 0,\, 1$
 , $\infty,\, -,\,+,\,\cdot$
, $\infty,\, -,\,+,\,\cdot$ , interpreted as usual in ${\boldsymbol {k}}_{\infty }:={\boldsymbol {k}}\cup \{\infty \}$
, interpreted as usual in ${\boldsymbol {k}}_{\infty }:={\boldsymbol {k}}\cup \{\infty \}$ , the linear ordering on ${\boldsymbol {k}}$
, the linear ordering on ${\boldsymbol {k}}$ being extended to a linear order on ${\boldsymbol {k}}_{\infty }$
being extended to a linear order on ${\boldsymbol {k}}_{\infty }$ by $c<\infty$
by $c<\infty$ for $c\in {\boldsymbol {k}}$
for $c\in {\boldsymbol {k}}$ , and with $\infty$
, and with $\infty$ serving as a default value by setting $-\infty =\infty$
serving as a default value by setting $-\infty =\infty$ , $c+\infty =\infty +c=\infty +\infty =c\infty =\infty c= \infty \infty =\infty$
, $c+\infty =\infty +c=\infty +\infty =c\infty =\infty c= \infty \infty =\infty$ for $c\in {\boldsymbol {k}}$
for $c\in {\boldsymbol {k}}$ ;
;(iii) a symbol $\operatorname {sc}$
 for the map ${\boldsymbol {k}}_{\infty }\times \Gamma _{\infty } \to \Gamma _{\infty }$
for the map ${\boldsymbol {k}}_{\infty }\times \Gamma _{\infty } \to \Gamma _{\infty }$ that is the scalar multiplication on ${\boldsymbol {k}}\times \Gamma$
that is the scalar multiplication on ${\boldsymbol {k}}\times \Gamma$ , and taking the value $\infty$
, and taking the value $\infty$ at all other points of ${\boldsymbol {k}}_{\infty }\times \Gamma _{\infty }$
at all other points of ${\boldsymbol {k}}_{\infty }\times \Gamma _{\infty }$ ;
;(iv) a symbol $:$
 for the function $\Gamma _{\infty }^2\to {\boldsymbol {k}}_{\infty }$
for the function $\Gamma _{\infty }^2\to {\boldsymbol {k}}_{\infty }$ that assigns to every $(\alpha,\,\beta )\in \Gamma ^2$
that assigns to every $(\alpha,\,\beta )\in \Gamma ^2$ with $[\alpha ]_{{\boldsymbol {k}}}\leqslant [\beta ]_{{\boldsymbol {k}}}$
with $[\alpha ]_{{\boldsymbol {k}}}\leqslant [\beta ]_{{\boldsymbol {k}}}$ and $\beta \ne 0$
and $\beta \ne 0$ the unique scalar $\alpha :\beta =c\in {\boldsymbol {k}}$
the unique scalar $\alpha :\beta =c\in {\boldsymbol {k}}$ such that $[{\alpha -c\beta }]_{{\boldsymbol {k}}}<[\beta ]_{{\boldsymbol {k}}}$
such that $[{\alpha -c\beta }]_{{\boldsymbol {k}}}<[\beta ]_{{\boldsymbol {k}}}$ , and assigns to all other pairs in $\Gamma _{\infty }^2$
, and assigns to all other pairs in $\Gamma _{\infty }^2$ the value $\infty$
the value $\infty$ .
.
The symbols in (i) should be distinguished from those in (ii) even though we use the same written signs for convenience. The two default values $\infty$![]() are included to make all primitives totally defined. Note that in (iv) we have $\alpha :\beta =0$
are included to make all primitives totally defined. Note that in (iv) we have $\alpha :\beta =0$![]() if $[\alpha ]_{{\boldsymbol {k}}} < [\beta ]_{{\boldsymbol {k}}}$
if $[\alpha ]_{{\boldsymbol {k}}} < [\beta ]_{{\boldsymbol {k}}}$![]() .
.
Using $a1:b1=a/b$![]() for $a,\,b\in {\boldsymbol {k}}$
for $a,\,b\in {\boldsymbol {k}}$![]() with $b\ne 0$
with $b\ne 0$![]() , we see that a substructure of a normalized $H$
, we see that a substructure of a normalized $H$![]() -triple of Hahn type is also a normalized $H$
-triple of Hahn type is also a normalized $H$![]() -triple of Hahn type, with possibly smaller scalar field. Thus, the $\mathcal {L}_H$
-triple of Hahn type, with possibly smaller scalar field. Thus, the $\mathcal {L}_H$![]() -theory of normalized $H$
-theory of normalized $H$![]() -triples of Hahn type has a universal axiomatization (which would be easy to specify). Let there be given normalized $H$
-triples of Hahn type has a universal axiomatization (which would be easy to specify). Let there be given normalized $H$![]() -triples of Hahn type,
-triples of Hahn type,
An embedding $\boldsymbol {\Gamma }_0 \to \boldsymbol {\Gamma }$![]() is a pair $i=(i_{\operatorname {v}},\, i_{\operatorname {s}})$
is a pair $i=(i_{\operatorname {v}},\, i_{\operatorname {s}})$![]() whose vector part $i_{\operatorname {v}}\colon \Gamma _0\to \Gamma$
whose vector part $i_{\operatorname {v}}\colon \Gamma _0\to \Gamma$![]() is an embedding of ordered abelian group and whose scalar part $i_{\operatorname {s}}\colon {\boldsymbol {k}}_0 \to {\boldsymbol {k}}$
is an embedding of ordered abelian group and whose scalar part $i_{\operatorname {s}}\colon {\boldsymbol {k}}_0 \to {\boldsymbol {k}}$![]() is an embedding of ordered fields such that $i_{\operatorname {v}}(c\gamma )=i_{\operatorname {s}}(c)i_{\operatorname {v}}(\gamma )$
is an embedding of ordered fields such that $i_{\operatorname {v}}(c\gamma )=i_{\operatorname {s}}(c)i_{\operatorname {v}}(\gamma )$![]() and $\gamma \in P_0\Leftrightarrow i_{\operatorname {v}}(\gamma )\in P$
and $\gamma \in P_0\Leftrightarrow i_{\operatorname {v}}(\gamma )\in P$![]() for all $c\in {\boldsymbol {k}}_0$
for all $c\in {\boldsymbol {k}}_0$![]() and $\gamma \in \Gamma _0$
and $\gamma \in \Gamma _0$![]() , and $i_{\operatorname {v}}(\psi _0(\gamma ))=\psi (i_{\operatorname {v}}(\gamma ))$
, and $i_{\operatorname {v}}(\psi _0(\gamma ))=\psi (i_{\operatorname {v}}(\gamma ))$![]() for all non-zero $\gamma \in \Gamma _0$
for all non-zero $\gamma \in \Gamma _0$![]() (and so $i_{\operatorname {v}}(1)=1$
(and so $i_{\operatorname {v}}(1)=1$![]() and $i_c(\alpha :\beta )=i_{\operatorname {v}}(\alpha ):i_{\operatorname {v}}(\beta )$
and $i_c(\alpha :\beta )=i_{\operatorname {v}}(\alpha ):i_{\operatorname {v}}(\beta )$![]() for all $\alpha,\,\beta \in \Gamma$
for all $\alpha,\,\beta \in \Gamma$![]() ). If ${\boldsymbol {k}}_0={\boldsymbol {k}}$
). If ${\boldsymbol {k}}_0={\boldsymbol {k}}$![]() , then an embedding $e\colon (\Gamma _0,\, \psi _0,\, P_0) \to (\Gamma,\,\psi,\,P)$
, then an embedding $e\colon (\Gamma _0,\, \psi _0,\, P_0) \to (\Gamma,\,\psi,\,P)$![]() of $H$
of $H$![]() -triples over ${\boldsymbol {k}}$
-triples over ${\boldsymbol {k}}$![]() in the usual sense yields an embedding $(e,\,\text {id}_{{\boldsymbol {k}}})\colon \boldsymbol {\Gamma }_0 \to \boldsymbol {\Gamma }$
in the usual sense yields an embedding $(e,\,\text {id}_{{\boldsymbol {k}}})\colon \boldsymbol {\Gamma }_0 \to \boldsymbol {\Gamma }$![]() as above.
as above.
Quantifier elimination
Let $T_H$![]() be the $\mathcal {L}_H$
be the $\mathcal {L}_H$![]() -theory of normalized closed $H$
-theory of normalized closed $H$![]() -triples of Hahn type, and recall that the $H$
-triples of Hahn type, and recall that the $H$![]() -couple of $\mathbb {T}$
-couple of $\mathbb {T}$![]() is naturally a model of $T_H$
is naturally a model of $T_H$![]() . In this subsection, we let $\boldsymbol {\Gamma } = ((\Gamma,\,\psi,\,P),\, {\boldsymbol {k}}; \operatorname {sc}\!)$
. In this subsection, we let $\boldsymbol {\Gamma } = ((\Gamma,\,\psi,\,P),\, {\boldsymbol {k}}; \operatorname {sc}\!)$![]() and $\boldsymbol {\Gamma }^* = ((\Gamma ^*,\,\psi ^*,\,P^*),\, {\boldsymbol {k}}^*; \operatorname {sc}^*\!)$
and $\boldsymbol {\Gamma }^* = ((\Gamma ^*,\,\psi ^*,\,P^*),\, {\boldsymbol {k}}^*; \operatorname {sc}^*\!)$![]() denote normalized closed $H$
denote normalized closed $H$![]() -triples of Hahn type, construed as models of $T_H$
-triples of Hahn type, construed as models of $T_H$![]() . The key embedding result is as follows:
. The key embedding result is as follows:
Proposition 5.4 Assume $\boldsymbol {\Gamma }^*$![]() is $\kappa$
is $\kappa$![]() -saturated for $\kappa =|\Gamma |^+$
-saturated for $\kappa =|\Gamma |^+$![]() . Let $\boldsymbol {\Gamma }_0$
. Let $\boldsymbol {\Gamma }_0$![]() be a substructure of $\boldsymbol {\Gamma }$
be a substructure of $\boldsymbol {\Gamma }$![]() with scalar field ${\boldsymbol {k}}_0$
with scalar field ${\boldsymbol {k}}_0$![]() . Let an embedding $i_0\colon \boldsymbol {\Gamma }_0\to \boldsymbol {\Gamma }^*$
. Let an embedding $i_0\colon \boldsymbol {\Gamma }_0\to \boldsymbol {\Gamma }^*$![]() be given, and an embedding $e\colon {\boldsymbol {k}} \to {\boldsymbol {k}}^*$
be given, and an embedding $e\colon {\boldsymbol {k}} \to {\boldsymbol {k}}^*$![]() of ordered fields such that $e|_{{\boldsymbol {k}}_0}=(i_0)_{\operatorname {s}}$
of ordered fields such that $e|_{{\boldsymbol {k}}_0}=(i_0)_{\operatorname {s}}$![]() . Then $i_0$
. Then $i_0$![]() can be extended to an embedding $i\colon \boldsymbol {\Gamma }\to \boldsymbol {\Gamma }^*$
can be extended to an embedding $i\colon \boldsymbol {\Gamma }\to \boldsymbol {\Gamma }^*$![]() such that $i_{\operatorname {s}}=e$
such that $i_{\operatorname {s}}=e$![]() .
.
Proof. By Corollary 5.2 on extending scalars, the remarks following it, and (to handle the $P$![]() -predicate) Lemma 5.3 we can reduce to the case ${\boldsymbol {k}}_0={\boldsymbol {k}}$
-predicate) Lemma 5.3 we can reduce to the case ${\boldsymbol {k}}_0={\boldsymbol {k}}$![]() . It remains to appeal to the embedding result established in the proof of Theorem 3.3.
. It remains to appeal to the embedding result established in the proof of Theorem 3.3.
In what follows, formula means $\mathcal {L}_H$![]() -formula. Let $x=(x_1,\,\ldots,\, x_m)$
-formula. Let $x=(x_1,\,\ldots,\, x_m)$![]() denote a tuple of distinct scalar variables and $y=(y_1,\,\ldots,\,y_n)$
denote a tuple of distinct scalar variables and $y=(y_1,\,\ldots,\,y_n)$![]() a tuple of distinct vector variables.
a tuple of distinct vector variables.
Corollary 5.5 Suppose that $\boldsymbol {\Gamma }$![]() is a substructure of $\boldsymbol {\Gamma }^*$
is a substructure of $\boldsymbol {\Gamma }^*$![]() . Then
. Then
Proof. The direction $\Rightarrow$![]() being trivial, we assume ${\boldsymbol {k}}\preccurlyeq {\boldsymbol {k}}^*$
being trivial, we assume ${\boldsymbol {k}}\preccurlyeq {\boldsymbol {k}}^*$![]() and shall derive $\boldsymbol {\Gamma }\preccurlyeq \boldsymbol {\Gamma }^*$
and shall derive $\boldsymbol {\Gamma }\preccurlyeq \boldsymbol {\Gamma }^*$![]() . By induction on formulas $\phi (x,\,y)$
. By induction on formulas $\phi (x,\,y)$![]() (with $x$
(with $x$![]() and $y$
and $y$![]() as above) we show that for all $\boldsymbol {\Gamma }$
as above) we show that for all $\boldsymbol {\Gamma }$![]() and $\boldsymbol {\Gamma }^*$
and $\boldsymbol {\Gamma }^*$![]() as in the hypothesis of the lemma and all $c\in {\boldsymbol {k}}^m$
as in the hypothesis of the lemma and all $c\in {\boldsymbol {k}}^m$![]() and $\gamma \in \Gamma ^n$
and $\gamma \in \Gamma ^n$![]() ,
,
For the inductive step, let $\phi =\exists z \theta$![]() , where $\theta =\theta (x,\,y,\,z)$
, where $\theta =\theta (x,\,y,\,z)$![]() is a formula and $z$
is a formula and $z$![]() is a single variable of the scalar or vector sort. The direction $\Rightarrow$
is a single variable of the scalar or vector sort. The direction $\Rightarrow$![]() in (??) holds by the (implicit) inductive assumption. Assume $\boldsymbol {\Gamma }^*\models \phi (c,\,\gamma )$
in (??) holds by the (implicit) inductive assumption. Assume $\boldsymbol {\Gamma }^*\models \phi (c,\,\gamma )$![]() where $c\in {\boldsymbol {k}}^m$
where $c\in {\boldsymbol {k}}^m$![]() and $\gamma \in \Gamma ^n$
and $\gamma \in \Gamma ^n$![]() . Take a $\kappa$
. Take a $\kappa$![]() -saturated elementary extension $\boldsymbol {\Gamma }_1$
-saturated elementary extension $\boldsymbol {\Gamma }_1$![]() of $\boldsymbol {\Gamma }$
of $\boldsymbol {\Gamma }$![]() , where $\kappa =|\Gamma ^*|^+$
, where $\kappa =|\Gamma ^*|^+$![]() . Let ${\boldsymbol {k}}_1$
. Let ${\boldsymbol {k}}_1$![]() be the scalar field of $\Gamma _1$
be the scalar field of $\Gamma _1$![]() . Then we have an elementary embedding $e\colon {\boldsymbol {k}}^*\to {\boldsymbol {k}}_1$
. Then we have an elementary embedding $e\colon {\boldsymbol {k}}^*\to {\boldsymbol {k}}_1$![]() that is the identity on ${\boldsymbol {k}}$
that is the identity on ${\boldsymbol {k}}$![]() . Proposition 5.4 (with $\boldsymbol {\Gamma }$
. Proposition 5.4 (with $\boldsymbol {\Gamma }$![]() , $\boldsymbol {\Gamma }^*$
, $\boldsymbol {\Gamma }^*$![]() , $\boldsymbol {\Gamma }_1$
, $\boldsymbol {\Gamma }_1$![]() in the roles of $\boldsymbol {\Gamma }_0$
in the roles of $\boldsymbol {\Gamma }_0$![]() , $\boldsymbol {\Gamma }$
, $\boldsymbol {\Gamma }$![]() , $\boldsymbol {\Gamma }^*$
, $\boldsymbol {\Gamma }^*$![]() ) gives an embedding $i\colon \boldsymbol {\Gamma }^*\to \boldsymbol {\Gamma }_1$
) gives an embedding $i\colon \boldsymbol {\Gamma }^*\to \boldsymbol {\Gamma }_1$![]() where $i_{\operatorname {s}}=e$
where $i_{\operatorname {s}}=e$![]() and $i_{\operatorname {v}}$
and $i_{\operatorname {v}}$![]() is the identity on $\Gamma$
is the identity on $\Gamma$![]() . By the (tacit) inductive hypothesis on $\theta$
. By the (tacit) inductive hypothesis on $\theta$![]() we obtain $\boldsymbol {\Gamma }_1\models \phi (c,\,\gamma )$
we obtain $\boldsymbol {\Gamma }_1\models \phi (c,\,\gamma )$![]() , and thus $\boldsymbol {\Gamma }\models \phi (c,\,\gamma )$
, and thus $\boldsymbol {\Gamma }\models \phi (c,\,\gamma )$![]() .
.
With $x$![]() , $y$
, $y$![]() as above, call a formula $\eta (x,\,y)$
as above, call a formula $\eta (x,\,y)$![]() a scalar formula if it has the form $\zeta (s_1(x,\,y),\,\ldots,\, s_N(x,\,y))$
a scalar formula if it has the form $\zeta (s_1(x,\,y),\,\ldots,\, s_N(x,\,y))$![]() where $\zeta (z_1,\,\ldots,\, z_N)$
where $\zeta (z_1,\,\ldots,\, z_N)$![]() is a formula in the language of ordered rings (as specified in (ii) of the description of $\mathcal {L}_H$
is a formula in the language of ordered rings (as specified in (ii) of the description of $\mathcal {L}_H$![]() ), where $z_1,\,\ldots,\, z_N$
), where $z_1,\,\ldots,\, z_N$![]() are distinct scalar variables and $s_1(x,\,y),\,\ldots,\, s_N(x,\,y)$
are distinct scalar variables and $s_1(x,\,y),\,\ldots,\, s_N(x,\,y)$![]() are scalar-valued terms of $\mathcal {L}_H$
are scalar-valued terms of $\mathcal {L}_H$![]() .
.
Theorem 5.6 Every formula $\phi (x,\,y)$![]() is $T_H$
is $T_H$![]() -equivalent to a boolean combination of scalar formulas $\eta (x,\,y)$
-equivalent to a boolean combination of scalar formulas $\eta (x,\,y)$![]() and atomic formulas $\alpha (x,\,y)$
and atomic formulas $\alpha (x,\,y)$![]() .
.
As a consequence, extending $T_H$![]() by axioms that the scalar field is real closed gives outright QE, without requiring scalar formulas.
by axioms that the scalar field is real closed gives outright QE, without requiring scalar formulas.
Proof. Suppose $(c,\,\gamma )\in {\boldsymbol {k}}^m\times \Gamma ^n$![]() and $(c^*,\, \gamma ^*)\in ({\boldsymbol {k}}^*)^m\times (\Gamma ^*)^n$
and $(c^*,\, \gamma ^*)\in ({\boldsymbol {k}}^*)^m\times (\Gamma ^*)^n$![]() satisfy the same scalar formulas $\eta (x,\,y)$
satisfy the same scalar formulas $\eta (x,\,y)$![]() and atomic formulas $\alpha (x,\,y)$
and atomic formulas $\alpha (x,\,y)$![]() in $\boldsymbol {\Gamma }$
in $\boldsymbol {\Gamma }$![]() and $\boldsymbol {\Gamma }^*$
and $\boldsymbol {\Gamma }^*$![]() , respectively. It suffices to derive from this assumption that $(c,\,\gamma )$
, respectively. It suffices to derive from this assumption that $(c,\,\gamma )$![]() and $(c^*,\,\gamma ^*)$
and $(c^*,\,\gamma ^*)$![]() satisfy the same formulas in $\boldsymbol {\Gamma }$
satisfy the same formulas in $\boldsymbol {\Gamma }$![]() and $\boldsymbol {\Gamma }^*$
and $\boldsymbol {\Gamma }^*$![]() . We may assume that $\boldsymbol {\Gamma }^*$
. We may assume that $\boldsymbol {\Gamma }^*$![]() is $\kappa$
is $\kappa$![]() -saturated where $\kappa =|\Gamma |^+$
-saturated where $\kappa =|\Gamma |^+$![]() . Let $\boldsymbol {\Gamma }_0$
. Let $\boldsymbol {\Gamma }_0$![]() with scalar field ${\boldsymbol {k}}_0$
with scalar field ${\boldsymbol {k}}_0$![]() be the substructure of $\boldsymbol {\Gamma }$
be the substructure of $\boldsymbol {\Gamma }$![]() generated by $(c,\,\gamma )$
generated by $(c,\,\gamma )$![]() . Since $(c,\,\gamma )$
. Since $(c,\,\gamma )$![]() and $(c^*,\,\gamma ^*)$
and $(c^*,\,\gamma ^*)$![]() realize the same atomic formulas $\alpha (x,\,y)$
realize the same atomic formulas $\alpha (x,\,y)$![]() , we have an embedding $i_0\colon \boldsymbol {\Gamma }_0\to \boldsymbol {\Gamma }^*$
, we have an embedding $i_0\colon \boldsymbol {\Gamma }_0\to \boldsymbol {\Gamma }^*$![]() such that $i_0(c)=c^*$
such that $i_0(c)=c^*$![]() and $i_0(\gamma )=\gamma ^*$
and $i_0(\gamma )=\gamma ^*$![]() . They also realize the same scalar formulas $\eta (x,\,y)$
. They also realize the same scalar formulas $\eta (x,\,y)$![]() , so we have an elementary embedding $e\colon {\boldsymbol {k}}\to {\boldsymbol {k}}^*$
, so we have an elementary embedding $e\colon {\boldsymbol {k}}\to {\boldsymbol {k}}^*$![]() agreeing with $(i_0)_{\operatorname {s}}$
agreeing with $(i_0)_{\operatorname {s}}$![]() on ${\boldsymbol {k}}_0$
on ${\boldsymbol {k}}_0$![]() . Proposition 5.4 then yields an embedding $i\colon \boldsymbol {\Gamma }\to \boldsymbol {\Gamma }^*$
. Proposition 5.4 then yields an embedding $i\colon \boldsymbol {\Gamma }\to \boldsymbol {\Gamma }^*$![]() extending $i_0$
extending $i_0$![]() with $i_{\operatorname {s}}=e$
with $i_{\operatorname {s}}=e$![]() . Then $i$
. Then $i$![]() is an elementary embedding by Corollary 5.5, so $(c,\,\gamma )$
is an elementary embedding by Corollary 5.5, so $(c,\,\gamma )$![]() and $(c^*,\,\gamma ^*)$
and $(c^*,\,\gamma ^*)$![]() do indeed satisfy the same formulas in $\boldsymbol {\Gamma }$
do indeed satisfy the same formulas in $\boldsymbol {\Gamma }$![]() and $\boldsymbol {\Gamma }^*$
and $\boldsymbol {\Gamma }^*$![]() .
.
Discrete definable sets
We are finally ready to prove the theorem announced in the introduction. We state it here in its natural general setting:
Theorem 5.7 Let $\boldsymbol {\Gamma }=((\Gamma,\,\psi,\,P),\, {\boldsymbol {k}}; \operatorname {sc}\!)$![]() be a normalized closed $H$
be a normalized closed $H$![]() -triple of Hahn type and let $X\subseteq \Gamma$
-triple of Hahn type and let $X\subseteq \Gamma$![]() be definable in $\boldsymbol {\Gamma }$
be definable in $\boldsymbol {\Gamma }$![]() . Then the following are equivalent:
. Then the following are equivalent:
(i) $X$
 is contained in a finite-dimensional ${\boldsymbol {k}}$
is contained in a finite-dimensional ${\boldsymbol {k}}$ -linear subspace of $\Gamma ;$
-linear subspace of $\Gamma ;$
(ii) $X$
 is discrete;
is discrete;(iii) $X$
 has empty interior in $\Gamma$
has empty interior in $\Gamma$ .
.
Proof. The direction (i) $\Rightarrow$![]() (ii) holds by Lemma 1.2. The direction (ii) $\Rightarrow$
(ii) holds by Lemma 1.2. The direction (ii) $\Rightarrow$![]() (iii) is obvious. (These two implications do not need $X$
(iii) is obvious. (These two implications do not need $X$![]() to be definable.)
to be definable.)
As to (iii) $\Rightarrow$![]() (i), assume $X$
(i), assume $X$![]() has empty interior. Take a formula $\phi (y)$
has empty interior. Take a formula $\phi (y)$![]() over $\boldsymbol {\Gamma }$
over $\boldsymbol {\Gamma }$![]() in a single vector variable $y$
in a single vector variable $y$![]() that defines the set $X$
that defines the set $X$![]() in $\boldsymbol {\Gamma }$
in $\boldsymbol {\Gamma }$![]() . We use Theorem 5.6 to arrange that $\phi (y)$
. We use Theorem 5.6 to arrange that $\phi (y)$![]() is a boolean combination of scalar formulas over $\boldsymbol {\Gamma }$
is a boolean combination of scalar formulas over $\boldsymbol {\Gamma }$![]() and atomic formulas over $\boldsymbol {\Gamma }$
and atomic formulas over $\boldsymbol {\Gamma }$![]() . Take a $|\Gamma |^+$
. Take a $|\Gamma |^+$![]() -saturated elementary extension $\boldsymbol {\Gamma }^*=((\Gamma ^*,\, \psi ^*,\,P^*),\,{\boldsymbol {k}}^*;\operatorname {sc}^*\!)$
-saturated elementary extension $\boldsymbol {\Gamma }^*=((\Gamma ^*,\, \psi ^*,\,P^*),\,{\boldsymbol {k}}^*;\operatorname {sc}^*\!)$![]() of $\boldsymbol {\Gamma }$
of $\boldsymbol {\Gamma }$![]() , and let $X^*\subseteq \Gamma ^*$
, and let $X^*\subseteq \Gamma ^*$![]() be defined by $\phi (y)$
be defined by $\phi (y)$![]() in $\boldsymbol {\Gamma }^*$
in $\boldsymbol {\Gamma }^*$![]() . We identify $\Gamma _{{\boldsymbol {k}}^*}$
. We identify $\Gamma _{{\boldsymbol {k}}^*}$![]() with ${\boldsymbol {k}}^*\Gamma \subseteq \Gamma ^*$
with ${\boldsymbol {k}}^*\Gamma \subseteq \Gamma ^*$![]() in the usual way. We Claim that $X^*\subseteq \Gamma _{{\boldsymbol {k}}^*}$
in the usual way. We Claim that $X^*\subseteq \Gamma _{{\boldsymbol {k}}^*}$![]() . (This gives (i) by Lemma 1.3.) Consider the substructure $\boldsymbol {\Gamma }_{{\boldsymbol {k}}^*}=((\Gamma _{{\boldsymbol {k}}^*},\,\psi _{{\boldsymbol {k}}^*},\, P_{{\boldsymbol {k}}^*}),\,{\boldsymbol {k}}^*;\operatorname {sc}^*\!)$
. (This gives (i) by Lemma 1.3.) Consider the substructure $\boldsymbol {\Gamma }_{{\boldsymbol {k}}^*}=((\Gamma _{{\boldsymbol {k}}^*},\,\psi _{{\boldsymbol {k}}^*},\, P_{{\boldsymbol {k}}^*}),\,{\boldsymbol {k}}^*;\operatorname {sc}^*\!)$![]() of $\boldsymbol {\Gamma }^*$
of $\boldsymbol {\Gamma }^*$![]() ; it has asymptotic integration by Lemma 5.3. Let $X_{{\boldsymbol {k}}^*}\subseteq \Gamma _{{\boldsymbol {k}}^*}$
; it has asymptotic integration by Lemma 5.3. Let $X_{{\boldsymbol {k}}^*}\subseteq \Gamma _{{\boldsymbol {k}}^*}$![]() be defined in $\boldsymbol {\Gamma }_{{\boldsymbol {k}}^*}$
be defined in $\boldsymbol {\Gamma }_{{\boldsymbol {k}}^*}$![]() by $\phi (y)$
by $\phi (y)$![]() . Then $X_{{\boldsymbol {k}}^*}=X^*\cap \Gamma _{{\boldsymbol {k}}^*}$
. Then $X_{{\boldsymbol {k}}^*}=X^*\cap \Gamma _{{\boldsymbol {k}}^*}$![]() , so our claim amounts to $X^*=X_{{\boldsymbol {k}}^*}$
, so our claim amounts to $X^*=X_{{\boldsymbol {k}}^*}$![]() . Suppose towards a contradiction that $\gamma ^*\in X^*\setminus X_{{\boldsymbol {k}}^*}$
. Suppose towards a contradiction that $\gamma ^*\in X^*\setminus X_{{\boldsymbol {k}}^*}$![]() . In particular, $\gamma ^*\in \Gamma ^*\setminus \Gamma _{{\boldsymbol {k}}^*}$
. In particular, $\gamma ^*\in \Gamma ^*\setminus \Gamma _{{\boldsymbol {k}}^*}$![]() . Saturation yields an $\varepsilon \in \Gamma ^*$
. Saturation yields an $\varepsilon \in \Gamma ^*$![]() such that $0 < \varepsilon < c^*\gamma$
such that $0 < \varepsilon < c^*\gamma$![]() for all positive $c^*$
for all positive $c^*$![]() in ${\boldsymbol {k}}^*$
in ${\boldsymbol {k}}^*$![]() and all positive $\gamma \in \Gamma$
and all positive $\gamma \in \Gamma$![]() , so $0 < \varepsilon < \Gamma _{{\boldsymbol {k}}^*}^{>}$
, so $0 < \varepsilon < \Gamma _{{\boldsymbol {k}}^*}^{>}$![]() , and thus $\Gamma _{{\boldsymbol {k}}^*}^{>}$
, and thus $\Gamma _{{\boldsymbol {k}}^*}^{>}$![]() is not coinitial in $(\Gamma ^*)^{>}$
is not coinitial in $(\Gamma ^*)^{>}$![]() . Lemma 4.5 then yields a $\delta >0$
. Lemma 4.5 then yields a $\delta >0$![]() in $\Gamma ^*$
in $\Gamma ^*$![]() such that all $\gamma \in \Gamma ^*$
such that all $\gamma \in \Gamma ^*$![]() with $|\gamma -\gamma ^*|< \delta$
with $|\gamma -\gamma ^*|< \delta$![]() yield an isomorphism
yield an isomorphism
of $H$![]() -triples over ${\boldsymbol {k}}^*$
-triples over ${\boldsymbol {k}}^*$![]() sending $\gamma ^*$
sending $\gamma ^*$![]() to $\gamma$
to $\gamma$![]() . Hence $s(\gamma ^*)=s(\gamma )$
. Hence $s(\gamma ^*)=s(\gamma )$![]() for such $\gamma$
for such $\gamma$![]() and any scalar-valued $\mathcal {L}_H$
and any scalar-valued $\mathcal {L}_H$![]() -term $s(y)$
-term $s(y)$![]() over $\boldsymbol {\Gamma }$
over $\boldsymbol {\Gamma }$![]() , and so $\boldsymbol {\Gamma }^*\models \phi (\gamma )$
, and so $\boldsymbol {\Gamma }^*\models \phi (\gamma )$![]() for those $\gamma$
for those $\gamma$![]() . Thus, the interval $(\gamma ^*-\delta,\, \gamma ^*+\delta )$
. Thus, the interval $(\gamma ^*-\delta,\, \gamma ^*+\delta )$![]() in $\Gamma ^*$
in $\Gamma ^*$![]() lies entirely in $X^*$
lies entirely in $X^*$![]() , contradicting that $X^*$
, contradicting that $X^*$![]() is discrete in $\Gamma ^*$
is discrete in $\Gamma ^*$![]() .
.
6. Further results about closed $H$ -couples
-couples
We briefly return to the one-sorted setting of $H$![]() -couples (or $H$
-couples (or $H$![]() -triples) and give two easy applications of Theorem 3.3.
-triples) and give two easy applications of Theorem 3.3.
Definable closure
Let $\boldsymbol {\Gamma }^*=(\Gamma ^*,\, \psi ^*,\,P^*)$![]() be a closed $H$
be a closed $H$![]() -triple over ${\boldsymbol {k}}$
-triple over ${\boldsymbol {k}}$![]() . Then we have the notion of the definable closure of a set $\Gamma \subseteq \Gamma ^*$
. Then we have the notion of the definable closure of a set $\Gamma \subseteq \Gamma ^*$![]() in $\boldsymbol {\Gamma }^*$
in $\boldsymbol {\Gamma }^*$![]() , and thus of such a set $\Gamma$
, and thus of such a set $\Gamma$![]() being definably closed in $\boldsymbol {\Gamma }^*$
being definably closed in $\boldsymbol {\Gamma }^*$![]() . If $\Gamma \subseteq \Gamma ^*$
. If $\Gamma \subseteq \Gamma ^*$![]() is definably closed in $\boldsymbol {\Gamma }^*$
is definably closed in $\boldsymbol {\Gamma }^*$![]() , then $\Gamma$
, then $\Gamma$![]() is (the underlying set of) a subgroup of $\Gamma ^*$
is (the underlying set of) a subgroup of $\Gamma ^*$![]() with $\psi ^*(\Gamma ^{\ne })\subseteq \Gamma$
with $\psi ^*(\Gamma ^{\ne })\subseteq \Gamma$![]() , and thus we have an $H$
, and thus we have an $H$![]() -triple $(\Gamma,\, \psi,\, P)$
-triple $(\Gamma,\, \psi,\, P)$![]() over ${\boldsymbol {k}}$
over ${\boldsymbol {k}}$![]() with $(\Gamma,\, \psi,\, P)\subseteq \boldsymbol {\Gamma }^*$
with $(\Gamma,\, \psi,\, P)\subseteq \boldsymbol {\Gamma }^*$![]() .
.
Proposition 6.1 Let $(\Gamma,\, \psi,\, P)$![]() be an $H$
be an $H$![]() -triple over ${\boldsymbol {k}}$
-triple over ${\boldsymbol {k}}$![]() with $(\Gamma,\, \psi,\, P)\subseteq \boldsymbol {\Gamma }$
with $(\Gamma,\, \psi,\, P)\subseteq \boldsymbol {\Gamma }$![]() . Then:
. Then:
Proof. For $\Rightarrow$![]() , note that for every $\gamma \in \Gamma$
, note that for every $\gamma \in \Gamma$![]() there is a unique $\alpha \in (\Gamma ^*)^{\ne }$
there is a unique $\alpha \in (\Gamma ^*)^{\ne }$![]() with $\gamma =\alpha '$
with $\gamma =\alpha '$![]() .
.
For the converse, assume that $(\Gamma,\, \psi )$![]() has asymptotic integration (so $P=\Psi ^{\downarrow }$
has asymptotic integration (so $P=\Psi ^{\downarrow }$![]() ). Iterating the construction of Lemma 3.1, we obtain an increasing continuous chain
). Iterating the construction of Lemma 3.1, we obtain an increasing continuous chain
of $H$![]() -triples contained in $(\Gamma ^*,\, \psi ^*,\, P^*)$
-triples contained in $(\Gamma ^*,\, \psi ^*,\, P^*)$![]() as substructures, with $(\Gamma _0,\, \psi _0,\, P_0)=(\Gamma,\, \psi,\, P)$
as substructures, with $(\Gamma _0,\, \psi _0,\, P_0)=(\Gamma,\, \psi,\, P)$![]() , such that every $(\Gamma _\lambda,\,\psi _\lambda,\, P_\lambda )$
, such that every $(\Gamma _\lambda,\,\psi _\lambda,\, P_\lambda )$![]() has asymptotic integration with $P_{\lambda }$
has asymptotic integration with $P_{\lambda }$![]() being the downward closure of $\Psi _0$
being the downward closure of $\Psi _0$![]() in $\Gamma _{\lambda }$
in $\Gamma _{\lambda }$![]() , and such that the union
, and such that the union
is closed. The reference to Lemma 3.1 means that for $\lambda < \lambda +1<\nu$![]() we have $\Gamma _{\lambda +1}=\Gamma _{\lambda }\oplus {\boldsymbol {k}}\alpha _{\lambda }$
we have $\Gamma _{\lambda +1}=\Gamma _{\lambda }\oplus {\boldsymbol {k}}\alpha _{\lambda }$![]() with $\alpha _{\lambda }>0$
with $\alpha _{\lambda }>0$![]() and $\alpha _{\lambda }^{\dagger} \in P_{\lambda }\setminus \psi _{\lambda }(\Gamma _{\lambda }^{\ne })$
and $\alpha _{\lambda }^{\dagger} \in P_{\lambda }\setminus \psi _{\lambda }(\Gamma _{\lambda }^{\ne })$![]() . That the chain is continuous means that $(\Gamma _\mu,\,\psi _\lambda,\, P_\mu )=\bigcup _{\lambda <\mu }(\Gamma _\lambda,\,\psi _\lambda,\, P_\lambda )$
. That the chain is continuous means that $(\Gamma _\mu,\,\psi _\lambda,\, P_\mu )=\bigcup _{\lambda <\mu }(\Gamma _\lambda,\,\psi _\lambda,\, P_\lambda )$![]() for limit ordinals $\mu < \nu$
for limit ordinals $\mu < \nu$![]() . Any such $(\Gamma ^{\operatorname {c}},\, \psi ^{\operatorname {c}},\, P^{\operatorname {c}})$
. Any such $(\Gamma ^{\operatorname {c}},\, \psi ^{\operatorname {c}},\, P^{\operatorname {c}})$![]() is clearly, an $H$
is clearly, an $H$![]() -closure of $(\Gamma,\, \psi,\, P)$
-closure of $(\Gamma,\, \psi,\, P)$![]() , which explains the superscript $\operatorname {c}$
, which explains the superscript $\operatorname {c}$![]() . Since $(\Gamma ^{\operatorname {c}},\, \psi ^{\operatorname {c}},\, P^{\operatorname {c}})\preccurlyeq (\Gamma ^*,\,\psi ^*,\,P^*)$
. Since $(\Gamma ^{\operatorname {c}},\, \psi ^{\operatorname {c}},\, P^{\operatorname {c}})\preccurlyeq (\Gamma ^*,\,\psi ^*,\,P^*)$![]() , any element of $\Gamma ^*$
, any element of $\Gamma ^*$![]() that is definable in $\boldsymbol {\Gamma }^*$
that is definable in $\boldsymbol {\Gamma }^*$![]() over $\Gamma$
over $\Gamma$![]() must lie in $\Gamma ^{\operatorname {c}}$
must lie in $\Gamma ^{\operatorname {c}}$![]() . So let $\gamma ^{\operatorname {c}}\in \Gamma ^{\operatorname {c}}\setminus \Gamma$
. So let $\gamma ^{\operatorname {c}}\in \Gamma ^{\operatorname {c}}\setminus \Gamma$![]() ; to show that then $\gamma ^{\operatorname {c}}$
; to show that then $\gamma ^{\operatorname {c}}$![]() is not definable in $\boldsymbol {\Gamma }^*$
is not definable in $\boldsymbol {\Gamma }^*$![]() over $\Gamma$
over $\Gamma$![]() it suffices by Theorem 3.3 that $\gamma ^{\operatorname {c}}$
it suffices by Theorem 3.3 that $\gamma ^{\operatorname {c}}$![]() realizes in $\boldsymbol {\Gamma }^*$
realizes in $\boldsymbol {\Gamma }^*$![]() the same quantifier-free type over $\Gamma$
the same quantifier-free type over $\Gamma$![]() as some $\gamma \in \Gamma ^{\operatorname {c}}$
as some $\gamma \in \Gamma ^{\operatorname {c}}$![]() with $\gamma \ne \gamma ^{\operatorname {c}}$
with $\gamma \ne \gamma ^{\operatorname {c}}$![]() . Take $\lambda$
. Take $\lambda$![]() with $\lambda < \lambda +1<\nu$
with $\lambda < \lambda +1<\nu$![]() such that $\gamma ^{\operatorname {c}}\in \Gamma _{\lambda +1}\setminus \Gamma _{\lambda }$
such that $\gamma ^{\operatorname {c}}\in \Gamma _{\lambda +1}\setminus \Gamma _{\lambda }$![]() . Then
. Then
Take any $\alpha \ne \alpha _{\lambda }$![]() in $\Gamma _{\lambda +1}^{>}$
in $\Gamma _{\lambda +1}^{>}$![]() such that $[\alpha ]_{{\boldsymbol {k}}}=[\alpha _{\lambda }]_{{\boldsymbol {k}}}$
such that $[\alpha ]_{{\boldsymbol {k}}}=[\alpha _{\lambda }]_{{\boldsymbol {k}}}$![]() . Then $\gamma ^{\operatorname {c}}\ne \gamma :=\gamma _{\lambda }+d\alpha$
. Then $\gamma ^{\operatorname {c}}\ne \gamma :=\gamma _{\lambda }+d\alpha$![]() . Lemma 3.1 gives an automorphism $\sigma$
. Lemma 3.1 gives an automorphism $\sigma$![]() of $(\Gamma _{\lambda +1},\, \psi _{\lambda +1},\, P_{\lambda +1})$
of $(\Gamma _{\lambda +1},\, \psi _{\lambda +1},\, P_{\lambda +1})$![]() over $\Gamma _{\lambda }$
over $\Gamma _{\lambda }$![]() with $\sigma (\alpha )=\alpha _{\lambda }$
with $\sigma (\alpha )=\alpha _{\lambda }$![]() , so $\sigma (\gamma ^{\operatorname {c}})=\gamma$
, so $\sigma (\gamma ^{\operatorname {c}})=\gamma$![]() . Thus, $\gamma ^{\operatorname {c}}$
. Thus, $\gamma ^{\operatorname {c}}$![]() and $\gamma$
and $\gamma$![]() realize in $\boldsymbol {\Gamma }^*$
realize in $\boldsymbol {\Gamma }^*$![]() the same quantifier-free type over $\Gamma$
the same quantifier-free type over $\Gamma$![]() .
.
A closure property of closed $H$ -couples
-couples
We show here how [Reference Aschenbrenner and van den Dries1, Properties A and B] and its variant [Reference Aschenbrenner, van den Dries and van der Hoeven2, § 9.9] follow from our QE.
Let $(\Gamma,\, \psi )$![]() be an $H$
be an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() . We extend ${\psi \colon \Gamma ^{\ne }\to \Gamma }$
. We extend ${\psi \colon \Gamma ^{\ne }\to \Gamma }$![]() to a function $\psi \colon \Gamma _{\infty } \to \Gamma _{\infty }$
to a function $\psi \colon \Gamma _{\infty } \to \Gamma _{\infty }$![]() by $\psi (0)=\psi (\infty ):= \infty$
by $\psi (0)=\psi (\infty ):= \infty$![]() . For $\alpha _1,\,\ldots,\,\alpha _n\in \Gamma$
. For $\alpha _1,\,\ldots,\,\alpha _n\in \Gamma$![]() , $n\geqslant 1$
, $n\geqslant 1$![]() , we define $\psi _{\alpha _1,\ldots,\alpha _n}\colon \Gamma _{\infty }\to \Gamma _{\infty }$
, we define $\psi _{\alpha _1,\ldots,\alpha _n}\colon \Gamma _{\infty }\to \Gamma _{\infty }$![]() by recursion on $n$
by recursion on $n$![]() :
:
Let $D$![]() be a subset of an ordered abelian group $\Delta$
be a subset of an ordered abelian group $\Delta$![]() . Call $D$
. Call $D$![]() bounded if $D\subseteq [p,\,q]$
bounded if $D\subseteq [p,\,q]$![]() for some $p\leqslant q$
for some $p\leqslant q$![]() in $\Delta$
in $\Delta$![]() , and otherwise, call $D$
, and otherwise, call $D$![]() unbounded. (These notions and the next one are with respect to the ambient $\Delta$
unbounded. (These notions and the next one are with respect to the ambient $\Delta$![]() .) A (convex) component of $D$
.) A (convex) component of $D$![]() is by definition a non-empty convex subset $S$
is by definition a non-empty convex subset $S$![]() of $\Delta$
of $\Delta$![]() such that $S\subseteq D$
such that $S\subseteq D$![]() and $S$
and $S$![]() is maximal with these properties. The components of $D$
is maximal with these properties. The components of $D$![]() partition the set $D$
partition the set $D$![]() : for $d\in D$
: for $d\in D$![]() the unique component of $D$
the unique component of $D$![]() containing $d$
containing $d$![]() is
is
Let $n\geqslant 1$![]() , and let $\alpha$
, and let $\alpha$![]() be a sequence $\alpha _1,\,\ldots,\, \alpha _n$
be a sequence $\alpha _1,\,\ldots,\, \alpha _n$![]() from $\Gamma$
from $\Gamma$![]() . We set
. We set
Thus,

One checks easily by induction on $n$![]() that for distinct $\gamma,\, \gamma '\in D_{\alpha }$
that for distinct $\gamma,\, \gamma '\in D_{\alpha }$![]() ,
,
Let $n\geqslant 1$![]() , let $\alpha _1,\,\ldots,\, \alpha _n\in \Gamma$
, let $\alpha _1,\,\ldots,\, \alpha _n\in \Gamma$![]() , set $\alpha :=(\alpha _1,\,\ldots,\,\alpha _n)$
, set $\alpha :=(\alpha _1,\,\ldots,\,\alpha _n)$![]() , and let $c_1,\,\ldots,\, c_n\in {\boldsymbol {k}}$
, and let $c_1,\,\ldots,\, c_n\in {\boldsymbol {k}}$![]() .
.
The next lemma is [Reference Aschenbrenner, van den Dries and van der Hoeven2, Lemma 9.9.3], generalized from ${\boldsymbol {k}}=\mathbb {Q}$![]() to arbitrary ${\boldsymbol {k}}$
to arbitrary ${\boldsymbol {k}}$![]() , with the same (easy) proof.
, with the same (easy) proof.
Lemma 6.2 The function
is strictly increasing. Moreover, this function has the intermediate value property on every component of $D_{\alpha }$![]() .
.
Proposition 6.3 Suppose $(\Gamma,\, \psi )$![]() is closed, $(\Gamma ^*,\,\psi ^*)$
is closed, $(\Gamma ^*,\,\psi ^*)$![]() is an $H$
is an $H$![]() -couple over ${\boldsymbol {k}}$
-couple over ${\boldsymbol {k}}$![]() extending $(\Gamma,\,\psi ),$
extending $(\Gamma,\,\psi ),$![]() and $\gamma \in \Gamma ^*$
and $\gamma \in \Gamma ^*$![]() is such that
is such that

Then $\gamma \in \Gamma$![]() .
.
Proof. By extending $(\Gamma ^*,\, \psi ^*)$![]() we arrange it to be closed. Then by Theorem 3.3, $(\Gamma,\,\psi,\,\Psi )\preccurlyeq (\Gamma ^*,\, \psi ^*,\, \Psi ^*)$
we arrange it to be closed. Then by Theorem 3.3, $(\Gamma,\,\psi,\,\Psi )\preccurlyeq (\Gamma ^*,\, \psi ^*,\, \Psi ^*)$![]() , and so we have $\beta \in \Gamma$
, and so we have $\beta \in \Gamma$![]() such that $\psi _{\alpha _1,\ldots,\alpha _n}(\beta )\ne \infty$
such that $\psi _{\alpha _1,\ldots,\alpha _n}(\beta )\ne \infty$![]() and
and
It remains to note that then $\beta =\gamma$![]() by Lemma 6.2.
by Lemma 6.2.
7. Final remarks
In [Reference Aschenbrenner and van den Dries1], we adopted the $2$![]() -sorted setting and “Hahn type” at the outset and only observed in its last section that much went through in a one-sorted setting without Hahn type assumption and just rational scalars. Here we have reversed this order, since our proof of Theorem 0.1 required various facts, such as Lemmas 2.7 and 4.5, about “one-sorted” closed $H$
-sorted setting and “Hahn type” at the outset and only observed in its last section that much went through in a one-sorted setting without Hahn type assumption and just rational scalars. Here we have reversed this order, since our proof of Theorem 0.1 required various facts, such as Lemmas 2.7 and 4.5, about “one-sorted” closed $H$![]() -couples over an arbitrary ordered scalar field that are not readily available in [Reference Aschenbrenner and van den Dries1].
-couples over an arbitrary ordered scalar field that are not readily available in [Reference Aschenbrenner and van den Dries1].
There remain several parts in [Reference Aschenbrenner and van den Dries1] that we have not tried to cover or extend here. These concern the definable closure of an $H$![]() -couple in an ambient closed $H$
-couple in an ambient closed $H$![]() -couple, the uniqueness of $H$
-couple, the uniqueness of $H$![]() -closures, the well-orderedness of $\Psi$
-closures, the well-orderedness of $\Psi$![]() for finitely generated $H$
for finitely generated $H$![]() -couples, the weak o-minimality of closed $H$
-couples, the weak o-minimality of closed $H$![]() -couples, and the local o-minimality and o-minimality at infinity of models of $T_H$
-couples, and the local o-minimality and o-minimality at infinity of models of $T_H$![]() . We alert the reader that our terminology (and notation) concerning asymptotic couples have evolved since [Reference Aschenbrenner and van den Dries1], and are now in line with [Reference Aschenbrenner, van den Dries and van der Hoeven2], and so comparisons with the material here and in [Reference Aschenbrenner and van den Dries1] require careful attention to the exact meaning of words.
. We alert the reader that our terminology (and notation) concerning asymptotic couples have evolved since [Reference Aschenbrenner and van den Dries1], and are now in line with [Reference Aschenbrenner, van den Dries and van der Hoeven2], and so comparisons with the material here and in [Reference Aschenbrenner and van den Dries1] require careful attention to the exact meaning of words.
We do intend to treat some of these topics in a follow-up, since our revisit also uncovered errors in the alleged proofs of weak o-minimality and local o-minimality in [Reference Aschenbrenner and van den Dries1]. These can be corrected using the present paper, but this is not entirely a routine matter.
Competing interests
The authors declare none.