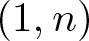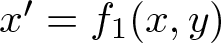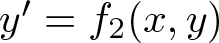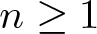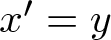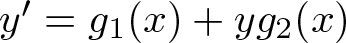1. Introduction and statement of the main results
Since the time of Liapunov, it has become evident that finding conditions that guarantee global asymptotic stability of an equilibrium point in a differential system, even in two dimensions, is a difficult problem. Liapunov’s approach is probably the most widespread general method used, though constructing a Liapunov function usually requires ingenuity, experience and some luck. For the two-dimensional autonomous system
with ![]() $f=(f_1,f_2) \colon \mathbb{R}^2 \to \mathbb{R}^2$, we seek for a set of easily verifiable conditions on the function f which can give global asymptotic stability. A result to this end was proven in 1993, the so-called Markus–Yamabe conjecture in two dimensions (see [Reference Fessler8, Reference Glutsyuk10, Reference Gutierrez11]). This result shows that the global asymptotic stability is obtained if the eigenvalues of the Jacobian matrix
$f=(f_1,f_2) \colon \mathbb{R}^2 \to \mathbb{R}^2$, we seek for a set of easily verifiable conditions on the function f which can give global asymptotic stability. A result to this end was proven in 1993, the so-called Markus–Yamabe conjecture in two dimensions (see [Reference Fessler8, Reference Glutsyuk10, Reference Gutierrez11]). This result shows that the global asymptotic stability is obtained if the eigenvalues of the Jacobian matrix ![]() $Df(x,y)$ have negative real part for all
$Df(x,y)$ have negative real part for all ![]() $(x,y) \in \mathbb{R}^2$. We remark that the Markus–Yamabe conjecture holds in the positive sense in
$(x,y) \in \mathbb{R}^2$. We remark that the Markus–Yamabe conjecture holds in the positive sense in ![]() $\mathbb{R}^2$ (see [Reference Fessler8, Reference Glutsyuk10, Reference Gutierrez11]), but it does not hold in
$\mathbb{R}^2$ (see [Reference Fessler8, Reference Glutsyuk10, Reference Gutierrez11]), but it does not hold in ![]() $\mathbb{R}^n$ with n > 2, see [Reference Bernat and Llibre1, Reference Cima, van den Essen, Gasull, Hubbers and Mañosas5].
$\mathbb{R}^n$ with n > 2, see [Reference Bernat and Llibre1, Reference Cima, van den Essen, Gasull, Hubbers and Mañosas5].
The aim of this paper is to weaken the Markus–Yamabe condition and still obtain global asymptotic stability for some classes of differential systems (1). The Markus–Yamabe condition ensures the global asymptotic stability, provided that the differential system has a unique equilibrium point, the trace of Df is negative (![]() $\mathrm{Tr} Df \lt 0$) and the determinant of Df is positive (
$\mathrm{Tr} Df \lt 0$) and the determinant of Df is positive (![]() $\det Df \gt 0$) for all
$\det Df \gt 0$) for all ![]() $(x,y) \in \mathbb{R}^2$. The trace condition guarantees that each region of finite area shrinks under the flow, while the determinant has a priori no known geometric interpretation. Several results (see [Reference Chamberland2, Reference Gasull, Llibre and Sotomayor9, Reference Olech12, Reference Sabatini13]) weaken the Markus–Yamabe condition by replacing the determinant condition by other conditions. These new requirements on the equilibrium point seem unremovable because they are necessary for the global asymptotic stability and they are easy to verify. Therefore, guided by the results in [Reference Chamberland, Llibre and Świrszcz4] for polynomial differential systems of degrees 2 and 7 in the plane (we recall that the degree of a polynomial map f is n if the components of f are polynomials of degree at most n), we consider the following open problem.
$(x,y) \in \mathbb{R}^2$. The trace condition guarantees that each region of finite area shrinks under the flow, while the determinant has a priori no known geometric interpretation. Several results (see [Reference Chamberland2, Reference Gasull, Llibre and Sotomayor9, Reference Olech12, Reference Sabatini13]) weaken the Markus–Yamabe condition by replacing the determinant condition by other conditions. These new requirements on the equilibrium point seem unremovable because they are necessary for the global asymptotic stability and they are easy to verify. Therefore, guided by the results in [Reference Chamberland, Llibre and Świrszcz4] for polynomial differential systems of degrees 2 and 7 in the plane (we recall that the degree of a polynomial map f is n if the components of f are polynomials of degree at most n), we consider the following open problem.
Open problem. Assume that ![]() $f \colon \mathbb{R}^2 \to \mathbb{R}^2$ is a polynomial map of degree n and satisfies the following conditions:
$f \colon \mathbb{R}^2 \to \mathbb{R}^2$ is a polynomial map of degree n and satisfies the following conditions:
(c1)
 $\mathrm{Tr}\ (D f) \lt 0$ for all
$\mathrm{Tr}\ (D f) \lt 0$ for all  $(x,y) \in \mathbb{R}^2$;
$(x,y) \in \mathbb{R}^2$;(c2) The differential equation (1) has a unique equilibrium point
 $p\in \mathbb{R}^2$.
$p\in \mathbb{R}^2$.(c3) The equilibrium point p is locally asymptotically stable.
Which is the largest family of planar differentiable systems (1) for which the assumptions (c1)–(c3) imply that p is globally asymptotically stable.
In view of [Reference Chamberland, Llibre and Świrszcz4], any planar differential system ![]() $(x,y)^{\prime}=f(x,y)$ with f being a polynomial map of degree two satisfying conditions (c1)–(c3) imply globally asymptotical stability. On the other hand, in view of [Reference Chamberland, Cima, Gasull and Mañosas3], there are polynomial differential systems
$(x,y)^{\prime}=f(x,y)$ with f being a polynomial map of degree two satisfying conditions (c1)–(c3) imply globally asymptotical stability. On the other hand, in view of [Reference Chamberland, Cima, Gasull and Mañosas3], there are polynomial differential systems ![]() $(x,y)^{\prime}=f(x,y)$ of degree seven (i.e. f has degree seven) for which conditions (c1)–(c3) do not imply globally asymptotical stability. In this paper, we will consider the polynomial differential systems
$(x,y)^{\prime}=f(x,y)$ of degree seven (i.e. f has degree seven) for which conditions (c1)–(c3) do not imply globally asymptotical stability. In this paper, we will consider the polynomial differential systems
 \begin{equation}
x^{\prime} = a_{1,0} x +a_{0,1} y, \qquad y^{\prime} = \sum_{j=1}^n b_{j,0} x^j + y \sum_{i=0}^m b_{i,1} x^i,
\end{equation}
\begin{equation}
x^{\prime} = a_{1,0} x +a_{0,1} y, \qquad y^{\prime} = \sum_{j=1}^n b_{j,0} x^j + y \sum_{i=0}^m b_{i,1} x^i,
\end{equation}with ![]() $m,n \ge 1$.
$m,n \ge 1$.
The following is our main result.
Theorem 1. Every planar polynomial differential system (2) satisfying conditions (c1)–(c3) is globally asymptotically stable.
As a corollary, we obtain the following result.
Corollary 2. Any generalized Liénard polynomial differential system
 \begin{equation*}
x^{\prime} =y, \qquad y^{\prime}= \sum_{j=1}^n b_{j,0} x^j + y \sum_{i=0}^m b_{i,1} x^i,
\end{equation*}
\begin{equation*}
x^{\prime} =y, \qquad y^{\prime}= \sum_{j=1}^n b_{j,0} x^j + y \sum_{i=0}^m b_{i,1} x^i,
\end{equation*}with ![]() $n,m$ integers satisfying conditions (c1)–(c3) is globally asymptotically stable.
$n,m$ integers satisfying conditions (c1)–(c3) is globally asymptotically stable.
Theorem 1 is proven in § 2. By taking ![]() $a_{1,0}$ and
$a_{1,0}$ and ![]() $a_{0,1} = 1$, Corollary 2 follows.
$a_{0,1} = 1$, Corollary 2 follows.
2. Proof of Theorem 1
The case n = 1 is trivial, and the case n = 2 was proved in [Reference Chamberland, Llibre and Świrszcz4]. So in this paper, we consider the case ![]() $n \ge 3$.
$n \ge 3$.
The proof of Theorem 1 is divided into different cases. We first need Theorem 3 (see below) that provides the local phase portraits of semi-hyperbolic equilibrium points for planar polynomial differential equations. See for instance [Reference Dumortier, Llibre and Artés7, Theorem 2.19] for a proof of Theorem 1.
Theorem 3. Let ![]() $(0,0)$ be an isolated equilibrium point of the planar polynomial differential system
$(0,0)$ be an isolated equilibrium point of the planar polynomial differential system
with F and G being polynomials without constant and linear terms in the variables x and y. Let ![]() $y=g(x)$ be the solution of
$y=g(x)$ be the solution of ![]() $y^{\prime}=y+G(x,y)=0$ and assume that
$y^{\prime}=y+G(x,y)=0$ and assume that ![]() $F(x,g(x))=a_m x^m + \cdots$, where
$F(x,g(x))=a_m x^m + \cdots$, where ![]() $m \ge 2$ and
$m \ge 2$ and ![]() $a_m \ne 0$. Then,
$a_m \ne 0$. Then,
(i) If m is odd and
 $a_m \gt 0$, then
$a_m \gt 0$, then  $(0,0)$ is an unstable node.
$(0,0)$ is an unstable node.(ii) If m is odd and
 $a_m \lt 0$, then
$a_m \lt 0$, then  $(0,0)$ is a saddle.
$(0,0)$ is a saddle.(iii) If m is even, then
 $(0,0)$ is a saddle node.
$(0,0)$ is a saddle node.
2.1. Case 1:  $a_{0,1}=0$
$a_{0,1}=0$
In this case, system (2) becomes
 \begin{equation}
x^{\prime} =a_{1,0} x=f_1(x,y), \qquad y^{\prime} = \sum_{j=1}^n b_{j,0} x^j + y \sum_{i=0}^m b_{i,1} x^i=f_2(x,y).
\end{equation}
\begin{equation}
x^{\prime} =a_{1,0} x=f_1(x,y), \qquad y^{\prime} = \sum_{j=1}^n b_{j,0} x^j + y \sum_{i=0}^m b_{i,1} x^i=f_2(x,y).
\end{equation}The divergence of this system is
 \begin{equation*}
\text{div} = \mathrm{Tr} Df =a_{1,0} + \sum_{i=0}^m b_{i,1} x^i.
\end{equation*}
\begin{equation*}
\text{div} = \mathrm{Tr} Df =a_{1,0} + \sum_{i=0}^m b_{i,1} x^i.
\end{equation*} Imposing the condition (c1), i.e., ![]() $\mathrm{Tr} Df \lt 0$ for all
$\mathrm{Tr} Df \lt 0$ for all ![]() $(x,y) \in \mathbb{R}^2$, we must have that m is even and
$(x,y) \in \mathbb{R}^2$, we must have that m is even and
 \begin{equation*}
a_{1,0} + b_{0,1} \lt 0, \qquad a_{1,0} + \sum_{i=0}^m b_{i,1} x^i =b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right), \quad b_{m,1} \lt 0,
\end{equation*}
\begin{equation*}
a_{1,0} + b_{0,1} \lt 0, \qquad a_{1,0} + \sum_{i=0}^m b_{i,1} x^i =b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right), \quad b_{m,1} \lt 0,
\end{equation*}with ![]() $\alpha_i, \beta_i \in \mathbb{R}$ and
$\alpha_i, \beta_i \in \mathbb{R}$ and ![]() $\beta_i \ne 0$. So, system (3) becomes
$\beta_i \ne 0$. So, system (3) becomes
 \begin{equation}
x^{\prime} =a_{1,0} x, \qquad \quad y^{\prime} = (b_{0,1}-a_{1,0}) y + \sum_{j=1}^n b_{j,0} x^j + y b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right).
\end{equation}
\begin{equation}
x^{\prime} =a_{1,0} x, \qquad \quad y^{\prime} = (b_{0,1}-a_{1,0}) y + \sum_{j=1}^n b_{j,0} x^j + y b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right).
\end{equation} Note that if  $b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2)=0$, then the line x = 0 is filled by equilibria and so this is not possible. So
$b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2)=0$, then the line x = 0 is filled by equilibria and so this is not possible. So  $b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2) \ne 0$ and
$b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2) \ne 0$ and ![]() $(0,0)$ is the unique equilibrium point of system (4) yielding that condition (c2) is satisfied.
$(0,0)$ is the unique equilibrium point of system (4) yielding that condition (c2) is satisfied.
On the other hand, the matrix ![]() $D f(0,0)$ has eigenvalues
$D f(0,0)$ has eigenvalues ![]() $a_{1,0}$ and
$a_{1,0}$ and  $ b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2)$. Imposing condition (c3) and taking into account that
$ b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2)$. Imposing condition (c3) and taking into account that  $b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2) \ne 0$, we must have
$b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2) \ne 0$, we must have ![]() $a_{1,0} \lt 0$ and
$a_{1,0} \lt 0$ and  $ b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2) \lt 0$, in which case the origin is a stable node.
$ b_{0,1}-a_{1,0}+b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2) \lt 0$, in which case the origin is a stable node.
Now, we shall prove that the origin is globally asymptotically stable. Any solution of Equation (4) with initial condition ![]() $(x_0,y_0)$ is given by
$(x_0,y_0)$ is given by ![]() $(x(y),y(t))$ with
$(x(y),y(t))$ with ![]() $x(t)=x_0 \,{\rm e}^{a_{1,0}t}$ and y(t) can be computed, thanks to the variation of constant method, that is, setting
$x(t)=x_0 \,{\rm e}^{a_{1,0}t}$ and y(t) can be computed, thanks to the variation of constant method, that is, setting
 \begin{equation*}
a(t)=b_{0,1}-a_{1,0} + b_{m,1} \prod_{i=1}^{m/2} \left((x_0\, {\rm e}^{a_{1,0}t}-\alpha_i)^2 + \beta_i^2\right),
\end{equation*}
\begin{equation*}
a(t)=b_{0,1}-a_{1,0} + b_{m,1} \prod_{i=1}^{m/2} \left((x_0\, {\rm e}^{a_{1,0}t}-\alpha_i)^2 + \beta_i^2\right),
\end{equation*}we get,
 \begin{equation*}
y(t)=
y_0\, {\rm e}^{\int_{t_0}^t a(s) \, {\rm d} s} + \sum_{i=0}^n b_{i,0} x_0^i \int_{t_0}^t {\rm e}^{a_{1,0}i \tau} {\rm e}^{\int_{\tau}^t a(s) \, {\rm d} s} \, {\rm d} \tau, \quad t \ge t_0.
\end{equation*}
\begin{equation*}
y(t)=
y_0\, {\rm e}^{\int_{t_0}^t a(s) \, {\rm d} s} + \sum_{i=0}^n b_{i,0} x_0^i \int_{t_0}^t {\rm e}^{a_{1,0}i \tau} {\rm e}^{\int_{\tau}^t a(s) \, {\rm d} s} \, {\rm d} \tau, \quad t \ge t_0.
\end{equation*} Since ![]() $a_{1,0} \lt 0$ and
$a_{1,0} \lt 0$ and ![]() $x_0 {\rm e}^{a_{1,0}t} \to 0$ when
$x_0 {\rm e}^{a_{1,0}t} \to 0$ when ![]() $t \to +\infty$, there exists T > 0 such that for
$t \to +\infty$, there exists T > 0 such that for ![]() $t \ge T$, we get
$t \ge T$, we get
 \begin{equation*}
a(t) \lt \frac12 \left(b_{0,1}-a_{1,0}+b_{m,1} \prod_{j=0}^{m/2} (\alpha_j^2 +\beta_j^2)\right) =:a^* \lt 0.
\end{equation*}
\begin{equation*}
a(t) \lt \frac12 \left(b_{0,1}-a_{1,0}+b_{m,1} \prod_{j=0}^{m/2} (\alpha_j^2 +\beta_j^2)\right) =:a^* \lt 0.
\end{equation*} Then, for ![]() $t,\tau \ge T$, we have
$t,\tau \ge T$, we have  $0 \le{\rm e}^{\int_\tau^t a(s) \, {\rm d}s } \le {\rm e}^{a^* (t-\tau)}$ and
$0 \le{\rm e}^{\int_\tau^t a(s) \, {\rm d}s } \le {\rm e}^{a^* (t-\tau)}$ and  ${\rm e}^{a_{1,0}i \tau} {\rm e}^{\int_{\tau}^t a(s) \, {\rm d} s} \le {\rm e}^{a_{1,0} i \tau + a^*(t-\tau)}$. Therefore, for
${\rm e}^{a_{1,0}i \tau} {\rm e}^{\int_{\tau}^t a(s) \, {\rm d} s} \le {\rm e}^{a_{1,0} i \tau + a^*(t-\tau)}$. Therefore, for ![]() $t ,t_0\ge T$ and
$t ,t_0\ge T$ and ![]() $t \ge t_0$,
$t \ge t_0$,
 \begin{equation*}
0 \le \lvert y(t) \rvert \le
\lvert y_0\rvert {\rm e}^{a^* (t-t_0)} +\sum_{i=0}^n \frac{\lvert b_{i,0} x_0^i\rvert}{\lvert a_{1,0}i -a^*\rvert} \left({\rm e}^{a_{1,0}it} -{\rm e}^{a_{1,0} i t_0 +a^*(t-t_0)}\right)
\end{equation*}
\begin{equation*}
0 \le \lvert y(t) \rvert \le
\lvert y_0\rvert {\rm e}^{a^* (t-t_0)} +\sum_{i=0}^n \frac{\lvert b_{i,0} x_0^i\rvert}{\lvert a_{1,0}i -a^*\rvert} \left({\rm e}^{a_{1,0}it} -{\rm e}^{a_{1,0} i t_0 +a^*(t-t_0)}\right)
\end{equation*}if ![]() $a^* \ne i a_{1,0}$ for any
$a^* \ne i a_{1,0}$ for any ![]() $i=0,1,\ldots,n$, and
$i=0,1,\ldots,n$, and
 \begin{align*}
0 \le& \lvert y(t) \rvert \le
\lvert y_0 \rvert {\rm e}^{a^* (t-t_0)} + \lvert b_{i^*,0} x_0^{i^*}\rvert (t-t_0) {\rm e}^{a^* t} \\ & \quad +\sum_{i=0, i \ne i*}^n \frac{\lvert b_{i,0} x_0^i\rvert}{\lvert a_{1,0} i -a^*\rvert} \left({\rm e}^{a_{1,0} i t} -{\rm e}^{a_{1,0} i t_0 +a^*(t-t_0)}\right)
\end{align*}
\begin{align*}
0 \le& \lvert y(t) \rvert \le
\lvert y_0 \rvert {\rm e}^{a^* (t-t_0)} + \lvert b_{i^*,0} x_0^{i^*}\rvert (t-t_0) {\rm e}^{a^* t} \\ & \quad +\sum_{i=0, i \ne i*}^n \frac{\lvert b_{i,0} x_0^i\rvert}{\lvert a_{1,0} i -a^*\rvert} \left({\rm e}^{a_{1,0} i t} -{\rm e}^{a_{1,0} i t_0 +a^*(t-t_0)}\right)
\end{align*}if there exists ![]() $i^* \in \{0,1,\ldots,n\}$ such that
$i^* \in \{0,1,\ldots,n\}$ such that ![]() $a^* = i^* a_{1,0}$.
$a^* = i^* a_{1,0}$.
In both cases using that ![]() $a_{1,0} \lt 0$ and
$a_{1,0} \lt 0$ and ![]() $a^* \lt 0$, we get that any solution
$a^* \lt 0$, we get that any solution ![]() $(x(t),y(t))$ with initial condition
$(x(t),y(t))$ with initial condition ![]() $(x_0,y_0)$ at time t 0 tends to the origin as
$(x_0,y_0)$ at time t 0 tends to the origin as ![]() $t \to +\infty$ and so the origin is globally asymptotically stable. The proof of the theorem is proved in this case.
$t \to +\infty$ and so the origin is globally asymptotically stable. The proof of the theorem is proved in this case.
2.2. Case 2:  $a_{0,1}\ne 0$
$a_{0,1}\ne 0$
In this case, introducing the change of variables:
Equation (2) writes
 \begin{equation*}
X^{\prime}=Y, \qquad Y^{\prime}=a_{1,0} Y+a_{0,1} \sum_{i=1}^n b_{i,0}X^i +(Y-a_{1,0}X)
\sum_{i=0}^m b_{i,1} X^i,
\end{equation*}
\begin{equation*}
X^{\prime}=Y, \qquad Y^{\prime}=a_{1,0} Y+a_{0,1} \sum_{i=1}^n b_{i,0}X^i +(Y-a_{1,0}X)
\sum_{i=0}^m b_{i,1} X^i,
\end{equation*}which also writes
 \begin{equation}
x^{\prime}=y, \qquad y^{\prime}= a_{1,0} y+ \sum_{i=1}^p \tilde b_{i,0}x^i + y
\sum_{i=0}^m b_{i,1} x^i,
\end{equation}
\begin{equation}
x^{\prime}=y, \qquad y^{\prime}= a_{1,0} y+ \sum_{i=1}^p \tilde b_{i,0}x^i + y
\sum_{i=0}^m b_{i,1} x^i,
\end{equation}where in order to avoid cumbersome notation, we have renamed the variables (X, Y) again as (x, y) and the new parameters  $\tilde b_{i,0}= a_{0,1} b_{i,0}- a_{1,0} b_{i-1,1}$ for
$\tilde b_{i,0}= a_{0,1} b_{i,0}- a_{1,0} b_{i-1,1}$ for ![]() $i=1,\ldots,p$, where
$i=1,\ldots,p$, where
 \begin{equation*}
p =\begin{cases}
n, & \text{if $n\ge m+1$ or $a_{1,0}=0$}, \\
m+1, & \text{if $n \le m+1$ and $a_{1,0} \ne 0$}.
\end{cases}
\end{equation*}
\begin{equation*}
p =\begin{cases}
n, & \text{if $n\ge m+1$ or $a_{1,0}=0$}, \\
m+1, & \text{if $n \le m+1$ and $a_{1,0} \ne 0$}.
\end{cases}
\end{equation*}Taking into account that
 \begin{equation*}
\mathrm{Tr} Df =a_{1,0}+
\sum_{i=0}^m b_{i,1} x^i
\end{equation*}
\begin{equation*}
\mathrm{Tr} Df =a_{1,0}+
\sum_{i=0}^m b_{i,1} x^i
\end{equation*}and imposing condition (c1), i.e. ![]() $\mathrm{Tr} Df \lt 0$ for all
$\mathrm{Tr} Df \lt 0$ for all ![]() $(x,y) \in \mathbb{R}^2$, we must have that m is even and
$(x,y) \in \mathbb{R}^2$, we must have that m is even and
 \begin{equation*}
a_{1,0}+ b_{0,1} \lt 0, \qquad a_{1,0} + \sum_{i=0}^m b_{i,1} x^i= b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right), \quad b_{m,1} \lt 0,
\end{equation*}
\begin{equation*}
a_{1,0}+ b_{0,1} \lt 0, \qquad a_{1,0} + \sum_{i=0}^m b_{i,1} x^i= b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right), \quad b_{m,1} \lt 0,
\end{equation*}with αi, ![]() $\beta_i \in \mathbb{R}$ and
$\beta_i \in \mathbb{R}$ and ![]() $\beta_i \ne 0$. Hence, system (5) becomes
$\beta_i \ne 0$. Hence, system (5) becomes
 \begin{equation}
\begin{split}
x^{\prime} & =y, \\
y^{\prime} & =\sum_{i=1}^p \tilde b_{i,0} x^i + y b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right) \\
& = A y + \sum_{i=1}^p \tilde b_{i,0} x^i + y\left( b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right),
\end{split}
\end{equation}
\begin{equation}
\begin{split}
x^{\prime} & =y, \\
y^{\prime} & =\sum_{i=1}^p \tilde b_{i,0} x^i + y b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right) \\
& = A y + \sum_{i=1}^p \tilde b_{i,0} x^i + y\left( b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right),
\end{split}
\end{equation}where  $A= b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2)$ and
$A= b_{m,1} \prod_{i=1}^{m/2} (\alpha_i^2 +\beta_i^2)$ and  $b_{m,1} \prod_{i=1}^{m/2} \big((x-\alpha_i)^2 + \beta_i^2\big)-A$ has no constant terms.
$b_{m,1} \prod_{i=1}^{m/2} \big((x-\alpha_i)^2 + \beta_i^2\big)-A$ has no constant terms.
Case 2.1: p even
Note that if ![]() $\tilde b_{10} \ne 0$, then Equation (6) has always an equilibrium point besides the origin, taking into account that
$\tilde b_{10} \ne 0$, then Equation (6) has always an equilibrium point besides the origin, taking into account that
 \begin{equation*}
y^{\prime}|_{y=0} = x\sum_{i=0}^{p-1} \tilde b_{i+1,0} x^i,
\end{equation*}
\begin{equation*}
y^{\prime}|_{y=0} = x\sum_{i=0}^{p-1} \tilde b_{i+1,0} x^i,
\end{equation*}with  $\tilde b_{1,0} \tilde b_{p,0}\ne 0$ and p − 1 being odd (equation
$\tilde b_{1,0} \tilde b_{p,0}\ne 0$ and p − 1 being odd (equation  $\sum_{i=0}^{p-1} \tilde b_{i+1,0} x^i=0$ has always a real solution different from x = 0). Therefore, in order that condition (c2) is fulfilled, we must have
$\sum_{i=0}^{p-1} \tilde b_{i+1,0} x^i=0$ has always a real solution different from x = 0). Therefore, in order that condition (c2) is fulfilled, we must have  $\tilde b_{1,0}=0$. In this case, system (6) becomes
$\tilde b_{1,0}=0$. In this case, system (6) becomes
 \begin{equation}
x^{\prime} =y, \qquad
y^{\prime} = A y + \sum_{i=2}^p \tilde b_{i,0} x^i + y\left( b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right).
\end{equation}
\begin{equation}
x^{\prime} =y, \qquad
y^{\prime} = A y + \sum_{i=2}^p \tilde b_{i,0} x^i + y\left( b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right).
\end{equation} In this case, the origin is semi-hyperbolic, and in order to apply Theorem 3, we must write Equation (7) in canonical Jordan form. For doing this, we apply the change of variables ![]() $X=x -Y/A$, Y = y, and system (7) becomes
$X=x -Y/A$, Y = y, and system (7) becomes
 \begin{equation*}
\begin{split}
X^{\prime} & = - \frac{1}{A} \left( \sum_{i=2}^p \tilde b_{i,0} \left(X + \frac{Y}{A}\right)^i+Y b_{m,1} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)\right)
, \\
Y^{\prime} & =A Y + \sum_{i=2}^p \tilde b_{i,0} \left(X + \frac{Y}{A}\right)^i+Y \left( b_{m,1} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)-A\right).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
X^{\prime} & = - \frac{1}{A} \left( \sum_{i=2}^p \tilde b_{i,0} \left(X + \frac{Y}{A}\right)^i+Y b_{m,1} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)\right)
, \\
Y^{\prime} & =A Y + \sum_{i=2}^p \tilde b_{i,0} \left(X + \frac{Y}{A}\right)^i+Y \left( b_{m,1} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)-A\right).
\end{split}
\end{equation*} Now, after rescaling by the time variable ![]() ${\rm d} s = A \, {\rm d}t$, and using Newton’s binomial formula, we obtain the system in canonical normal form:
${\rm d} s = A \, {\rm d}t$, and using Newton’s binomial formula, we obtain the system in canonical normal form:
 \begin{equation}
\begin{split}
X^{\prime} & = -\sum_{i=2}^p \frac {\tilde b_{i,0} }{A^2} \sum_{j=0}^i \binom{i}{j} \frac{X^j Y^{i-j}}{A^{i-j}}-Y \left(\frac{b_{m,1}}{A^2} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)-\frac 1 A \right)
, \\
Y^{\prime} & = Y + \sum_{i=2}^p \frac {\tilde b_{i,0} }{A} \sum_{j=0}^i \binom{i}{j} \frac{X^j Y^{i-j}}{A^{i-j}}+\frac{Y}A \left( b_{m,1} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)-A\right),
\end{split}
\end{equation}
\begin{equation}
\begin{split}
X^{\prime} & = -\sum_{i=2}^p \frac {\tilde b_{i,0} }{A^2} \sum_{j=0}^i \binom{i}{j} \frac{X^j Y^{i-j}}{A^{i-j}}-Y \left(\frac{b_{m,1}}{A^2} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)-\frac 1 A \right)
, \\
Y^{\prime} & = Y + \sum_{i=2}^p \frac {\tilde b_{i,0} }{A} \sum_{j=0}^i \binom{i}{j} \frac{X^j Y^{i-j}}{A^{i-j}}+\frac{Y}A \left( b_{m,1} \prod_{i=1}^{m/2} \left(\left(X + \frac{Y}{A}-\alpha_i\right)^2 + \beta_i^2\right)-A\right),
\end{split}
\end{equation}where now the prime means derivative in the new time s (note that since A < 0, the original system in time t changes the direction of the orbits). Applying Theorem 3, we get that
 \begin{equation*}
Y=- \tilde b_{2,0} X^2/A + \cdots \ \text{and then} \ F(X,Y)= - \tilde b_{2,0} X^2/A^2+\cdots,
\end{equation*}
\begin{equation*}
Y=- \tilde b_{2,0} X^2/A + \cdots \ \text{and then} \ F(X,Y)= - \tilde b_{2,0} X^2/A^2+\cdots,
\end{equation*}implying that the origin ![]() $(0,0)$ is a saddle-node, which is not possible. So in order that condition (c3) is fulfilled, we must have
$(0,0)$ is a saddle-node, which is not possible. So in order that condition (c3) is fulfilled, we must have  $\tilde b_{2,0}=0$, but then system (7) would be of the form
$\tilde b_{2,0}=0$, but then system (7) would be of the form
 \begin{equation*}
x^{\prime}=y, \qquad y^{\prime}=A y + x^3 \sum_{i=0}^{p-3} \tilde b_{i+3,0} x^{i} + y\left( b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right),
\end{equation*}
\begin{equation*}
x^{\prime}=y, \qquad y^{\prime}=A y + x^3 \sum_{i=0}^{p-3} \tilde b_{i+3,0} x^{i} + y\left( b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right),
\end{equation*}and the equation  $\sum_{i=0}^{p-3} \tilde b_{i+3,0} x^{i}=0$ has a real solution different from x = 0 unless
$\sum_{i=0}^{p-3} \tilde b_{i+3,0} x^{i}=0$ has a real solution different from x = 0 unless  $\tilde b_{3,0}=0$, but then again applying Theorem 3, we get that
$\tilde b_{3,0}=0$, but then again applying Theorem 3, we get that
 \begin{equation*}
Y=- \tilde b_{4,0} X^4/A + \cdots, \ \text{and then} \ F(X,Y)= - \tilde b_{4,0} X^4/A^2 +\cdots,
\end{equation*}
\begin{equation*}
Y=- \tilde b_{4,0} X^4/A + \cdots, \ \text{and then} \ F(X,Y)= - \tilde b_{4,0} X^4/A^2 +\cdots,
\end{equation*}implying that the origin ![]() $(0,0)$ is a saddle-node, which is not possible. Proceeding inductively, we conclude that
$(0,0)$ is a saddle-node, which is not possible. Proceeding inductively, we conclude that  $\tilde b_{i,0}=0$ for
$\tilde b_{i,0}=0$ for ![]() $i \ge 1$, and in this case, taking into account that p is even, we get that the origin is a saddle-node and condition (c3) is not satisfied. In short, in this case, no system satisfies conditions (c1)–(c3) and there is nothing to prove.
$i \ge 1$, and in this case, taking into account that p is even, we get that the origin is a saddle-node and condition (c3) is not satisfied. In short, in this case, no system satisfies conditions (c1)–(c3) and there is nothing to prove.
Case 2.2: p odd
Note that if ![]() $\tilde b_{10} \ne 0$, the matrix
$\tilde b_{10} \ne 0$, the matrix ![]() $D f(0,0)$ has eigenvalues:
$D f(0,0)$ has eigenvalues:
 \begin{equation*}
\lambda_{\pm} =\frac 1 2 \left(A\pm \sqrt{A^2 + 4 \tilde b_{1,0}}\right),
\end{equation*}
\begin{equation*}
\lambda_{\pm} =\frac 1 2 \left(A\pm \sqrt{A^2 + 4 \tilde b_{1,0}}\right),
\end{equation*}and imposing condition (c3), we must have  $\tilde b_{1,0} \lt 0$, and since A < 0, the origin is a stable node if
$\tilde b_{1,0} \lt 0$, and since A < 0, the origin is a stable node if  $A^2 + 4 \tilde b_{1,0}\ge 0$ and a stable focus if
$A^2 + 4 \tilde b_{1,0}\ge 0$ and a stable focus if  $A^2 + 4 \tilde b_{1,0} \lt 0$.
$A^2 + 4 \tilde b_{1,0} \lt 0$.
If  $\tilde b_{1,0}=0$, then we get system (7) and the origin is semi-hyperbolic. Proceeding as for Case 2.1, we get that if
$\tilde b_{1,0}=0$, then we get system (7) and the origin is semi-hyperbolic. Proceeding as for Case 2.1, we get that if  $\tilde b_{2,0} \ne 0$, then the origin is a saddle-node, which is not possible. So,
$\tilde b_{2,0} \ne 0$, then the origin is a saddle-node, which is not possible. So,  $\tilde b_{2,0}=0$. Now applying Theorem 3 to system (8), we get that
$\tilde b_{2,0}=0$. Now applying Theorem 3 to system (8), we get that  $Y=- \tilde b_{3,0} X^3/A + \cdots$ and then
$Y=- \tilde b_{3,0} X^3/A + \cdots$ and then  $F(X,Y)= - \tilde b_{3,0} X^3/A^2+\cdots $, implying that, if
$F(X,Y)= - \tilde b_{3,0} X^3/A^2+\cdots $, implying that, if  $\tilde b_{3,0} \ne 0$, for the origin to be a node, we must have
$\tilde b_{3,0} \ne 0$, for the origin to be a node, we must have  $\tilde b_{3,0} \lt 0$. If
$\tilde b_{3,0} \lt 0$. If  $\tilde b_{3,0}=0$, then in order that condition (c3) is fulfilled, we must have
$\tilde b_{3,0}=0$, then in order that condition (c3) is fulfilled, we must have  $\tilde b_{4,0}=0$ and so on. In short, in order that condition (c3) if fulfilled for system (7), there must exists an odd integer
$\tilde b_{4,0}=0$ and so on. In short, in order that condition (c3) if fulfilled for system (7), there must exists an odd integer ![]() $i^* \in \{1,\ldots,n\}$ for which
$i^* \in \{1,\ldots,n\}$ for which  $\tilde b_{i^*,0} \lt 0$ and system (7) writes
$\tilde b_{i^*,0} \lt 0$ and system (7) writes
 \begin{equation*}
x^{\prime} =y, \qquad y^{\prime} =A y + x^{i^*} \sum_{i=0}^{p-i^*} \tilde b_{i+i^*,0} x^{i} + y\left(b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right).
\end{equation*}
\begin{equation*}
x^{\prime} =y, \qquad y^{\prime} =A y + x^{i^*} \sum_{i=0}^{p-i^*} \tilde b_{i+i^*,0} x^{i} + y\left(b_{m,1} \prod_{i=1}^{m/2} \left((x-\alpha_i)^2 + \beta_i^2\right)-A \right).
\end{equation*} Note that ![]() $p-i^*$ is even and that equation
$p-i^*$ is even and that equation  $\sum_{i=0}^{p-i^*} \tilde b_{i+i^*,0} x^{i}=0$ cannot have a real solution (otherwise condition (c2) is not satisfied). Taking this into account, we can write
$\sum_{i=0}^{p-i^*} \tilde b_{i+i^*,0} x^{i}=0$ cannot have a real solution (otherwise condition (c2) is not satisfied). Taking this into account, we can write
 \begin{equation*}
\sum_{i=0}^{p-i^*} \tilde b_{i+i^*,0} x^{i} = \tilde b_{p,0} \prod_{k=1}^{(p-i^*)/2} (x^2 -2 \tilde \alpha_k x + (\tilde \alpha_k^2+\tilde \beta_k^2)), \quad \text{for some $\tilde \alpha_k,\tilde \beta_k \in \mathbb{R}$ with $\tilde \beta_k \ne 0$}.
\end{equation*}
\begin{equation*}
\sum_{i=0}^{p-i^*} \tilde b_{i+i^*,0} x^{i} = \tilde b_{p,0} \prod_{k=1}^{(p-i^*)/2} (x^2 -2 \tilde \alpha_k x + (\tilde \alpha_k^2+\tilde \beta_k^2)), \quad \text{for some $\tilde \alpha_k,\tilde \beta_k \in \mathbb{R}$ with $\tilde \beta_k \ne 0$}.
\end{equation*} In this case, the origin of system (6) is the unique equilibrium point of system (6) and taking  $\tilde b_{i^*,0} \lt 0$ and A < 0, all conditions (c1)–(c3) are satisfied. Note that
$\tilde b_{i^*,0} \lt 0$ and A < 0, all conditions (c1)–(c3) are satisfied. Note that
 \begin{equation*}
\tilde b_{i^*,0}= \tilde b_{p,0} \prod_{k=1}^{(p-i^*)/2} (\alpha_k^2 +\beta_k^2),
\end{equation*}
\begin{equation*}
\tilde b_{i^*,0}= \tilde b_{p,0} \prod_{k=1}^{(p-i^*)/2} (\alpha_k^2 +\beta_k^2),
\end{equation*}and since  $\tilde b_{i^*,0} \lt 0$, this implies that
$\tilde b_{i^*,0} \lt 0$, this implies that  $\tilde b_{p,0} \lt 0$.
$\tilde b_{p,0} \lt 0$.
We recall that p is odd, m is even and ![]() $b_{p,0} \lt 0$. A study (see [Reference Dumortier and Herssens6]) of such system in a neighbourhood of the origin on the Poincaré sphere forms the backbone of the proof. In this case system, (6) is a generalized Liénard differential system with p odd, m even,
$b_{p,0} \lt 0$. A study (see [Reference Dumortier and Herssens6]) of such system in a neighbourhood of the origin on the Poincaré sphere forms the backbone of the proof. In this case system, (6) is a generalized Liénard differential system with p odd, m even, ![]() $p \gt m+1$ and
$p \gt m+1$ and  $\tilde b_{p,0} \lt 0$. We can indeed make the rescaling
$\tilde b_{p,0} \lt 0$. We can indeed make the rescaling
 \begin{equation*}
x =\alpha X, \quad y = \beta Y, \quad t =\gamma s, \quad \alpha=\left(\frac{b_{m,1}^2}{\tilde b_{p,0}} \right)^{1/(p-1-2m)}, \quad \gamma =-\frac{1}{b_{m,1} \alpha^m}, \quad \beta=\frac{\alpha}{\gamma},
\end{equation*}
\begin{equation*}
x =\alpha X, \quad y = \beta Y, \quad t =\gamma s, \quad \alpha=\left(\frac{b_{m,1}^2}{\tilde b_{p,0}} \right)^{1/(p-1-2m)}, \quad \gamma =-\frac{1}{b_{m,1} \alpha^m}, \quad \beta=\frac{\alpha}{\gamma},
\end{equation*}and system (6) becomes
 \begin{equation}
X^{\prime} =Y, \qquad Y^{\prime} =A Y + X^{i^*} \sum_{i=0}^{p-i^*-1} \hat b_{i+i^*,0} X^{i} - X^p + Y
\left(\hat b_{m,1} \prod_{i=1}^{m/2} \left((X-\hat \alpha_i)^2 + \hat \beta_i^2\right)-A \right),
\end{equation}
\begin{equation}
X^{\prime} =Y, \qquad Y^{\prime} =A Y + X^{i^*} \sum_{i=0}^{p-i^*-1} \hat b_{i+i^*,0} X^{i} - X^p + Y
\left(\hat b_{m,1} \prod_{i=1}^{m/2} \left((X-\hat \alpha_i)^2 + \hat \beta_i^2\right)-A \right),
\end{equation}where  $\hat b_{2i,1}$,
$\hat b_{2i,1}$,  $\hat b_{m,1}$,
$\hat b_{m,1}$, ![]() $\hat \alpha_i$ and
$\hat \alpha_i$ and ![]() $\hat \beta_i$ are the new parameters, and the coefficient of
$\hat \beta_i$ are the new parameters, and the coefficient of ![]() $Y X^m$ is −1.
$Y X^m$ is −1.
Note that now system (9) is a generalized Liénard differential system with p odd, m even, and the coefficient of Xp equal to −1. Using the differential system (3) of [Reference Dumortier and Herssens6] with ɛ = 1, m odd and n even (in the notation of [Reference Dumortier and Herssens6]), we get that the infinity of system (9) must be one of the following five infinities described in the phase portraits of Figure 5(3), Figure 6(1), Figure 7(3), Figure 8(6) and Figure 9(3).
From these previous figures, we get that either the infinity is a repeller (there are orbits which come from infinity, but there are no orbits going to infinity) in Figure 5(3), Figure 6(1) and Figure 7(3) or there are no orbits going or coming from infinity in Figure 8(6) and Figure 9(3).
Note that since the divergence of the system is negative (condition (c1)), thanks to Poincaré-Bendixson Theorem (see for instance [Reference Dumortier, Llibre and Artés7, Theorem 7.10]), no periodic orbit exist and conditions (c1)–(c3) together with the behaviour at infinity previously described imply that the origin is globally asymptotically stable. This concludes the proof of Theorem 1.
Funding Statement
The first author is partially supported by the Agencia Estatal de Investigación grant no. PID2019-104658GB-I00, the H2020 European Research Council grant no. MSCA-RISE-2017-777911, AGAUR (Generalitat de Catalunya) grant no. 2022-SGR 00113, and the Acadèmia de Ciències i Arts de Barcelona. The second author is partially supported by FCT/Portugal through CAMGSD, IST-ID, projects UIDB/04459/2020 and UIDP/04459/2020.
Competing Interests
The authors have no competing interests.