Hostname: page-component-77c89778f8-rkxrd Total loading time: 0 Render date: 2024-07-21T15:17:50.535Z Has data issue: false hasContentIssue false
  • English
  • Français

18.—Asymptotic Estimates for the Lengths of the Gaps in the Essential Spectrum of Self-adjoint Differential Operators

Published online by Cambridge University Press:  14 February 2012

M. S. P. Eastham  and
W. N. Everitt
M. S. P. Eastham
Affiliation:
Chelsea College, University of London
Get access Rights & Permissions [Opens in a new window]

Synopsis

The paper gives asymptotic estimates of the form

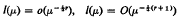
as λ→∞ for the length l(μ)of a gap, centre μ in the essential spectrum associated with second-order singular differential operators. The integer r will be shown to depend on the differentiability properties of the coefficients in the operators and, in fact, r increases with the increasing differentiability of the coefficients. The results extend to all r ≧ – 2 the long-standing ones of Hartman and Putnam [10], who dealt with r = 0, 1, 2.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 74 , 1976 , pp. 239 - 252
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References

1Borg, G.. Eine Umkerhrung der Sturm-Liouvilleschen Eigenwertaufgabe. Acta. Math. 78 (1946), 1–96.CrossRefGoogle Scholar
2Dunford, N. and Schwartz, J. T.. Linear operators, II (New York: Interscience, 1963).Google Scholar
3Eastham, M. S. P.. Conditions for the spectrum in eigenfunction theory to consist of (— ∞, ∞). Quart. J. Math. Oxford Ser. 18 (1967), 147–154.CrossRefGoogle Scholar
4Eastham, M. S. P.. Gaps in the essential spectrum associated with singular differential operators. Quart. J. Math. Oxford Ser. 18 (1967), 155–168.Google Scholar
5Eastham, M. S. P.. On the gaps in the spectrum associated with Hill's equation. Proc. Amer. Math. Soc. 21 (1969), 643–647.Google Scholar
6Eastham, M. S. P.. The spectral theory of periodic differential equations (Edinburgh: Scottish Academic Press, 1973).Google Scholar
7Eastham, M. S. P.. Results and problems in the spectral theory of periodic differential equations. Proceedings of the Dundee symposium on spectral theory and differential equations. Lecture Notes in Math. 448 (Berlin: Springer, 1975).Google Scholar
8Eastham, M. S. P. and El-Deberky, A. A.. The spectrum of differential operators with large coefficients. J. London Math. Soc. 2 (1970), 257–266.CrossRefGoogle Scholar
9Glazman, I. M.. Direct methods of qualitative spectral analysis of singular differential operators (Jerusalem: I.P.S.T., 1965).Google Scholar
10Hartman, P. and Putnam, C. R.. The gaps in the essential spectra of wave equations. Amer. J.Math. 72 (1950), 849–862.CrossRefGoogle Scholar
11Hochstadt, H.. A special Hill's equation with discontinuous coefficients. Amer. Math. Monthly 70 (1963), 18–26.CrossRefGoogle Scholar
12Hochstadt, H.. Estimates on the instability intervals for Hill's equation. Proc. Amer. Math. Soc. 14 (1963), 930–932.Google Scholar
13Lee, J. W.. Spectral properties and oscillation theorems for periodic boundary-value problems of Sturm-Liouville type. J. Differential Equations 11 (1972), 592–606.CrossRefGoogle Scholar
14Lee, J. W.. Interlacing of eigenvalues for periodic and odd-periodic boundary-value problems. J. Differential Equations 16 (1974), 394–398.Google Scholar
15Ntinos, A.. Differential equations: periodic boundary value problems (London Univ. Ph.D. thesis, 1974).Google Scholar
16Simonyan, S. G.. Asymptotic properties of the width of gaps in the spectrum of a Sturm-Liouville operator with a period analytic potential. Differential Equations 6 (1970), 965–971.Google Scholar
17Titchmarsh, E. C.. Theory of functions (2nd edn) (Oxford Univ. Press, 1939).Google Scholar
18Titchmarsh, E. C.. Eigenfunction problems with periodic potentials. Proc. Roy. Soc. London Ser. A. V203 (1950), 501–514.Google Scholar
19Titchmarsh, E. C.. Eigenfunction expansions, II (Oxford Univ. Press, 1958).Google Scholar
20Wintner, A.. Stability and spectrum in the wave mechanics of lattices. Phys. Rev. 11 (1947), 81–82.Google Scholar

Additional reference:

Hartman, P.J . London. Math. Soc. 27 (1952), 492–496. A comment on this reference will be made in a further paper (in preparation) on the higher-order case,Google Scholar