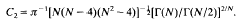Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Grunau, Hans-Christoph
1995.
Positive solutions to semilinear polyharmonic Dirichlet problems involving critical Sobolev exponents.
Calculus of Variations and Partial Differential Equations,
Vol. 3,
Issue. 2,
p.
243.
1997.
Variational Methods for Potential Operator Equations.
p.
270.
Gazzola, Filippo
1998.
Critical growth problems for polyharmonic operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 128,
Issue. 2,
p.
251.
Deng, Yinbin
and
Wang, Gengsheng
1999.
On inhomogeneous biharmonic equations involving critical exponents.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 129,
Issue. 5,
p.
925.
Jannelli, Enrico
and
Lazzo, Monica
1999.
Fundamental solutions and nonlinear elliptic critical problems.
ANNALI DELL UNIVERSITA DI FERRARA,
Vol. 45,
Issue. 1,
p.
155.
Jannelli, Enrico
1999.
The Role Played by Space Dimension in Elliptic Critical Problems.
Journal of Differential Equations,
Vol. 156,
Issue. 2,
p.
407.
Alves, C.O.
Marcos do Ó, João
and
Miyagaki, O.H.
2001.
Nontrivial solutions for a class of semilinear biharmonic problems involving critical exponents.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 46,
Issue. 1,
p.
121.
Chabrowski, J.
and
Marcos do Ó, João
2002.
On some fourth-order semilinear elliptic problems in.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 49,
Issue. 6,
p.
861.
Fernández Bonder, Julián
and
Rossi, Julio D.
2002.
A fourth order elliptic equation with nonlinear boundary conditions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 49,
Issue. 8,
p.
1037.
Alves, C.O.
do Ó, João Marcos
and
Miyagaki, O.H.
2003.
On a class of singular biharmonic problems involving critical exponents.
Journal of Mathematical Analysis and Applications,
Vol. 277,
Issue. 1,
p.
12.
Galaktionov, Victor A.
and
King, John R.
2003.
Composite structure of global unbounded solutions of nonlinear heat equations with critical Sobolev exponents.
Journal of Differential Equations,
Vol. 189,
Issue. 1,
p.
199.
Ebobisse, François
and
Ahmedou, Mohameden Ould
2003.
On a nonlinear fourth-order elliptic equation involving the critical Sobolev exponent.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 52,
Issue. 5,
p.
1535.
Ben Ayed, Mohamed
El Mehdi, Khalil
and
Hammami, Mokhless
2005.
Some existence results for a Paneitz type problem via the theory of critical points at infinity.
Journal de Mathématiques Pures et Appliquées,
Vol. 84,
Issue. 2,
p.
247.
Ge, Yuxin
2005.
Positive solutions in semilinear critical problems for polyharmonic operators.
Journal de Mathématiques Pures et Appliquées,
Vol. 84,
Issue. 2,
p.
199.
Xiong, Hui
and
Shen, Yao Tian
2005.
Nonlinear Biharmonic Equations with Critical Potential.
Acta Mathematica Sinica, English Series,
Vol. 21,
Issue. 6,
p.
1285.
Liu, Yue
and
Wang, Zhengping
2007.
Biharmonic equations with asymptotically linear nonlinearities.
Acta Mathematica Scientia,
Vol. 27,
Issue. 3,
p.
549.
Yang, Min Bo
and
Shen, Zi Fei
2008.
Infinitely many solutions for a class of fourth order elliptic equations in R N.
Acta Mathematica Sinica, English Series,
Vol. 24,
Issue. 8,
p.
1269.
Wang, Youjun
and
Shen, Yaotan
2009.
Multiple and sign-changing solutions for a class of semilinear biharmonic equation.
Journal of Differential Equations,
Vol. 246,
Issue. 8,
p.
3109.
Galaktionov, V A
2009.
Five types of blow-up in a semilinear fourth-order reaction–diffusion equation: an analytic–numerical approach.
Nonlinearity,
Vol. 22,
Issue. 7,
p.
1695.
Ge, Yuxin
Wei, Juncheng
and
Zhou, Feng
2011.
A critical elliptic problem for polyharmonic operators.
Journal of Functional Analysis,
Vol. 260,
Issue. 8,
p.
2247.
 L2N/(N–4) (RN) is attained by all translations and dilations of (1 + ∣x∣2)(4-N)/2. The best constant is found to be
L2N/(N–4) (RN) is attained by all translations and dilations of (1 + ∣x∣2)(4-N)/2. The best constant is found to be